目录
前言
本文其实属于:Python的进阶之道【AIoT阶段一】的一部分内容,本篇把这部分内容单独截取出来,方便大家的观看,本文介绍 NumPy 高级,学习之前需要学习:NumPy入门
1.数据形状改变
1.1 数组变形
🚩我们可以使用 reshape() 方法,把数组任意的进行形状的变化:
import numpy as np
nd2 = np.random.randint(0,100, size =(3,4))
display(nd2)# 数据重塑 reshape# 我们的 nd2 是一个三行四列的数组,我们可以把它变成四行三列
display(nd2.reshape(4,3))# 再来举例,我们把它变成两行六列# 方法一:
display(nd2.reshape(2,6))# 方法二:
display(nd2.reshape(-1,6))# -1 表示的是最后计算:相当于 x * 6 = 3 * 4 ---> x = 2# -1 适合不关心总数的情况,不关心总数是多少,比较灵活
display(nd2.reshape(-1))# 相当于 x = 3 * 4 ---> x = 12

1.2 数组堆叠
🚩我们可以使用 concatenate() 进行数组的合并:
arr1 = np.random.randint(0,10, size =(2,4))
arr2 = np.random.randint(0,10, size =(2,4))
display(arr1, arr2)# 合并,默认进行(xing)行(hang)合并
display(np.concatenate([arr1, arr2]))# 我们还可以合并多个
display(np.concatenate([arr1, arr2, arr1]))

那么我们是否可以合并一个三行四列的数组和一个四行三列的数组呢?
真的没有办法了么?其实不然,我们通过观察这两个数组可以发现,虽然这两个数组的列数不同,但是这两个数组的行数是相同的,故我们可以进行列合并:
arr1 = np.random.randint(0,10, size =(3,5))
arr2 = np.random.randint(0,10, size =(3,4))
display(arr1, arr2)# axis = 0(默认值),代表行# axis = 1表示列,-1也可以表示
display(np.concatenate([arr1, arr2], axis =1))
display(np.concatenate([arr1, arr2], axis =-1))

1.3 数组拆分
🚩使用 split() 函数可以把数组进行拆分:
nd = np.random.randint(0,100, size =(6,9))
display(nd)# 行拆分
display(np.split(nd,2))# 平均拆分为2份
display(np.split(nd,3))# 平均拆分为3份
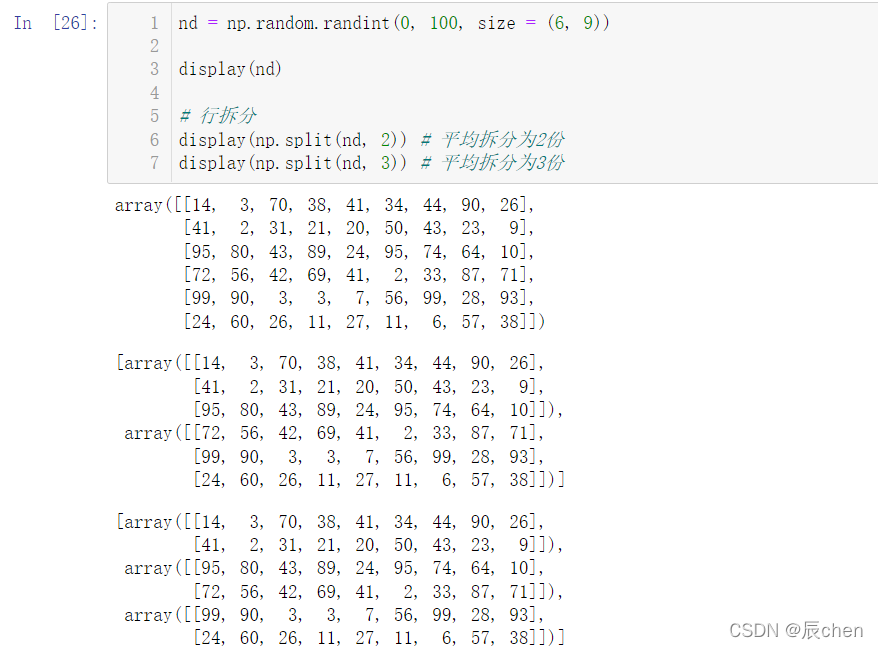
我们还可以不是平均拆分:
nd = np.random.randint(0,100, size =(6,9))
display(nd)# 列表表示按节点进行拆分
np.split(nd,[1,4,5])# 1 切一刀,4 切一刀,5 切一刀# 分成了 [0, 1) [1, 4) [4, 5) [5, 6)

我们不仅可以拆分行,也可以拆分列,还是和 2.1.2 数组堆叠 一样,参数
axis = 0(默认值),代表行
,
axis = 1,代表列
nd = np.random.randint(0,100, size =(6,9))
display(nd)
np.split(nd,3, axis =1)# 平均拆成三分(列拆分)# 列表表示按节点进行拆分
np.split(nd,[1,4,5], axis =1)# 1 切一刀,4 切一刀,5 切一刀# 分成了 [0, 1) [1, 4) [4, 5) [5, 9)

1.4 数组转置
🚩对于数组的转置,我们可以利用 T 进行转置,也可以使用 numpy 中的 transpose() 方法:
A = np.random.randint(0,10, size =(3,5))
display(A)# 所谓转置就是行变列,列边行
display(A.T)# 还可以按照下面的方法进行转置
display(np.transpose(A, axes =[1,0]))

2.广播机制
🚩所谓广播,就是对原本数据的不断复制,复制到和目标数组相同的构造的时候,比如我们有一个三行四列的数组,要加一行四列的数组,那么一行四列的数组就会自己复制三份,变成三行四列的数组,其中每一行都和原本数组的值相同,变成这种形式之后,再和原三行四列的数组进行相加运算,下面,我们从三个方面进行代码演示:一维数组的广播,二维数组的广播,三维数组的广播。
2.1 一维数组的广播
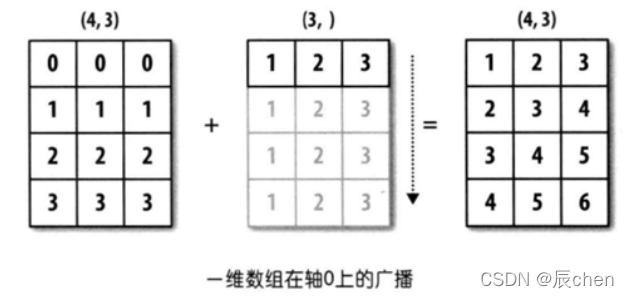
arr1 = np.random.randint(0,10, size =(5,3))
arr2 = np.arange(1,4)
display(arr1, arr2)# arr1 有五行,arr2 只有一行# 它们俩的相加就是通过广播机制# 广播机制:arr2 变身,变成了五份(一模一样)# 每一份对应每一行的相加
arr1 + arr2

2.2 二维数组的广播
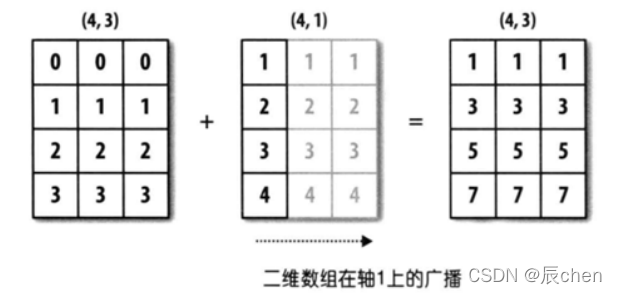
arr3 = np.random.randint(0,10, size =(4,5))# 计算每一行的平均值
arr4 = arr3.mean(axis =1)
display(arr3, arr4)# 注意 arr3 每一行5个数,arr4一行中为4个数
arr3 - arr4 # 形状不匹配,所以报错
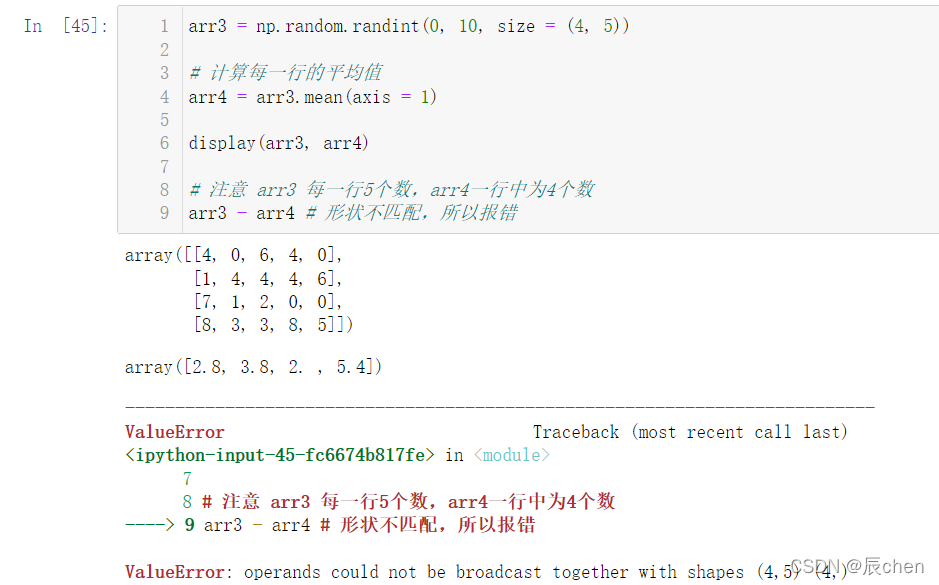
因为形状不匹配的原因,故会报错,我们可以使用 2.1.1 数组变形 中的 reshape() 方法,对数组进行更改:
arr3 = np.random.randint(0,10, size =(4,5))# 计算每一行的平均值
arr4 = arr3.mean(axis =1)
display(arr3, arr4)# 形状改变,arr4改为了四行一列
display(arr4.reshape(4,1))# arr3为四行五列
arr3 - arr4.reshape(4,1)

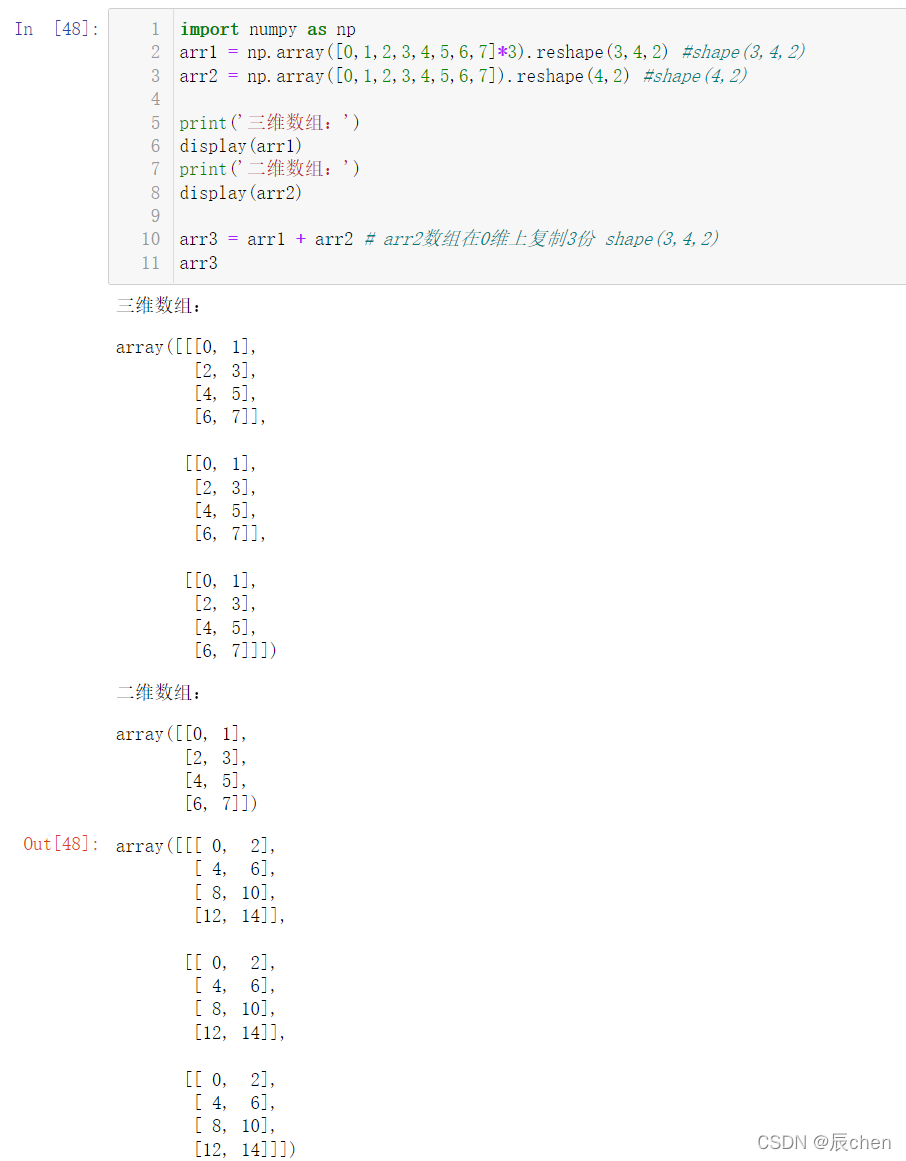
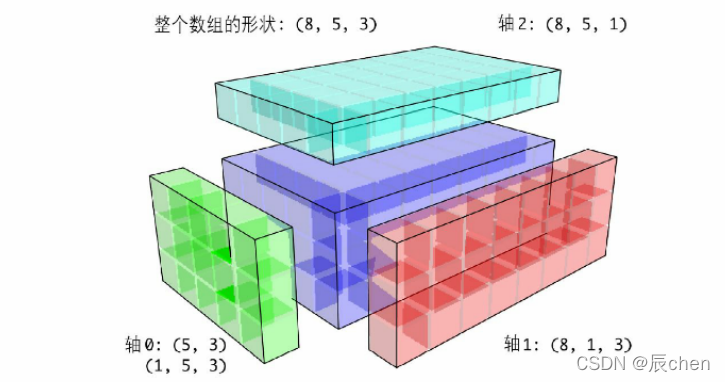
2.3 三维数组的广播
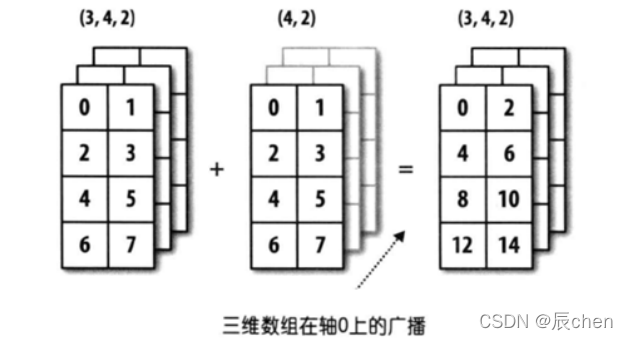
import numpy as np
arr1 = np.array([0,1,2,3,4,5,6,7]*3).reshape(3,4,2)#shape(3,4,2)
arr2 = np.array([0,1,2,3,4,5,6,7]).reshape(4,2)#shape(4,2) print('三维数组:')
display(arr1)print('二维数组:')
display(arr2)
arr3 = arr1 + arr2 # arr2数组在0维上复制3份 shape(3,4,2)
arr3
3.通用函数
3.1 元素级数字函数
🚩NumPy 中和数学相关的函数有很多:abs、sqrt、square、exp、log、sin、cos、tan,maxinmum、minimum、all、any、inner、clip、round、trace、ceil、floor,下面我们挑几个常用的进行代码演示,感兴趣的读者可以自己搜索其他函数的用法并实践,这里不做过多演示:
# 圆周率
display(np.pi)# 计算 sin90°
display(np.sin(90))# 这是不合法的,90是int型,而非度数
display(np.sin(np.pi /2))# pi 是 180°,故 pi / 2 就代表 90°# 计算 cos90°
display(np.cos(np.pi /2))
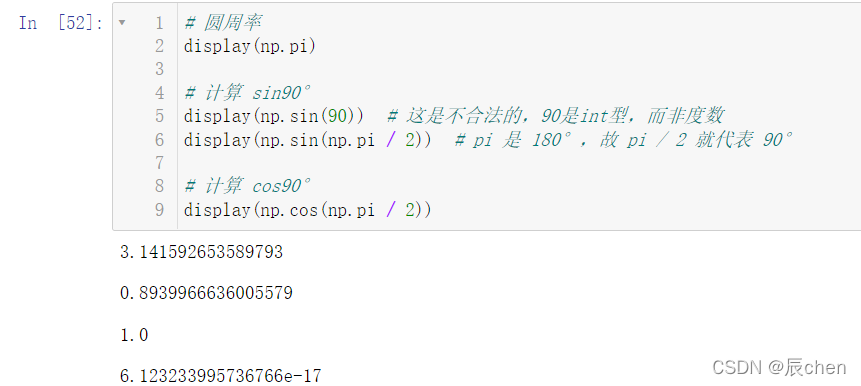
一个很有意思的现象出现了,计算 cos90°的结果并不显示0,而是显示e-7,这是因为我们在计算的过程中会有精度问题,故我们一般表示0即当一个数小于一个很小的数的时候,我们就认为这个数为0,我们可以使用 round(n) 函数让它保留n位小数:
# 保留一位小数:
display(np.cos(np.pi /2).round(1))# 保留五位小数:
display(np.cos(np.pi /2).round(5))

可以看到,就算我们保留五位小数,依旧是0,故我们认为这个数是0
# 开平方
display(np.sqrt(1024))# 平方
display(np.square(8))# 幂运算
display(np.power(2,3))# 计算2的3次方# log运算
display(np.log2(16))# 计算log以2为底16的对数

# 依次比较两个等长数组,返回对应位置元素的最大值
x = np.array([6,6,0,7,2,5])
y = np.array([9,5,6,3,4,2])
display(np.maximum(x, y))# 依次比较两个等长数组,返回对应位置元素的最小值
x = np.array([6,6,0,7,2,5])
y = np.array([9,5,6,3,4,2])
display(np.minimum(x, y))

# 返回一维数组向量内积
arr = np.random.randint(0,10, size =(2,2))
display(arr)
np.inner(arr[0], arr)

a =6.66666# 向上取整
display(np.ceil(a))# 向下取整
display(np.floor(a))

# 裁剪,小于就拔高,大于就降低
arr = np.random.randint(0,30, size =20)
display(arr)# 10:小于10:变成10;# 20:大于20:变成20
np.clip(arr,10,20)

3.2 where函数
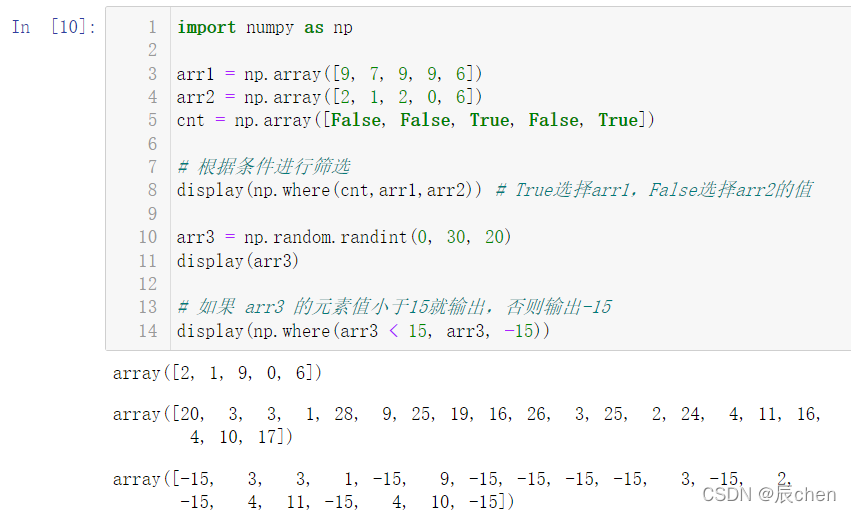
import numpy as np
arr1 = np.array([9,7,9,9,6])
arr2 = np.array([2,1,2,0,6])
cnt = np.array([False,False,True,False,True])# 根据条件进行筛选
display(np.where(cnt,arr1,arr2))# True选择arr1,False选择arr2的值
arr3 = np.random.randint(0,30,20)
display(arr3)# 如果 arr3 的元素值小于15就输出,否则输出-15
display(np.where(arr3 <15, arr3,-15))
3.3排序方法
🚩NumPy中还提供了排序方法,排序方法是就地排序,即直接改变原数组:
arr.sort()、np.sort()、arr.argsort()
import numpy as np
arr = np.array([14,9,13,13,18,18,18,7,5,11])# 直接让原数组从小到大进行排序
arr.sort()
display(arr)# 返回深拷贝排序结果
np.sort(arr)
arr = np.array([14,9,13,13,18,18,18,7,5,11])
display(arr)# 返回从小到大排序的索引
display(arr.argsort())

3.4 集合运算函数
A = np.array([6,8,9,1,4])
B = np.array([3,6,5,7,1])# 计算交集
display(np.intersect1d(A, B))# 计算并集
display(np.union1d(A, B))# 计算差集
display(np.setdiff1d(A, B))

3.5数学和统计函数
🚩我们挑几个常用的函数进行代码演示,剩余的函数有兴趣的读者可以自行查阅用法自己演示。min、max、mean、median、sum、std、var、cumsum、cumprod、argmin、argmax、argwhere、cov、corrcoef
import numpy as np
arr1 = np.array([5,90,87,35,23,6,39,39,99,79,72,94,97,13,84])# 计算数组中的最小值
display(arr1.min())# 计算数组中的最大值的索引
display(arr1.argmax())# 返回大于40的元素的索引
display(np.argwhere(arr1 >40))# 计算数组的累加和
display(np.cumsum(arr1))
arr2 = np.random.randint(0,10,size =(4,5))
display(arr2)# 计算列的平均值
display(arr2.mean(axis =0))# 计算行的平均值
display(arr2.mean(axis =1))# 协方差矩阵
display(np.cov(arr2, rowvar =True))# 相关性系数
display(np.corrcoef(arr2, rowvar =True))

4.矩阵运算
4.1 矩阵的乘法
#矩阵的乘积(点乘)
A = np.array([[2,1,7],[6,3,4]])# shape(2, 3)
B = np.array([[4,3],[0,9],[-5,-8]])# shape(3, 2) # 第一种方法
display(np.dot(A,B))# 第二种方法
display(A @ B)# 符号 @ 表示矩阵乘积运算# 第三种方法
display(A.dot(B))
4.2 矩阵的其他运算
np.set_printoptions(suppress =True)# 不使用科学计数法from numpy.linalg import inv,det,eig,qr,svd
A = np.array([[1,2,3],[2,3,1],[3,2,1]])# shape(3, 3) # 求逆矩阵
B = inv(A)# B 就是 A 的逆矩阵
display(B)
display(A.dot(B))# 求矩阵的行列式
display(det(A))

5.训练场
5.1 给定一个4维矩阵,如何得到最后两维的和?(提示,指定axis进行计算)
import numpy as np
arr = np.random.randint(0,10, size =(2,3,4,5))
display(arr)
display(arr.sum(axis =0))# 第0维的数据进行加和
display(arr.sum(axis =1))# 第1维的数据进行加和
display(arr.sum(axis =-1))# 最后一维的数据进行加和# 最后两维的和# 写法一:
display(arr.sum(axis =(-1,-2)))# 写法二:
display(arr.sum(axis =(2,3)))

5.2 给定数组[1, 2, 3, 4, 5],如何得到在这个数组的每个元素之间插入3个0后的新数组?
import numpy as np
arr1 = np.arange(1,6)
display(arr1)# 每个元素之间插入3个0,共插入3*4=12个0# 再加上初始的5个值,共需要17个位置# 创建一个长度为17的全部是0的数组
arr2 = np.zeros(shape =17, dtype = np.int16)
display(arr2)# 有间隔的,每4个取一个,取出数据并进行替换
arr2[::4]= arr1
display(arr2)

5.3 给定一个二维矩阵(5行4列),如何交换其中两行的元素(提示:任意调整,花式索引)?
import numpy as np
arr = np.random.randint(0,100, size =(5,4))
display(arr)# 使用花式索引进行交换
arr = arr[[0,2,1,3,4]]
display(arr)

5.4 创建一个100000长度的随机数组,使用两种方法对其求三次方(1、for循环;2、NumPy自带方法),并比较所用时间
%%time
:可以显示代码的运行时间,这个执行时间会和电脑的性能挂钩
使用 for 循环
%%time
import numpy as np
arr = np.random.randint(0,10, size =100000)
res =[]for item in arr:
res.append(item **3)
使用NumPy自带方法
%%time
import numpy as np
arr = np.random.randint(0,10, size =100000)
res =[]
arr2 = np.power(arr,3)
可以发现,使用 NumPy 自带方法运行效率要远远高于使用 for 循环
5.5 创建一个5行3列随机矩阵和一个3行2列随机矩阵,求矩阵积
import numpy as np
A = np.random.randint(0,10, size =(5,3))
B = np.random.randint(0,10, size =(3,2))
display(A, B)# 调用 NumPy 函数 dotprint('方式一:\n', np.dot(A, B))# 调用对象方法print('方式二:\n', A.dot(B))# 使用符号计算print('方式三:\n', A @ B)
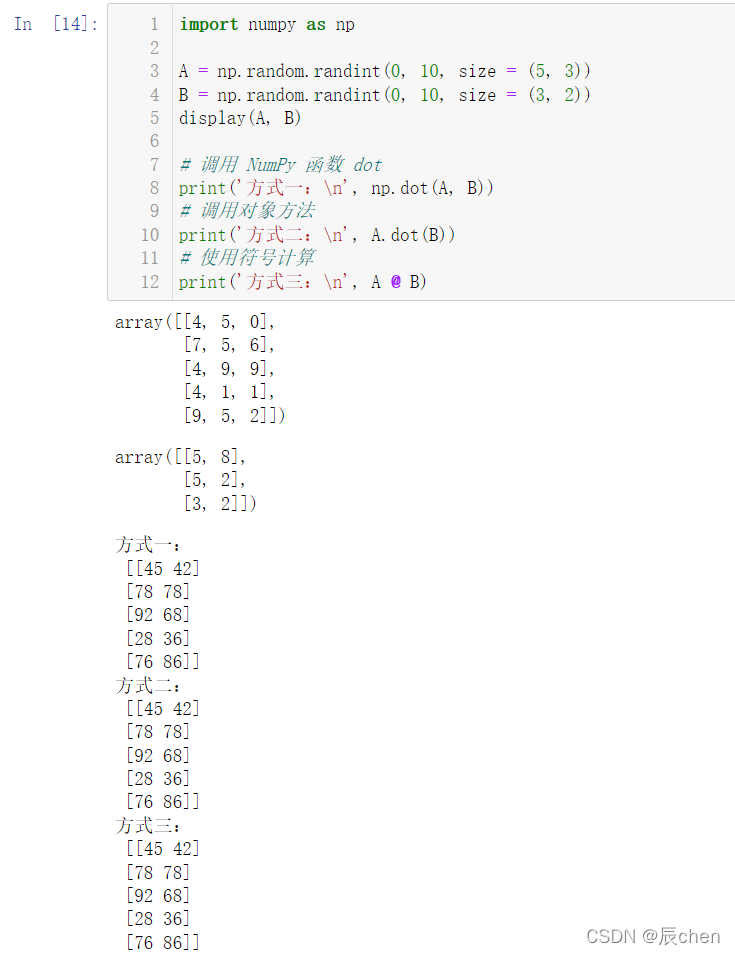
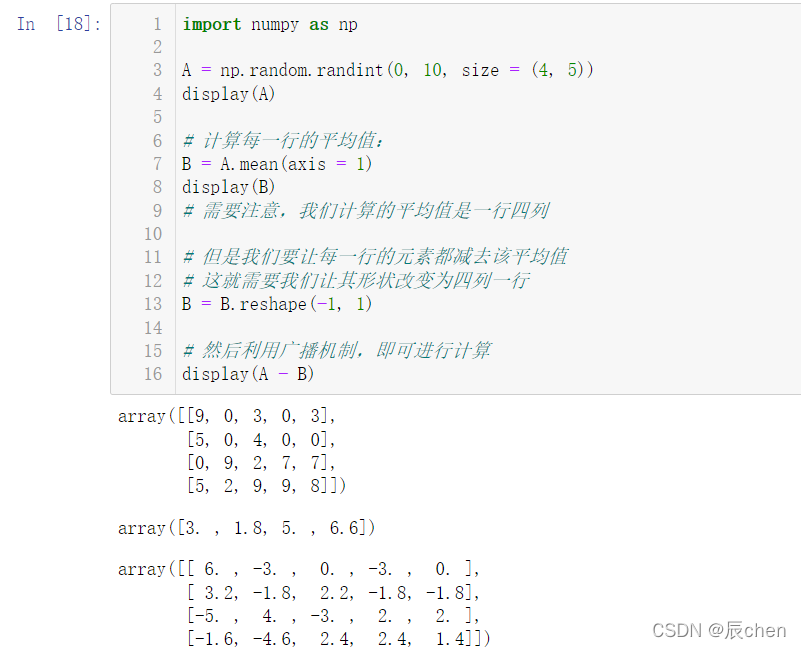
5.6 矩阵的每一行的元素都减去该行的平均值(注意,平均值计算时指定axis,以及减法操作时形状改变)
import numpy as np
A = np.random.randint(0,10, size =(4,5))
display(A)# 计算每一行的平均值:
B = A.mean(axis =1)
display(B)# 需要注意,我们计算的平均值是一行四列# 但是我们要让每一行的元素都减去该平均值# 这就需要我们让其形状改变为四列一行
B = B.reshape(-1,1)# 然后利用广播机制,即可进行计算
display(A - B)
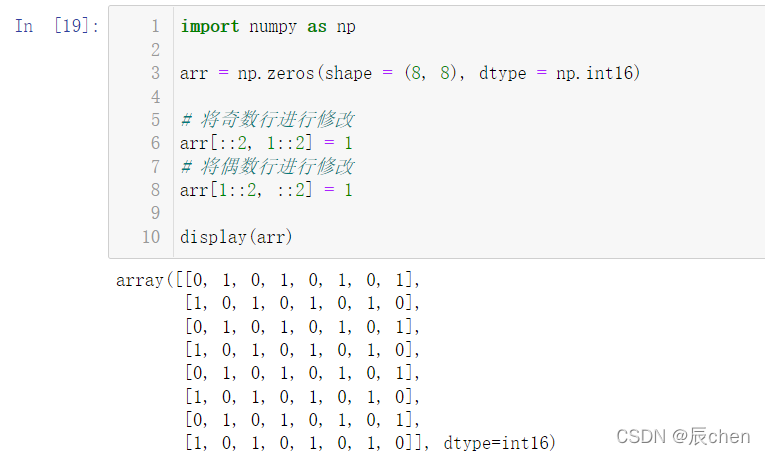
5.7 打印出以下函数(要求使用np.zeros创建8*8的矩阵):
[[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]
[0 1 0 1 0 1 0 1]
[1 0 1 0 1 0 1 0]]
import numpy as np
arr = np.zeros(shape =(8,8), dtype = np.int16)# 将奇数行进行修改
arr[::2,1::2]=1# 将偶数行进行修改
arr[1::2,::2]=1
display(arr)
5.8 正则化一个5行5列的随机矩阵(数据统一变成0~1之间的数字,相当于进行缩小)
正则的概念:矩阵A中的每一列减去这一列最小值,除以每一列的最大值减去每一列的最小值(提示:
轴axis给合适的参数!!!)
A
=
A
−
A
.
m
i
n
A
.
m
a
x
−
A
.
m
i
n
\rm{A = \frac{A - A.min}{A.max - A.min}}
A=A.max−A.minA−A.min
import numpy as np
A = np.random.randint(1,10, size =(5,5))
display(A)# axis = 1 代表行
display(A.min(axis =1))# axis = 0 代表列
display(A.min(axis =0))# 根据公式计算
B =(A - A.min(axis =0))/(A.max(axis =0)- A.min(axis =0))
display(B)

5.9 如何根据两个或多个条件过滤numpy数组。加载鸢尾花数据,根据第一列小于5.0并且第三列大于1.5作为条件,进行数据筛选。(提示,需要使用逻辑与运算:&)
我们的数据:
链接:https://pan.baidu.com/s/1VaPHJa6YttfnedO0ewDRtQ
提取码:5u92
我们在下载好数据之后,把它移入到我们如下文件夹中:(直接下载到桌面后,找到该文件夹的位置,然后拖进去即可)
首先我们来介绍一下
.csv
文件,它其实就是一个文本文件,我们打开它(默认打开路径为Excel)
我们也可以选择打开方式为记事本方式:
通过观察不难看出,数据之间通过
,
相隔
接下来介绍一个新方法:
loadtxt()
,其作用为加载数据,比如:
np.loadtxt('./iris.csv', delimiter = ',')
,其作用为打开路径
'./iris.csv'
的文件,这些数据直接通过
,
进行分隔。
import numpy as np
# 加载了文本文件,储存数据都是结构化数据
iris = np.loadtxt('./iris.csv', delimiter =',')
display(iris)
可以看出,这些数据是以二维数组的形式展开的,每一维都有四个数据,分别代表:花萼长度,花萼宽度,花瓣长度,花瓣宽度
import numpy as np
# 加载了文本文件,储存数据都是结构化数据# 花萼长度、花萼宽度、花瓣长度、花瓣宽度
iris = np.loadtxt('./iris.csv', delimiter =',')# 第一列小于5.0
cnt1 = iris[:,0]<5# 第三列大于1.5
cnt2 = iris[:,2]>1.5# 逻辑与运算
cnt = cnt1 & cnt2
display(iris[cnt])

5.10 计算鸢尾花数据每一行的softmax得分(exp表示自然底数e的幂运算)

import numpy as np
iris = np.loadtxt('./iris.csv', delimiter =',')defsoftmax(x):
exp = np.exp(x)# 每一行求和,并且进行形状改变(变成二维,可进行广播)# axis = 1 表示计算每一行的和
res = exp / exp.sum(axis =1).reshape(-1,1)return res.round(3)# 保留3位小数
res = softmax(iris)
display(res)
版权归原作者 辰chen 所有, 如有侵权,请联系我们删除。