【机器学习】
前言
正规方程法(最小二乘)与梯度下降法都是为了求解线性回归的最优参数,但是不同的是正规方程法只需要一步就可以得到代价函数最优点,而梯度下降则是迭代下降,看起来似乎正规方程法要好得多,但实际梯度下降使用场景更多,下面我们介绍这两种算法以及优缺点
梯度下降
一个参数
- 我们从最简单的线性方程解释,后面推广到的多个参数的方程
典型的房价预测问题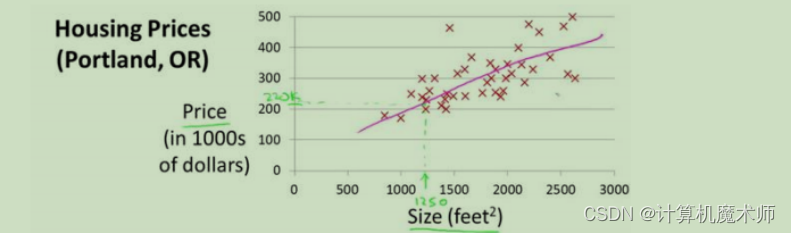
我们假设其数据模型为线性回归模型,方程如下
h θ ( x ) h_\theta(x) hθ(x) = θ 1 ∗ x \theta_1*x θ1∗x我们希望能求出
θ 1 \theta_1 θ1参数,让方程 h θ ( x ) h_\theta(x) hθ(x) 更加拟合数据,梯度下降的方法就是通过求**代价函数**最小得到最优参数或者局部最优参数的,
代价函数
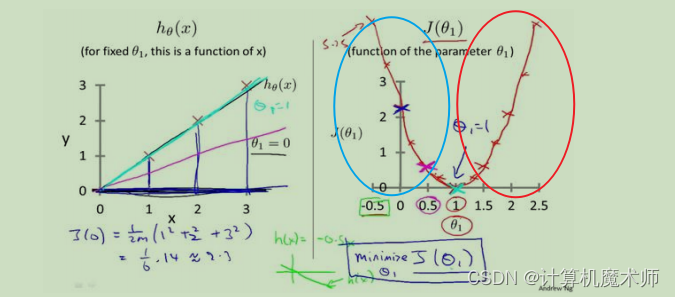
代价函数就是实际数据与数学模型(这里是一元一次方程)所预测的差值,如: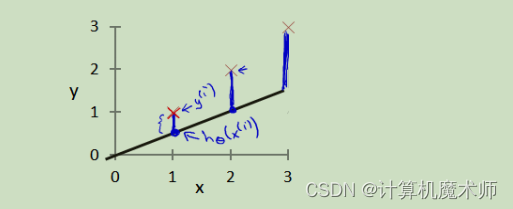
蓝线的长度就是代价函数,可以看到代价函数越大拟合效果越差,代价函数越小,拟合效果越好。
其中关于 **所求方程
h
θ
(
x
)
h_\theta(x)
hθ(x)**(左图)和
θ
1
\theta_1
θ1 的的**代价函数**
h
(
θ
1
)
h(\theta_1)
h(θ1)(右图)如下图:
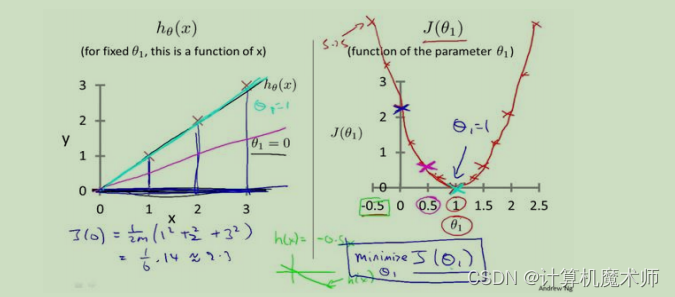
可以看到当方程越拟合数据,代价函数越小,当代价函数
J
(
θ
1
)
J(\theta_1)
J(θ1)值为0时,回归方程
h
θ
(
x
)
h_\theta(x)
hθ(x)完全拟合数据,此时我们要做的就是让代价函数变小。
(后面所讲的正规方程解法就是直接令代价函数为0,求解
θ
\theta
θ参数的)
梯度下降核心方程
迭代求解方程
θ 1 \theta_1 θ1 = θ 1 \theta_1 θ1 - α ∗ δ J ( θ 1 ) δ θ 1 \alpha*\frac{δJ(\theta_1)}{δ\theta_1} α∗δθ1δJ(θ1)
其中
α
\alpha
α是**学习率**,
δ
J
(
θ
0
)
δ
θ
0
\frac{δJ(\theta_0)}{δ\theta_0}
δθ0δJ(θ0) 是对**代价函数**
J
(
θ
1
)
J(\theta_1)
J(θ1)求关于
θ
1
\theta_1
θ1 的偏导数,由于只有一个参数(一阶),所以这里的方程
δ
J
(
θ
1
)
δ
θ
1
\frac{δJ(\theta_1)}{δ\theta_1}
δθ1δJ(θ1) 也可以表示为
d
J
(
θ
1
)
d
θ
1
\frac{dJ(\theta_1)}{d\theta_1}
dθ1dJ(θ1) (即求导数)。
原理讲解
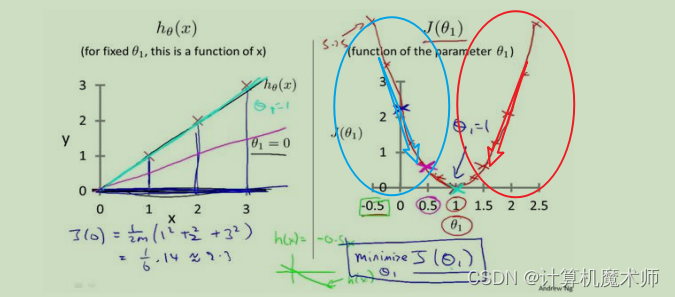
- 当 θ 1 \theta_1 θ1 所在的代价函数区间是单调递增的,如下图(红线标记), 此时 d J ( θ 1 ) d θ 1 \frac{dJ(\theta_1)}{d\theta_1} dθ1dJ(θ1) (即 h θ ( x ) h_\theta(x) hθ(x)的斜率)大于0,则 θ 1 \theta_1 θ1 = θ 1 \theta_1 θ1 - α ∗ δ J ( θ 1 ) δ θ 1 \alpha*\frac{δJ(\theta_1)}{δ\theta_1} α∗δθ1δJ(θ1) 为 θ 1 \theta_1 θ1 减去一个正数, θ 1 \theta_1 θ1往左边退(向代价函数最小值靠近),
- 当 θ 1 \theta_1 θ1 所在的代价函数区间是单调递减时的如图(蓝线标记),此时 θ 1 \theta_1 θ1 = θ 1 \theta_1 θ1 - α ∗ δ J ( θ 1 ) δ θ 1 \alpha*\frac{δJ(\theta_1)}{δ\theta_1} α∗δθ1δJ(θ1) 为 θ 1 \theta_1 θ1 减去一个负数, θ 1 \theta_1 θ1往右边退(向代价函数最小值靠近)
学习率
α
\alpha
α
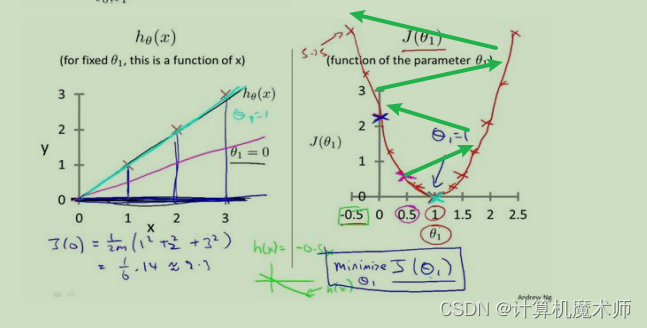
有时我们的迭代方程下降时,可能很缓慢,
需要走很多步(化很久时间)才能到达局部最优或者全局最优 如下图: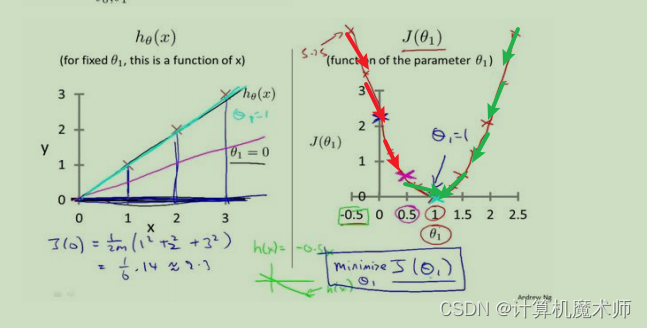
此时学习率
α
\alpha
α的作用就是调整步子长度,让其更快的下降到局部最优或者全局最优
注意:
α \alpha α需要根据数据调节,
- 设置大了,走一步太大了跳到对面那一头了,与想要的结果违背,如图
- 设置小了,步子又太小,所以设置 α \alpha α也是一个细活
两个参数
两个参数
θ
1
\theta_1
θ1,
θ
0
\theta_0
θ0,方程为
h θ ( x ) h_\theta(x) hθ(x) = θ 0 + \theta_0 + θ0+ θ 1 ∗ x \theta_1*x θ1∗x
迭代求解方程
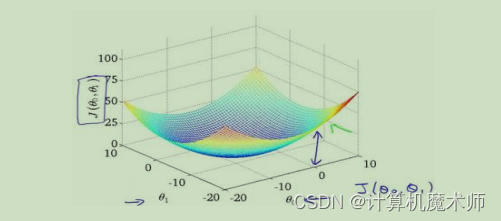
θ 0 \theta_0 θ0 = θ 0 \theta_0 θ0 - α ∗ δ J ( θ 0 ) δ θ 0 \alpha*\frac{δJ(\theta_0)}{δ\theta_0} α∗δθ0δJ(θ0) θ 1 \theta_1 θ1 = θ 1 \theta_1 θ1 - α ∗ δ J ( θ 1 ) δ θ 1 \alpha*\frac{δJ(\theta_1)}{δ\theta_1} α∗δθ1δJ(θ1)此时的代价函数为
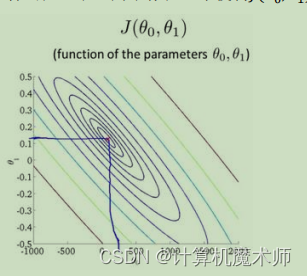
J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1),如下图(是一个碗状,与一个参数的图像一样都是凹函数)
为了更好理解,我们可以绘制出其的等高线
则目标所求的既是 等高线中心 或 碗底,即让代价函数最小
多个参数
在问题案例中,往往有个参数
θ
i
(
i
=
1
,
2
,
3...
)
\theta_i(i=1,2,3...)
θi(i=1,2,3...)
此时的代价方程则时关于多个
θ i \theta_i θi参数,如图
迭代求解方程
θ 0 \theta_0 θ0 = θ 0 \theta_0 θ0 - α ∗ δ J ( θ 0 ) δ θ 0 \alpha*\frac{δJ(\theta_0)}{δ\theta_0} α∗δθ0δJ(θ0) θ 1 \theta_1 θ1 = θ 1 \theta_1 θ1 - α ∗ δ J ( θ 1 ) δ θ 1 \alpha*\frac{δJ(\theta_1)}{δ\theta_1} α∗δθ1δJ(θ1) θ 2 \theta_2 θ2 = θ 2 \theta_2 θ2 - α ∗ δ J ( θ 2 ) δ θ 2 \alpha*\frac{δJ(\theta_2)}{δ\theta_2} α∗δθ2δJ(θ2)…
θ n \theta_n θn = θ n \theta_n θn - α ∗ δ J ( θ n ) δ θ n \alpha*\frac{δJ(\theta_n)}{δ\theta_n} α∗δθnδJ(θn)
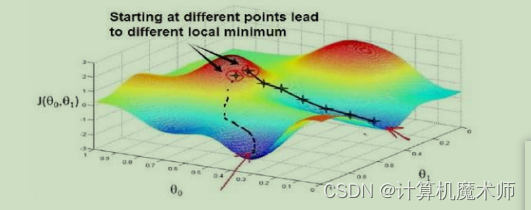
从中也可以看到在梯度下降迭代中,有两个最优结果(其他案例可能有许多),
整个迭代过程可以形象的理解为 你现在在山顶,要找一条最快的路下山,山底就是你的目标地点,也就是代价函数最小
数据标准化
梯度下降在量化纲位不同,如果数
据范围分别是是【0~1000,0 ~5】或者【-0.00004 ~ 0.00002,10 ~ 30】, 那么在使用梯度下降算法时,他们的等高线是一个又窄又高的等高线,如下图: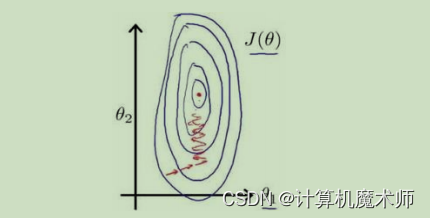
在梯度下降算法中,参数更新就会如上图左右震荡,收敛缓慢,我们就需要对特征进行特征缩放—数据标准化
详解见文章
【机器学习】梯度下降之数据标准化
正规解法
对正规解法来说,一般例子是对代价函数
J
(
θ
)
J(θ)
J(θ)求偏导数,令其为 0 便可以直接算出 最优参数
θ
θ
θ,但大多数情况下
θ
θ
θ是一个多维向量(即有多个参数
θ
i
(
i
=
1
,
2
,
3...
)
\theta_i(i=1,2,3...)
θi(i=1,2,3...)),此时代价函数
f
(
θ
)
f(θ)
f(θ)是关于
θ
θ
θ多维向量的函数,那么要求从
θ
0
θ_0
θ0 到
θ
n
θ_n
θn的值,就分别对对应的
θ
i
θ_i
θi(i = 1,2,3,4…)求偏导数,并令其为0求其最优参数.
假设有M个数据,每个数据N个特征
方程如下:
θ = ( x T ∗ x ) − 1 ∗ x T ∗ y θ = (x^T * x )^{-1} * x^T * y θ=(xT∗x)−1∗xT∗y
这里的
x
x
x为矩阵,该矩阵每一行为
x
i
(
i
=
1
,
2
,
3...
)
x_i(i=1,2,3...)
xi(i=1,2,3...)(
x
i
x_i
xi为列向量,维度为特征N)的向量转置组成,即任意一行的每一列为
x
i
x_i
xi其特征
x
x
x矩阵同下图A矩阵:

这里的
a
11
a_{11}
a11代表第一个数据
x
1
x_1
x1的第一个特征值,依次往下,化简即为

第一行即为
x
1
x_1
x1N维向量的的转置
方程原理讲解视频:
【线性回归】正规方程(最小二乘法)】
由于正规方程是直接求解,所以不需要迭代熟练,不需要“下山",所以不需要对其进行特征缩放(如梯度下降需要数据标准化)
使用场景和优缺点
假设我们有M个数据集,N个特征
梯度下降缺点: 首先需要先提前设定好学习率,并调试,这无疑是额外的工作 需要尝试不同的学习率 ,> 梯度下降缺点:需要多次迭代下降,计算可能会更慢> x
正规解法缺点:在对于大量的数据来说,梯度学习也可以很好的运行结果,而正规方程求解中 > > > > > (> > > > x> > > T> > > > ∗> > > x> > > > )> > > > −> > > 1> > > > > > (x^T * x )^{-1}> > > (xT∗x)−1 这一步中,其维度即为x的特征维度,由于计算机在计算矩阵的逆 的时间复杂度时> > > > > O> > > (> > > > n> > > 3> > > > )> > > > O(n^3)> > > O(n3) ,在特征维度非常大时,运行时间很久,
综上所述:
可以看到他们二者适用场景 不同于数据的大小, 那我们怎么定义数据"大"还是"小"呢, 吴恩达老师给出了一个比较好的区间:
N > 10000 => 梯度下降
N < 10000 => 正规解法
但是不是绝对的判断,还需要根据情况而定
正规方程(不可逆性)* 选读
- 方阵中的两个维度之间存在线性变换关系,导致方阵不满秩
- n(特征数量)相较于m(样本数量)过大,导致其产生的齐次方程组Ax=0不只有零解
这些不可逆的矩阵我们称为奇异矩阵,逆矩阵在不存在时,我们所求的逆矩阵为伪逆
实际上我们案例对应的情况有
- 如,房价预测多了一些特征值,而这个特征值和所有特征值有线性相关,即出现上述第一种情况
- 在特征n >= 数据集数量m的情况下,例如 10 个数据 ,每个数据有 100 个特征,那么我们所要求的
θ就是一个101维向量,10个样本太少了,求得的结果偏离真实值,对应上述情况二,这个时候我们可以减去一些特征,或者使用正则化方法()
其实这种不可逆的情况非常少见,所以在平时案例不用特别担心
版权归原作者 计算机魔术师 所有, 如有侵权,请联系我们删除。