经典八大排序

经典八大排序

文章目录

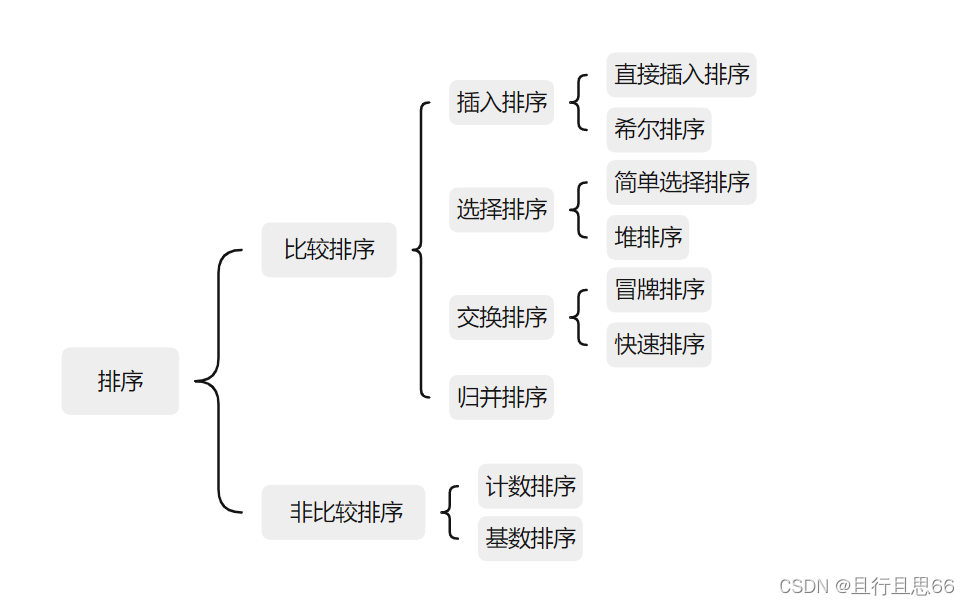
排序的种类：

1.直接插入排序

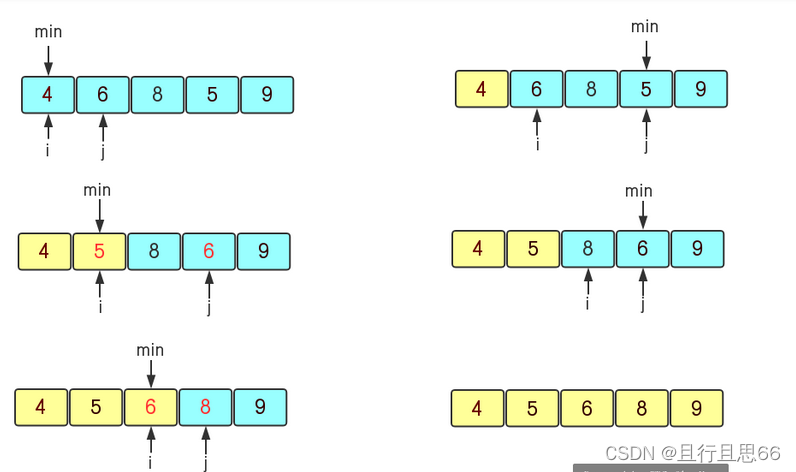
1.该序列第一个元素不用考虑（a1之前不存在子序列），则从第二个元素开始，先把a2的值存在key中，a2>a1则有序不动，a2<a1就把a1往后挪一个，a2放到a1的位置

2.key=a3,a1>a3,a1往后挪，a3挪到a2的位置，a2<a3,位置不变

3.key=a4,a4依次和a1,a3,a2比较，a2,a3,a1依次往后挪，a4放在第一个位置

代码实现：

voidInsertSort(int* a,int len){int begin =1;int i =0;while(begin < len){int key = a[begin];for(i = begin -1; i >=0; i--){if(a[i]<= key)//稳定的{
                a[i +1]= key;break;}
            a[i +1]= a[i];}if(i<0)
            a[0]= key;//说明找完了整个有序子序列都没找到,为最小数
        begin++;}}

算法分析：

• 平均时间复杂度:o(N^2)这是显然的，标准的内外两层循环
• 最好时间复杂度：o(N),如果有序，那么每个元素都已经在在它的待排子序列的合适位置，不用找合适位置
• 最坏时间复杂度:o(N^2)
• 空间复杂度：o(1),因为需要常熟个临时变量
• 稳定性：稳定的

2. 希尔排序

是直接插入排序的优化：

1. 在直接插入排序里，对于一组已经有序的关键字序列进行排序时间复杂度是o(n)，因为每个元素的合适位置的查找都只需一次就能找到，因为左边的有序子序列的最后一个就小于等于该元素，那么就不需要挪动任何元素，每一趟都只用比较一次就结束了单趟排序。 2.放宽第一点的情况，我们不要求有序，其实只要待排序列的有序度越高，也就是逆序对越少，直接插入排序的时间复杂度肯定是越低的（这句话是希尔排序的核心）。具体操作： 先将待排序列分为若干个稀疏的子序列，对这些子序列分别进行直接插入排序。经过这一番调整，整个序列的有序度一定会被提高，逆序对一定会变少。最后，再对整个序列进行一趟直接插入排序。 首先选定子序列中各元素的距离d_i，使待排数据中所有间距为为d_i的数据被分成了一组，在各个组内进行直接插入排序，直到\bg_white \fn_phv d_i=1。此时我们最后一趟进行的就相当于一次完整的（但是效率很高的）直接插入排序。过程： 需要注意的是，虽然每次是对各组进行插入排序，但是写代码时候的思维当然不是直接单独对每个组那样直接插入排序依次，而仍然是从前往后扫描，那么显然，我们每次直接插入排序的key从每次的第一个子序列的第二个元素开始（与直接插入排序同理），然后挨个往后走，每个元素时属于哪个组，我们就把它在其所在组进行直接插入排序，上面的例子中，第一次排序中，我们实际进行时就是从94开始往后走的，第二次排序中，我们就是从05开始的，这样代码就非常好写了。代码：

voidShellSort(int*a,int len){int gap = len;while(gap>1){
        gap = gap /3+1;//先找出增量序列中最大的增量值，分为gap组for(int i = gap; i < len;i++){int key = a[i];int start = i - gap;while(start>=0&&key<=a[start]){
                a[start + gap]= a[start];
                start = start - gap;}
            a[start + gap]= key;}}}

算法分析：

• 平均时间复杂度：o(N1.3)，大量数据研究表明在o(N1.3)附近，事实上也不是严格论证的结果
• 最好时间复杂度：仍然和增量序列的选取有关
• 最坏时间复杂度：o(N^2)
• 空间复杂度：o(1)
• 稳定性：不稳定，例如待排序列（3，2，2，1），取d=2时，显然就能看出是不稳定的

3.简单选择排序

其思想概括来说就是每趟从当前待排序列中选出最小的放在已拍好序列的末尾
指针i 记录待排序列的第一个的元素，指针k用来找待排序列中最小的那个元素，k当然是从i开始，遍历待排序列一趟后，把指针k指向的元素与指针i指向的元素交换，因为待排序列中又少了一个元素，已排序列末尾又多了一个，因此i往后走一个，如此直到待排序列中只剩下一个元素。

代码：

voidSwap(int*a,int a,int b){int tmp = a[a];
    a[a]= a[b];
    a[b]= tmp;}voidSimpleSelectSort(int*a,int len){int min;for(int i =0;i < len -1;i++){
        min = i;for(int j = i +1;j < len;j++){if(a[min]> a[j]){
                min = j;}}if(min != i){Swap(a,min,i);}}}

算法分析：

-平均时间复杂度：o(N^2),嵌套双循环
-时间复杂度：o(N^2)
-空间复杂度：o(1)
-稳定性：稳定的

4. 堆排序

基本思想：

将待排序序列构成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其于末尾元素进行交换，此时末尾就为最大值，然后将剩余n-1个元素重新构成一个堆，这样就会得到n个元素的次小值，如此反复执行就能得到一个有序序列。

步骤：
步骤一，构造初始堆。将给定的无序序列构造成一个大顶堆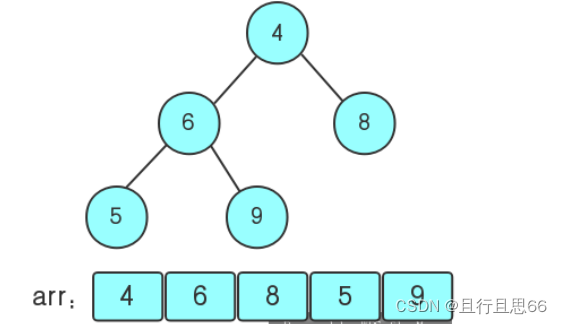

1.从最后一个非叶子节点开始，从左到右，从下到上进行调整。

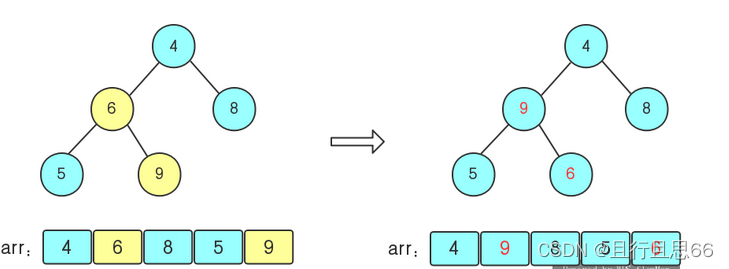
找到第二个非叶子节点4，因为{4,9,8}中9最大，则4和9交换

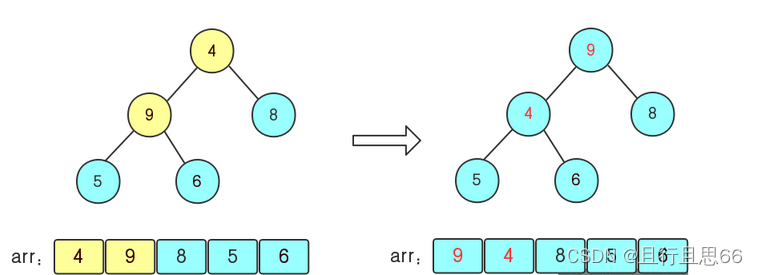
这时的交换使得{4，5，6}的结构发生变化，继续调整，{4，5，6}中6最大，交换4和6

步骤二：将堆顶元素与数组的末尾元素交换，使得末尾元素最大，然后继续调整堆结构，再将堆顶元素与末尾元素交换，得到第二大元素，如此反复交换、调整就可以得到一个有序序列。

1.将堆顶元素9与末尾元素4交换

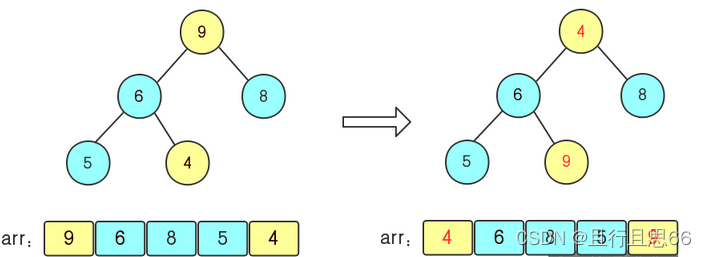
2.调整堆结构，让它继续满足堆定义

3.将堆顶元素8与末尾元素5交换，得到第二大元素8

4.将堆顶元素5与末尾元素4交换

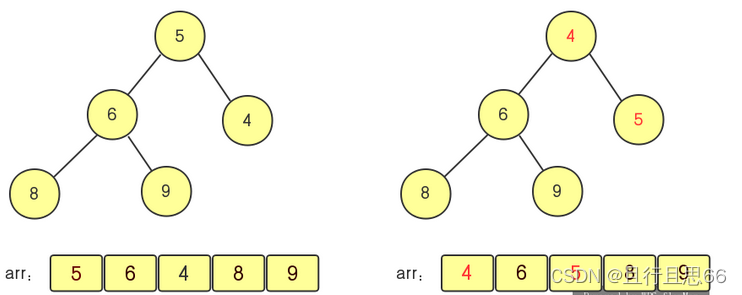
5.最后调整堆结构将5和6交换则得到了有序序列

代码：

voidAdjustdown(int*a,int root,int len){int parent = root;int child = parent *2+1;while(child<len){if(child < len -1&& a[child]<a[child+1]){
            child++;}if(a[parent]< a[child]){swap(*a,a[parent],a[child]);}
        parent = child;
        child =2* parent +1;}}voidCreateHeap(int*a,int len){for(int i = len /2-1; i >=0;i--){Adjustdown(a,i,len);}}voidHeapSort(int*a,int len){CreateHeap(a, len);int end = len;while(end >0){swap(*a,a[0],a[end-1]);
        end--;Adjustdown(a,0,end);}}

算法分析：

时间复杂度：o(N*logN)
稳定性：不稳定

5. 冒泡排序

原理：

从当前待排序列第一个开始遍历，指针从第一个开始，如果当前元素大于下一个，那么二者交换，指针往后走，当走到待排序列末尾时，最大的一定被放到了最后（像冒泡泡一样上去了），然后缩小待排子序列（把最后一个从当前待排序序列删去），如此循环直到当前待排子序列只有一个元素。

代码：

voidBubbleSort(int*a,int len){int i, j, temp;int flags =0;for(j =0; j < len -1; j++){for(i =0; i < len -1- j; i++){if(a[i]> a[i +1]){
                temp = a[i];
                a[i]= a[i +1];
                a[i +1]= temp;
                flags =1;//若不是有序的，flags设置为1；}}if(flags ==0)return;}}

算法分析：

• 平均时间复杂度：o(N^2),嵌套双循环
• 最好时间复杂度：o(N^2),每次要找最大最小肯定是要遍历一遍的
• 最坏时间复杂度：o(N^2)
• 空间复杂度：o(1)
• 稳定性：稳定的

6. 快速排序

原理：

1.从要排序的数据中取一个数为“基准数”。
2. 通过一趟排序将要排序的数据分割成独立的两部分，其中左边的数据都比“基准数”小，右边的数据都比“基准数”大。
3.然再按步骤2这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
4.挖坑填数 + 分治法
代码：

voidQuickSort(int*a,int low,int high){if(low>=high){return;}int i = low, j = high, index = a[i];//去最左边的数作为基准数indexwhile(i<j){while(i<j && a[j]>=index){//向左寻找第一个小于index的数
            j--;}if(i < j){
            a[i++]= a[j];// 将array[j]填入array[i]，并将i向右移动}while(i<j && a[i]<index){// 向右寻找第一个大于index的数
            i++;}if(i < j){
            a[j--]= a[i];// 将array[i]填入array[j]，并将j向左移动}}
    a[i]= index;//将基数填入最后的坑QuickSort(a, low, i -1);//递归调用，分治QuickSort(a, i +1, high);//递归调用，分治}

算法分析：

时间复杂度：O(n^2)
稳定性：稳定

7. 归并排序

原理：排序的思想就是将元素无限拆分，直到无可拆分为止，再将拆分的元素两两按序合并

voidprintList(int arr[],int len){int i;for(i =0; i < len; i++){printf("%d\t", arr[i]);}}voidmerge(int arr[],int start,int mid,int end){int result[ArrLen];int k =0;int i = start;int j = mid +1;while(i <= mid && j <= end){if(arr[i]< arr[j]){
            result[k++]= arr[i++];}else{
            result[k++]= arr[j++];}}if(i == mid +1){while(j <= end)
            result[k++]= arr[j++];}if(j == end +1){while(i <= mid)
            result[k++]= arr[i++];}for(j =0, i = start; j < k; i++, j++){
        arr[i]= result[j];}}voidmergeSort(int arr[],int start,int end){if(start >= end)return;int mid =(start + end)/2;mergeSort(arr, start, mid);mergeSort(arr, mid +1, end);merge(arr, start, mid, end);}

算法分析：

时间复杂度：O(nlog（n）)
稳定性：在合并的时候，如果两个数相等，可以将前面的数先放到辅助数组中，所以归并排序是稳定的

8.基数排序

思想：对数字的每一位进行排序，先对个位排序，然后十位，百位……，对每一位进行排序时，要求采用稳定排序算法，比如前面讨论过的计数排序。

voidradix(int*a,int length){int max=a[0];for(int i=1;i<length;i++)//找出最大值{if(a[i]>max){
               max=a[i];}}int base=1;int*b=(int*)malloc(sizeof(int)*length);//每次操作后元素的排序状态都会保存在这个中间过度数组中while(max/base>0)//循环的次数为最大值的位数，比如520是三位数，则循环三次{int t[10]={0};//声明并定义一个“桶数组”for(int i=0;i<length;i++)//实现上面第一个小图的功能{
           t[a[i]/base%10]++;}for(i=1;i<10;i++)//实现上面第二个小图的功能{
           t[i]+=t[i-1];}for(i=length-1;i>=0;i--){
           b[t[a[i]/base%10]-1]=a[i];
           t[a[i]/base%10]--;}for(i=0;i<length;i++)//赋值{
           a[i]=b[i];}
      base=base*10;}}

算法分析：

平均时间复杂度：O( n*k）k：为最大的位数
空间复杂度：O(m+n)空间复杂度我们也可以看出来,主要就是取决于链表的数量以及序列元素的数量,所以空间复杂度为O(n+k)

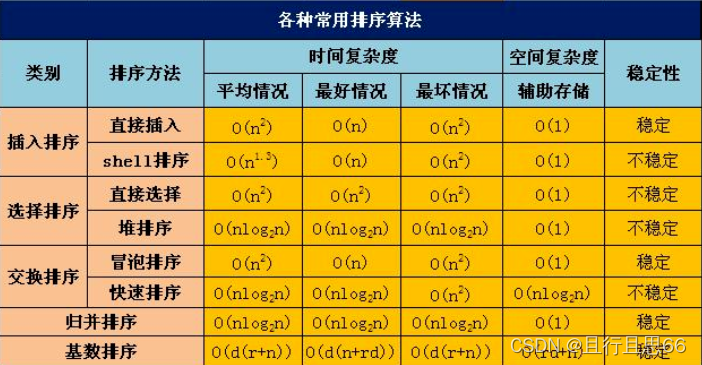
9.总结