1.请写出图像数字化的两个主要步骤,并简述其目的。
图像数字化:数字化坐标值称为取样,数字化幅度值称为量化。
- 取样:数字传感器只能在一组离散的级别上测量有限数量的样本。取样的目的在于将空间坐标离散化。
- 量化:取样值在灰度级值上还是连续分布的,为了形成数字函数,灰度值也必须转变为离散值。量化就是将连续的模拟信号转换为该信号的数字表示的过程。
2.请列举三种常见的图像灰度增强的算法。
- 线性变换(正比、反比/图像反转 s=L-1-r)
- 对数变换(s = c log(1+r) )
- 幂次变换(s = c r^y)
3.直方图均衡化的意义是什么?简述其处理步骤。
意义:若一幅图像的像素占有全部可能的灰度级并且分布均匀,则这样的图像有高对比度和多变的灰度色调。直方图均衡化仅仅依靠输入图像直方图中的信息即可自动地达到这一效果,生成一幅灰度级丰富且动态范围大的图像。

4.请画出拉普拉斯算子和Sobel算子分别对应的3×3模版。
基于二阶微分的拉普拉斯算子:
0 1 0
1 -4 1
0 1 0
基于一阶微分的Sobel算子:
-1 -2 -1 -1 0 1
0 0 0 -2 0 2
1 2 1 -1 0 1
5.请列举三种常见的色度空间模型,简述各个分量的意义 。
RGB:红、绿、蓝
HSI:色调、饱和度、亮度
CMYK:青、品红、黄、黑
YUV:亮度、色度
YCbCr:亮度、对蓝色和红色的偏移程度
6.请列举3种常见的YUV采样格式。
YCbCr
4:4:4
4:2:2
4:2:0
4:1:1
7.请列举原时域信号与傅立叶变换后频域信号在“ 连续性 / 离散性 ”与“ 周期性 / 非周期性”间的对应关系 。
- 傅里叶变换:
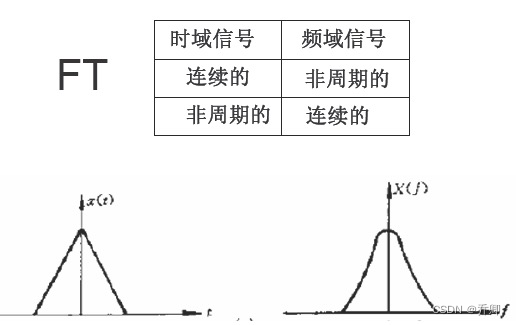
- 傅里叶级数:

- 离散序列傅里叶变换:

- 离散傅里叶变换:
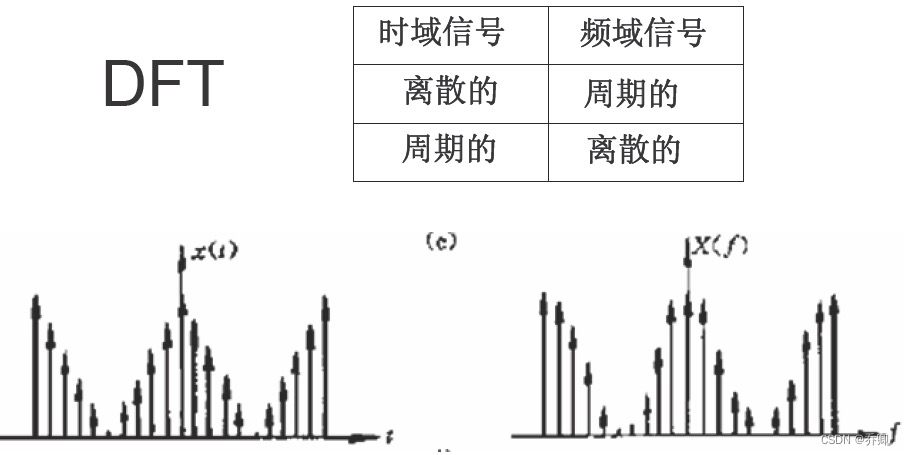
记忆:
傅里叶变换、离散傅里叶变换 不改变 性质
剩下两个 完全改变 性质
8.列举DFT变换的几种常见性质,如何利用其性质进行IDFT快速计算。

9.简述FFT算法两大特点。
- 变址:输出按照顺序,输入则是“码位倒置”的顺序,这种顺序称为倒位序,即二进制数倒位。 在实际运算中,直接将输入数据x(n)按码位倒置的顺序排列很不方便,一般总是先按自然顺序输入存储单元 ,然后通过变址运算将自然顺序的存储换成码位倒置顺序的存储,这样就可以进行FFT的原位运算。
- 原位运算:也称为同址运算,流程图中各蝶形对的输入量或输出量是互不相重的,任何一对蝶形的二个输入量经蝶形运算后 ,便失去了利用价值,不再需要保存。因此,当数据输入到存储器中以后,每一级运算的结果仍然存储在原来的存储器中,直到最后输出,中间无需其它的存储器。原位运算的结构可以节省存储单元,降低设备成本。
10.简述KL变换核的构造步骤 。 KL变换后的系数具有的特殊性质( 均值,协方差矩阵)?
KL变换是一种可以去掉随机向量中各元素间相关性的线性变换,可以将原始数据集合变换到主分量空间,使单一数据样本的互相关性降低到最低点。KL变换核的构造步骤为:

11.分别列举三种常见的频域低通/高通滤波器。其中,理想低通滤波器有什么缺点?
低通:理想低通、巴特沃斯低通滤波器、高斯低通滤波器
高通:理想高通、巴特沃斯高通滤波器、高斯高通滤波器
简单地截断傅里叶变换中的所有高频成分,这种陡峭的截止频率非物理可实现。由于理想低通滤波器的过度特性过于急峻,所以会产生比较严重的模糊和振铃现象,半径越小,模糊和振铃越明显。
12.同样是去噪,图像复原任务与图像增强任务有什么不同要求 ?
图像增强主要是一个主观的过程,而图像复原的大部分过程是一个客观的过程。
图像增强是一个探索性过程,为人类视觉系统的生理接受特点而设计一种改善图像的方法,增强图像的视觉效果。
图像复原试图利用退化现象的某种先验知识来重建或复原被退化的图像。
13.请列举三种常见的噪声模型。
高斯噪声、瑞利噪声、伽马噪声、指数分布噪声、均匀分布噪声、脉冲噪声(椒盐噪声)
14.请列举三种常见的图像去噪算法 。其中,哪种更适于去除椒盐噪声?哪种更适于去除高斯白噪声?
均值滤波器、中值滤波器、最大值和最小值滤波器、中点滤波器、修正后的阿尔法均值滤波器
- 最小值滤波器去除盐
- 最大值滤波器去除椒
- 中值滤波器去除椒盐
- 谐波均值滤波器去除高斯噪声
- 中点滤波器也可以去除高斯噪声
15.请设计一套改善以下图像质量的方法,简述处理流程。

该图像主要存在两个问题:(1)存在椒噪声、(2)整体灰度值偏低,图像过暗,对比度过低。
处理流程:首先用最大值滤波器对该图像进行滤波,之后进行直方图均衡化或对数变换以增强其对比度。
版权归原作者 乔卿 所有, 如有侵权,请联系我们删除。