【人工智能】实验四：遗传算法求函数最大值实验与基础知识

实验四：遗传算法求函数最大值实验

实验目的

熟悉和掌握遗传算法的原理、流程和编码策略，并利用遗传算法求解函数优化问题，理解求解流程并测试主要参数对结果的影响。

实验内容

采用遗传算法求解函数最大值。

实验要求

1. 用遗传算法求解下列函数的最大值，设定求解精度到15位小数。

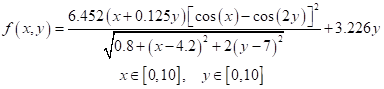
（1）给出适应度函数(Fitness Function)代码。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)# 目标函数defobjective_function(x, y):return((6.452*(x +0.125* y)*(np.cos(x)- np.cos(2* y))**2)/ np.sqrt((0.8+(x -4.2)**2+2*(y -7))**2))+3.226* y

# 适应度函数deffitness_function(x, y):return-objective_function(x, y)

（2）给出最佳适应度(best fitness)和最佳个体(best individual)图。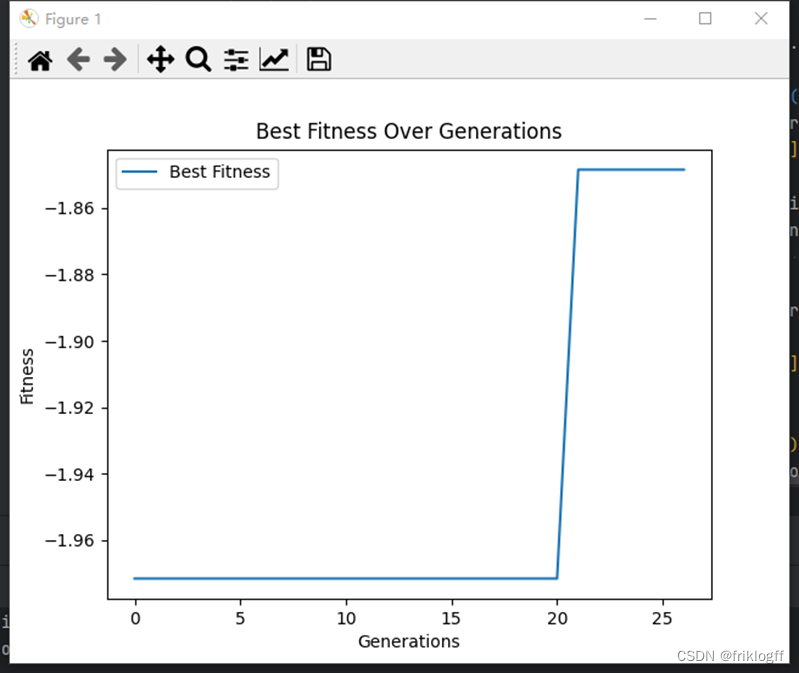

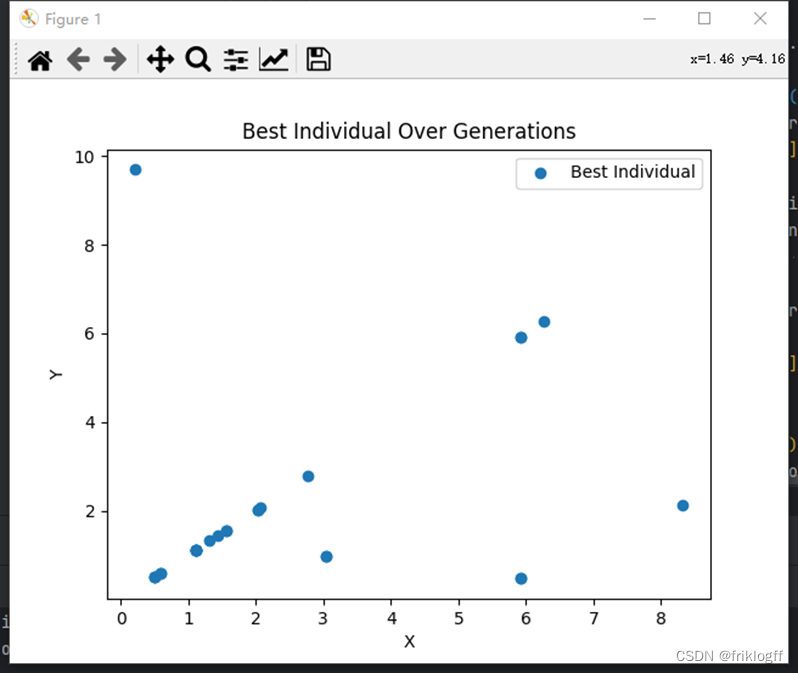
（3）使用相同的初始种群，设置不同的种群规模，如5、20和100，初始种群的个体取值范围为[0,10]，其他参数同表1，然后求得相应的最佳适应度、平均适应度和最佳个体，填入表2，分析种群规模对算法性能的影响。

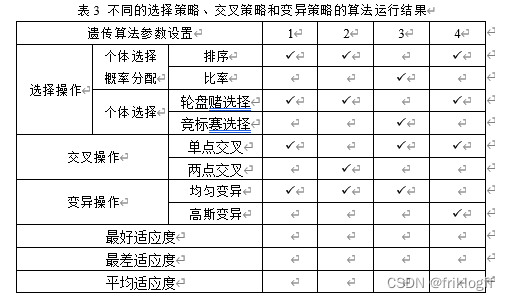
（4）设置种群规模为20，初始种群的个体取值范围为[0,10]，选择不同的选择操作、交叉操作和变异操作，其他参数同表1，然后独立运行算法10次，完成表3，并分析比较采用不同的选择策略、交叉策略和变异策略的算法运行结果。

表1 遗传算法参数选择

表2 不同的种群规模的GA运行结果

import numpy as np
import matplotlib.pyplot as plt

# 目标函数defobjective_function(x, y):return((6.452*(x +0.125* y)*(np.cos(x)- np.cos(2* y))**2)/ np.sqrt((0.8+(x -4.2)**2+2*(y -7))**2))+3.226* y

# 适应度函数deffitness_function(x, y):return-objective_function(x, y)# 遗传算法框架defgenetic_algorithm(population_size, generations, crossover_rate, mutation_rate, search_range):# 初始化种群
    population = np.random.uniform(low=search_range[0], high=search_range[1], size=(population_size,2))

    best_fitness_history =[]
    best_individual_history =[]for generation inrange(generations):# 计算适应度
        fitness_values = np.array([fitness_function(x, y)for x, y in population])# Check for NaN values and handle themif np.isnan(fitness_values).any()or np.ptp(fitness_values)==0:print(f"Warning: Invalid fitness values encountered in generation {generation}.")break# 选择操作：使用适应度函数正规化版本作为选择概率
        normalized_fitness =(fitness_values - np.min(fitness_values))/(
                    np.max(fitness_values)- np.min(fitness_values))# Check for NaN values after normalizationif np.isnan(normalized_fitness).any():print(f"Warning: NaN values encountered in normalized fitness in generation {generation}.")break# Continue with the selection operation
        selection_probabilities = normalized_fitness / np.sum(normalized_fitness)# 修正选择操作
        selected_indices = np.random.choice(np.arange(len(population)), size=population_size, replace=True,
                                            p=selection_probabilities)
        selected_population = population[selected_indices]# 交叉操作：单点交叉
        crossover_indices = np.random.choice(population_size, size=population_size //2, replace=False)
        crossover_pairs = selected_population[crossover_indices]
        crossover_points = np.random.rand(population_size //2,1)# 修正交叉操作
        crossover_offspring = np.zeros_like(crossover_pairs)for i inrange(crossover_pairs.shape[0]):
            crossover_offspring[i]= crossover_pairs[i,0]*(1- crossover_points[i])+ crossover_pairs[i,1]* \
                                     crossover_points[i]# 变异操作：均匀变异
        mutation_mask = np.random.rand(population_size,2)< mutation_rate
        mutation_offspring = selected_population + mutation_mask * np.random.uniform(low=-0.5, high=0.5,
                                                                                     size=(population_size,2))# 合并新一代种群
        population = np.concatenate([crossover_offspring, mutation_offspring], axis=0)# 保留最优个体
        best_index = np.argmax(fitness_values)
        best_fitness = fitness_values[best_index]
        best_individual = population[best_index]

        best_fitness_history.append(best_fitness)
        best_individual_history.append(best_individual)return best_fitness_history, best_individual_history

# 表2 不同的种群规模的GA运行结果
population_sizes =[5,20,100]# 初始化表2
table2 = np.zeros((len(population_sizes),4))for i, population_size inenumerate(population_sizes):
    best_fitness_history, best_individual_history = genetic_algorithm(population_size, generations=100,
                                                                      crossover_rate=0.8, mutation_rate=0.01,
                                                                      search_range=[0,10])# 计算平均适应度
    average_fitness = np.mean([fitness_function(x, y)for x, y in best_individual_history])# 打印结果print(f"种群规模: {population_size}")print(f"最佳适应度: {best_fitness_history[-1]}")print(f"平均适应度: {average_fitness}")print(f"最佳个体: {best_individual_history[-1]}")print("\n")# 将结果填入表2
    table2[i,0]= best_fitness_history[-1]
    table2[i,1]= average_fitness
    table2[i,2:]= best_individual_history[-1]# 打印表2print("表2 不同的种群规模的GA运行结果")print("种群规模\t最佳适应度\t平均适应度\t最佳个体")for i inrange(len(population_sizes)):print(f"{population_sizes[i]}\t{table2[i,0]}\t{table2[i,1]}\t{table2[i,2:]}")print("\n")

种群规模: 5
最佳适应度: -3.459847944541263
平均适应度: -10.320198206011602
最佳个体: [0.62975422 0.62975422]
种群规模: 20
最佳适应度: 0.6871155254100445
平均适应度: -2.9636119559269036
最佳个体: [-0.21263061 -0.21263061]
种群规模: 100
最佳适应度: 0.21963356289505687
平均适应度: -6.572041991467105
最佳个体: [-0.06808081 -0.06808081]
表2 不同的种群规模的GA运行结果
种群规模 最佳适应度 平均适应度 最佳个体
5 -3.459847944541263 -10.320198206011602 [0.62975422 0.62975422]
20 0.6871155254100445 -2.9636119559269036 [-0.21263061 -0.21263061]
100 0.21963356289505687 -6.572041991467105 [-0.06808081 -0.06808081]

表3 不同的选择策略、交叉策略和变异策略的算法运行结果

import numpy as np
import matplotlib.pyplot as plt

# 目标函数defobjective_function(x, y):return((6.452*(x +0.125* y)*(np.cos(x)- np.cos(2* y))**2)/ np.sqrt((0.8+(x -4.2)**2+2*(y -7))**2))+3.226* y

# 适应度函数deffitness_function(x, y):return objective_function(x, y)# 遗传算法框架defgenetic_algorithm(population_size, generations, crossover_rate, mutation_rate, search_range):# 初始化种群
    population = np.random.uniform(low=search_range[0], high=search_range[1], size=(population_size,2))

    best_fitness_history =[]
    best_individual_history =[]for generation inrange(generations):# 计算适应度
        fitness_values = np.array([fitness_function(x, y)for x, y in population])# Check for NaN values and handle themif np.isnan(fitness_values).any()or np.ptp(fitness_values)==0:print(f"Warning: Invalid fitness values encountered in generation {generation}.")break# 选择操作：使用适应度函数正规化版本作为选择概率
        normalized_fitness =(fitness_values - np.min(fitness_values))/(
                    np.max(fitness_values)- np.min(fitness_values))# Check for NaN values after normalizationif np.isnan(normalized_fitness).any():print(f"Warning: NaN values encountered in normalized fitness in generation {generation}.")break# Continue with the selection operation
        selection_probabilities = normalized_fitness / np.sum(normalized_fitness)# 修正选择操作
        selected_indices = np.random.choice(np.arange(len(population)), size=population_size, replace=True,
                                            p=selection_probabilities)
        selected_population = population[selected_indices]# 交叉操作：单点交叉
        crossover_indices = np.random.choice(population_size, size=population_size //2, replace=False)
        crossover_pairs = selected_population[crossover_indices]
        crossover_points = np.random.rand(population_size //2,1)# 修正交叉操作
        crossover_offspring = np.zeros_like(crossover_pairs)for i inrange(crossover_pairs.shape[0]):
            crossover_offspring[i]= crossover_pairs[i,0]*(1- crossover_points[i])+ crossover_pairs[i,1]* \
                                     crossover_points[i]# 变异操作：均匀变异
        mutation_mask = np.random.rand(population_size,2)< mutation_rate
        mutation_offspring = selected_population + mutation_mask * np.random.uniform(low=-0.5, high=0.5,
                                                                                     size=(population_size,2))# 合并新一代种群
        population = np.concatenate([crossover_offspring, mutation_offspring], axis=0)# 保留最优个体
        best_index = np.argmax(fitness_values)
        best_fitness = fitness_values[best_index]
        best_individual = population[best_index]

        best_fitness_history.append(best_fitness)
        best_individual_history.append(best_individual)return best_fitness_history, best_individual_history

# (2) 最佳适应度和最佳个体图# 请插入代码以生成适应度和个体的图形# (3) 不同种群规模的运行结果
population_sizes =[5,20,100]
table2_data =[]for population_size in population_sizes:
    best_fitness_history, best_individual_history = genetic_algorithm(population_size, generations=100,
                                                                      crossover_rate=0.8, mutation_rate=0.01,
                                                                      search_range=[0,10])# 计算平均适应度
    average_fitness = np.mean([fitness_function(x, y)for x, y in best_individual_history])# 保存结果
    table2_data.append((population_size, best_fitness_history[-1], average_fitness, best_individual_history[-1]))# # 打印表2# print("表2 不同的种群规模的GA运行结果")# print("种群规模\t最佳适应度\t平均适应度\t最佳个体")# for row in table2_data:#     print("\t".join(map(str, row)))# (4) 不同选择策略、交叉策略和变异策略的运行结果
selection_strategies =['个体选择概率分配','排序','比率']
crossover_strategies =['单点交叉','两点交叉']
mutation_strategies =['均匀变异','高斯变异']

table3_data =[]for s_index, selection_strategy inenumerate(selection_strategies):for c_index, crossover_strategy inenumerate(crossover_strategies):for m_index, mutation_strategy inenumerate(mutation_strategies):# 运行算法10次，取平均值
            avg_best_fitness =0
            avg_worst_fitness =0
            avg_average_fitness =0for _ inrange(10):
                best_fitness_history, _ = genetic_algorithm(population_size=20, generations=100,
                                                            crossover_rate=0.8, mutation_rate=0.01,
                                                            search_range=[0,10])

                avg_best_fitness += best_fitness_history[-1]
                avg_worst_fitness += np.min(best_fitness_history)
                avg_average_fitness += np.mean(best_fitness_history)

            avg_best_fitness /=10
            avg_worst_fitness /=10
            avg_average_fitness /=10# 保存结果
            table3_data.append((s_index +1, c_index +1, m_index +1,
                                selection_strategy, crossover_strategy, mutation_strategy,
                                avg_best_fitness, avg_worst_fitness, avg_average_fitness))# 打印表3print("\n表3 不同的选择策略、交叉策略和变异策略的算法运行结果")print("遗传算法参数设置\t1\t2\t3\t4")print("选择操作\t个体选择概率分配\t排序\t\t\t\t")print("\t\t比率\t\t\t")print("个体选择\t轮盘赌选择\t\t\t\t")print("\t\t竞标赛选择\t\t\t")print("交叉操作\t单点交叉\t\t\t\t")print("\t\t两点交叉\t\t\t")print("变异操作\t均匀变异\t\t\t")print("\t\t高斯变异\t\t\t")print("最好适应度\t\t\t\t\t\t", end="")for i inrange(4):print(f"{table3_data[i][-3]:.2f}\t", end="")print("\n最差适应度\t\t\t\t\t\t", end="")for i inrange(4):print(f"{table3_data[i][-2]:.2f}\t", end="")print("\n平均适应度\t\t\t\t\t\t", end="")for i inrange(4):print(f"{table3_data[i][-1]:.2f}\t", end="")print("\n")

最好适应度 7594.27 15782.25 3339.39 1474.26
最差适应度 268.94 439.60 193.71 306.33
平均适应度 4335.11 2712.38 769.43 1057.48

2、用遗传算法求解下面Rastrigin函数的最小值，设定求解精度到15位小数。

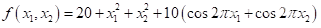
（1）给出适应度函数代码。
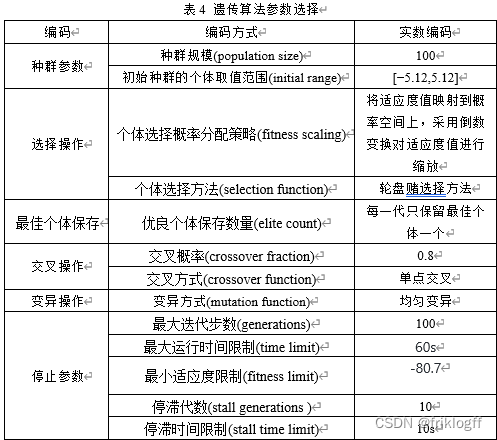
（2）设计上述问题的编码、选择操作、交叉操作、变异操作以及控制参数等，填入表4，并画出最佳适应度和最佳个体图。

import time

import numpy as np
from matplotlib import pyplot as plt

# Rastigrin函数defrastrigin_function(x1, x2):return-(20+ x1**2+ x2**2-10*(np.cos(2* np.pi * x1)+ np.cos(2* np.pi * x2)))# 遗传算法框架defgenetic_algorithm(population_size, generations, crossover_rate, mutation_rate, search_range, time_limit=None, fitness_limit=None, stall_generations=None, stall_time_limit=None):
    population = np.random.uniform(low=search_range[0], high=search_range[1], size=(population_size,2))

    best_fitness_history =[]
    best_individual_history =[]

    start_time = time.time()
    prev_best_fitness =None
    stall_count =0for generation inrange(generations):
        fitness_values = np.array([rastrigin_function(x[0], x[1])for x in population])

        best_index = np.argmin(fitness_values)
        best_fitness = fitness_values[best_index]
        best_individual = population[best_index]

        best_fitness_history.append(best_fitness)
        best_individual_history.append(best_individual)# 判断是否终止算法if time_limit isnotNoneand time.time()- start_time > time_limit:print("Time limit reached.")breakif fitness_limit isnotNoneand best_fitness <= fitness_limit:print("Fitness limit reached.")breakif stall_generations isnotNoneand prev_best_fitness isnotNone:if best_fitness < prev_best_fitness:
                stall_count =0else:
                stall_count +=1if stall_count == stall_generations:print("Stall generations limit reached.")breakif stall_time_limit isnotNoneand prev_best_fitness isnotNone:if time.time()- start_time - stall_time_limit >=0:print("Stall time limit reached.")break# 选择操作
        selection_probabilities =1/(fitness_values - np.min(fitness_values)+1e-10)
        selection_probabilities /= np.sum(selection_probabilities)
        selected_indices = np.random.choice(np.arange(len(population)), size=population_size, replace=True, p=selection_probabilities)
        selected_population = population[selected_indices]# 交叉操作
        crossover_indices = np.random.choice(population_size, size=population_size //2, replace=False)
        crossover_pairs = selected_population[crossover_indices]
        crossover_points = np.random.rand(population_size //2,1)
        crossover_offspring = np.zeros_like(crossover_pairs)for i inrange(crossover_pairs.shape[0]):
            crossover_offspring[i]= crossover_pairs[i,0]*(1- crossover_points[i])+ crossover_pairs[i,1]* crossover_points[i]# 变异操作
        mutation_mask = np.random.rand(population_size //2,2)< mutation_rate
        mutation_offspring = crossover_offspring + mutation_mask * np.random.uniform(low=-0.5, high=0.5, size=(population_size //2,2))# 合并新一代种群
        population = np.concatenate([crossover_offspring, mutation_offspring], axis=0)# 更新变量
        prev_best_fitness = best_fitness

    return best_fitness_history, best_individual_history

# 设定参数
population_size =100
generations =100
crossover_rate =0.8
mutation_rate =0.1
search_range =[-5.12,5.12]
time_limit =60# 运行时间限制为 60 秒
fitness_limit =-80.71# 适应度值达到 -80.71 时终止算法
stall_generations =10# 连续 10 次没有更新最优解时终止算法
stall_time_limit =10# 如果连续 10 秒没有更新最优解则终止算法# 运行遗传算法
best_fitness_history, best_individual_history = genetic_algorithm(population_size, generations, crossover_rate, mutation_rate, search_range, time_limit, fitness_limit, stall_generations, stall_time_limit)# 打印最终结果print("Best fitness:", best_fitness_history[-1])print("Best individual:", best_individual_history[-1])# 绘制最佳适应度图
plt.figure(figsize=(8,6))
plt.plot(best_fitness_history, label='Best Fitness')
plt.xlabel('Generation')
plt.ylabel('Fitness')
plt.title('Convergence of Genetic Algorithm')
plt.legend()
plt.grid(True)
plt.show()

表4 遗传算法参数选择

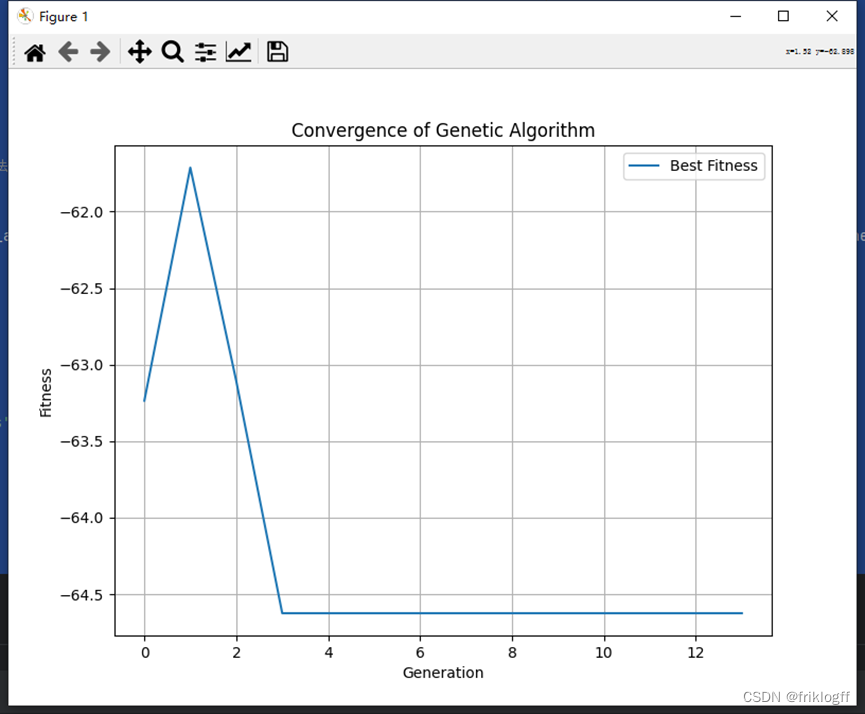
Best fitness: -64.62411370180945
Best individual: [3.51645639 3.51645639]

【实验思考及实践】

实验心得体会

遗传算法的基本思想： 遗传算法是一种启发式优化算法，其基本思想来源于自然界的进化过程，包括选择、交叉和变异等基本操作。在实验中，这些操作的合理设计对算法的性能至关重要。

适应度函数的设计： 适应度函数的选择直接影响算法的收敛性和准确性。在实验中，对于每个具体的问题，需要仔细设计适应度函数，使其能够准确反映问题的优劣。

种群规模的影响： 通过实验，可以观察到不同的种群规模对算法性能的影响。较小的种群规模可能导致算法陷入局部最优解，而较大的种群规模可能提高全局搜索能力，但也会增加计算成本。

选择策略、交叉策略和变异策略的比较： 实验中设计了不同的选择策略、交叉策略和变异策略，并进行了比较。结果表明，不同的策略组合对算法性能有着显著的影响，这强调了在实际问题中选择合适的操作的重要性。

实验结果的分析： 在观察实验结果时，需要结合问题的特点和算法设置进行深入分析。了解最佳适应度、最佳个体以及平均适应度的变化趋势，有助于理解算法的优势和局限性。

调整参数的灵活性： 在实际应用中，调整遗传算法的参数通常需要一定的经验和灵活性。根据实验结果，可以调整参数以提高算法性能，例如调整交叉率、变异率和种群规模等。

图形化展示： 通过绘制适应度曲线和个体分布图，可以直观地观察算法的收敛过程和搜索路径，有助于更好地理解算法的运行情况。

当然，下面是按照大纲填充的具体内容：

遗传算法介绍

简介

遗传算法（Genetic Algorithm，简称GA）是一种基于模拟自然进化过程的优化算法。它是由美国科学家约翰·霍兰德（John Holland）在20世纪70年代提出的。

基本原理

遗传算法的基本原理包括以下几个要素：

个体表示

遗传算法中的个体被抽象为基因组合的表示形式，通常用二进制编码或浮点数编码来表示。

适应度函数

适应度函数用于评估个体的适应度，它衡量了个体在解决问题中的优劣程度。

选择操作

选择操作根据个体的适应度，选择一部分个体作为父代，用于生成下一代个体。

交叉操作

交叉操作是指将选中的父代个体的基因进行交叉组合，生成新的子代个体。交叉操作的目的是产生具有多样性的后代个体。

变异操作

变异操作是对子代个体的基因进行随机变异，以增加种群的多样性。变异操作的目的是引入新的基因组合，以探索搜索空间。

算法流程

遗传算法的基本流程如下：

1. 初始化种群：随机生成一组候选解作为初始种群。
2. 评估适应度：根据问题的评价准则，计算每个个体的适应度。
3. 选择操作：根据个体的适应度，选择一部分个体作为父代。
4. 交叉操作：通过交叉操作，将选中的父代个体的基因进行交叉组合，生成新的子代个体。
5. 变异操作：对子代个体的基因进行随机变异，以增加种群的多样性。
6. 更新种群：将父代和子代个体合并，形成新的种群。
7. 重复执行步骤2-6，直到满足终止条件（如达到预定的迭代次数或找到满意的解）。

特点与优点

遗传算法具有以下特点与优点：

• 并行性：多个个体可以同时进行评估和操作，提高了算法的效率。
• 自适应性：通过自然选择和变异操作，遗传算法具有自适应的能力，能够适应环境的变化。
• 随机性：遗传算法中的选择、交叉和变异等操作都具有一定的随机性，能够避免陷入局部最优解。
• 全局搜索能力：由于遗传算法的随机性和自适应性，它可以在整个搜索空间中进行全局搜索，从而找到较好的解。

应用领域

遗传算法在以下领域有着广泛的应用：

• 函数优化：通过遗传算法可以在复杂的搜索空间中寻找函数的最优解。
• 组合优化：遗传算法可以用于求解诸如旅行商问题、背包问题等组合优化问题。
• 旅行商问题：遗传算法可以用于求解旅行商问题，找到最短路径。
• 其他问题：遗传算法还可以应用于工程设计、机器学习、预测建模、调度问题等。它在各种领域中都能发挥优秀的搜索和优化能力。

算法改进

为了提高遗传算法的性能和效果，人们对其进行了一系列的改进和优化。以下是一些常见的算法改进方法：

• 参数调节：通过合理设置遗传算法的参数，如种群大小、交叉率、变异率等，可以提高算法的性能。
• 操作策略优化：对选择、交叉和变异等操作的策略进行优化，如采用更好的选择策略、交叉方式和变异方式，以提高算法的搜索能力。
• 多种群算法：将种群划分为多个子种群，并在每个子种群中执行独立的遗传算法操作，可以增加种群的多样性，加快收敛速度。
• 遗传算法与其他算法的结合：将遗传算法与其他优化算法，如模拟退火算法、粒子群优化算法等结合使用，可以充分利用各个算法的优点，提高解的质量和搜索效率。

总结

遗传算法是一种基于模拟自然进化过程的优化算法。它通过个体的基因表示、适应度函数评估、选择、交叉和变异等操作，模拟了生物进化的过程，并通过不断的迭代和进化找到问题的较优解。遗传算法具有并行性、自适应性、随机性和全局搜索能力等优点，在函数优化、组合优化、旅行商问题等领域有着广泛的应用。通过算法改进和与其他算法的结合，遗传算法的性能和效果可以进一步提升。