一、冒泡排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动
1.1 动态图
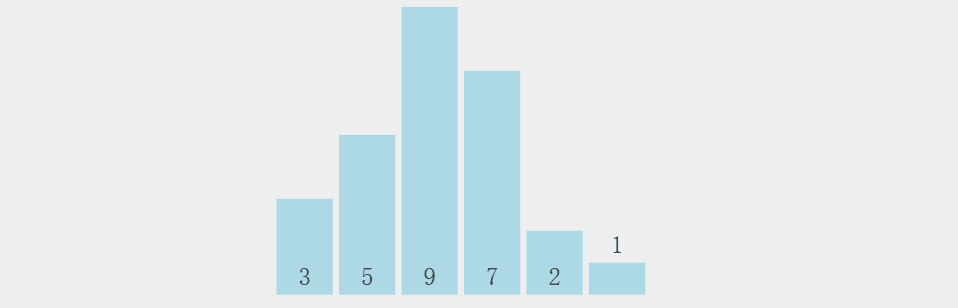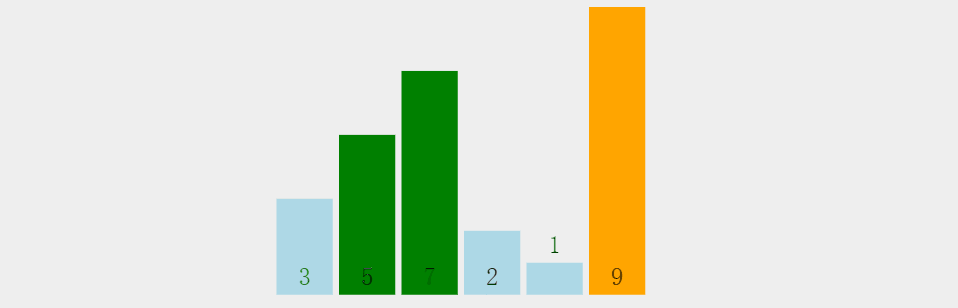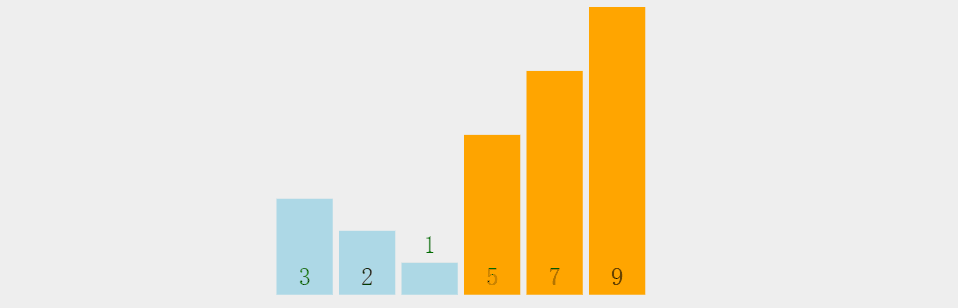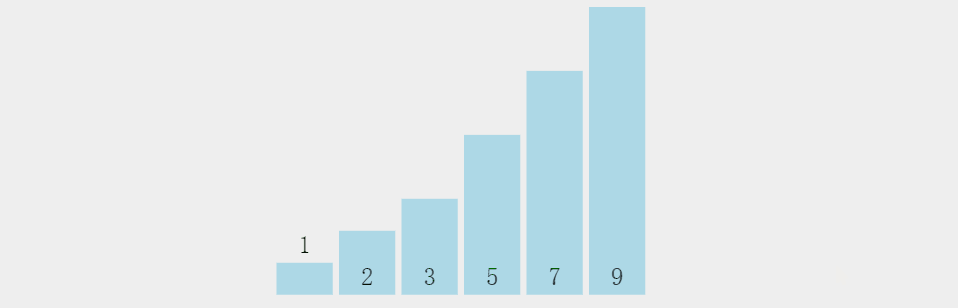
1.2 代码
//冒泡排序
void BubbleSort(int* a,int n)
{
//第一次排的是[0,n-1],第二次[0,n-2]...所以外循环不如控制后面的数(n-1 ,n-2 ....)
for (int j = n-1;j > 0;j--)//n个数要进行n-1趟
{
for (int i = 0; i < j; i++)//一趟,即把最大数放在最后面
{
if (a[i] > a[i + 1])
{
Swap(&a[i], &a[i + 1]);
}
}
}
}
运行结果:
1.3 优化
思想:一趟交换之后,一个都没有进行交换,那么说明就是有序的,则可以用一个flag进行标记
//冒泡排序优化
void BubbleSort(int* a, int n)
{
for (int j = n - 1; j > 0; j--)
{
int flag = 1;//写在这里如果第一次完成了有序,则第二次之后就可以不进行冒泡了
for (int i = 0; i < j; i++)
{
if (a[i] > a[i + 1])
{
Swap(&a[i], &a[i + 1]);
flag = 0;
}
}
if (flag == 1)
{
break;
}
}
}
运行结果:
1.4 特性
冒泡排序是一种非常容易理解的排序
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
1.5 三种排序的比较
直接插入排序、直接选择排序、冒泡排序,这三种排序在最坏的情况下都是o(n^2)
其中三者之间效率最差的是直接选择排序,其无论在什么场景下都是o(n^2)
其次是冒泡排序的效率更差一些,因为直接插入排序和冒泡排序最坏情况下是一样的,所以可以比较最好的情况,而优化冒泡和直接插入排序最好的情况下也都是o(n)。
对于已经有序的数组排序,他们一样好,但是对于接近有序的数组,直接插入排序更好,比如 1 2 3 4 6 5 ,优化冒泡的比较次数为 n-1 + n - 2 ,直接插入比较次数为 n,所以综合而言,直接插入更好一些。
所以从差到优的顺序为: 直接选择排序 < 冒泡排序 < 直接插入排序
二、快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右 子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
2.1 hoare版本静态图
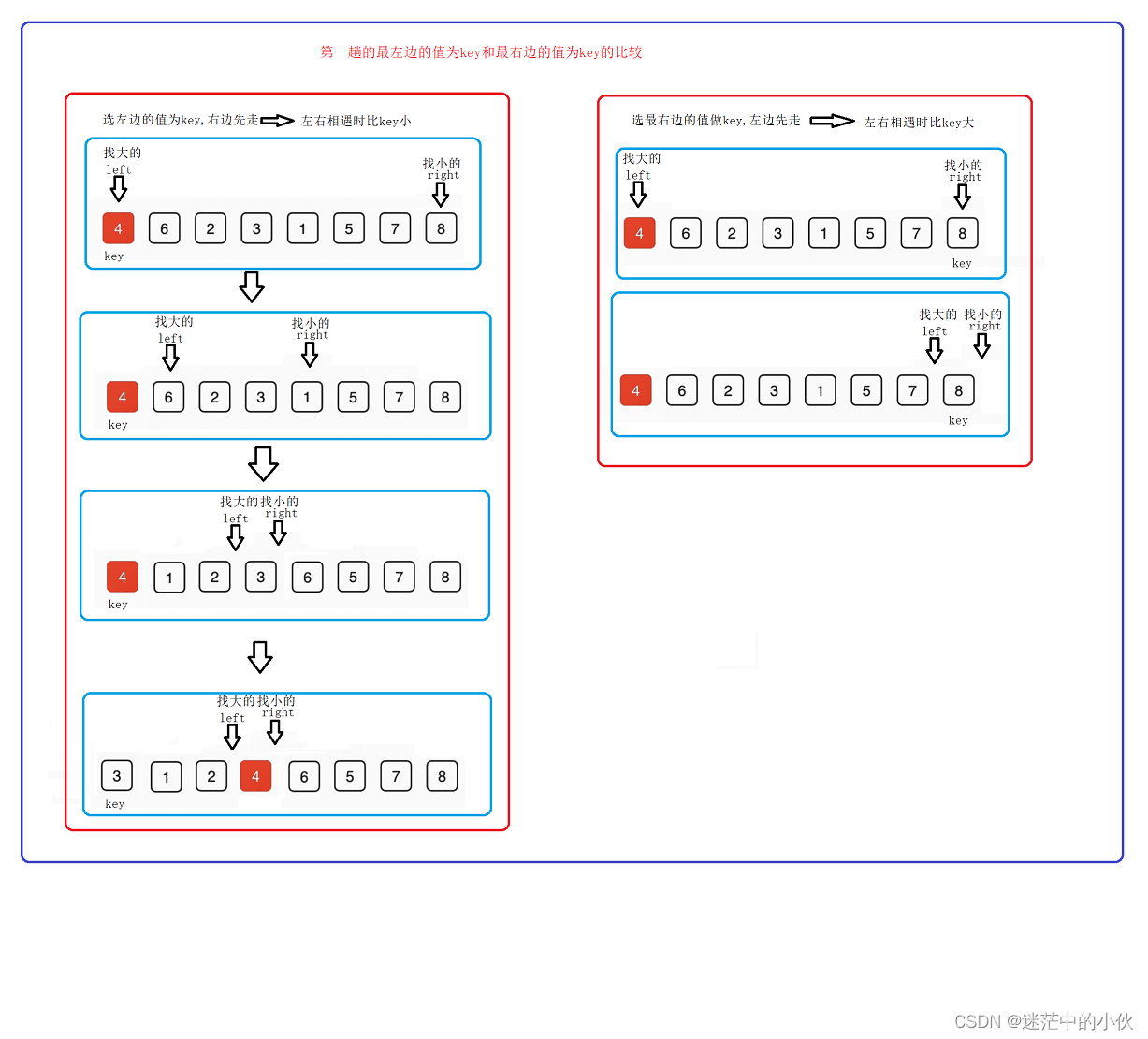
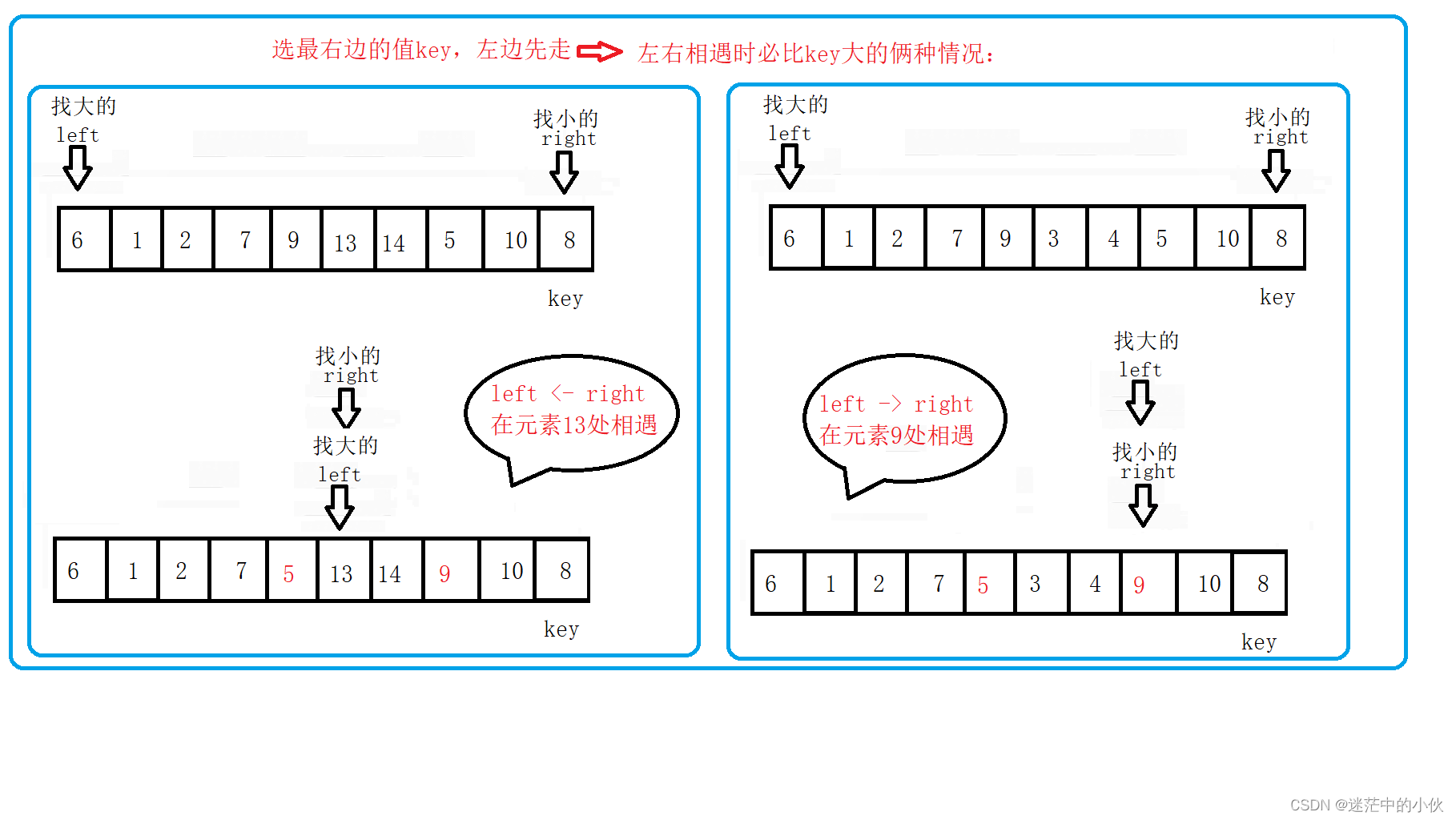
2.2 单趟 容易出现的问题
//单趟
void Partion(int* a,int left,int right)
{
//设置最左边为key
int keyi = left;
while (left < right)
{
//右边先走,找小值
while (a[right] > a[keyi])
{
right--;
}
//左边再走,找大值
while (a[left] < a[keyi])
{
left++;
}
//进行交换
Swap(&a[left],&a[right]);
}
//最后左右相遇点的值再与key交换
Swap(&a[left],a[keyi]);
}
上述的快速排序单趟为错误的版本,有俩个特殊场景可能会导致代码错误:
2.2.1 特殊场景一
如果 数组中的数为 5 5 5 5 5,那么a[right] > a[keyi] 和a[left] < a[keyi],根本不会进入条件语句内,但是每次都会进行Swap,一直进行while循环,造成死循环。
解决办法:
改成a[right] >= a[keyi] 和 a[left] <= a[keyi] ,也就是当值与key的值相等时,就把相等的那个值放在key的右边或放在其左边,最后left和right会在第一个5处相遇,但是a[right] == key ,right--,会导致越界。
2.2.2特殊场景二:
如果数组中的数为 5 6 7 8 9 , 9 >= 5,8 >=5 , 7 >= 5,6 >= 5, 5 >= 5 ,right--,然后right 就越界了
解决办法:
将while (a[right] > a[keyi]) 中再进行一次判断,如果left < right ,那么right就不会越界了,while (a[left] < a[keyi])也如此
2.3 单趟 正确的代码为(hoare版本)
//单趟 [left,right] hoare版本
int Partion(int* a,int left,int right)
{
//设置最左边为key
int keyi = left;
while (left < right)
{
//右边先走,找小值
while(left < right && a[right] >= a[keyi])//right == left 表明没有比key小的数了
{
right--;
}
//左边再走,找大值
while(left < right && a[left] <= a[keyi])//left == right 表明没有比key大的数了
{
left++;
}
//进行交换
Swap(&a[left],&a[right]);
}
//最后左右相遇点的值再与key交换
Swap(&a[left],&a[keyi]);
return left;
}
2.4 整体代码(递归)
//单趟 [left,right] hoare版本
int Partion(int* a,int left,int right)
{
//设置最左边为key
int keyi = left;
while (left < right)
{
//右边先走,找小值
while(left < right && a[right] >= a[keyi])//right == left 表明没有比key小的数了
{
right--;
}
//左边再走,找大值
while(left < right && a[left] <= a[keyi])//left == right 表明没有比key大的数了
{
left++;
}
//进行交换
Swap(&a[left],&a[right]);
}
//最后左右相遇点的值再与key交换
Swap(&a[left],&a[keyi]);
return left;
}
void QuickSort(int* a,int left,int right)
{
//出口,没有区间时
if (left >= right)
{
return;
}
//对key左右区间再进行排序
int keyi = Partion(a,left,right);
//[0,keyi-1] keyi [keyi+1 , right]
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);
}
运行结果:
2.5 递归分析
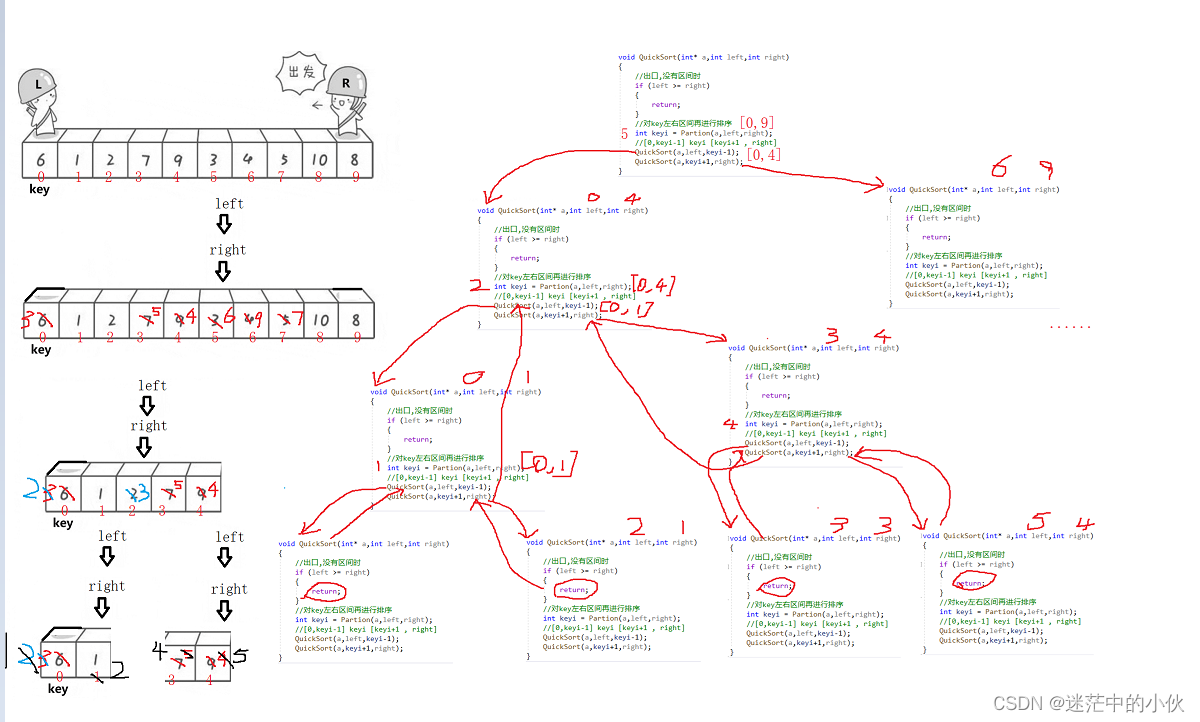
2.6 特性
快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
时间复杂度:O(N*logN) (假设每次选的key是中位数)
空间复杂度:O(logN)
稳定性:不稳定
2.7 快速排序有序数组优化:三数取中法
如果数列是无序的,杂乱无章的,那么快速排序效率是非常快的,然而快速排序也存在着缺陷,当数组为有序数组时,如下图: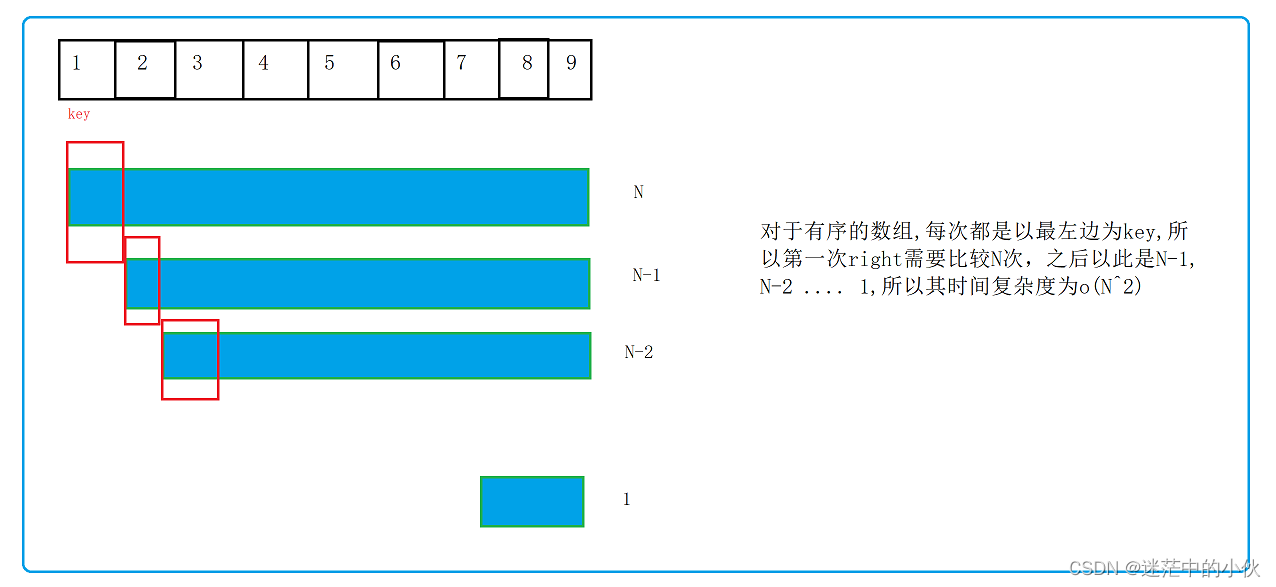
2.7.1 问题1:那么有什么方法可以解决快速排序有序数组的问题呢?
这里我们运用的是三数取中法。
三数取中法:在快排的过程中,每一次我们要取一个元素作为枢纽值,以这个数字来将序列划分为两部分。在此我们采用三数取中法,也就是取左 端、中间、右端三个数,然后进行排序,将中间数作为枢纽值。就算不是有序的数组,有时没有问题的,他会保证不是最大的数或者最小的数作为key,然而此方法主要解决的还是快速排序有序数组的问题
2.7.2 问题2:为什么要解决快速排序优化有序数组的问题呢?
因为此次运用的是递归的方法,而递归的缺陷就在于一下俩点。
1.相比循环程序,性能差。(针对早起编译器,因为对于递归调用,建立栈帧优化不大.现在编译器优化都很好,递归相比循环相差不大)
2.递归太深,会导致栈溢出的现象。
2.7.3 问题3:那么为什么要取中间值呢?
假设待排序的数组是升序有序数组,那么left处应该是最小值,right处应该是最大值,此时如果我们选取一个排在中间的值,即使在最坏的情况下,left和right只需要走到中间位置,那么这个中间值的位置也就确定了下来,而不需要left和right把整个数组遍历一遍,大大提高了排序的效率.也就相当于下图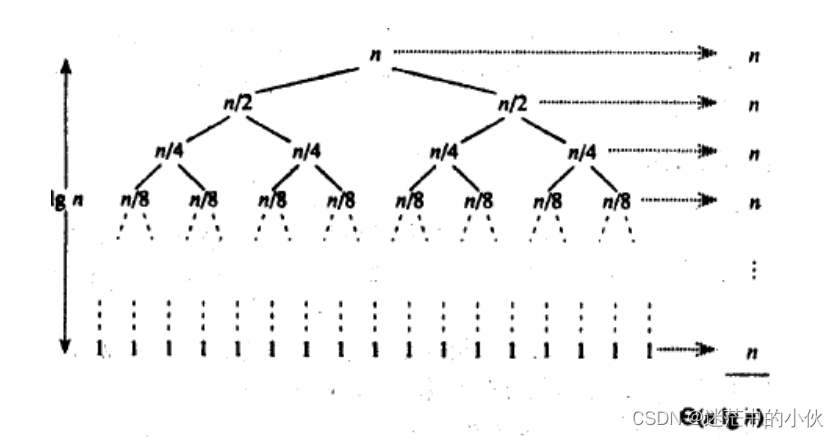
每次选取key是中位数,最后的时间复杂度为o(n * logn),此时就不会导致栈溢出,因为像二叉树一样,向外扩散,栈帧不会调用层次太高。
2.8 优化代码(三数取中法)
//三数取中法
int GetMiddleIndex(int* a, int left, int right)
{
int middle = left + ((right - left) >> 1);//为了防止left和right的值都超过int 的一半,相加会越界
if (a[left] < a[middle])//不一定是有序数组,所以考虑多种情况
{
if (a[middle] < a[right])
{
return middle;
}
else if (a[left] > a[right])
{
return left;
}
else //left < right<middle
{
return right;
}
}
else // a[left] > a[middle]
{
if (a[left] < a[right])
{
return left;
}
else if (a[middle] > a[right])
{
return middle;
}
else
{
return right;
}
}
}
//单趟 [left,right] hoare版本
int Partion(int* a,int left,int right)
{
//将中间值放到最左边
int mini = GetMiddleIndex(a,left,right);
Swap(&a[mini],&a[left]);
//设置最左边为key
int keyi = left;
while (left < right)
{
//右边先走,找小值
while(left < right && a[right] >= a[keyi])//right == left 表明没有比key小的数了
{
right--;
}
//左边再走,找大值
while(left < right && a[left] <= a[keyi])//left == right 表明没有比key大的数了
{
left++;
}
//进行交换
Swap(&a[left],&a[right]);
}
//最后左右相遇点的值再与key交换
Swap(&a[left],&a[keyi]);
return left;
}
void QuickSort(int* a,int left,int right)
{
//出口,没有区间时
if (left >= right)
{
return;
}
//对key左右区间再进行排序
int keyi = Partion(a,left,right);
//[0,keyi-1] keyi [keyi+1 , right]
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);
}
2.9 单趟 方法二:挖坑法
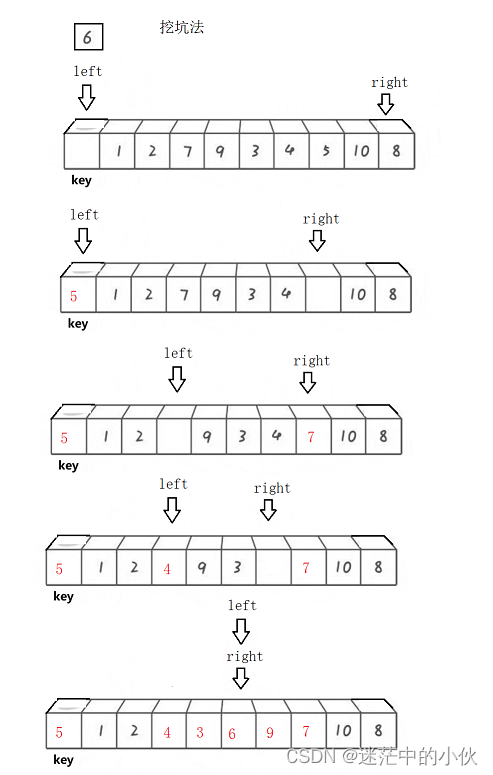
2. 10 挖坑法代码
//挖坑法(没有设置变量pivot版本)
int Partion2(int* a, int left, int right)
{
//将中间值放到最左边
int mini = GetMiddleIndex(a, left, right);
Swap(&a[mini], &a[left]);
int key = a[left];
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[left] = a[right];
if (right != left)
{
left++;
}
while (left < right && a[left] <= key)
{
left++;
}
a[right] = a[left];
if (right != left)
{
right--;
}
}
a[left] = key;
return left;
}
//挖坑法(设置变量pivot版本)
int Partion3(int* a, int left, int right)
{
//将中间值放到最左边
int mini = GetMiddleIndex(a, left, right);
Swap(&a[mini], &a[left]);
int key = a[left];
int pivot = left;//设置坑
while (left < right)
{
while (left < right && a[right] >= key)
{
right--;
}
a[pivot] = a[right];//右边的值放到坑里,然后自己编程坑
pivot = right;
while (left < right && a[left] <= key)
{
left++;
}
a[pivot] = a[left];
pivot = left;
}
a[pivot] = key;
return pivot;
}
void QuickSort(int* a,int left,int right)
{
//出口,没有区间时
if (left >= right)
{
return;
}
//对key左右区间再进行排序
int keyi = Partion3(a,left,right);
//[0,keyi-1] keyi [keyi+1 , right]
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);
}
运行结果:
2.11 单趟方法三 前后指针法

2.12 代码
//前后指针法1
int Partion4(int* a, int left, int right)
{
//将中间值放到最左边
int mini = GetMiddleIndex(a, left, right);
Swap(&a[mini], &a[left]);
int prev = left;
int cur = prev + 1;
int keyi = left;
while (cur <= right)
{
while (cur <= right && a[cur] >= a[keyi])
{
cur++;
}//容易出现的问题:找到了最小值,交换之后,cur就不会变动了,所以交换完之后cur++,要一直往后找
if (cur <= right)
{
++prev;
Swap(&a[cur], &a[prev]);
cur++;
}
}
//prev下标的值和keyi下标的值交换
Swap(&a[keyi],&a[prev]);
return prev;
}
//前后指针法2
int Partion5(int* a, int left, int right)
{
//将中间值放到最左边
int mini = GetMiddleIndex(a, left, right);
Swap(&a[mini], &a[left]);
int prev = left;
int cur = prev + 1;
int keyi = left;
while (cur <= right)
{
//Partion4 主要是俩个while循环,都检查cur < right,那么就会导致有些重复运行,一直需要判断
//而Partion5 更加简洁
//cur下标位置的值不管是比key大还是小都要往后走
//那可以有这个思路,cur一直往后走,但是当a[cur] < a[keyi]时,停下来交换一下
if (a[cur] < a[keyi] && ++prev != cur )//如果++prev之后和cur的位置一样,那么也就是自己和自己交换,那么没意思,不如直接不换
{
Swap(&a[cur],&a[prev]);
}
++cur;//cur是要一直向后走的
}
//prev下标的值和keyi下标的值交换
Swap(&a[keyi], &a[prev]);
return prev;
}
运行结果:
版权归原作者 迷茫中的小伙 所有, 如有侵权,请联系我们删除。