数据挖掘学习——SOM网络聚类算法+python代码实现

1.SOM简述

   SOM（Self Organizing Map）自组织映射网络，又称竞争型神经网络。可以通过将高维数据映射到结构和相互关系简单的低维空间中进行展示，从而实现数据可视化、聚类、分类等功能。
   SOM网络与其他的神经网络不同，比起其他的神经网络，他更接近于Kmeans聚类算法，即K-近邻聚类算法。
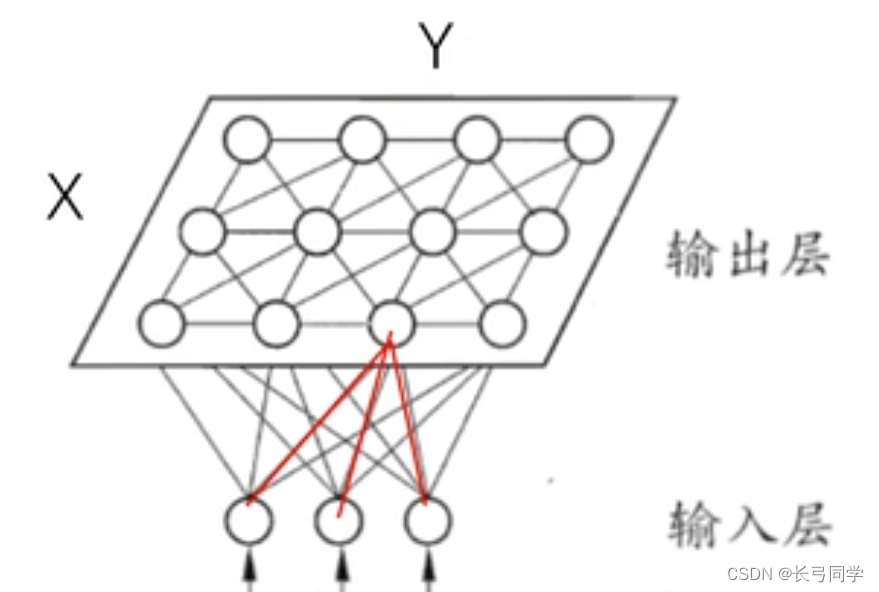
   其结构如下图所示。

从图中可以看到，输出层的每个节点，通过D条权边与输入节点相连（即输出层的每个节点用一个D维权重Wij来表征），其中输出层中每个节点之间按照距离远近存在一定联系。

2.SOM训练过程

（1）初始化

为初始权向量选择随机值

（2）采样（抽取样本点）

从输入数据中抽取一个样本点，作为输入训练向量样本

（3）竞争

对于权向量，神经元计算它们各自的判别函数值，为竞争提供基础。具有最小判别函数值的特定神经元被宣布为胜利者。（判别函数可定义为输入训练向量样本和权向量之间的平方欧几里德距离）

大白话：计算各个神经元和第二步选取的训练样本点之间的拓扑距离，距离最近的就是胜出的权向量点（winner）

（4）合作和适应（更新权重值）

在神经生物学研究中，我们发现在一组兴奋神经元内存在横向的相互作用。当一个神经元被激活时，最近的邻居节点往往比那些远离的邻居节点更兴奋。并且存在一个随距离衰减的拓扑邻域。

上一步胜出的神经元将获得权重值的决定权。不仅获胜的神经元能够得到权重更新，它的邻居也将更新它们的权重，尽管不如获胜神经元更新的幅度大。

可以理解为最近的权向量节点向样本点移动一定距离，同时邻近节点也移动一定的距离。

（5）重复

回到第二步重复，直到匹配完所有的输入数据点

3.python 代码实现

（1）初始化

    def __init__(self, X, output, iteration, batch_size):
        """
        :param X:  形状是N*D， 输入样本有N个,每个D维
        :param output: (n,m)一个元组，为输出层的形状是一个n*m的二维矩阵
        :param iteration:迭代次数
        :param batch_size:每次迭代时的样本数量
        初始化一个权值矩阵，形状为D*(n*m)，即有n*m权值向量。权值由numpy随机函数生成。
        """
        self.X = X
        self.output = output
        self.iteration = iteration
        self.batch_size = batch_size
        self.W = np.random.rand(X.shape[1], output[0] * output[1])
        print(self.W.shape)

（2）计算样本点和权向量之间的拓扑距离

    def GetN(self, t):
        """
        :param t:时间t, 这里用迭代次数来表示时间
        :return: 返回一个整数，表示拓扑距离，时间越大，拓扑邻域越小
        """
        a = min(self.output)
        return int(a - float(a) * t / self.iteration)
    def Geteta(self, t, n):
        """
        :param t: 时间t, 这里用迭代次数来表示时间
        :param n: 拓扑距离
        :return: 返回学习率，
        """
        return np.power(np.e, -n) / (t + 2)

（3）竞争

 def train(self):
        """
        train_Y:训练样本与形状为batch_size*(n*m)
        winner:一个一维向量，batch_size个获胜神经元的下标
        :return:返回值是调整后的W
        """
        count = 0
        while self.iteration > count:
            train_X = self.X[np.random.choice(self.X.shape[0], self.batch_size)]
            normal_W(self.W)
            normal_X(train_X)
            train_Y = train_X.dot(self.W)
            winner = np.argmax(train_Y, axis=1).tolist()
            self.updata_W(train_X, count, winner)
            count += 1
        return self.W
    def train_result(self):
        normal_X(self.X)
        train_Y = self.X.dot(self.W)
        winner = np.argmax(train_Y, axis=1).tolist()
        print(winner)
        return winner

（4）更新权重

    def updata_W(self, X, t, winner):
        N = self.GetN(t)
        for x, i in enumerate(winner):
            to_update = self.getneighbor(i[0], N)
            for j in range(N + 1):
                e = self.Geteta(t, j)
                for w in to_update[j]:
                    self.W[:, w] = np.add(self.W[:, w], e * (X[x, :] - self.W[:, w]))
    def getneighbor(self, index, N):
        """
        :param index:获胜神经元的下标
        :param N: 邻域半径
        :return ans: 返回一个集合列表，分别是不同邻域半径内需要更新的神经元坐标
        """
        a, b = self.output
        length = a * b
        def distence(index1, index2):
            i1_a, i1_b = index1 // a, index1 % b
            i2_a, i2_b = index2 // a, index2 % b
            return np.abs(i1_a - i2_a), np.abs(i1_b - i2_b)
        ans = [set() for i in range(N + 1)]
        for i in range(length):
            dist_a, dist_b = distence(i, index)
            if dist_a <= N and dist_b <= N: ans[max(dist_a, dist_b)].add(i)
        return ans