数据结构之二叉树（简单使用及知识点）

1.1二叉树定义

二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

结点的层次是从根开始定义的，根为第一层，根的孩子为第二层。若结点在l层则其子树就在l+1层。其双亲在同一层的结点互为堂兄弟。下图中D,E,F为堂兄弟。树中结点的最大层次称为树的深度或高度，下图树的深度为5.

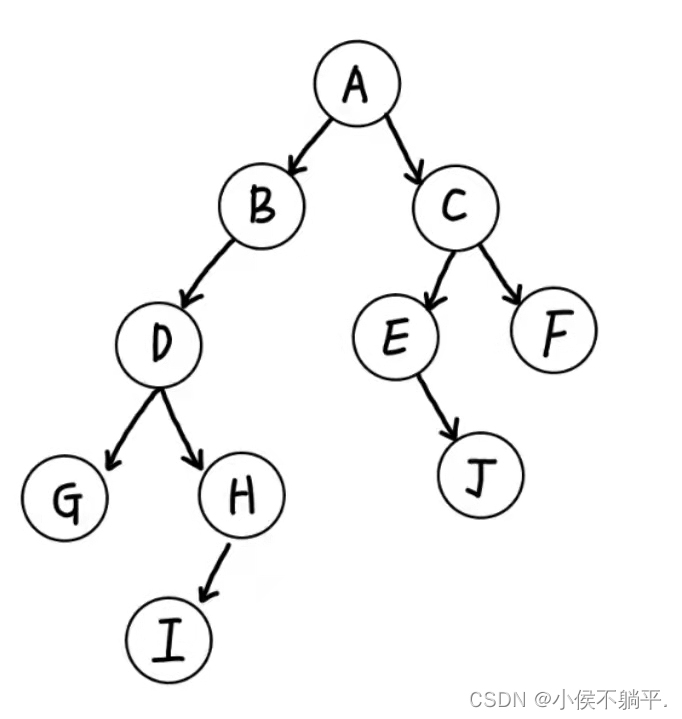上图为二叉树的表示

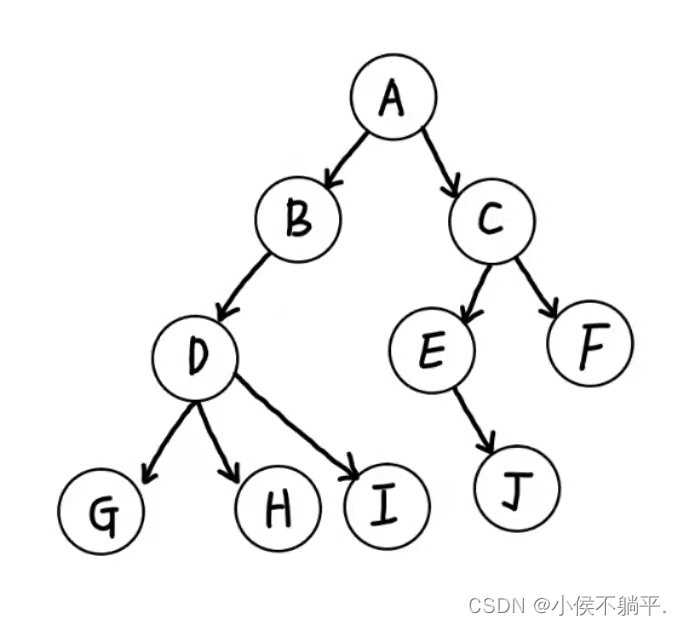**上图因为D结点有三个子树所以它不是二叉树 **

1.2 二叉树的特点

二叉树的特点有：

1）每个结点最多有两颗字数，所以二叉树不存在度大于2的结点，注意不是只有两棵子树，而是最多有两颗。没有子树或者有一颗子树都是可以的。

2）左子树和右子树是有顺序的，次序不能任意颠倒。就像人有双手、双脚。但显然左手、左脚和右手、右脚是不一样的，右手戴左手套、右脚穿左鞋都会极其的别扭和难受。

3）即使树中某结点只有一颗子树，也要区分它是左子树还是右子树，左子树和右子树都是一颗树，但它们确实不同的二叉树。就好像你一不小心，摔伤了手，伤到了右手还是左手，对你的生活影响程度是不同的。

二叉树具有一下五种基本形态：

（1）空二叉树

（2）只有一个根结点

（3）根结点只有左子树

（4）根结点只有右子树

（5）根结点既有左子树也有右子树

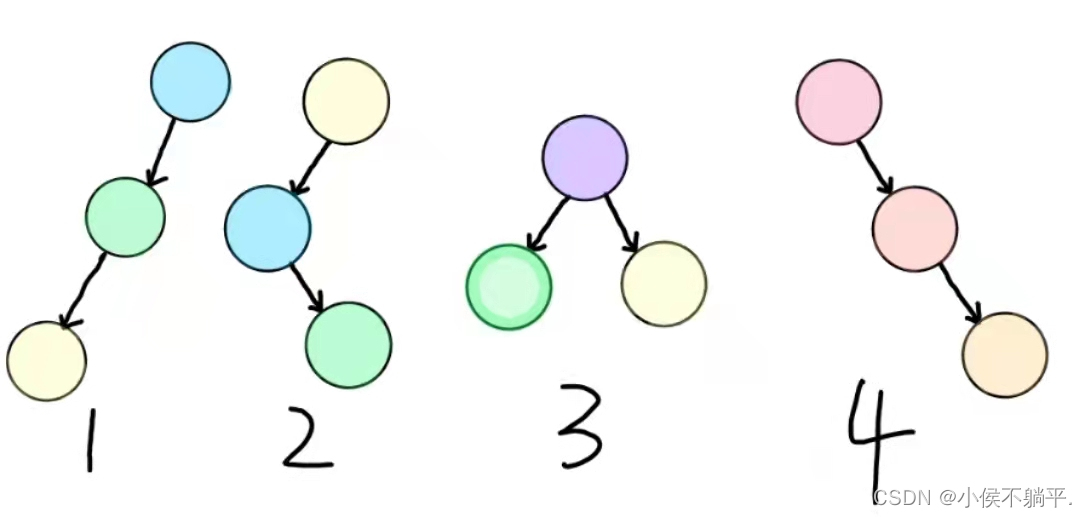
图1和图2都是根结点只有左子树，图3是根结点既有左子树也有右子树，图4是根结点只有右子树

1.3 特殊的二叉树

1.3.1 斜树

顾名思义，斜树一定要是斜的，但是往哪斜还是有讲究的。所有的结点都只是左子树的二叉树叫做左斜树。所有结点都只有右子树的二叉树叫做右斜树。这两者统称为斜树

如上面的图形，图1和图4分别是左斜树和右斜树。

1.3.2 满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

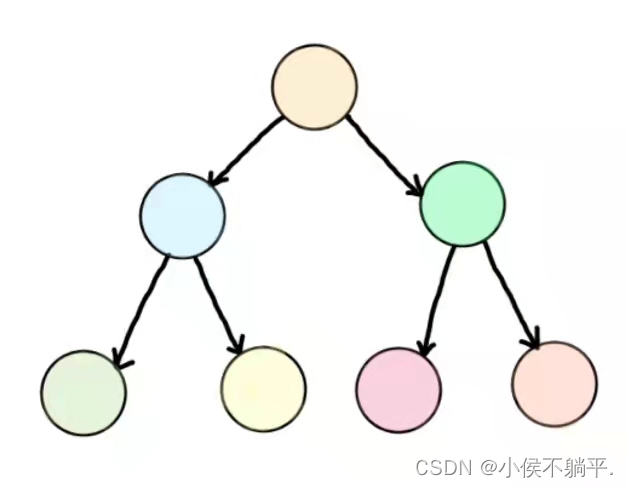
在同一深度下的二叉树中，满二叉树的结点和叶子的个数是最多的。

但是每个结点都存在左右子树，不能算是满二叉树，还必须要所有的叶子都在同一层上，这就做到了整棵树的平衡。因此，满二叉树的特点有：

1）叶子只能出现在最下一层。出现在其他层就不可能达到平衡

2）非叶子结点的度一定是2，否则就是“缺胳膊少腿了”

3）在同样深度二叉树中，满二叉树的结点个数最多，叶子数最多。

1.3.3 完全二叉树

对一颗具有n个结点的二叉树按层编号，如果编号为 i 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树，如下图所示：

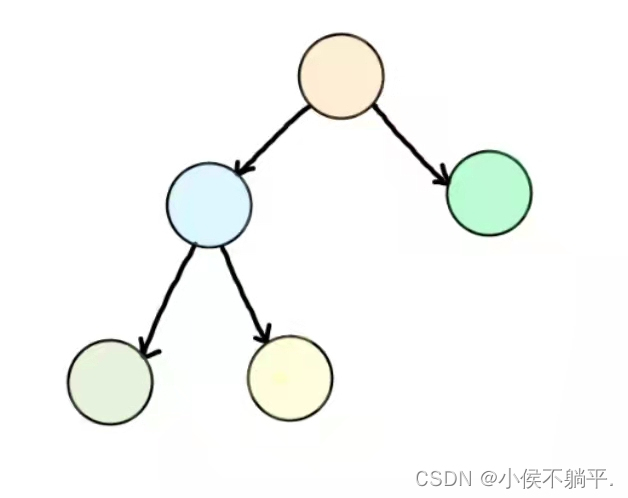
1.4 二叉树的性质

1.4.1 在二叉树的第 i 层至多有2^（i-1）个结点 （i>=1）

1.4.2 深度为k的二叉树至多有2^（k）-1个结点（k>=1）

1.4.3 对任何一颗二叉树T，如果其终端结点数为n，度为2的结点数为n2，则n=n2+1

1.4.4 具有n个结点的完全二叉树的深度为【log2(n)】+1

1.4.5 如果对一颗有n个结点的完全二叉树的结点按层序编号（从左至右）对于任一结点 i 有：

1）如果 i =1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是结点【i/2】

2）如果2i>n 则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i

3）如果2i+1>n,则结点i无右孩子；否则其右孩子是结点2i+1

1.5 二叉树结构体创建

struct student
{
    char name[25];
    int num;
    struct student *lchild,*rchild;
};

其中lchild和rchild分别指向该结点的左孩子和右孩子

1.6 二叉树的创建（利用递归算法）

struct student* create()
{
    struct student *p;
    p = (struct student*)malloc(sizeof(struct student));
    cin >> p->name >> p->num;
    if(p->num == 0)
        p = NULL;
    p->lchild = create();
    p->rchild = create();
    return 0;
}
        

建立二叉树时先从最左边开始建立直到左边全部建立完成之后再建立右边，不熟练的时候可以先自己画图进行思考自己把数据到底存到哪里了。

1.7 二叉树遍历

二叉树遍历是指从根结点出发，按照某种次序一次访问二叉树中的所有结点，使得每个结点被访问一次且仅仅被访问一次。

1.7.1 前序遍历

规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

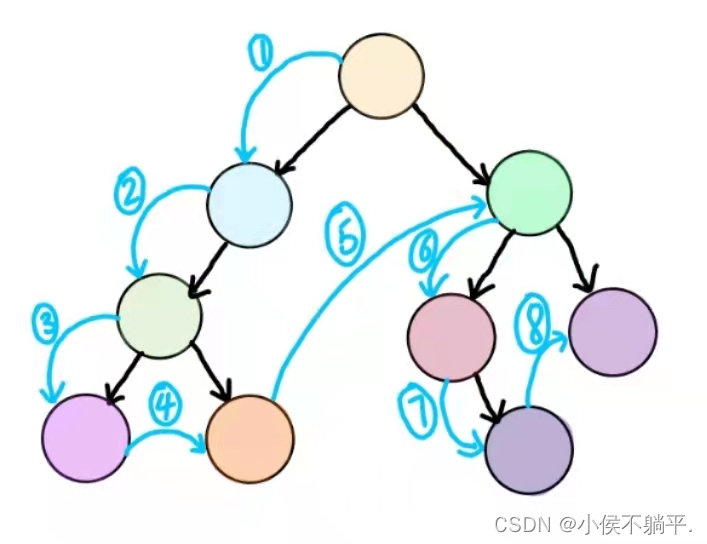
具体遍历的代码如下

void print(struct student *p)
{
    if(p == NULL)
        return ;
    cout << p->name <<" " << p->num;    //显示数据
    print(p->lchild);        //先遍历左子树
    print(p->rchild);        //先序遍历右子树
}

1.7.2 中序遍历

规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。

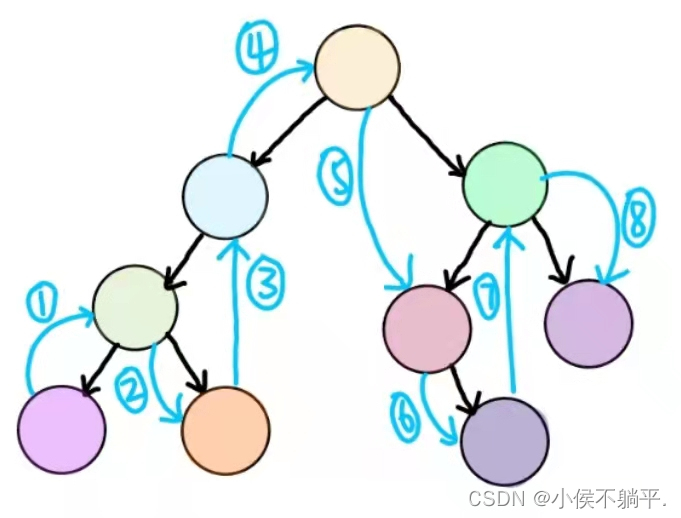
具体的实现代码如下：

void print(struct student *p)
{
    if(p == NULL)
        return ;
    print(p->lchild);        //先遍历左子树
    cout << p->name <<" " << p->num;    //显示数据
    print(p->rchild);        //先序遍历右子树
}

1.7.3 后序遍历

规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后访问根结点，如下图所示：

具体实现代码如下：

void print(struct student *p)
{
    if(p == NULL)
        return ;
    print(p->lchild);        //先遍历左子树
    print(p->rchild);        //先序遍历右子树
    cout << p->name <<" " << p->num;    //显示数据
}

1.8 整体实现创建并且遍历二叉树的代码如下：

#include<iostream>
#include<stdlib.h>
using namespace std;

struct student {
    char name[28];
    int num;
    struct student* lchild, * rchild;
};

struct student* create()        //创建一个二叉树利用递归算法
{
    struct student* p;
    p = (struct student*)malloc(sizeof(struct student));
    cin >> p->name >> p->num;
    if (p->num == 0)        //如果学号为0则不存在此人
        p = NULL;
    else
    {
        p->lchild = create();
        p->rchild = create();
    }
    return p;
}

void print1(struct student* p)        //前序遍历二叉树，利用递归算法
{
    if (p == NULL)
        return;
    cout << "\t" << p->name << "\t" << p->num << endl;
    print1(p->lchild);
    print1(p->rchild);
}

void print2(struct student* p)    //中序遍历二叉树，利用递归算法
{
    if (p == NULL)
        return;
    print2(p->lchild);
    cout << "\t" << p->name << "\t" << p->num << endl;
    print2(p->rchild);
}

void print3(struct student* p)    //后序遍历二叉树,利用递归算法
{
    if (p == NULL)
        return;
    print3(p->lchild);
    print3(p->rchild);
    cout << "\t" << p->name << "\t" << p->num << endl;
}

int main()
{
    struct student* phead;
    cout << "\t请输入学生的基本信息:" << endl;
    phead = create();
    cout << "前序遍历的结果:" << endl;
    cout << "\t姓名\t学号" << endl;
    print1(phead);
    cout << "中序遍历的结果:" << endl;
    cout << "\t姓名\t学号" << endl;
    print2(phead);
    cout << "后序遍历的结果:" << endl;
    cout << "\t姓名\t学号" << endl;
    print3(phead);
    return 0;
}

运行结果如图：

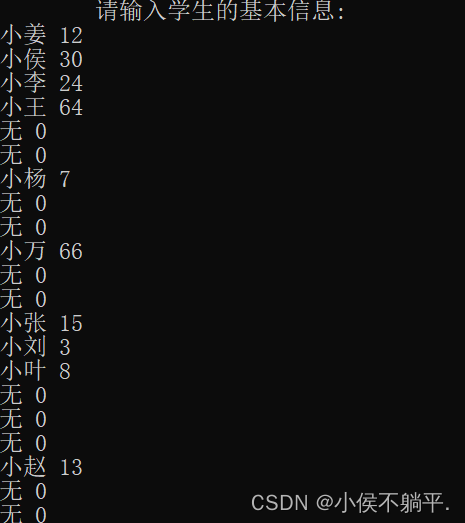
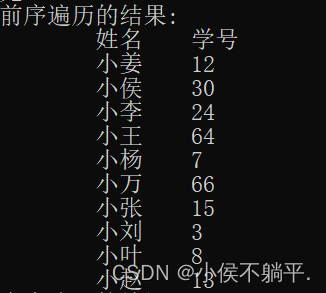
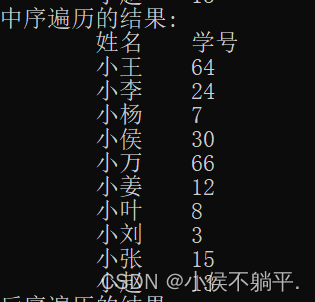
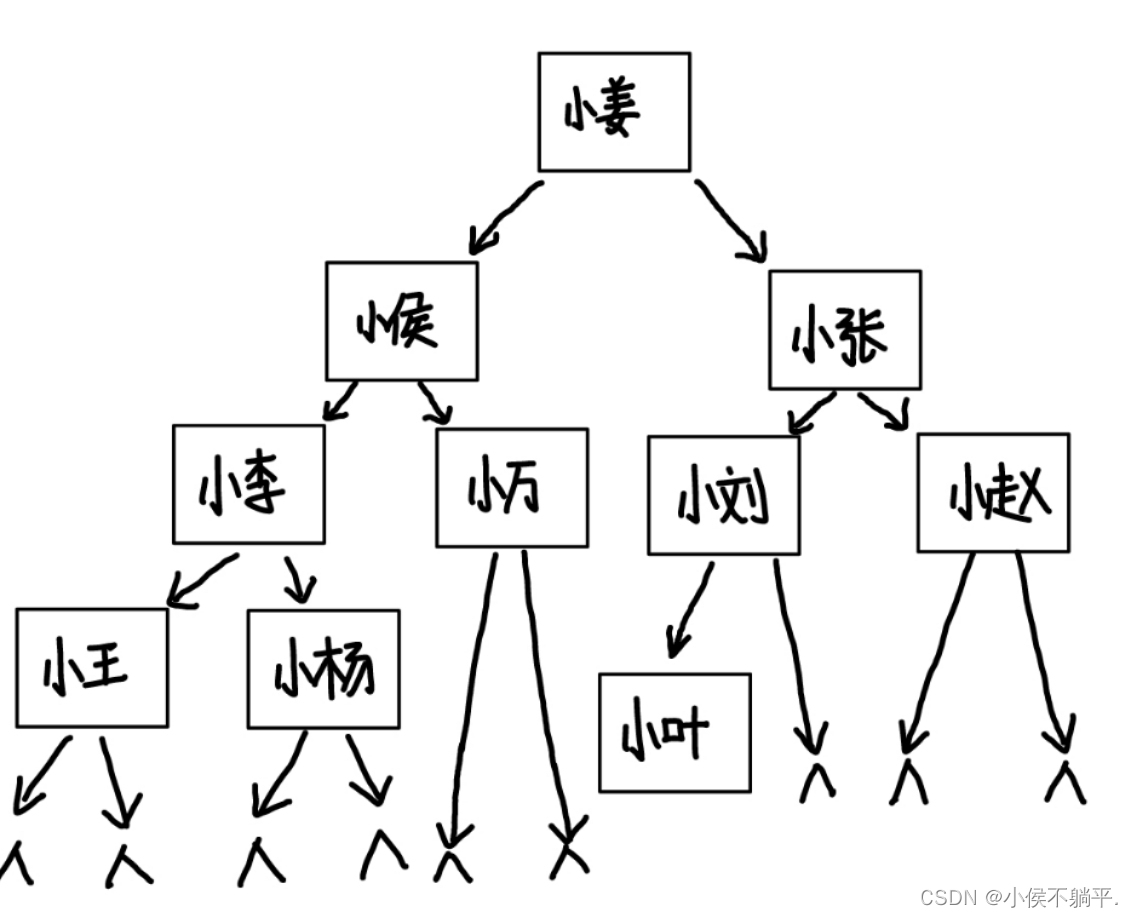
具体存储的形式我用一张图表示了一下，大家可以看一下

今天要讲述的就是这些内容，实现一个简单的二叉树就是你看完这篇文章应该要掌握的东西，希望大家可以通过观看往期的博客对c++有一个初步的认识以及自己的理解。