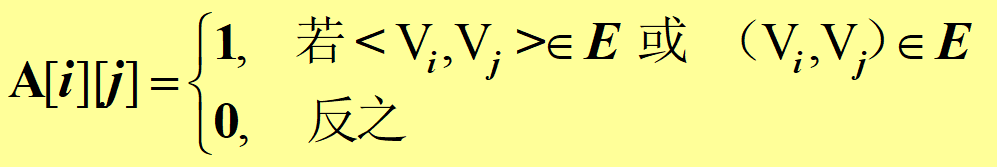🌺图的基本介绍
🍁图的基本概念
在图形结构中,结点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。因此,图的应用更为广泛。
🍁 图的定义
Q:什么是最大堆
A:图 G 由两个集合 V 和 E 组成,记作 G=(V,E) 。其中 V 是顶点的有穷非空集合,E 是 V 中顶点偶对的有穷集合,这些顶点偶对称为边。V(G) 和 E(G) 通常分别表示图 G 的顶点集合和边集合。 E(G) 可以为空集,若 E(G) 为空集,则图 G 只有顶点而没有边。

🌺图的基本术语
1)有向图
Q:什么是有向图
A:若E是有向边(也称弧)的有限集合时,则图 G 为有向图。弧是顶点的有序对,记为 <v, w> ,其中 v,w 是顶点,v 称为弧尾,w 称为弧头,<v,w> 称为从顶点 v 到顶点 w 的弧,也称 v 邻接到w,也称为 w 邻接自 v 。
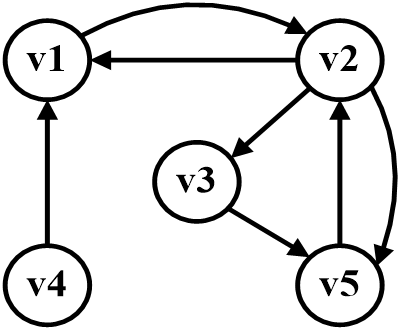
有向图 G:
G=(V,E)
V(G)={v1,v2,v3,v4,v5}
E(G)={<v1,v2>,<v2,v1>,<v2,v3>,<v2,v5>,<v3,v5>,<v4,v1>,<v5,v2>}
2)无向图
Q:什么是无向图
A:若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的无序对,记为 (v, w) 或 (w,v) ,因为 (v,w)=(w,v) , 其中 v,w 是顶点。可以说顶点 w 和顶点 v 互为邻接点。边 (v, w) 依附于顶点 w 和 v ,或者说边( v, w) 和顶点 v, w 相关联。
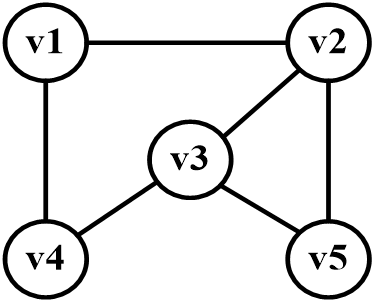
无向图 G:
G=(V,E)
V(G)={v1,v2,v3,v4,v5}
E(G)={(v1,v2),(v1,v4),(v2,v4),(v3,v4),(v3,v5)}
3)简单图
Q:什么是简单图
A:一个图 G 若满足:不存在重复边,不存在顶点到自身的边,则称图 G 为简单图。数据结构中仅讨论简单图。
4)多重图
Q:什么是多重图
A:若图 G 中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则 G 为多重图。多重图的定义和简单图是相对的。
5)完全图
Q:什么是完全图
A:对于无向图,∣E∣ 的取值范围是 0 到 n(n-1)/2 ,有 n(n -1)/2 条边的无向图称为完全图。在完全图中任意两个顶点之间都存在边。对于有向图, |E| 的取值范围是 0 到 n(n-1) ,有 n(n-1) 条弧的有向图称为有向完全图,在有向完全图中任意两个顶点之间都存在方向相反的两条弧。
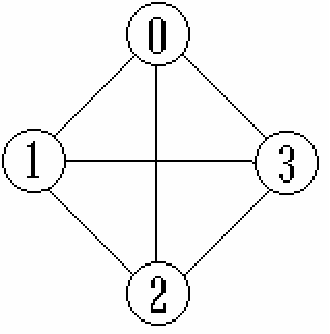
无向完全图
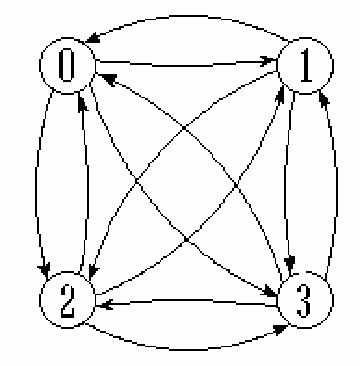
有向完全图
6)子图
Q:什么是子图
A:设有两个图 G=(V, E) 和 G'=(V', E') ,若 V' 是 V 的子集,且 E ′ 是 E 的子集,则称 G ′ 是 G 的子图。若有满足 V(G')= V(G) 的子图 G′,则称其为 G 的生成子图。
**注意:**并非 V 和 E 的任何子集都能构成 G 的子图,因为这样的子集可能不是图,即 E 的子集中的某些边关联的顶点可能不在这个 V 的子集中。
7)连通、连通图和连通分量
在无向图中,若从顶点 v到顶点 w有路径存在,则称 v 和 w 是连通的。
若图 G 中任意两个顶点都是连通的,称图 G 为连通图,否则称为非连通图。
无向图中的极大连通子图称为连通分量。
若一个图有 n 个顶点,并且边数小于 n − 1 ,则此图必是非连通图。
8)强连通图、强连通分量
在有向图中,若从顶点 v 到顶点 w 和从顶点 w 到项点 v 之间都有路径,则称这两个顶点是强连通的。
若图中任何一对顶点都是强连通的,则称此图为强连通图。
有向图中的极大强连通子图称为有向图的强连通分量。
**注意:**强连通图、强连通分量只是针对有向图而言的。一般在无向图中讨论连通性,在有向图中考虑强连通性。
9)顶点的度、入度和出度
无向图:以顶点 i 为端点的边数称为该顶点的度。
有向图:以顶点 i 为终点的入边的数目称为该顶点的入度。以顶点 i 为始点的出边的数目称为该顶点的出度。一个顶点的入度和出度和称为该顶点的度。
10)边的权和网
在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的
权值。这种边上带有权值的图称为
带权图,也称网。
11)生成树、生成森林
连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为 n ,则它的生成树含有 n-1 条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路。在非连通图中,连通分量的生成树构成了非连通图的生成森林。
12)稠密图、稀疏图
边数很少的图称为稀疏图,反之称为稠密图。稀疏和稠密本身是模糊的概念,稀疏图和稠密图常常是相对而言的。一般当图 G 满足 |E| < |V|log|V| 时,可以将 G 视为稀疏图。
13)路径、路径长度和回路
顶点 vp 到顶点 vq 之间的一条路径是指顶点序列 vp,vi1,vi2,...,vim,vq 当然关联的边也可以理解为路径的构成要素。路径上边的数目称为路径长度。第一个顶点和最后一个顶点相同的路径称为回路或环。若一个图有 n 个顶点,并且有大于 n-1 条边,则此图一定有环。

🌺图的存储结构
图的存储必须完整准确的反映顶点集和边集的信息,下面我们介绍两种简单的方法。
🍁邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组 V 存储图中顶点信息,一个二维数组(称为邻接矩阵) A 存储图中的边或弧的信息。
设 G=(V,E) 是具有n个顶点的图,顶点的顺序为(v0,v1 ,… ,vn-1),则G的邻接矩阵A:
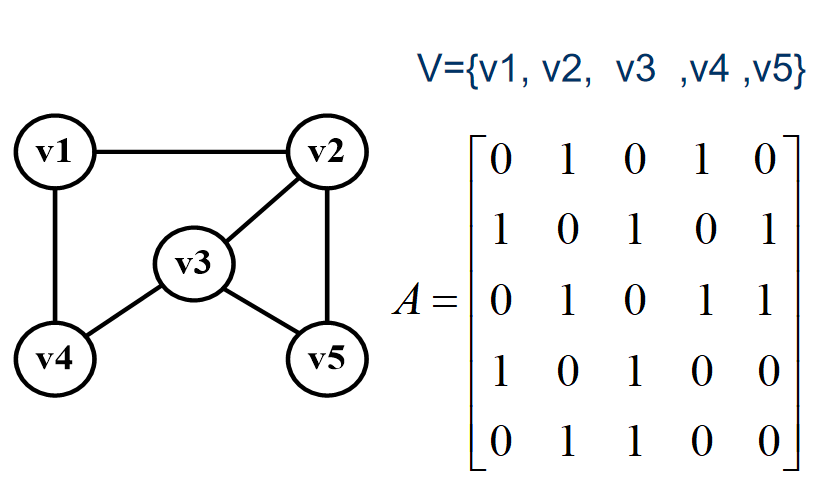
** 下图是一个无向图和它的邻接矩阵:**
** 通过观察不难发现:**
- 1)无向图的邻接矩阵是一个对称矩阵,且主对角线都为 0 。
- 2)我们要知道某个顶点的度,其实就是这个顶点 Vi 在邻接矩阵中第 i 行(或第 i 列)的元素之相。比如顶点 V1 的度就是 0+1+0+1+0=2 。
- 3)求顶点 vi 的所有邻接点就是将矩阵中第 i 行元素扫描一遍, A[i][j] 为 1 就是邻接点。
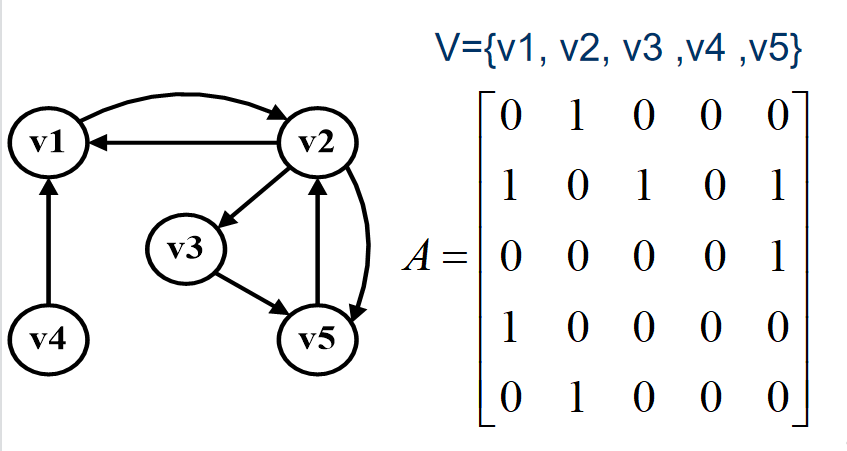
** 下图是一个有向图和它的邻接矩阵:**
** 通过观察不难发现:**
- 1)有向图的邻接矩阵不是一个对称矩阵,且主对角线都为 0 。
- 2)有向图讲究入度与出度,顶点 V1 的入度为 1 ,正好是第 V1 列各数之和。顶点 V1 的出度为 2,即第 V1 行的各数之和。
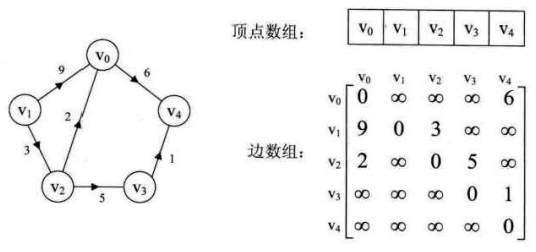
对于带权图来说,若顶点 Vi 和 Vj 之间有边相连,则邻接矩阵中对应项存放着该边对应的权值
** 下图是有向网图和它的邻接矩阵:**
💬 代码演示
通过上文,我们可以定义出邻接矩阵的存储结构:
#define MAXNum 100 //顶点的最大值 typedef char VertexType; //顶点信息为字符类型 typedef struct { VertexType Vex[MAXNum]; //顶点表 int arcs[MAXNum][MAXNum]; //邻接矩阵 int vexnum,arcnum; //顶点数和边数 }MGraph;
🍁邻接表
当一个图为稀疏图时,使用邻接矩阵法显然要浪费大量的存储空间,图的邻接表法结合了顺序存储和链式存储方法,可以大大减少这种不必要的浪费。
邻接表的处理办法:
- 图中顶点用一个一维数组存储,当然也可以用单链表来存储。用数组可以较容易的读取顶点信息,更加方便。另外,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
- 图中每个顶点 vi 的所有邻接点构成一个线性表。由于邻接点的个数不定,所以用单链表存储,无向图称为顶点 vi 的边表,有向图则称为以 vi 为弧尾的出边表。
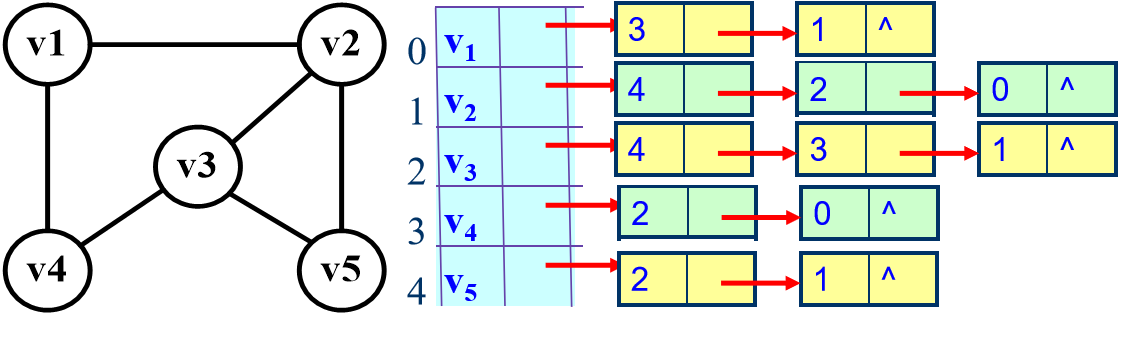
下图是一个无向图的邻接表结构:
邻接表存储的图具有的特点:
- 邻接表表示不唯一。取决于单链表的创建算法和边的输入次序。
- 对于无向图,邻接表的顶点 vi 对应的第i个链表的边结点数目正好是顶点 vi 的度。
- 对于有向图,邻接表的顶点 vi 对应的第 i 个链表的边结点数目仅是顶点 vi 的出度。入度为所有邻接点域为 i 的边结点的数目。
💬 代码演示
#define MAXVEX 100 //图中顶点数目的最大值 typedef char VertexType; typedef int EdgeType; //边表结点 typedef struct EdgeNode{ int adjvex; //该弧所指向的顶点的下标或者位置 EdgeType weight; //权值,对于非网图可以不需要 struct EdgeNode *next; //指向下一个邻接点 }EdgeNode; //顶点表结点 typedef struct VertexNode{ Vertex data; //顶点域,存储顶点信息 EdgeNode *firstedge //边表头指针 }VertexNode, AdjList[MAXVEX]; //邻接表 typedef struct{ AdjList adjList; int numVertexes, numEdges; //图中当前顶点数和边数 }
版权归原作者 锡兰Ceylan_ 所有, 如有侵权,请联系我们删除。