0
0

时间复杂度和空间复杂度

    对于任何一个程序都有好坏、效率高低之分，衡量这些的标准就是“复杂度”，什么是复杂度？

其属于计算机复杂性理论的概念，即表示某个问题消耗时间或空间等资源量多少。

表示方法：

大O渐进表示法：

需要借助代码演示：计算一下这段代码的运行次数？

void func1(int N){
        int count = 0;
        for (int i = 0; i < N ; i++) {
            for (int j = 0; j < N ; j++) {
                count++;
            }
        }
        for (int k = 0; k < 2 * N ; k++) {
            count++;
        } 
        int M = 10;
        while ((M--) > 0) {
            count++;
        } 
        System.out.println(count);
    }

运行次数为：N^{2} + 2 * N + M 次；

大O渐进法规则：

  • 用常数1取代运行时间中的所有加法常数；
  • 只保留最高阶项；
  • 如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶；

那么上面代码的运行次数使用大O渐进法后就变为N^{2}。

为什么要使用渐进法？

  1. 对于常数项：相比于最高阶项，当N的值取无限大时，常数项可以忽略；
  2. 对于低阶项：相比于最高阶项，当N的值取无限大时，其对效率的影响并没有最高阶项的影响大；
  • 综上：对于复杂度，我们往往取其最坏的情况，并去掉那些影响不大的项，当某个算法在最坏的情况下效率在其他算法中还是最高的，那么这样的算法就是最优的。

经典时间复杂度计算：

1.普通单循环体：

循环次数未知：O(N)

  •     F(N) = 2*N + M，系数2和M都省略：

    void func2(int N) {
        int count = 0;
        for (int k = 0; k < 2 * N; k++) {
            count++;
        }
        int M = 10;
        while ((M--) > 0) {
            count++;
        }
        System.out.println(count);
    }

  •     F(N) = N + N = 2*N，系数2省略：

void func3(int N, int M) {
        int count = 0;
        for (int k = 0; k < M; k++) {
            count++;
        } 
        for (int k = 0; k < N ; k++) {
            count++;
        }
        System.out.println(count);
    }

循环次数已知：O(1)

  •      F(N) = 100，已知为100次，视为O(1)

    void func4(int N) {
        int count = 0;
        for (int k = 0; k < 100; k++) {
            count++;
        }
        System.out.println(count);
    }

冒泡排列：O(N^2)

​

 void bubbleSort(int[] array) {
        for (int end = array.length; end > 0; end--) {
            boolean sorted = true;
            for (int i = 1; i < end; i++) {
                if (array[i - 1] > array[i]) {
                    Swap(array, i - 1, i);
                    sorted = false;
                }
            }
            if
            (sorted == true) {
                break;
            }
        }
    }

二分查找：O(logN)

​

   int binarySearch(int[] array, int value) {
        int begin = 0;
        int end = array.length - 1;
        while (begin <= end) {
            int mid = begin + ((end-begin) / 2);
            if (array[mid] < value)
                begin = mid + 1;
            else if (array[mid] > value)
                end = mid - 1;
            else
                return mid;
        }
        return -1;
    }

递归求阶乘：O(N)

​

long factorial(int N) {
        return N < 2 ? N : factorial(N - 1) * N;
    }

递归求斐波那契数：O(2^N)

​

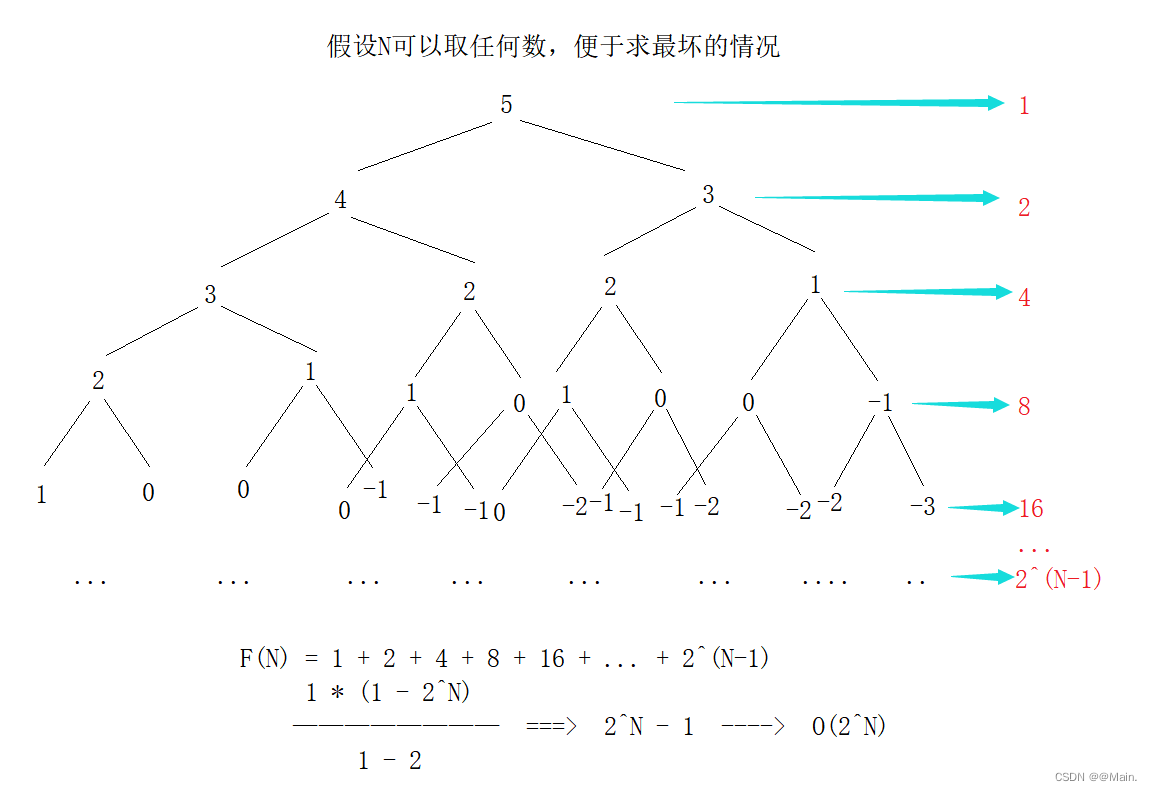
 int fibonacci(int N) {
        return N < 2 ? N : fibonacci(N - 1) + fibonacci(N - 2);
    }

空间复杂度

    空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。

    空间复杂度的计算也并不是计算程序具体占用内存的字节大小，一般用变量的个数来表示，也采取大O渐进法。

经典空间复杂度计算：

冒泡排列：O(1)

形参为数组，只需要为其分配一个有实参传来的地址空间；

sorted在循环体中每次创建使用后又会销毁；

整个程序只使用了有限常数个额外空间，因此为O(1)；

void bubbleSort(int[] array) {
        for (int end = array.length; end > 0; end--) {
            boolean sorted = true;
            for (int i = 1; i < end; i++) {
                if (array[i - 1] > array[i]) {
                    Swap(array, i - 1, i);
                    sorted = false;
                }
            }
            if
            (sorted == true) {
                break;
            }
        }
    }

普通循环求斐波那契数列：O(N)

单看方法内部第一行就为数组开辟了至少N个空间，故为O(N)；

int[] fibonacci(int n) {
        long[] fibArray = new long[n + 1];
        fibArray[0] = 0;
        fibArray[1] = 1;
        for (int i = 2; i <= n; i++) {
            fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
        }
        return fibArray;
    }

二维数组：O(N^2)

​

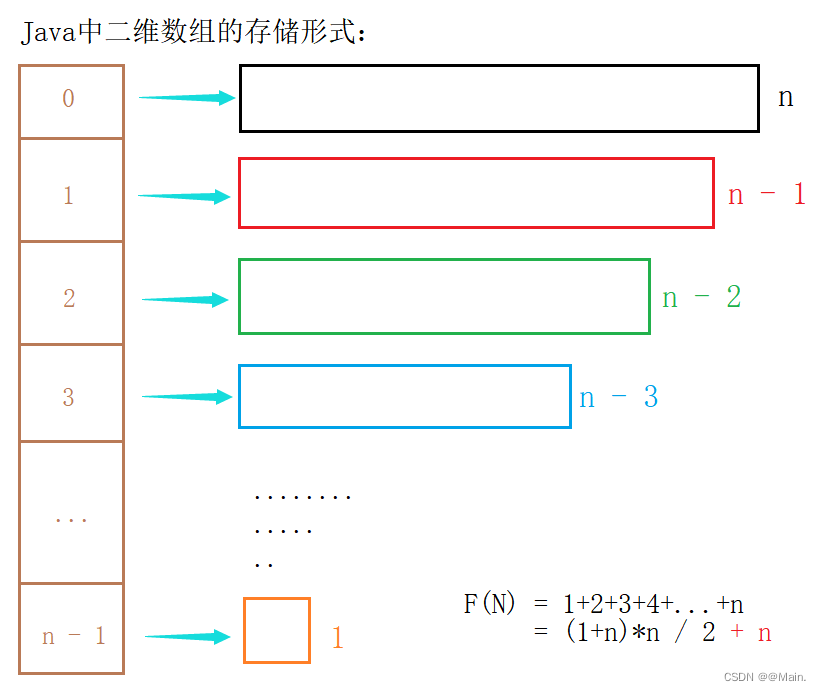
public static int[][] get2Array(int n){
    int[][] array = new int[n][];
    for(int i = 0; i < n; i++) {
        array[i] = new int[n-i];
        n--;
    }

    return array;
}

递归求阶乘：O(N)

​

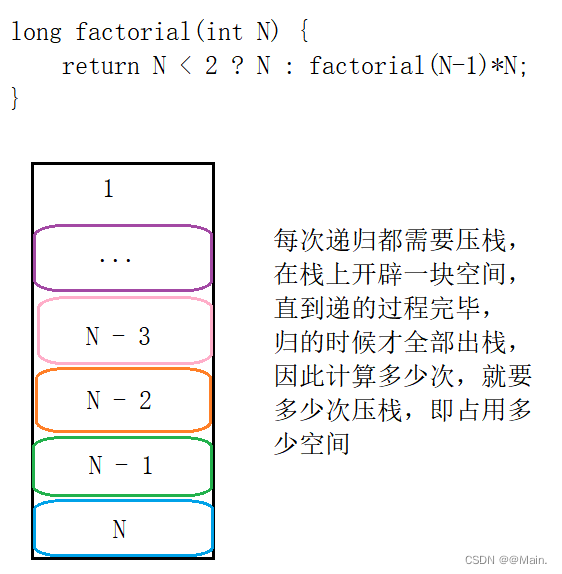
long factorial(int N) {
    return N < 2 ? N : factorial(N-1)*N;
}

递归求斐波那契数列：O(N)

递归过程中，先算Fibonacci(N - 1)这一支，算完后再算fibonacci(N - 2)这一支，两支既然分开算，那么就会两次两次完整的压栈出栈，最坏的情况依然是N次；

 int fibonacci(int N) {
        return N < 2 ? N : fibonacci(N - 1) + fibonacci(N - 2);
    }

经典练习题：

消失的数字

数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗？

注意：本题相对书上原题稍作改动

示例 1：

输入：[3,0,1]
输出：2

示例 2：

输入：[9,6,4,2,3,5,7,0,1]
输出：8

来源：力扣（LeetCode）
链接力扣https://leetcode.cn/problems/missing-number-lcci/

方法一：初始化一个新数组全部元素为-1，将nums中出现过的数字作为下标索引新数组中

class Solution {
    public int missingNumber(int[] nums) {
        int[] temp = new int[nums.length + 1];
        Arrays.fill(temp,-1);
        for(int i = 0;i < nums.length; i++){
            temp[nums[i]] = nums[i];
        }
        for(int i = 0;i < temp.length; i++){
            if(temp[i] == -1){
                return i;
            }
        }
        
        return -1;
    }
}

方法二：先将其原本完整序列两两之间异或一遍，用得到的数再去异或一边给定序列，得到的数就是消失的数字

原理：1. 0异或任何数 = 该数；

       2. 相同数字之间异或 = 0；

class Solution {
    public int missingNumber(int[] nums) {
        int n = 0;
        for (int i = 0; i <= nums.length; i++) {
            n ^= i;
        }

        for(int i = 0;i < nums.length; i++){
            n ^= nums[i];
        }

        return n;
    }
}

方法三：先从0加到n得到sum1，再计算给定序列的和sum2，用sum1 - sum2，即可得到消失的数；

轮转数组

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

来源：力扣（LeetCode）
链接：力扣https://leetcode.cn/problems/rotate-array/

要求复杂度为O(1)：即原地算法

​

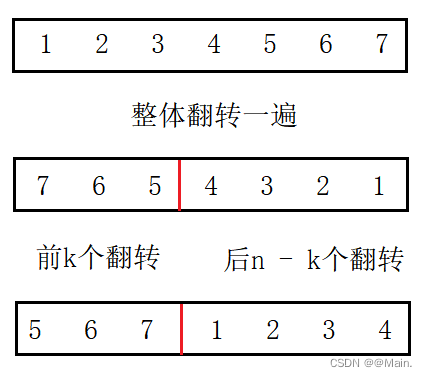
class Solution {
    public void rotate(int[] nums, int k) {
        int left = 0;
        int right = nums.length - 1;
        //数组只有一个元素的情况：
        if(nums.length < 2){
            return;
        }
        //k 大于数组长度的情况：
        if(k > nums.length){
            k %= nums.length;
        }
        //整体翻转
        while(left < right){
            int temp = nums[right];
            nums[right] = nums[left];
            nums[left] = temp;
            left++;
            right--;
        }
        //前 k 个翻转——后 n - k 个翻转
        left = 0;
        right = k - 1;
        while(left < right){
            int temp = nums[right];
            nums[right] = nums[left];
            nums[left] = temp;
            left++;
            right--;
        }
        left = k;
        right = nums.length - 1;
        while(left < right){
            int temp = nums[right];
            nums[right] = nums[left];
            nums[left] = temp;
            left++;
            right--;
        }
    }
}

寻找数组中心下标

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

示例 1：

输入：nums = [1, 7, 3, 6, 5, 6]
输出：3
解释：
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ，
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ，二者相等。
示例 2：

输入：nums = [1, 2, 3]
输出：-1
解释：
数组中不存在满足此条件的中心下标。
示例 3：

输入：nums = [2, 1, -1]
输出：0
解释：
中心下标是 0 。
左侧数之和 sum = 0 ，（下标 0 左侧不存在元素），
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。

来源：力扣（LeetCode）
链接：力扣https://leetcode.cn/problems/find-pivot-index/

这一题要求转化为数学公式即为：

X + a = Y + a ; ==== > X = Y；

故我们可以理解为：左边的和与右边的和相等时，若它们有公共的一个数，这个数的下标就是中心下标；

class Solution {
    public int pivotIndex(int[] nums) {
        //将左右和的公用部分找出来就是中心坐标
        int sum = 0;
        int leftSum = 0;
        int rightSum = 0;
        for(int i = 0;i < nums.length; i++){
            sum += nums[i];
        }
        for(int i = 0;i < nums.length; i++){
            leftSum += nums[i];
            rightSum = sum - leftSum + nums[i];
            if(leftSum == rightSum){
                return i;
            }
        }

        return -1;

    }
}
标签： java 数据库 数据结构
本文转载自: https://blog.csdn.net/m0_65190367/article/details/126737490
版权归原作者 @Main. 所有， 如有侵权，请联系我们删除。
登录后发布评论

“时间复杂度和空间复杂度”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

[CKS] CIS基准测试，修复kubelet和etcd不安全项

AOSP Settings 单元测试 | 如何运行Android 应用测试？（单元测试&仪器测试）

Visual Studio 2022工作原理及相关配置参数（干货满满）——C++

【手把手教你】heidisql安装与配置全攻略 - 开源数据库管理工具入门指南

【成神之路】Ambari实战-050-UI-如何通过配置修改ambari样式

前端必知必会-Bootstrap 5 导航栏Navbars

【Spring】RESTful设计风格

文章导航