1.启发式搜索方法与第 2 章讨论的搜索方法有什么区别?
在第二章的学习中我们学习了盲目搜索算法。
启发式搜索方法和盲目搜索方法的区别在于其搜索策略的不同。盲目搜索方法是一种无法预测搜索方向的搜索方法,它只是简单地按照某种规则或算法进行搜索,没有考虑到问题的特性和目标状态的位置。而启发式搜索方法则是一种根据问题的特性和目标状态的位置来指导搜索方向的搜索方法,它通过一些启发函数或启发规则来评估每个可能的移动,并选择最有希望达到目标状态的移动。因此,启发式搜索方法通常比盲目搜索方法更高效,能够更快地找到问题的解决方案。
(a)给出启发式搜索的 3 种定义。
1.启发式搜索是一种基于问题特性和目标状态的位置来指导搜索方向的搜索方法,通过启发函数或规则来评估每个可能的移动,并选择最有希望达到目标状态的移动。
2.启发式搜索是一种利用领域特定的信息来指导搜索过程的方法,以提高搜索效率和减少搜索空间。
3.启发式搜索是一种通过估计每个搜索节点与目标状态的距离或代价来选择最有希望的节点进行扩展的搜索方法,以加速问题解决过程。
(b)给出将启发式信息添加到搜索中的 3 种方式。
1.启发函数:通过定义一个启发函数来评估每个可能的移动或状态,以指导搜索方向。启发函数可以根据问题的特性和目标状态的位置来估计每个状态到目标状态的距离或代价,从而选择最有希望的移动或状态进行扩展。
2.剪枝策略:利用启发式信息来进行剪枝,即在搜索过程中根据启发式信息提前排除一些不太可能达到目标状态的状态或移动,从而减少搜索空间和提高搜索效率。
3.搜索方向优先级:根据启发式信息对搜索方向进行优先级排序,使得具有更高启发式价值的搜索方向先被探索,从而更快地找到问题的解决方案。
2.为什么爬山法可以归类为贪心算法?
因为爬山法在每一步都会选择当前状态中具有最大启发式价值的邻居作为下一步的移动方向,而不考虑长远的后果。这种策略符合贪心算法的特点,即每一步都做出当前最优的选择,而不考虑整体的最优解。爬山法只关注局部最优解,而不会全局考虑,这与贪心算法的思想相吻合。因此,爬山法可以被归类为贪心算法。
3.最陡爬山法如何提供最优解?
最陡爬山法可以提供局部最优解,但不一定能够达到全局最优解。
最陡爬山法容易陷入局部最优解,因为它只考虑当前解的相邻解中评估值最大的那个,而没有考虑其他可能更优的解。如果在搜索过程中,当前解的相邻解评估值最大的解都不比当前解更优,那么最陡爬山法会停止搜索,无法达到全局最优解。
为了使最陡爬山法提供最优解,可以采用一些改进策略,如随机重启、模拟退火等来增加算法的全局搜索能力。另外,结合其他搜索算法,如遗传算法、模拟退火算法等,也可以提高最陡爬山法的全局搜索能力,从而更有可能找到全局最优解。
4.为什么最佳优先搜索比爬山法更有效?
因此,最佳优先搜索相对于爬山法来说,更加有效是因为它具有更强的全局搜索能力和更好的节点扩展策略。
最佳优先搜索比爬山法更有效的主要原因在于其全局搜索能力更强。最佳优先搜索考虑了每个节点到目标节点的启发式估计值,并根据这些估计值来选择下一个扩展的节点,从而更有可能找到全局最优解。相比之下,爬山法只是简单地选择具有最大启发式价值的邻居作为下一步的移动方向,容易陷入局部最优解而无法跳出。
此外,最佳优先搜索采用了优先级队列来管理待扩展的节点,可以保证总是先扩展具有最小启发式估计值的节点,这样可以更快地找到最优解。而爬山法没有使用优先级队列,因此可能会在局部最优解周围徘徊,无法有效地向全局最优解前进。
5.解释集束搜索的工作原理。
集束搜索(Beam Search)是一种启发式搜索算法,通常用于在大规模搜索空间中寻找近似最优解。其工作原理如下:
- 初始化:从初始状态出发,生成若干个候选解(也称为束),每个候选解对应一个搜索路径。这些候选解通常是根据某种启发式方法生成的。
- 扩展:对每个候选解,根据特定的扩展策略,生成其相邻的候选解。这些相邻候选解可能是通过对当前候选解进行状态扩展、移动、变换等方式得到的。
- 评估:对于生成的相邻候选解,通过某种评估函数或启发式方法对其进行评估,得到其质量或优劣程度。
- 选择:根据评估结果,保留质量较高的一部分候选解,并丢弃质量较低的候选解。这一步也称为剪枝操作。
- 终止条件:重复进行扩展和选择步骤,直至满足终止条件。终止条件可以是达到最大迭代次数、找到满足特定条件的解、或者其他预先设定的条件。
通过这样的迭代过程,集束搜索可以在大规模搜索空间中快速寻找到较优的解。由于集束搜索同时维护多个候选解,因此具有一定的并行性,能够在一定程度上避免陷入局部最优解。然而,集束搜索也可能无法保证找到全局最优解,因为在剪枝操作中可能丢弃了包含全局最优解的候选解。
6.启发式方法的可接受性(admissible)是什么意思?
启发式方法的可接受性(admissibility)是指启发函数对于每个节点的评估值都不会高估目标节点的实际代价。换句话说,可接受的启发函数不会导致搜索算法找到比最优解更差的解。
(a)可接受性与单调性有什么关系?
可接受性与单调性是紧密相关的概念。单调性是指对于任意两个相邻节点,如果从一个节点到另一个节点的实际代价是非负的,那么启发函数的评估值应该满足单调性。具体来说,如果一个启发函数是单调的,那么对于任意节点 n 和它的相邻节点 n^,满足 h(n) ≤ c(n, n^) + h(n^),其中 h(n) 表示启发函数对节点 n 的评估值,c(n, n^) 表示从节点 n 到节点 n^ 的实际代价。单调性是保证可接受性的重要条件。
(b)可以只有单调性,而不需要可接受性吗?解释原因。
在一些情况下,我们可以只有单调性而不需要可接受性。单调的启发函数可以帮助选择更好的路径,但并不能保证找到最优解。如果只有单调性而没有可接受性,搜索算法可能会停在一个次优解上,而无法达到全局最优解。通过引入可接受性,我们可以更有信心地选择启发函数评估值较小的节点,并继续搜索更有希望的解。因此,可接受性是为了提高搜索算法的性能和保证找到最优解而重要的概念。
7.一种启发式方法比另一种启发式方法具有更多的信息,这句话的意思是什么?
这句话的意思是,一种启发式方法相对于另一种启发式方法在提供有关搜索空间的信息方面更为丰富。
在搜索算法中,启发式方法用于对搜索空间中的状态进行评估,以指导搜索方向并尽可能快速地找到最优解。如果一种启发式方法比另一种启发式方法具有更多的信息,意味着它能够更准确地估计状态之间的代价或价值,或者提供了更多关于状态之间关系的信息。
具有更多信息的启发式方法通常能够更好地引导搜索算法朝着最优解的方向前进,从而更有可能找到更优的解。然而,启发式方法信息的丰富程度并不总是与搜索算法的性能成正比,因为信息的利用方式和搜索算法的设计也会影响最终的搜索效果。
因此,一种启发式方法比另一种启发式方法具有更多信息,意味着它在评估搜索空间状态时能够提供更多、更准确的信息,从而有望在搜索过程中更有效地指导算法朝着最优解前进。
8.分支定界法背后的思想是什么?
分支定界法(Branch and Bound)是一种用于求解组合优化问题的算法,其背后的思想是通过对搜索空间进行分支和限界,以找到最优解或者满足特定条件的解。
该算法的基本思想包括以下几个步骤:
- 分支:从初始状态出发,将搜索空间分解为若干个子空间,每个子空间对应于一个决策变量的取值或者一个选择。这样,原始问题就被分解为多个子问题。
- 限界:对每个子空间进行评估,计算其上界和下界。上界是指该子空间中可能的最优解的上限值,下界是指该子空间中可能的最优解的下限值。通过比较上界和下界,可以确定是否需要进一步探索该子空间,或者可以将该子空间剪枝掉。
- 回溯:当找到一个更好的解或者确定某个子空间不可能包含更优解时,可以回溯到之前的状态,继续探索其他子空间。
通过不断地分支和限界,分支定界法能够逐步缩小搜索空间,直到找到最优解或者满足特定条件的解。这种方法在求解组合优化问题(如旅行商问题、0-1背包问题等)时非常有效,因为它能够避免对整个搜索空间进行穷举搜索,从而减少搜索时间和空间复杂度。
9.请解释低估可能会得到更好的解的原因。
低估可能会导致更好的解的原因有以下几点:
- 剪枝效果:低估的启发式函数会导致对搜索空间中状态的下界进行低估,这样会减少剪枝的数量,使得算法在搜索过程中能够保留更多的备选解。这样在搜索过程中保留更多的备选解,有助于找到更好的解。
- 探索更广的空间:低估的启发式函数可能会导致算法在搜索过程中更多地探索可能的状态空间,因为它会认为某些实际上并不是那么有希望的状态也是值得考虑的。这种广泛的探索可能会使算法找到更优的解,而不会过早地停止搜索。
- 更快的收敛:低估的启发式函数有助于使算法更快地收敛到最优解附近,因为它会更积极地探索可能的状态空间,从而更快地找到更优的解。
10.关于动态规划:
(a)动态规划的概念是什么?
动态规划是一种通过将问题分解为重叠的子问题并利用子问题的最优解来求解原始问题的技术。它通常用于解决具有重叠子问题和最优子结构特性的问题。动态规划将问题划分为多个步骤或阶段,并以递推的方式从较小的子问题开始求解,不断利用已经求解过的子问题的解来构造更大的问题的解。通过将复杂的问题拆分为小的可解决子问题,并将它们的解缓存起来,动态规划能够有效地避免重复计算,提高算法的效率。
(b)描述最优性原理。
最优性原理是动态规划的一个重要概念。它表述了这样的一种性质:一个问题的最优解可以通过其子问题的最优解来构造。具体来说,如果一个问题的最优解包含了子问题的最优解,那么我们可以在求解问题时利用这个性质,将问题分解为子问题,并利用子问题的最优解递推出原问题的最优解。最优性原理给动态规划算法提供了一种有效的求解思路和算法结构。
最优性原理的核心思想是利用子问题的最优解构造出更大问题的最优解。这意味着我们可以通过首先找到子问题的最优解,然后利用这些最优解在问题规模增大的过程中递推到原始问题的最优解。通过这种方式,动态规划能够通过重复利用子问题的最优解来求解整个问题,避免了重复计算,提高了算法的效率。
11.为什么 A 算法比使用低估计启发值的分支定界法或使用动态规划的分支定界法更好?*
①更高效的搜索:A算法结合了启发式搜索和最佳优先搜索的特点,能够在搜索过程中更加智能地选择下一步要探索的节点,因此通常能够更快地找到最优解。相比之下,分支定界法通常需要遍历整个状态空间,而动态规划的分支定界法可能需要不断地重复计算子问题的解,因此在搜索效率上不如A算法。
② 更好的解的质量:A算法通过启发式函数来估计每个节点到目标的代价,这使得算法能够更加聪明地选择下一步要探索的节点,从而通常能够找到更好的解。相比之下,使用低估启发式值的分支定界法可能会错过一些更优的解,而动态规划的分支定界法可能会受限于状态空间的大小和重复计算的问题,导致找到的解质量不如A算法。
③ 适用范围更广:A算法在解决许多实际问题时表现良好,例如路径规划、游戏搜索等。它的启发式搜索能力和最佳优先搜索的特点使得它适用于多种问题。相比之下,分支定界法和动态规划的分支定界法可能更适用于某些特定类型的问题,且在某些情况下可能不如A算法。
12.解释约束满足搜索背后的思想,以及它是如何应用于“驴滑块”拼图问题的。
约束满足搜索是一种用于解决满足一组约束条件的问题的搜索方法。它的基本思想是通过搜索空间中的状态,并在搜索过程中逐步满足问题的约束条件,直到找到满足所有约束条件的解。
在约束满足搜索中,通常会使用启发式搜索的方法,通过评估当前状态的约束违反程度或者与目标状态的距离来指导搜索的方向。这样可以在搜索过程中更加智能地选择下一步要探索的状态,从而更快地找到满足所有约束条件的解。
在"驴滑块"拼图问题中,约束满足搜索可以被应用于寻找一种移动序列,使得初始状态中的滑块按照规定的拼图规则移动到目标状态。在这个问题中,约束通常包括滑块的移动规则、目标状态等。
具体来说,约束满足搜索可以通过如下步骤应用于"驴滑块"拼图问题:
①定义状态空间:将每个可能的拼图状态表示为搜索空间中的一个状态。
②定义约束条件:将滑块的移动规则、目标状态等作为问题的约束条件。
③ 启发式搜索:使用启发式搜索的方法,比如A*算法,通过评估当前状态距离目标状态的距离来指导搜索的方向。
④逐步满足约束:在搜索过程中,逐步满足问题的约束条件,直到找到一个满足所有约束条件的解,即找到了从初始状态到目标状态的移动序列。
13.解释如何用与或树来划分搜索问题。
使用与或树来划分搜索问题是一种常见的方法,可以帮助我们理清问题的结构和可能的解决方案。
首先,我们将问题分解为多个子问题,并将这些子问题表示为树的节点。与节点表示需要同时满足所有子节点的条件,或节点表示至少有一个子节点需要满足条件。
然后,我们在树的每个节点上标记是与节点还是或节点,并将可能的解决方案作为子节点连接到对应的节点上。
通过搜索与或树,我们可以逐步深入到各个分支中,以寻找满足条件的解决方案。这种方法有助于理解问题的结构、约束条件和可能的解决方案,从而更有效地进行搜索。
14.描述双向搜索的工作原理。
双向搜索是一种搜索算法,它同时从起始状态和目标状态开始搜索,直到两个搜索方向相遇。具体工作原理如下:
- 从起始状态和目标状态分别开始搜索,使用广度优先搜索或其他搜索算法向外扩展。
- 在搜索过程中,记录已经访问的状态,并检查两个搜索方向是否相遇。如果相遇,则找到了解决方案。
- 如果两个搜索方向相遇,则可以通过记录相遇点的路径,找到从起始状态到目标状态的最短路径。
(a)它与本章中讨论的其他技术有什么不同?
与本章学习的知情搜索、最佳优先搜索和集束搜索等相比,双向搜索的不同之处在于:它从起始状态和目标状态同时进行扩展,而其他知情搜索算法只从一个方向进行扩展。最佳优先搜索(Best-First Search)根据启发式函数的值来选择下一个要扩展的节点,而双向搜索并不直接依赖于启发式函数。集束搜索(Beam Search)和双向搜索类似,但集束搜索通常只从一个方向进行扩展,并且限制了搜索队列的大小。
(b)描述边界问题和导弹隐喻的含义。
边界问题是指在决策制定中需要考虑的各种限制和条件,而导弹隐喻则是一种描述决策制定中需要权衡的多种因素的比喻。导弹隐喻指出,在制定决策时,需要平衡不同的目标和因素,就像调整导弹的飞行轨迹一样,需要考虑各种限制和条件。
(c)什么是波形规整算法?
波形规整算法是一种用于解决拼图问题的启发式搜索算法。它通过模拟水波扩散的过程来搜索拼图的解决方案。在每一步中,波形规整算法选择一个最有希望的移动,以逐步接近目标状态。这种算法在拼图问题中通常能够找到较优的解决方案。
练习题
1.给出 3 个启发式方法的例子,解释它们如何在以下情景中发挥重要作用。
(a)在日常生活中。
"分配注意力" 启发式:在处理多个任务时,优先处理最紧急或最重要的任务,以确保高效和优先完成重要工作。
"避免后悔" 启发式:在做决策时,考虑未来可能的遗憾和后果,选择能够最大程度避免后悔的选项。
"顺应习惯" 启发式:根据已经建立的良好习惯和惯例进行决策,减少不必要的思考和时间浪费。
(b)在面对某种挑战时的问题求解过程中。
"试错" 启发式:通过尝试不同的策略或方法,并从错误中学习,逐步找到解决问题的有效途径。
"拆分子问题" 启发式:将复杂的问题分解为更小的子问题,逐个解决每个子问题,从而使问题求解更加可行和高效。
"模仿他人" 启发式:在面对陌生问题时,观察和学习他人是如何解决类似问题的,以借鉴其经验和方法,加速问题求解过程。
2.解释爬山法被归类为“贪心算法”的原因。
在讨论题中我们说过,因为爬山法在每一步都会选择当前状态中具有最大启发式价值的邻居作为下一步的移动方向,而不考虑长远的后果。这种策略符合贪心算法的特点,即每一步都做出当前最优的选择,而不考虑整体的最优解。爬山法只关注局部最优解,而不会全局考虑,这与贪心算法的思想相吻合。因此,爬山法可以被归类为贪心算法。
(a)描述你知道的其他一些“贪心”算法。
最小生成树算法(Minimum Spanning Tree, MST):以图为基础的贪心算法,用于找到连接所有节点的最小成本树。算法每次选择具有最小权重的边,直到所有节点都被连接。
最短路径算法(Shortest Path):用于找到两个节点之间最短路径的算法。常见的贪心算法包括Dijkstra算法和Bellman-Ford算法,它们根据当前已知的最短路径信息,每次选择具有最小权重的边来更新路径。
部分背包问题(Fractional Knapsack Problem):用于解决在有限容量下选择物品以获取最大价值的问题。贪心算法每次选择单位价值最高的物品,直到容量被占满。
(b)最陡爬山法是如何改进爬山法的?最佳优先搜索是如何改进爬山法的?
最陡爬山法通过考虑所有邻居节点中具有最小代价的节点进行移动,而不是简单地选择第一个遇到的比当前节点更优的节点。这样可以更有效地朝着最优解移动,避免了爬山法可能陷入局部最优解的问题。
最佳优先搜索使用启发式函数来评估节点的优先级,并选择优先级最高的节点进行扩展。这样可以更加智能地选择下一个节点,并且能够在搜索过程中动态地调整搜索方向,从而更可能找到全局最优解,而不是陷入局部最优解。
3.给出一个未在本章中提及的可接受的启发式方法,解决 3 拼图问题。
"不匹配数量" 启发式方法:计算每个拼图块当前位置与目标位置之间不匹配的数量,选择具有最少不匹配数量的拼图块进行移动。
(a)采用启发式方法执行 A 搜索,求解本章中提出的拼图实例。*
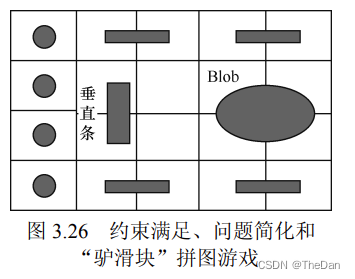
本章提出了“驴滑块”拼图游戏,所以在“驴滑块”拼图游戏中, 给出我的解题思路:
定义状态空间:将每个可能的游戏状态表示为一个节点,节点之间的转移关系表示为边。
定义启发式函数:为了估计从当前状态到目标状态的代价,需要定义一个启发式函数来评估每个状态的优先级,通常使用曼哈顿距离或者错误放置的方块数量作为启发式函数。
初始化搜索:将起始状态加入到搜索队列中,并初始化一个空的已访问状态集合。
进行搜索:从搜索队列中选择一个状态,计算其邻居状态,并根据启发式函数评估每个邻居状态的优先级,然后将它们加入到搜索队列中。
重复步骤4,直到找到目标状态或者搜索队列为空。
返回最优解:如果找到目标状态,根据搜索路径回溯得到最优解。
(b)你提出的启发式方法是否比本章提出的两种启发式方法拥有更多的信息?
"不匹配数量" 启发式方法相比于分支定界法和低估计值的分支定界法,提供的信息较少。
在拼图问题中,"不匹配数量" 启发式方法计算每个拼图块当前位置与目标位置之间的不匹配数量,选择具有最少不匹配数量的拼图块进行移动。这种方法只关注正确位置和当前位置之间的不匹配数量,没有考虑拼图块之间的相对位置和正确的拼图顺序。
4.关于启发式方法,请完成以下练习。
(a)为传教士与野人问题建议一个可接受的启发值,这个启发值应该足够健壮,从而避免 不安全的状态。
对于传教士与野人问题,一个可接受的启发值是将剩余的传教士和野人都放到一个岸边,然后计算从当前状态到目标状态的最小移动步数。这个启发值应该足够健壮,因为它可以避免不安全的状态,即在任何时候都不会有野人数量超过传教士数量的情况发生。这种启发式函数可以有效地指导A*搜索算法朝着最优解前进,同时避免探索不安全的状态。
(b)你的启发式方法能够提供足够的信息,以明显地减少 A 算法所要探索的库吗?*
我的启发式方法可以提供足够的信息,以明显地减少A算法所要探索的空间。通过使用上述提到的启发式函数,A算法可以更加聪明地选择下一个状态进行扩展,从而减少搜索空间。由于启发式函数提供了对目标状态的估计代价,A*算法可以更快地找到最优解,因为它可以优先探索具有更有希望的状态。
** 5.关于启发值,请完成以下练习。**
(a)提供适用于图形着色的启发值。
使用贪婪着色算法,并将各个序号依次标号1~7
- 从顶点 V1 开始,将其着为红色。
- 移至未着色的顶点 V2,并将其着为蓝色(因为它不与任何红色顶点相邻)。
- 接下来选择顶点 V3。由于它与 V2 相邻,因此不能将其着为蓝色。将其着为绿色。
- 对于顶点 V4,将其着为红色,因为它既不与 V1 相邻,也没有其他与红色相邻的顶点。
- 顶点 V5 与 V2 和 V3 相邻,它们分别为蓝色和绿色,因此可以将其着为红色。
- 顶点 V6 可以着为蓝色,因为它只与 V2 相邻,而且由于 V7 尚未着色,没有冲突。
- 最后,顶点 V7 可以着为绿色,因为它只与 V1 和 V6 相邻,它们分别为红色和蓝色。
(b)采用你的启发值找到图 2.41 中的着色数。
3种 ,红和蓝和绿。

6.思考下列 n 皇后问题的变体。 在一个 n×n 的棋盘上,如果一些会被皇后攻击的方块受到兵的阻碍,有超过 n 个皇后可以 放在除去“兵”之外剩余的部分棋盘中吗?例如,如果 5 个兵被添加到一个 3×3 的棋盘上,那 么这个棋盘上可以摆放 4 个互相不攻击的皇后吗?(见图 3.30)
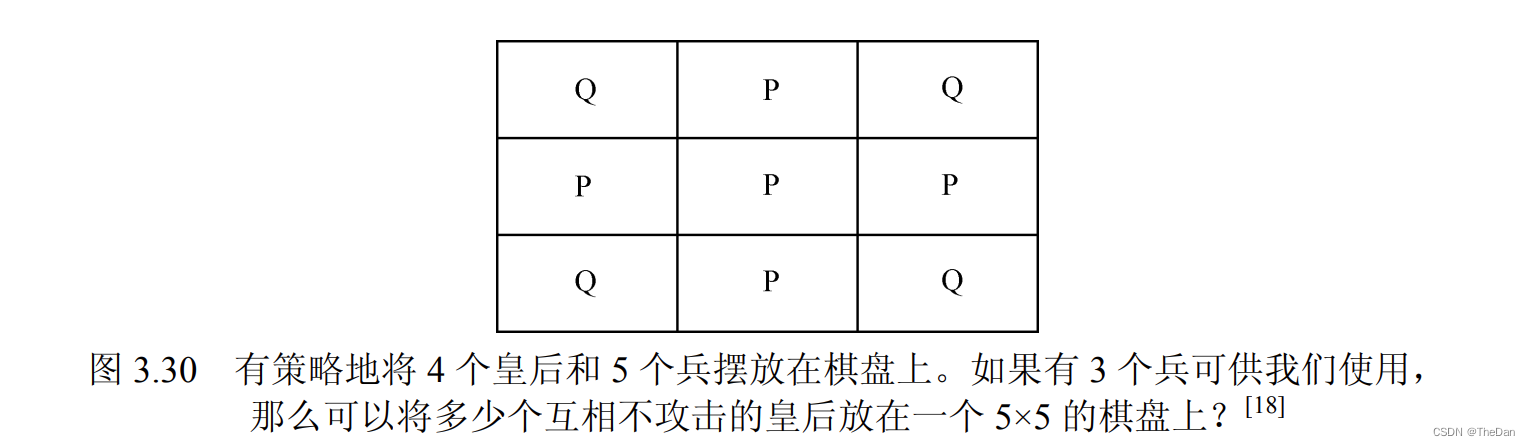
在一个 3x3 的棋盘上,无法摆放4个互相不攻击的皇后。在国际象棋中,皇后可以沿着横、竖、斜线上的任意方向移动,因此在一个 3x3 的棋盘上,任何一个位置放置皇后都会控制大部分的棋盘,导致其他的皇后无法摆放在不受攻击的位置上。因此,图中展示的棋盘上的4个皇后并不满足互相不攻击的条件。
7.在图 3.31 中,用“普通”分支定界法和动态规划的分支定界法,从起始节点 S 行进到目 标节点 G。当所有其他条件都一样时,按照字母顺序探索节点。

图(a)中‘普通’分支定界法的顺序为 S,C,F,S,B,A,D,C,E,F,G动态规划为S,C,F,G
图(b)中‘普通’分支定界法的顺序为S,C,D,E,B,A,C,D,G动态规划为S,C,D,G
当然在‘普通’分支定界法中,我们忽略了进入死循环的可能
8.关于启发式方法,请完成以下练习。
(a)制定可接受的启发式方法来解决第 2 章(见练习 13)中的迷宫问题。
使用曼哈顿距离作为启发式函数,它可以估计从当前位置到目标位置(出口)的成本。A* 搜索算法需要计算每个节点的代价,并根据启发式函数进行搜索。
(b)采用你的启发式方法执行 A* 搜索,解决这个问题。
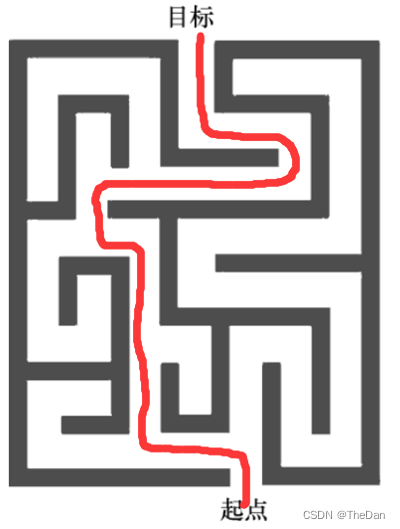
9.关于启发式方法,请完成以下操作。
(a)为水壶问题提出一个可接受的启发式方法。
我们可以使用基于状态的启发式,通过使用水壶A和水壶B当前的水量与目标水量之间的差异作为启发式估计值。即启发式值为|当前的水量-目标水量|。
(b)采用你的启发式方法执行 A 搜索,解决第 1 章中提出的问题实例。*
定义初始状态为(A, B),表示水壶A和B中的水量为0。
定义目标状态为(A, 12)或(B, 12),即要求量出12升的水。
(0, 0) 启发式值:|0-12| = 12
(8, 0) 启发式值:|8-12| = 4
(0, 8) 启发式值:|8-12| = 4
(8, 8) 启发式值:|16-12| = 4
(0, 4) 启发式值:|4-12| = 8
(8, 4) 启发式值:|12-12| = 0
(4, 0) 启发式值:|4-12| = 8
(4, 12) 启发式值:|16-12| = 4
(0, 12) 启发式值:|12-12| = 0
求得(0,12)即为量出的12升水
10.在第 2 章中,我们提出了骑士之旅问题。其中,棋盘上的马访问了 n×n 棋盘上的每一 个方块。这个挑战一开始会在完整的 8×8 棋盘上给定一个源方块[比如方块(1,1)],目标是找 到移动序列,该序列会访问棋盘上的每个方块,每个方块都会被访问且仅仅被访问一次,在最 后一次移动中,马回到源方块。
(a)从方块(1,1)开始,尝试解决骑士之旅问题。(提示:对于这个版本的骑士之旅问题, 你可能会发现需要大量内存来解决。因此,你可能需要确定一个启发式方法,以帮助引导搜索 过程)
(b)尝试找到一种启发式方法,它能帮助初次求解器找到正确解。
11.编写一个程序,在图 3.17 中应用本章描述的主要启发式搜索算法,比如爬山法、集束 搜索、最佳优先搜索、带有或不带有低估计值的分支定界法以及 A 算法等等。*
下面是一个示例程序,展示如何应用A*算法在分支定界法中进行启发式搜索。
class Node:
def __init__(self, state, path, cost):
self.state = state # 当前状态
self.path = path # 当前路径
self.cost = cost # 当前路径的总成本
def B_B_Estimate(Root_Node, Goal):
queue = [Root_Node] # 创建队列
while queue:
G = queue.pop(0) # 从队列中取出节点
if G.state == Goal:
return G.path # 如果找到目标状态,则返回路径
else:
# 扩展节点生成子节点
children = generate_children(G)
# 在添加到队列之前,进行启发式估计值排序
for child in children:
child.cost += heuristic(child.state, Goal)
queue.extend(children)
queue.sort(key=lambda x: x.cost)
return None # 如果没有找到解,则返回空
def generate_children(node):
# 生成当前节点的所有子节点
children = []
# TODO: 根据状态转移规则生成子节点
return children
def heuristic(state, goal):
# 启发式估计函数,计算当前状态到目标状态的估计成本
# 具体估计方法根据实际问题自行定义
# 返回值越小表示距离目标越近
return 0
# 示例用法
Root_Node = Node(start_state, [start_state], 0)
Goal = target_state
result = B_B_Estimate(Root_Node, Goal)
if result:
print("Found path:", result)
else:
print("No path found")
在示例代码中,我们在 B_B_Estimate 函数中应用了 A* 算法来作为启发式搜索的策略。在生成节点的子节点时,我们根据启发式函数 heuristic 计算每个子节点的启发式估计值,并将其加到当前路径成本上。然后,我们将子节点加入队列,并按照路径成本进行排序,以便选择具有最小成本的节点进行扩展。
12.在第 2 章中,我们提出了 n 皇后问题。编写一个程序来解决 8 皇后问题,在这个问题 中,一旦放置某个皇后,就考虑应用移除任何受到攻击的行和列的约束条件。
def solve_n_queens(n):
board = [[0 for _ in range(n)] for _ in range(n)] # 初始化棋盘
solutions = [] # 存储所有解
def is_safe(board, row, col):
# 检查当前位置是否安全
# 检查同一列上是否有其他皇后
for i in range(row):
if board[i][col] == 1:
return False
# 检查左上到右下的对角线上是否有其他皇后
i = row - 1
j = col - 1
while i >= 0 and j >= 0:
if board[i][j] == 1:
return False
i -= 1
j -= 1
# 检查右上到左下的对角线上是否有其他皇后
i = row - 1
j = col + 1
while i >= 0 and j < n:
if board[i][j] == 1:
return False
i -= 1
j += 1
return True
def backtrack(row):
if row == n:
# 找到一个解
solution = []
for i in range(n):
row_str = ''.join(['Q' if cell == 1 else '.' for cell in board[i]])
solution.append(row_str)
solutions.append(solution)
return
for col in range(n):
if is_safe(board, row, col):
board[row][col] = 1 # 放置皇后
backtrack(row + 1) # 继续下一行的放置
board[row][col] = 0 # 回溯,撤销放置的皇后
# 从第一行开始回溯放置
backtrack(0)
return solutions
# 解决 8 皇后问题
solutions = solve_n_queens(8)
# 输出所有解
for sol in solutions:
for row in sol:
print(row)
print("---------")
这个程序使用回溯法来解决8皇后问题。我们定义了一个is_safe函数来检查当前位置是否安全.
13.对于骑士之旅问题的 64 次移动的解,在某一点上,必须放弃你在练习 10.b 中所要确定 的启发式方法。尝试确定该点。
如果是找放弃的点就是使用使用蒙特卡洛方法吧,这个我没有搞懂题是什么意思。
14.求解“驴滑块”拼图问题(见图 3.26),至少需要 81 次移动。考虑可以应用的子目标 来求这个解。
我们可以考虑以下子目标来求解至少需要 81 次移动的解:
- 将数字按照正确的顺序排列:将数字 1 到 15 按照正确的顺序排列在拼图板上。
- 移动空格:通过移动空格,将数字逐步移动到正确的位置。
- 减少冲突:尽量减少数字之间的冲突,即尽量减少需要打乱已经排好顺序的数字。
版权归原作者 TheDan 所有, 如有侵权,请联系我们删除。