数据结构 Java数据结构 ---- 堆(优先级队列)

文章目录

堆(优先级队列)

1.二叉树的顺序存储

1.1 存储方式

使用数组保存二叉树结构，方式即将二叉树用层序遍历方式放入数组中。
一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。
这种方式的主要用法就是堆的表示。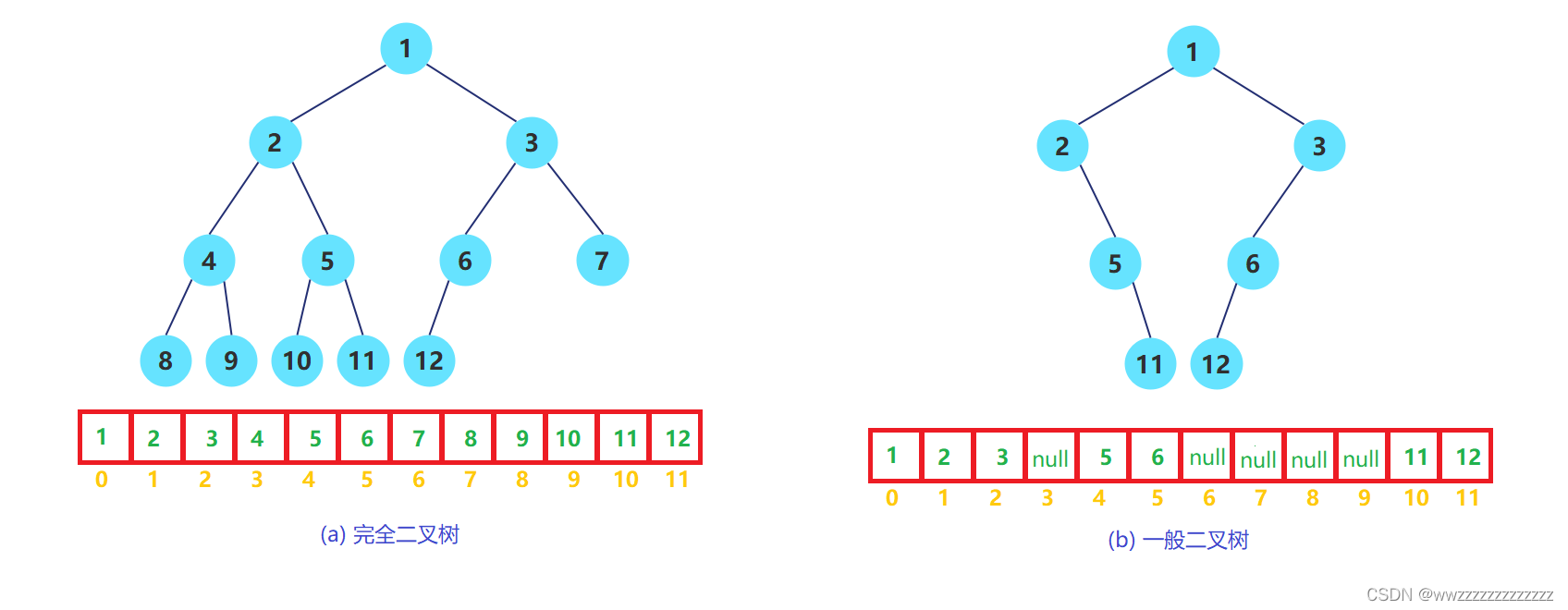

1.2 下标的关系

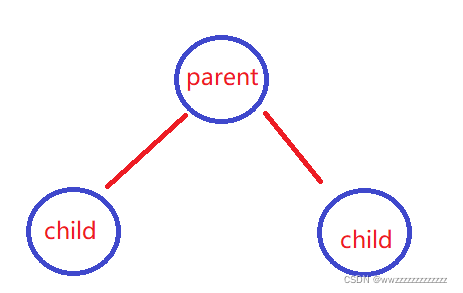
1. **如果 已知双亲下标(parent) ,则:**左孩子的下标(left child) = 2 * parent + 1; 右孩子的下标(right child) = 2 * parent + 2;
2. **如果 已知任意孩子下标(child),则:**双亲的下标(parent) = ( child - 1 ) / 2;

2.堆

2.1 概念

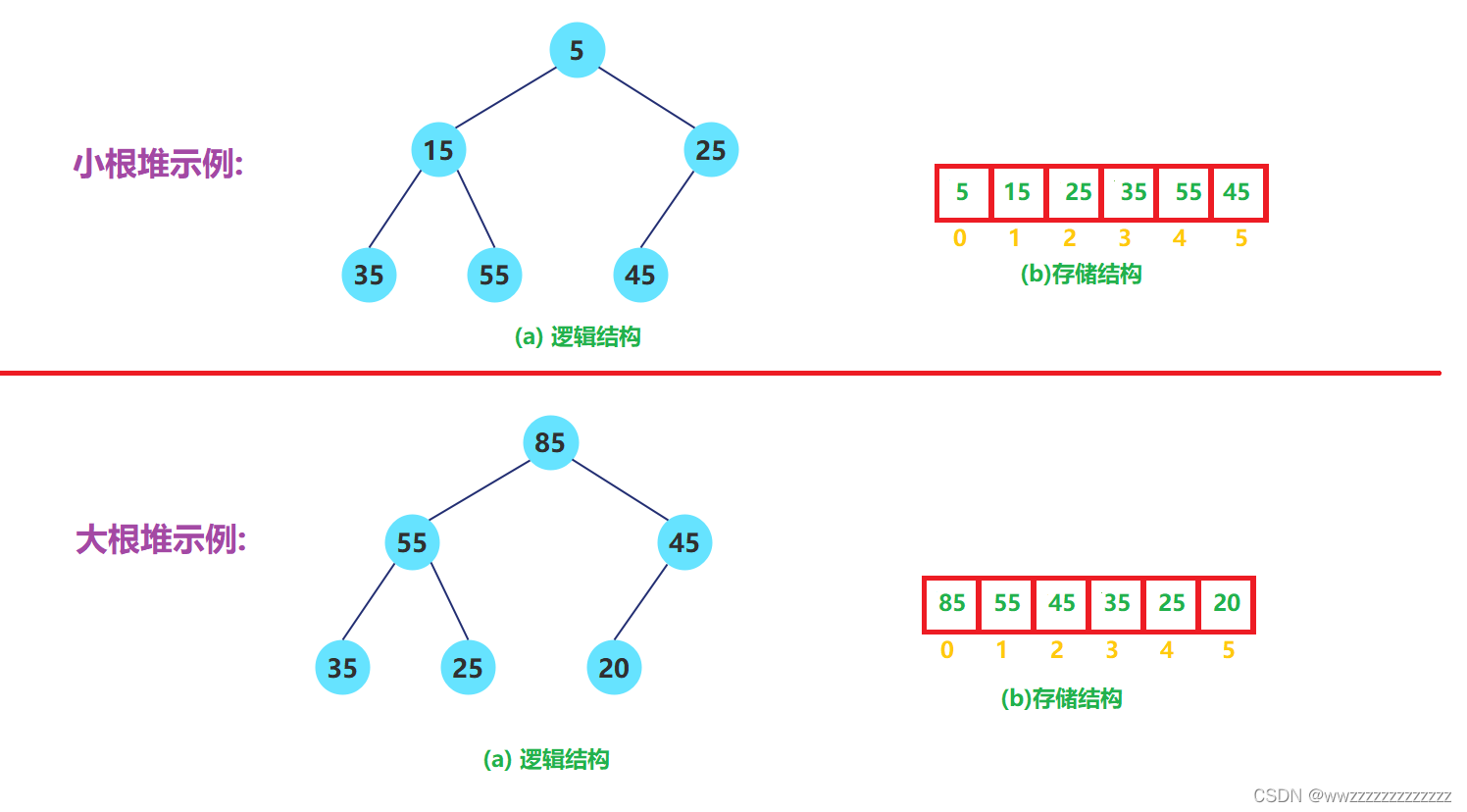
1. 堆逻辑上是一棵完全二叉树
2. 堆物理上是保存在数组中
3. 满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆
4. 反之，则是小堆，或者小根堆，或者最小堆
5. 堆的基本作用是，快速找集合中的最值

3.模拟实现PriorityQueue

①基本操作

classTestHeap{publicint[] elem;publicint usedSize;publicTestHeap(){this.elem =newint[10];}}

②向下调整

思路: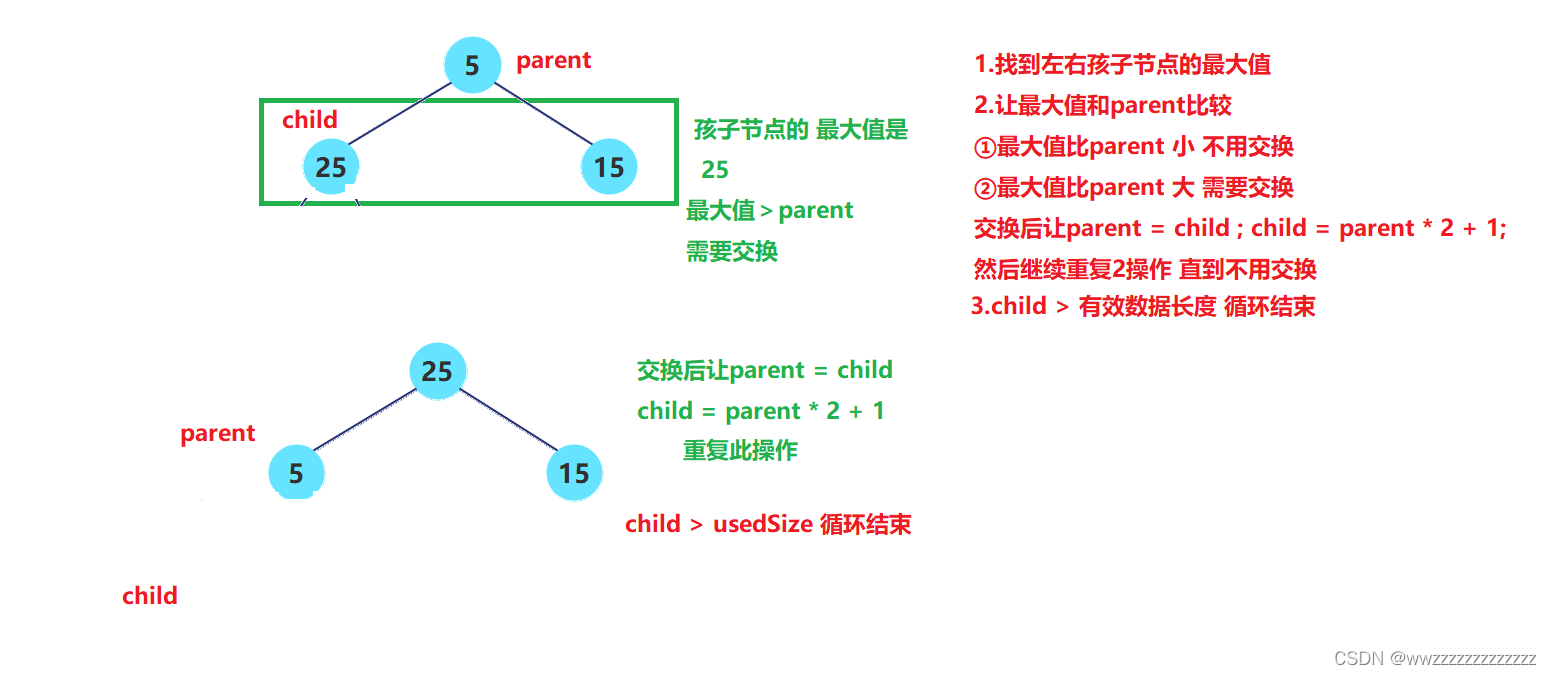

代码实现:

//len是有效数据长度publicvoidadjustDown(int root,int len){int parent = root;int child =2* parent +1;while(child < len){//找到左右孩子的最大值//1. 没有右孩子,左孩子就是最大.child下标下就是最大//2. 有右孩子,但是左孩子更大,即左孩子是最大.child下标下就是最大//3. 有右孩子,但是右孩子更大,即右孩子是最大.child+1 下标下就是最大if(child+1< len &&this.elem[child]<this.elem[child+1]){
                child++;}//此时child下标下就是最大值.if(this.elem[child]>this.elem[parent]){int tmp =this.elem[child];this.elem[child]=this.elem[parent];this.elem[parent]= tmp;
                parent = child;
                child =2* parent +1;}else{break;}}}

③建堆

建大堆 - 思路:
从最后一个数据的 双亲开始 向下调整. 每次调整完 让parent-- 直到调整到parent = 0;

/**
     * 建大堆
     * @param array
     */publicvoidcreateHeap(int[] array){//这一步相当于 数组的拷贝for(int i =0; i < array.length; i++){this.elem[i]= array[i];this.usedSize++;}//parent 就代表每颗子树的根节点for(int parent =(array.length-1-1)/2;parent >=0; parent--){adjustDown(parent,this.usedSize);}}

时间复杂度的分析: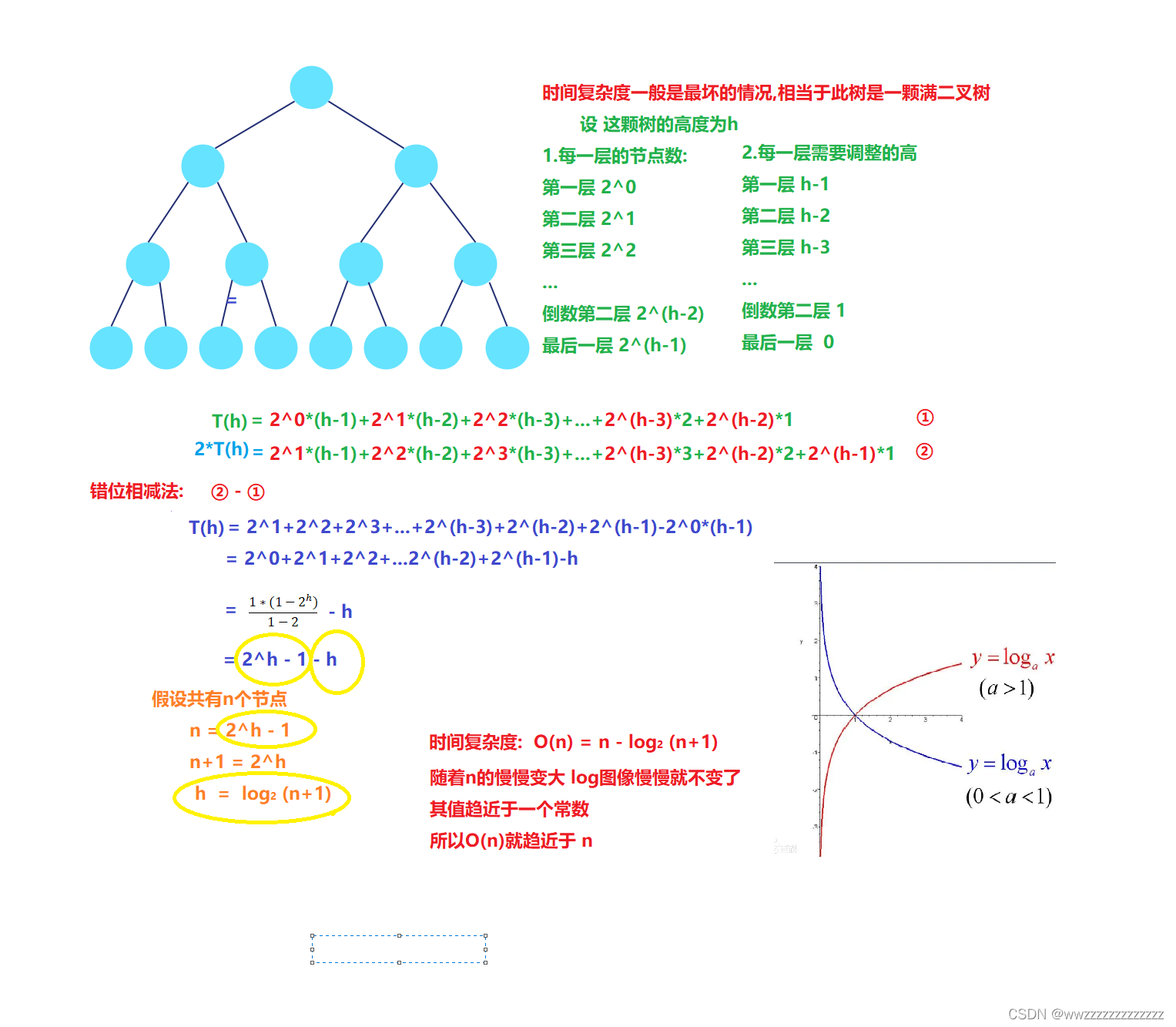

④入队列

思路:从队尾入,每次入队列都要进行向上调整
向上调整:
① 如果插入的child比parent大 则需要交换
② 交换后需要让child = parent; parent = (child - ) / 2;
③ 如果插入的child比parent小 则不需要交换
④循环①②③操作,直到不需要交换或则 child<0结束循环.

代码实现:

publicvoidadjustUp(int child){//parent等于child的双亲int parent =(child -1)/2;//child>0进入循环while(child >0){if(this.elem[child]>this.elem[parent]){int tmp =this.elem[parent];this.elem[parent]=this.elem[child];this.elem[child]= tmp;
                child = parent;
                parent =(child -1)/2;}else{//不需要交换直接跳出循环break;}}}

入队思路:
1.首先判断是否需要扩容
2.如果需要扩容则要先扩容然后插入,不需要扩容直接插入
3.插入后进行向上调整
代码实现:

publicvoidpush(int val){if(isFull()){//扩容Arrays.copyOf(this.elem,2*this.elem.length);}//插入   向上调整this.elem[this.usedSize++]= val;adjustUp(usedSize -1);}//判断是否满publicbooleanisFull(){returnthis.usedSize ==this.elem.length;}

⑤出队列

出队列思路:
1.首先需要判断是否为空
2.为空直接返回
3.不为空,首先交换队首元素和队尾元素,然后从0下标开始进行向下调整.

代码实现:

//判断是否为空publicbooleanisEmpty(){returnthis.usedSize ==0;}publicvoidpop(){if(!isEmpty()){//不为空首先进行交换int tmp =this.elem[0];this.elem[0]=this.elem[usedSize -1];this.elem[usedSize -1]= tmp;this.usedSize--;//然后进行向下调整adjustDown(0,this.usedSize);}}

⑥堆排序

堆排序思路:
1.让end指向队尾元素
2.让队首元素和end交换
3.从0下标位置进行向下调整 然后end–;
4.重复以上操作直到end=0;

代码实现:

/**
     * 前提是要先创建大堆
     */publicvoidheapSort(){int end =this.usedSize -1;while(end >0){int tmp =this.elem[0];this.elem[0]=this.elem[end];this.elem[end]= tmp;adjustDown(0,end--);}}

4.堆的应用-优先级队列

4.1 java 中的优先级队列

PriorityQueue implements Queue

错误处理抛出异常返回特殊值入队列add(e)offer(e)出队列remove()poll()队首元素element()peek()

4.2 java 中堆的使用

注意:

1. 堆的默认大小是 11 默认为小堆
2. 可以指定堆的大小,可以指定堆为大小堆.

publicstaticvoid main (String[] args){//堆 默认是大小为11PriorityQueue<Integer> priorityQueue =newPriorityQueue<>();//默认是 小堆
        priorityQueue.add(1);
        priorityQueue.add(2);
        priorityQueue.add(3);System.out.println(priorityQueue);}

5. 集合框架中PriorityQueue的比较方式

集合框架中的PriorityQueue底层使用堆结构，因此其内部的元素必须要能够比大小，PriorityQueue采用了：
Comparble和Comparator两种方式。

1. Comparble是默认的内部比较方式，如果用户插入自定义类型对象时，该类对象必须要实现Comparble接 口，并覆写compareTo方法
2. 用户也可以选择使用比较器对象，如果用户插入自定义类型对象时，必须要提供一个比较器类，让该类实现 Comparator接口并覆写compare方法。

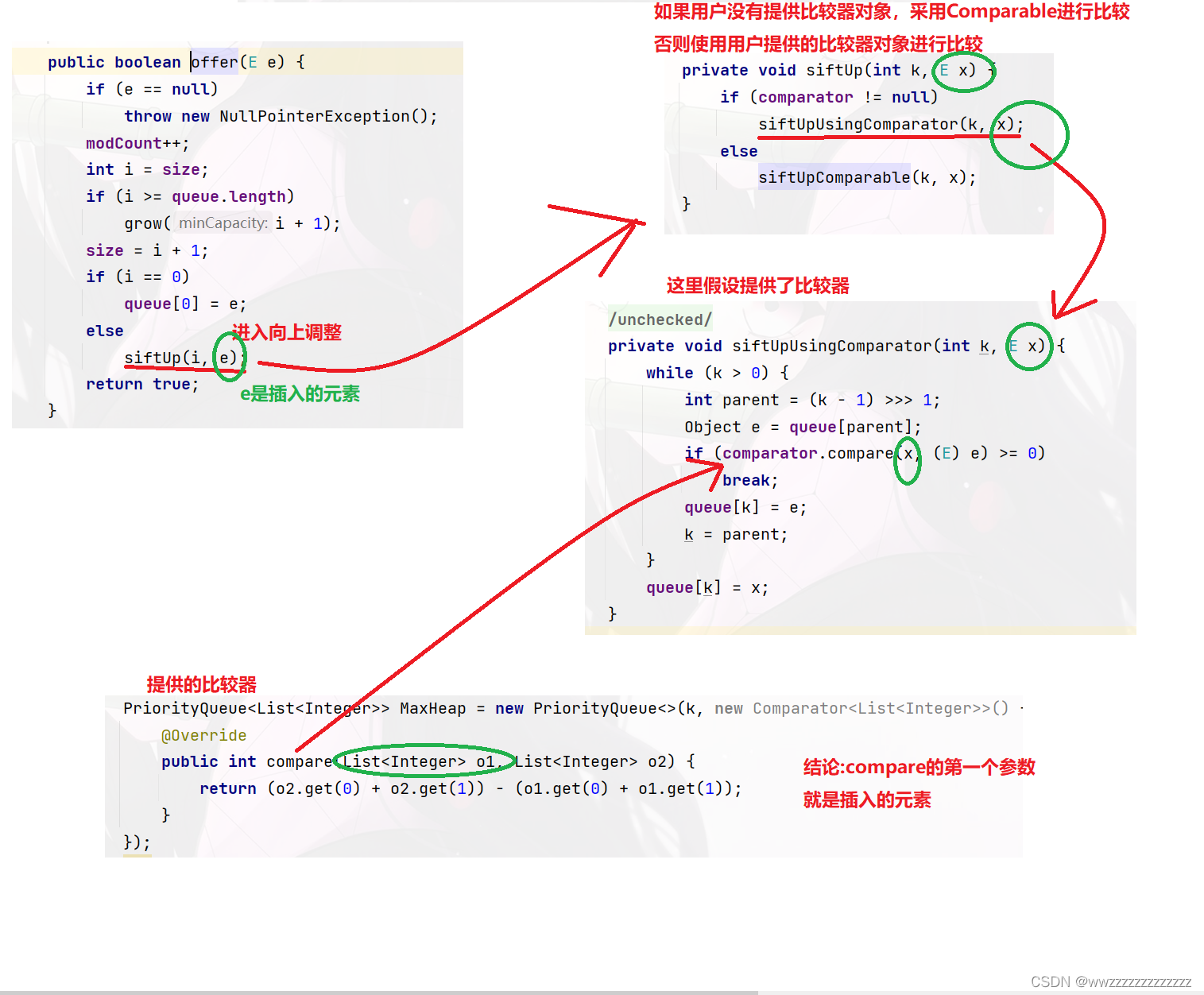
6.堆的其他应用-TopK 问题

TopK问题,找前K个最大(最小)的数.

用堆的思路:

1. 放入k个元素到堆中 ①找前k个最大的数,建小堆. ②找前k个最小的数,建大堆.
2. 如果找的是前k个最大的数,先建小堆将k个元素放入堆中,然后让堆顶元素 和 后面的数比较,如果小于后面的数,就和堆顶元素交换,然后变成小堆继续此操作.
3. 反之则是找前k个最小的数.
4. 遍历结束后,堆中的元素就是要找的数

画图解析:

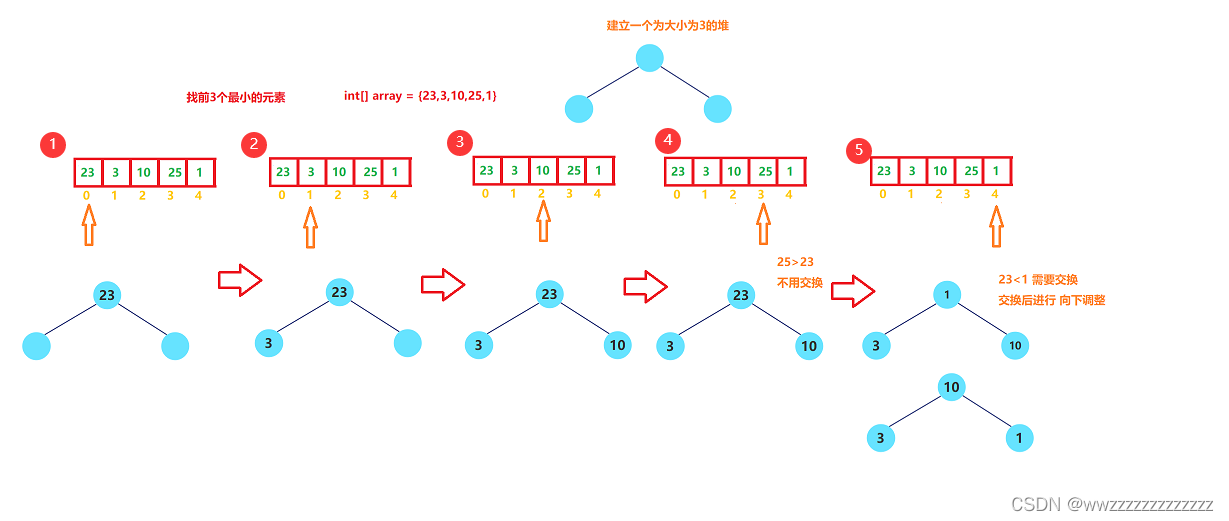
代码实现:

/**
     * 找前k个最大的元素
     * @param array
     * @param k
     */publicstaticvoidtopk2(int[] array,int k){PriorityQueue<Integer> maxHeap =newPriorityQueue<>(k,newComparator<Integer>(){@Overridepublicintcompare(Integer o1,Integer o2){return o1 - o2;//大堆}});for(int i =0; i < array.length; i++){if(maxHeap.size()< k){
                maxHeap.offer(array[i]);}else{int top = maxHeap.peek();//获取队顶元素if(top < array[i]){
                    maxHeap.poll();
                    maxHeap.offer(array[i]);}}}System.out.println(maxHeap);}/**
     * 找前k个最小的元素
     * @param array
     * @param k
     */publicstaticvoidtopk1(int[] array,int k){PriorityQueue<Integer> maxHeap =newPriorityQueue<>(k,newComparator<Integer>(){@Overridepublicintcompare(Integer o1,Integer o2){return o2 - o1;//大堆}});for(int i =0; i < array.length; i++){if(maxHeap.size()< k){
                maxHeap.offer(array[i]);}else{int top = maxHeap.peek();//获取队顶元素if(top > array[i]){
                    maxHeap.poll();
                    maxHeap.offer(array[i]);}}}System.out.println(maxHeap);}publicstaticvoidmain(String[] args){int[] array ={1,3,2,6,5,78,22,15,28};//找前3个最大的数据.topk1(array,3);topk2(array,4);}

运行结果:

7.面试题—查找和最小的K对数字

LeetCode 373: 查找和最小的K对数字
描述:
给定两个以升序排列的整数数组 nums1 和 nums2 , 以及一个整数 k 。
定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。
请找到和最小的 k 个数对 (u1,v1), (u2,v2) … (uk,vk) 。
示例 1:

输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
输出: [1,2],[1,4],[1,6]
解释: 返回序列中的前 3 对数：
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

解题思路:

1. 根据题意找最小的k对数字,建立大小为k的大堆
2. 如果堆没放满,直接放入堆中.
3. 如果堆放满了,每次需要和堆顶比较,如果小于堆顶,需要交换.
4. 遍历时注意,如果数组过大,遍历会超时,所以遍历次数可以优化为 只最多遍历到 k，而且要满足小于数组长度的要求.(i<k && i<nums.length)
5. 在遍历结束后,将数据插入list中的时候注意.可能堆没满.

代码实现:

classSolution{publicList<List<Integer>>kSmallestPairs(int[] nums1,int[] nums2,int k){PriorityQueue<List<Integer>>MaxHeap=newPriorityQueue<>(k,newComparator<List<Integer>>(){@Overridepublicintcompare(List<Integer> o1,List<Integer> o2){return(o2.get(0)+ o2.get(1))-(o1.get(0)+ o1.get(1));}});// 只最多遍历到 k，而且要满足小于数组长度的要求for(int i =0; i < nums1.length && i < k; i++){for(int j =0; j < nums2.length && j < k; j++){// 堆没满 首先放入堆中if(MaxHeap.size()< k){List<Integer> list1 =newArrayList<>();
                    list1.add(nums1[i]);
                    list1.add(nums2[j]);MaxHeap.offer(list1);}else{List<Integer> top =MaxHeap.peek();int topValue = top.get(0)+ top.get(1);//堆满了后要进行比较,大于堆顶的值要出队然后把大于的数据入队if(topValue > nums1[i]+ nums2[j]){MaxHeap.poll();List<Integer> list1 =newArrayList<>();
                        list1.add(nums1[i]);
                        list1.add(nums2[j]);MaxHeap.offer(list1);}}}}//将数据放入ret中要注意 可能堆没放满List<List<Integer>> ret =newArrayList<>();for(int i =0; i < k &&!MaxHeap.isEmpty(); i++){
            ret.add(MaxHeap.poll());}return ret;}}