高斯混合模型(gmm)是将数据表示为高斯(正态)分布的混合的统计模型。这些模型可用于识别数据集中的组,并捕获数据分布的复杂、多模态结构。
gmm可用于各种机器学习应用,包括聚类、密度估计和模式识别。
在本文中,将首先探讨混合模型,重点是高斯混合模型及其基本原理。然后将研究如何使用一种称为期望最大化(EM)的强大技术来估计这些模型的参数,并提供在Python中从头开始实现它。最后将演示如何使用Scikit-Learn库使用GMM执行聚类。
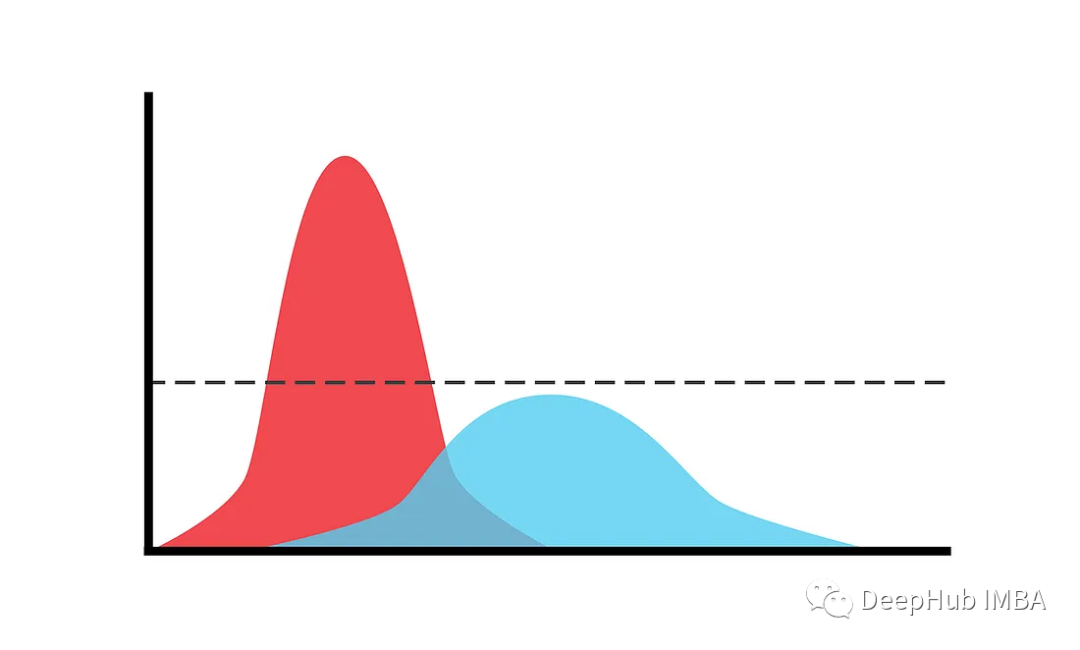
混合模型
混合模型是一种概率模型,用于表示可能来自多个不同来源或类别的数据,每个来源或类别都由单独的概率分布建模。例如,金融回报在正常市场条件下和危机期间的表现通常不同,因此可以将其建模为两种不同分布的混合。
形式上,如果X是随机变量,其分布是K个分量分布的混合,则X的概率密度函数(PDF)或概率质量函数(PMF)可表示为:
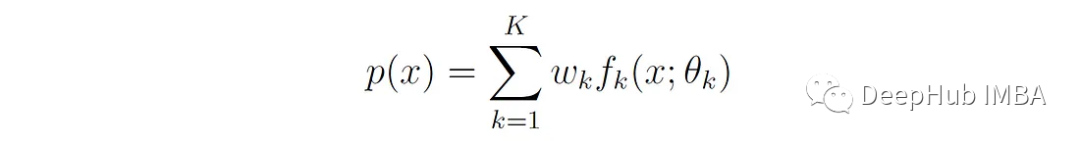
P (x)是混合模型的总密度或质量函数。K是混合模型中组分分布的数目。
fₖ(x;θₖ)是第k个分量分布的密度或质量函数,参数化为θₖ。
Wₖ为第k个分量的混合权值,0≤Wₖ≤1,权值之和为1。Wₖ也称为分量k的先验概率。
θₖ表示第k个分量的参数,例如高斯分布中的平均值和标准差。
混合模型假设每个数据点来自K个分量分布中的一个,根据混合权重wₖ选择具体的分布。该模型不需要知道每个数据点属于哪个分布。
高斯混合模型(Gaussian mixture model, GMM)是一种常见的混合模型,其概率密度由高斯分布的混合给出:
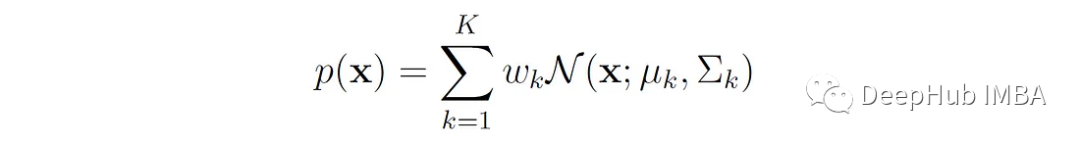
X是一个d维向量。
μₖ是第k个高斯分量的平均向量。
Σₖ是第k个高斯分量的协方差矩阵。
N (x;μₖ,Σₖ)为第k个分量的多元正态密度函数:
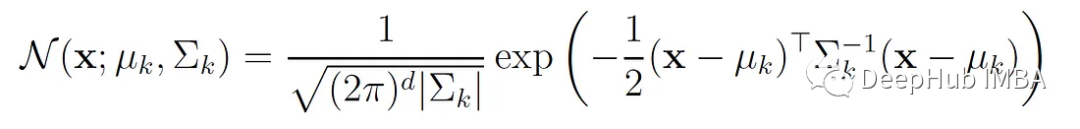
对于单变量高斯分布,概率密度可以简化为:
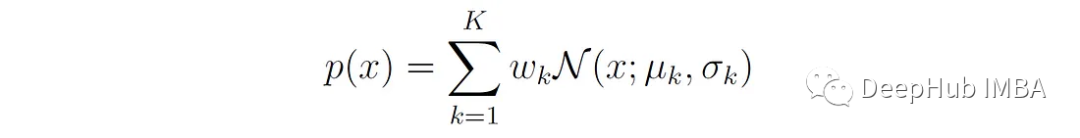
μₖ是第k个高斯分量的平均值。
σₖ是第k个高斯分量的协方差矩阵。
N (x;μₖ,σₖ)为第k个分量的单变量正态密度函数:
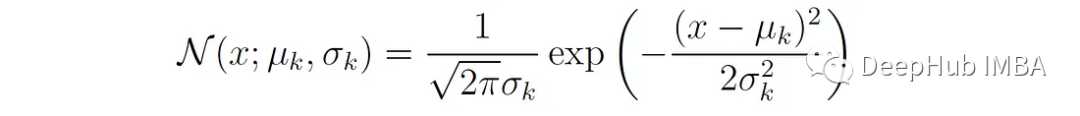
下面的Python函数绘制了两个单变量高斯分布的混合分布:
from scipy.stats import norm
def plot_mixture(mean1, std1, mean2, std2, w1, w2):
# Generate points for the x-axis
x = np.linspace(-5, 10, 1000)
# Calculate the individual nomral distributions
normal1 = norm.pdf(x, mean1, std1)
normal2 = norm.pdf(x, mean2, std2)
# Calculate the mixture
mixture = w1 * normal1 + w2 * normal2
# Plot the results
plt.plot(x, normal1, label='Normal distribution 1', linestyle='--')
plt.plot(x, normal2, label='Normal distribution 2', linestyle='--')
plt.plot(x, mixture, label='Mixture model', color='black')
plt.xlabel('$x$')
plt.ylabel('$p(x)$')
plt.legend()
我们用这个函数来绘制两个高斯分布的混合物,如果参数为μ₁= -1,σ₁= 1,μ₂= 4,σ₂= 1.5,混合权为w₁= 0.7和w₂= 0.3:
# Parameters for the two univariate normal distributions
mean1, std1 = -1, 1
mean2, std2 = 4, 1.5
w1, w2 = 0.7, 0.3
plot_mixture(mean1, std1, mean2, std2, w1, w2)
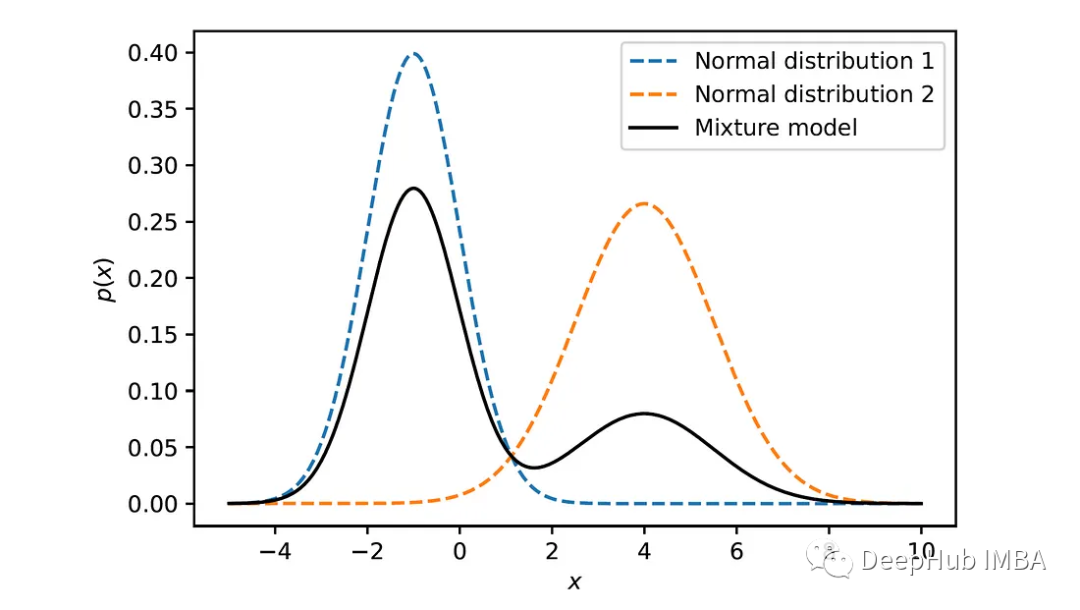
虚线表示单个正态分布,黑色实线表示结果的混合。该图说明了混合模型如何将两个分布组合在一起,每个分布都有自己的平均值、标准差和总体混合结果中的权重。
学习GMM参数
我们学习的目标是找到最能解释观测数据的GMM参数(均值、协方差和混合系数)。为此,需要首先定义给定输入数据的模型的可能性。
对于具有K个分量的GMM,数据集X = {X 1,…,X 1} (n个数据点),似然函数L由每个数据点的概率密度乘积给出,由GMM定义:
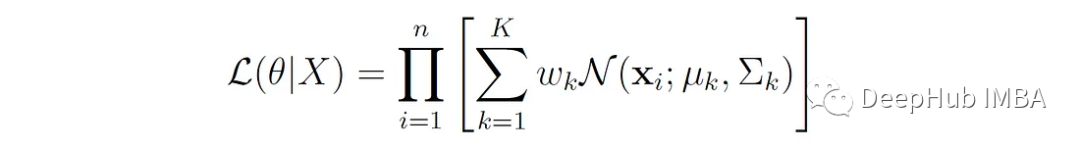
其中,θ表示模型的所有参数(均值、方差和混合权重)。
在实际应用中,使用对数似然更容易,因为概率的乘积可能导致大型数据集的数值下溢。对数似然由下式给出:
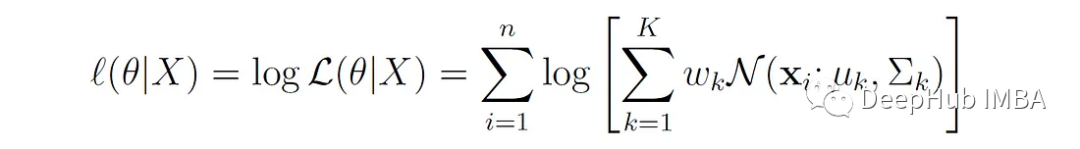
GMM的参数可以通过对θ最大化对数似然函数来估计。但是我们不能直接应用极大似然估计(MLE)来估计GMM的参数:
对数似然函数是高度非线性的,难于解析最大化。
该模型具有潜在变量(混合权重),这些变量在数据中不能直接观察到。
为了克服这些问题,通常使用期望最大化(EM)算法来解决这个问题
期望最大化(EM)
EM算法是在依赖于未观察到的潜在变量的统计模型中寻找参数的最大似然估计的有力方法。
该算法首先随机初始化模型参数。然后在两个步骤之间迭代:
1、期望步(e步):根据观察到的数据和模型参数的当前估计,计算模型相对于潜在变量分布的期望对数似然。这一步包括对潜在变量的概率进行估计。
2、最大化步骤(m步):更新模型的参数,以最大化观察数据的对数似然,给定e步骤估计的潜在变量。
这两个步骤重复直到收敛,通常由对数似然变化的阈值或迭代的最大次数决定。
在GMMs中,潜在变量表示每个数据点的未知分量隶属度。设Z′为随机变量,表示生成数据点x′的分量。Z′可以取值{1,…,K}中的一个,对应于K个分量。
E-Step
在e步中,我们根据模型参数的当前估计值计算潜在变量Z ^的概率分布。换句话说,我们计算每个高斯分量中每个数据点的隶属度概率。
Z′= k的概率,即x′属于第k个分量,可以用贝叶斯规则计算:
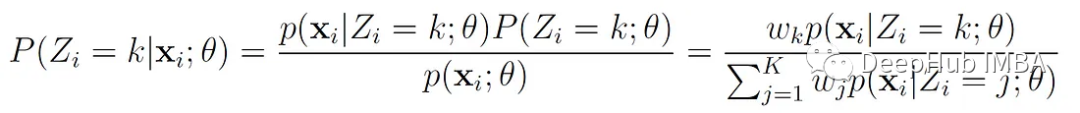
我们用变量γ(z′ₖ)来表示这个概率,可以这样写:
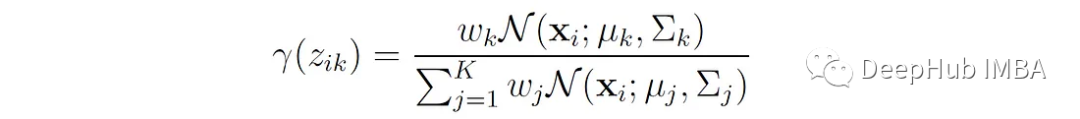
变量γ(z′ₖ)通常被称为responsibilities,因为它们描述了每个分量对每个观测值的responsibilities。这些参数作为关于潜在变量的缺失信息的代理。
关于潜在变量分布的期望对数似然现在可以写成:
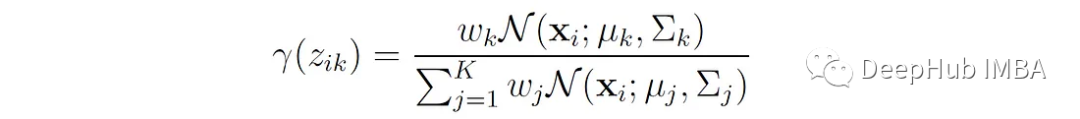
函数Q是每个高斯分量下所有数据点的对数似然的加权和,权重就是我们上面说的responsibilities。Q不同于前面显示的对数似然函数l(θ|X)。对数似然l(θ|X)表示整个混合模型下观测数据的似然,没有明确考虑潜在变量,而Q表示观测数据和估计潜在变量分布的期望对数似然。
M-Step
在m步中,更新GMM的参数θ(均值、协方差和混合权值),以便使用e步中计算的最大化期望似然Q(θ)。
参数更新如下:
1、更新每个分量的方法:
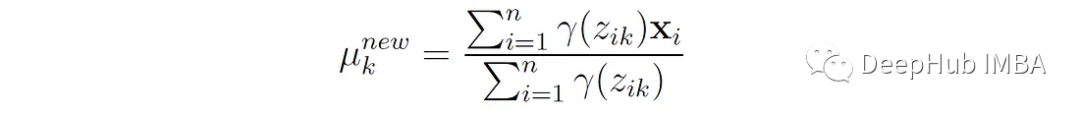
第k个分量的新平均值是所有数据点的加权平均值,权重是这些点属于分量k的概率。这个更新公式可以通过最大化期望对数似然函数Q相对于平均值μₖ而得到。
以下是证明步骤,单变量高斯分布的期望对数似然为:
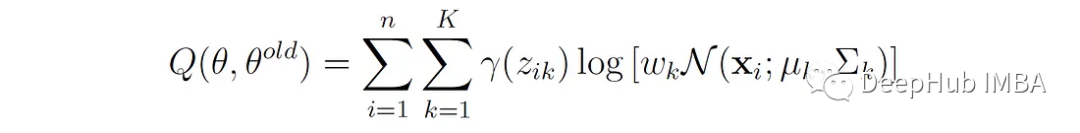
这个函数对μₖ求导并设其为0,得到:
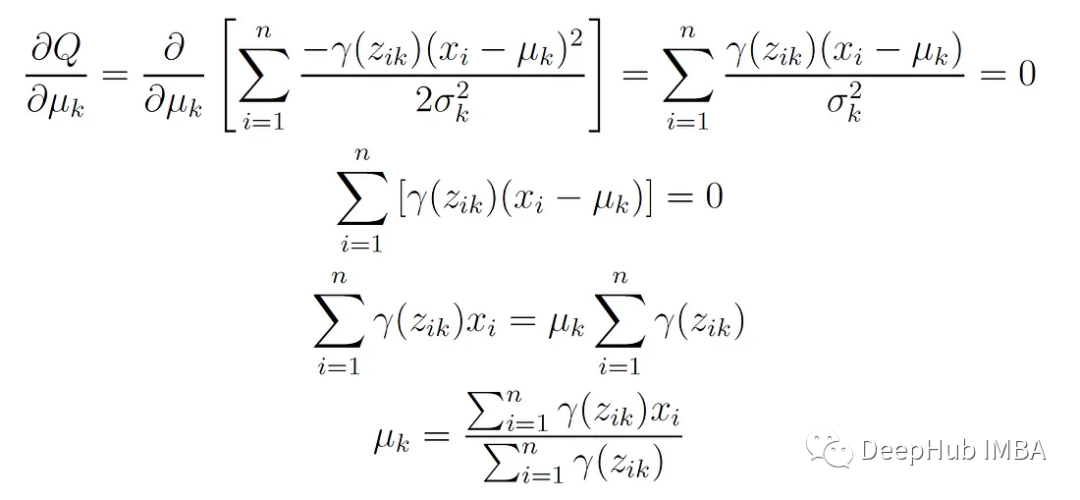
2、更新每个分量的协方差:
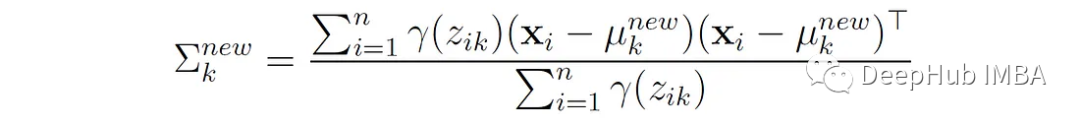
也就是说,第k个分量的新协方差是每个数据点与该分量均值的平方偏差的加权平均值,其中权重是分配给该分量的点的概率。
在单变量正态分布的情况下,此更新简化为:
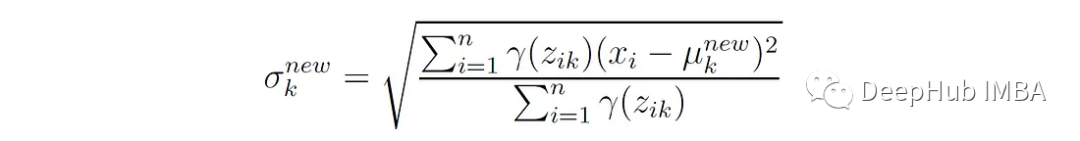
3、更新混合权值
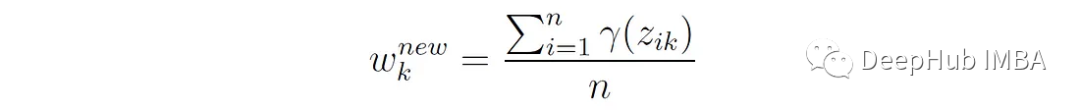
也就是说,第k个分量的新权重是属于该分量的点的总概率,用n个点的个数归一化。
重复这两步保证收敛到似然函数的局部最大值。由于最终达到的最优取决于初始随机参数值,因此通常的做法是使用不同的随机初始化多次运行EM算法,并保留获得最高似然的模型。
Python实现
下面将使用Python实现EM算法,用于从给定数据集估计两个单变量高斯分布的GMM的参数。
首先导入所需的库:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
np.random.seed(0) # for reproducibility
接下来,让我们编写一个函数来初始化GMM的参数:
def init_params(x):
"""Initialize the parameters for the GMM
"""
# Randomly initialize the means to points from the dataset
mean1, mean2 = np.random.choice(x, 2, replace=False)
# Initialize the standard deviations to 1
std1, std2 = 1, 1
# Initialize the mixing weights uniformly
w1, w2 = 0.5, 0.5
return mean1, mean2, std1, std2, w1, w2
均值从数据集中的随机数据点初始化,标准差设为1,混合权重设为0.5。
e步,计算属于每个高斯分量的每个数据点的概率:
def e_step(x, mean1, std1, mean2, std2, w1, w2):
"""E-Step: Compute the responsibilities
"""
# Compute the densities of the points under the two normal distributions
prob1 = norm(mean1, std1).pdf(x) * w1
prob2 = norm(mean2, std2).pdf(x) * w2
# Normalize the probabilities
prob_sum = prob1 + prob2
prob1 /= prob_sum
prob2 /= prob_sum
return prob1, prob2
m步,根据e步计算来更新模型参数:
def m_step(x, prob1, prob2):
"""M-Step: Update the GMM parameters
"""
# Update means
mean1 = np.dot(prob1, x) / np.sum(prob1)
mean2 = np.dot(prob2, x) / np.sum(prob2)
# Update standard deviations
std1 = np.sqrt(np.dot(prob1, (x - mean1)**2) / np.sum(prob1))
std2 = np.sqrt(np.dot(prob2, (x - mean2)**2) / np.sum(prob2))
# Update mixing weights
w1 = np.sum(prob1) / len(x)
w2 = 1 - w1
return mean1, std1, mean2, std2, w1, w2
最后编写运行EM算法的主函数,在e步和m步之间迭代指定次数的迭代:
def gmm_em(x, max_iter=100):
"""Gaussian mixture model estimation using Expectation-Maximization
"""
mean1, mean2, std1, std2, w1, w2 = init_params(x)
for i in range(max_iter):
print(f'Iteration {i}: μ1 = {mean1:.3f}, σ1 = {std1:.3f}, μ2 = {mean2:.3f}, σ2 = {std2:.3f}, '
f'w1 = {w1:.3f}, w2 = {w2:.3f}')
prob1, prob2 = e_step(x, mean1, std1, mean2, std2, w1, w2)
mean1, std1, mean2, std2, w1, w2 = m_step(x, prob1, prob2)
return mean1, std1, mean2, std2, w1, w2
为了测试我们的实现,需要将通过从具有预定义参数的已知混合分布中采样数据来创建一个合成数据集。然后将使用EM算法估计分布的参数,并将估计的参数与原始参数进行比较。
首先从两个单变量正态分布的混合物中采样数据:
def sample_data(mean1, std1, mean2, std2, w1, w2, n_samples):
"""Sample random data from a mixture of two Gaussian distribution.
"""
x = np.zeros(n_samples)
for i in range(n_samples):
# Choose distribution based on mixing weights
if np.random.rand() < w1:
# Sample from the first distribution
x[i] = np.random.normal(mean1, std1)
else:
# Sample from the second distribution
x[i] = np.random.normal(mean2, std2)
return x
然后使用这个函数从之前定义的混合分布中采样1000个数据点:
# Parameters for the two univariate normal distributions
mean1, std1 = -1, 1
mean2, std2 = 4, 1.5
w1, w2 = 0.7, 0.3
x = sample_data(mean1, std1, mean2, std2, w1, w2, n_samples=1000)
现在可以在这个数据集上运行EM算法:
final_dist_params = gmm_em(x, max_iter=30)
得到以下输出:
Iteration 0: μ1 = -1.311, σ1 = 1.000, μ2 = 0.239, σ2 = 1.000, w1 = 0.500, w2 = 0.500
Iteration 1: μ1 = -1.442, σ1 = 0.898, μ2 = 2.232, σ2 = 2.521, w1 = 0.427, w2 = 0.573
Iteration 2: μ1 = -1.306, σ1 = 0.837, μ2 = 2.410, σ2 = 2.577, w1 = 0.470, w2 = 0.530
Iteration 3: μ1 = -1.254, σ1 = 0.835, μ2 = 2.572, σ2 = 2.559, w1 = 0.499, w2 = 0.501
...
Iteration 27: μ1 = -1.031, σ1 = 1.033, μ2 = 4.180, σ2 = 1.371, w1 = 0.675, w2 = 0.325
Iteration 28: μ1 = -1.031, σ1 = 1.033, μ2 = 4.181, σ2 = 1.370, w1 = 0.675, w2 = 0.325
Iteration 29: μ1 = -1.031, σ1 = 1.033, μ2 = 4.181, σ2 = 1.370, w1 = 0.675, w2 = 0.325
该算法收敛到接近原始参数的参数:μ₁= -1.031,σ₁= 1.033,μ₂= 4.181,σ₂= 1.370,混合权值w₁= 0.675,w₂= 0.325。
让我们使用前面编写的plot_mixture()函数来绘制最终分布,绘制采样数据的直方图:
def plot_mixture(x, mean1, std1, mean2, std2, w1, w2):
# Plot an histogram of the input data
sns.histplot(x, bins=20, kde=True, stat='density', linewidth=0.5, color='gray')
# Generate points for the x-axis
x_ = np.linspace(-5, 10, 1000)
# Calculate the individual nomral distributions
normal1 = norm.pdf(x_, mean1, std1)
normal2 = norm.pdf(x_, mean2, std2)
# Calculate the mixture
mixture = w1 * normal1 + w2 * normal2
# Plot the results
plt.plot(x_, normal1, label='Normal distribution 1', linestyle='--')
plt.plot(x_, normal2, label='Normal distribution 2', linestyle='--')
plt.plot(x_, mixture, label='Mixture model', color='black')
plt.xlabel('$x$')
plt.ylabel('$p(x)$')
plt.legend()
plot_mixture(x, *final_dist_params)
结果如下图所示:
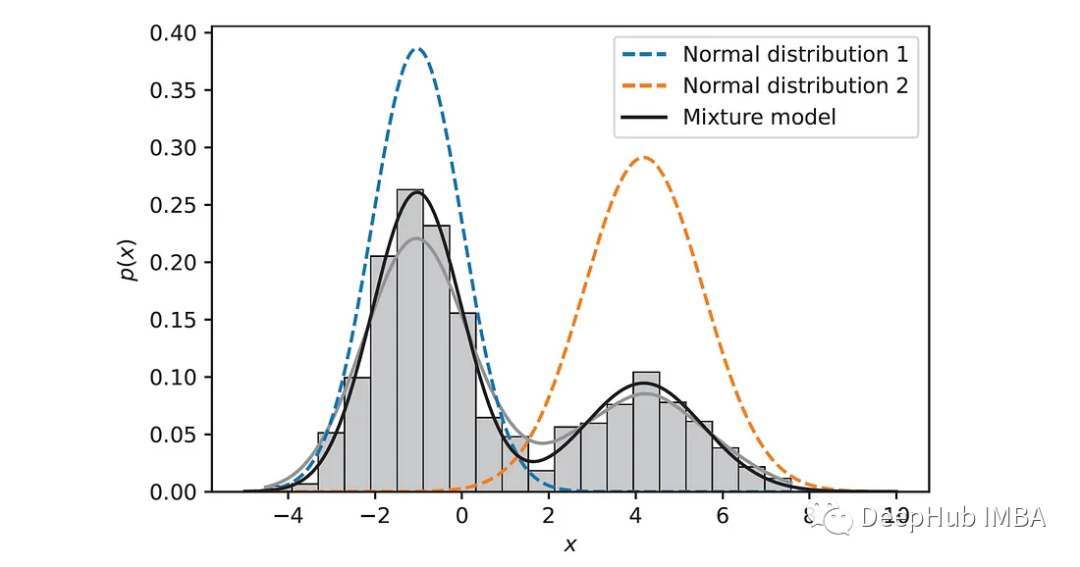
可以看出,估计的分布与数据点的直方图密切一致。以上是为了我们了解算法进行的Python代码,但是在实际使用的时候还会存在很多问题,所以如果要实际中应用,可以直接使用Sklearn的实现。
Scikit-Learn中的GMM
Scikit-Learn在类sklearn.mixture.GaussianMixture中提供了高斯混合模型的实现。
与Scikit-Learn中的其他聚类算法不同,这个算法不提供labels_属性。因此要获得数据点的聚类分配,需要调用拟合模型上的predict()方法(或调用fit_predict())。
下面使用这个类对以下数据集执行聚类,该数据集由两个椭圆blobs和一个球形blobs组成:
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=500, centers=[(0, 0), (4, 4)], random_state=0)
# Apply a linear transformation to make the blobs elliptical
transformation = [[0.6, -0.6], [-0.2, 0.8]]
X = np.dot(X, transformation)
# Add another spherical blob
X2, y2 = make_blobs(n_samples=150, centers=[(-2, -2)], cluster_std=0.5, random_state=0)
X = np.vstack((X, X2))
看看我们的数据
def plot_data(X):
sns.scatterplot(x=X[:, 0], y=X[:, 1], edgecolor='k', legend=False)
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plot_data(X)
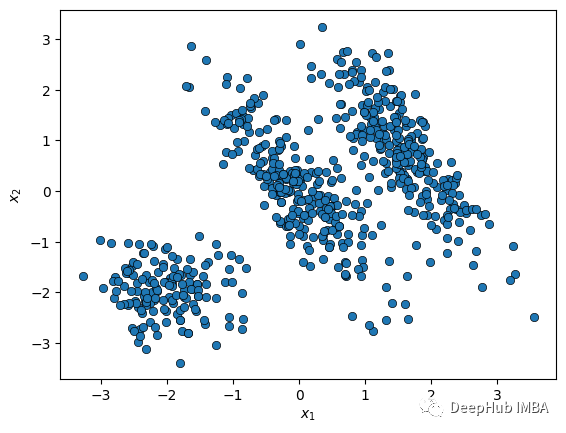
接下来,我们用n_components=3实例化GMMclass,并调用它的fit_predict()方法来获取簇分配:
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3)
labels = gmm.fit_predict(X)
可以检查EM算法收敛需要多少次迭代:
print(gmm.n_iter_)
2
EM算法只需两次迭代即可收敛。检查估计的GMM参数:
print('Weights:', gmm.weights_)
print('Means:\n', gmm.means_)
print('Covariances:\n', gmm.covariances_)
结果如下:
Weights: [0.23077331 0.38468283 0.38454386]
Means:
[[-2.01578902 -1.95662033]
[-0.03230299 0.03527593]
[ 1.56421574 0.80307925]]
Covariances:
[[[ 0.254315 -0.01588303]
[-0.01588303 0.24474151]]
[[ 0.41202765 -0.53078979]
[-0.53078979 0.99966631]]
[[ 0.35577946 -0.48222654]
[-0.48222654 0.98318187]]]
可以看到,估计的权重非常接近三个blob的原始比例,球形blob的均值和方差非常接近其原始参数。
让我们来绘制聚类的结果:
def plot_clusters(X, labels):
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=labels, palette='tab10', edgecolor='k', legend=False)
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plot_clusters(X, labels)
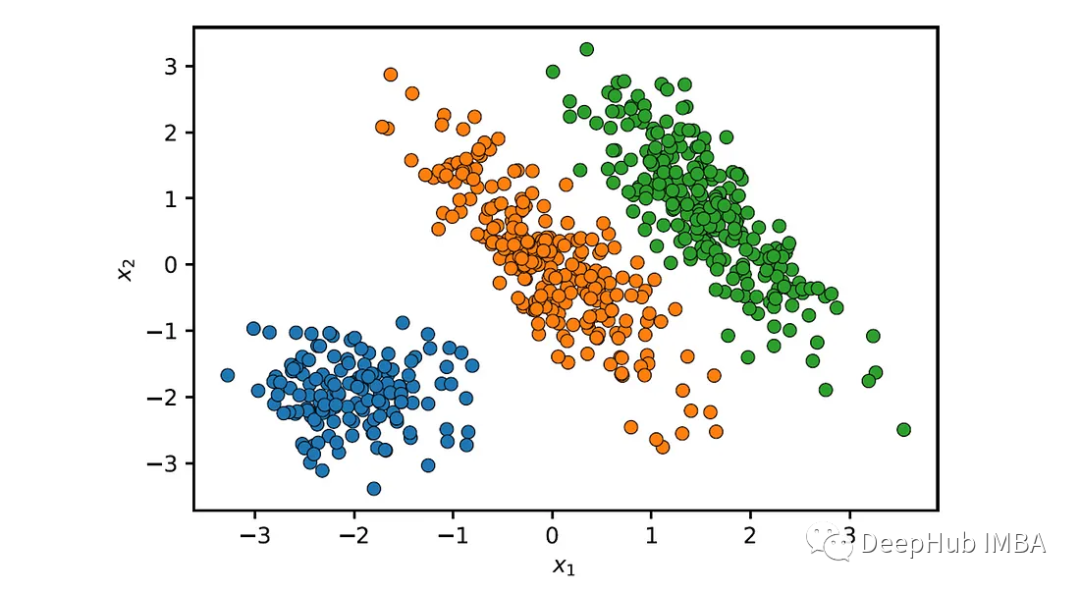
GMM正确地识别了这三个簇。
我们还可以使用predict_proba()方法来获得每个集群中每个数据点的隶属性概率。
prob = gmm.predict_proba(X)
例如,数据集中的第一个点属于绿色簇的概率非常高:
print('x =', X[0])
print('prob =', prob[0])
#x = [ 2.41692591 -0.07769481]
#prob = [3.11052582e-21 8.85973054e-10 9.99999999e-01]
可以通过使每个点的大小与它属于它被分配到的集群的概率成比例来可视化这些概率:
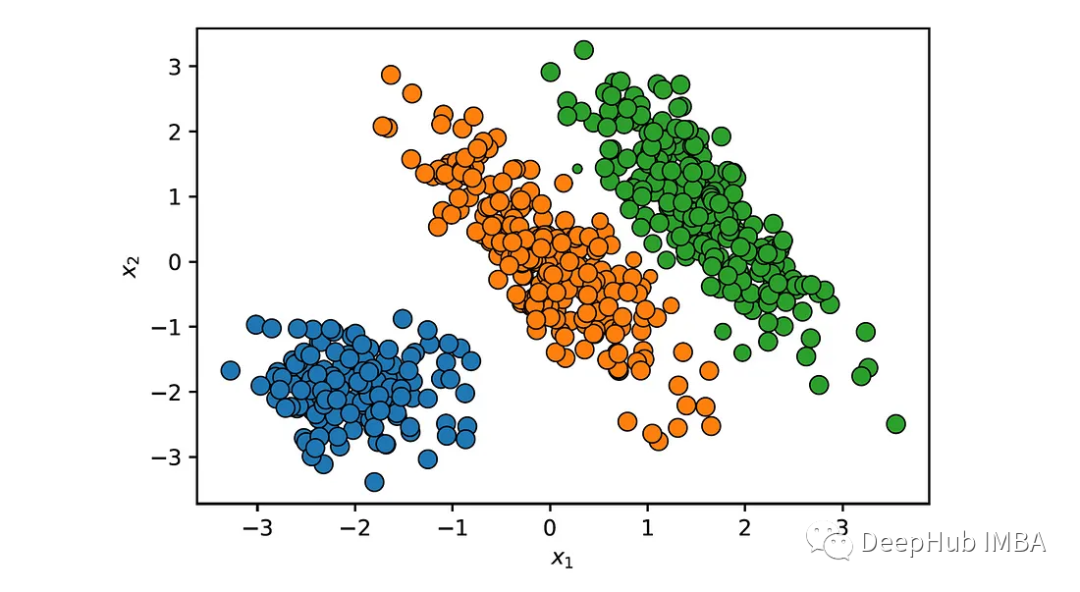
位于两个椭圆簇之间的边界上的点具有较低的概率。具有显著低概率密度(例如,低于预定义阈值)的数据点可以被识别为异常或离群值。
我们还可以与其他的聚类方法作比较
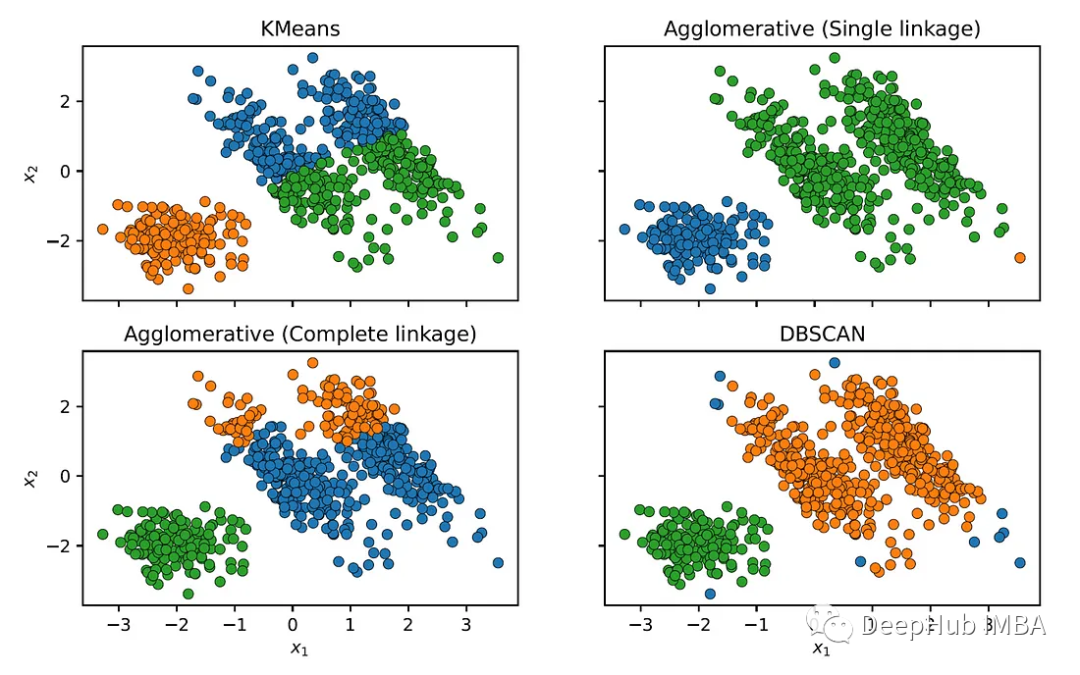
可以看到,其他聚类算法不能正确识别椭圆聚类。
模型评价
对数似然是评估GMMs的主要方法。在训练过程中也可以对其进行监控,检查EM算法的收敛性。为了比较具有不同分量数或不同协方差结构的模型。需要两个额外的度量,它们平衡了模型复杂性(参数数量)和拟合优度(由对数似然表示):
1、Akaike Information Criterion (AIC):
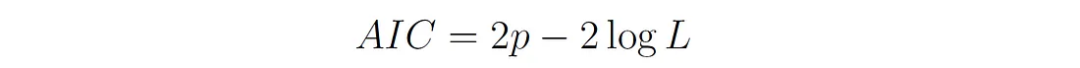
P是模型中参数的个数(包括所有的均值、协方差和混合权值)。L是模型的最大似然(模型具有最优参数值的似然)。
AIC值越低,说明模型越好。AIC奖励与数据拟合良好的模型,但也惩罚具有更多参数的模型。
2、Bayesian Information Criterion (BIC):
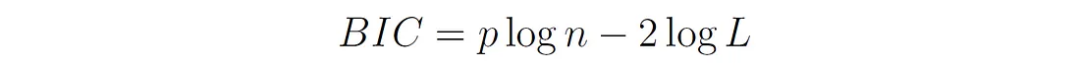
式中p和L的定义与前文相同,n为数据点个数。
与AIC类似,BIC平衡了模型拟合和复杂性,但对具有更多参数的模型施加了更大的惩罚,因为p乘以log(n)而不是2。
在Scikit-Learn中,可以使用gmm类的aic()和bic()方法来计算这些度量。例如上面的GMM聚类的AIC和BIC值为:
print(f'AIC = {gmm.aic(X):.3f}')
print(f'BIC = {gmm.bic(X):.3f}')
#AIC = 4061.318
#BIC = 4110.565
我们可以通过将不同分量数的GMMs拟合到数据集上,然后选择AIC或BIC值最低的模型,从而找到最优的分量数。
总结
最后我们总结一下gmm与其他聚类算法的优缺点:
优点:
与假设球形簇的k-means不同,由于协方差分量,gmm可以适应椭球形状。这使得gmm能够捕获更多种类的簇形状。
由于使用协方差矩阵和混合系数,可以处理不同大小的聚类,这说明了每个聚类的分布和比例。
gmm提供了属于每个簇的每个点的概率(软分配),这可以在理解数据时提供更多信息。
可以处理重叠的集群,因为它根据概率而不是硬边界为集群分配数据点。
易于解释聚类结果,因为每个聚类都由具有特定参数的高斯分布表示。
除了聚类,GMMs还可以用于密度估计和异常检测。
缺点:
需要提前指定分量(簇)的数量。
假设每个集群中的数据遵循高斯分布,这对于实际数据可能并不总是有效的假设。
当集群只包含少量数据点时,可能不能很好地工作,因为模型依赖于足够的数据来准确估计每个分量的参数。
聚类结果对初始参数的选择很敏感。
在GMMs中使用的EM算法会陷入局部最优,收敛速度较慢。
条件差的协方差矩阵(即接近奇异或条件数非常高的矩阵)会导致EM计算过程中的数值不稳定。
与k-means等简单算法相比,计算量更大,特别是对于大型数据集或分量数量很高的情况下。
作者:Roi Yehoshua