目录
一、相关基础
1 相关概念
- 无线传感器网络（Wireless Sensor Networks，WSNs）是一种分布式传感网络，嵌入了传感器的智能设备感测、通信、处理、收集数据，然后通过互联网将数据传输给监测者进行进一步分析，是通过无线通信方式形成的一个多跳自组织网络，可用于大规模物联网应用。由于其传感器通过无线方式通信，所以位置可以随时更改，非常灵活。WSN的覆盖优化问题可以描述为在规定的监测区域内，保证传感器网络连通情况下的节点部署问题。
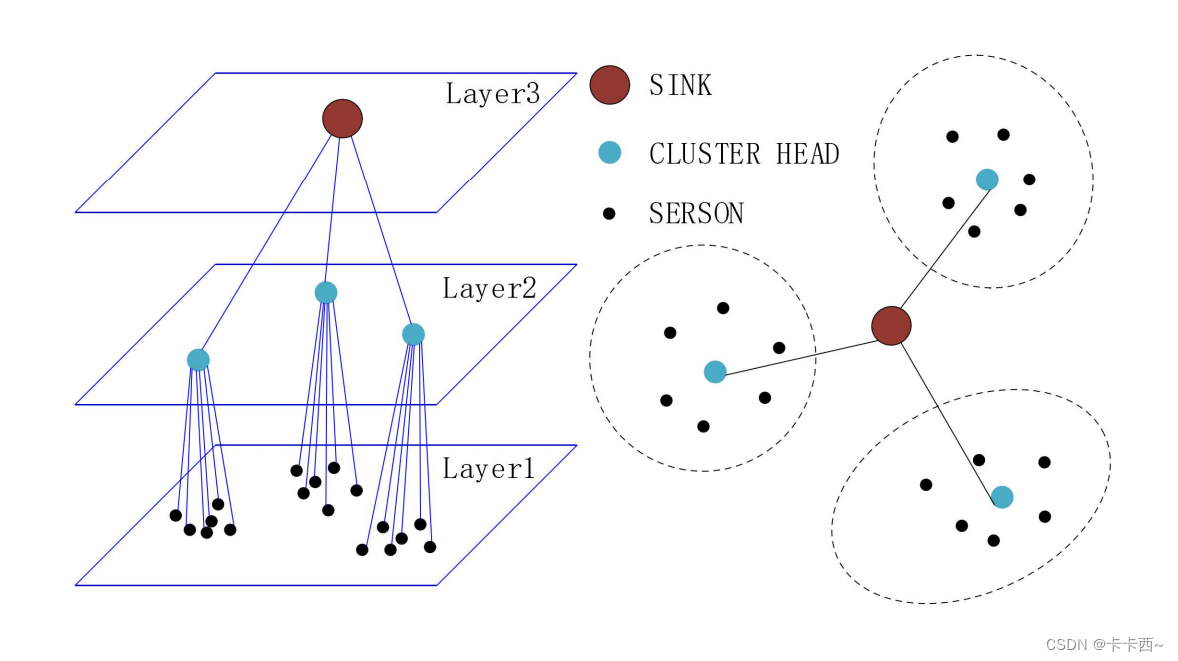
- WSNs系统包括三部分： （1） 传感器节点本质是一个小型嵌入式系统，由传感器模块、处理器模块、无线通信模块、能量供应模块四部分组成，既可充当数据发送者也可充当中间路由者。负责收集本地信息和处理数据（存储，管理，融合），向其它传感器节点传输数据，与其它传感器节点协作完成一些任务； （2）汇聚节点负责将传感器节点收集到的数据汇聚到一起，再通过无线通信方式传送到管理节点； （3）管理节点是终端监测平台，用户通过管理节点对WSNs进行配置管理，发布监测任务及收集监测数据等。传感器节点监测的数据经过多跳后传输到汇聚节点，然后通过互联网或卫星到达管理节点。WSN可以被定义为下图具有三层的二维网络，最底层为分布在目标区域的传感器节点，有若干个簇，每个簇都有一个簇头（汇聚节点），这些簇头组成了中间层，每个传感器节点都可以直接与它们的簇头通信，簇头可以与顶层的Sink节点（管理节点）通信。每轮数据传输分为两个阶段：在簇的建立阶段中，每一轮都先选择最佳部署解决方案 I ，再选举簇头（每一轮的簇头都可以不一样），然后分组（非簇头节点计算与所有簇头的通信消耗，选最低的簇头）。在传输数据阶段中，簇头收集簇内传感器节点的数据，然后发送给sink节点。
- WSNs应用：军事航空，环境监测，医疗保健，工业制造，智慧交通，智慧家庭，智慧城市，救灾等。
- 存在的问题：覆盖盲区（不够），节点冗余（太多，浪费），处理能力、存储能力、通信能力较弱
2 相关分类
2.1 按节点部署方式分类
- 静态WSN：在网络运行前就确定节点的位置，部署后不再做移动。
- 动态WSN：所有节点（传感器节点和汇聚节点）都可移动，根据网络的具体需求（网络扩展、故障修复等）进行动态部署。
- 混合WSN：多数固定节点 + 少数移动节点，主要解决的是移动节点的自我调整部署问题。
2.2 按覆盖目标分类
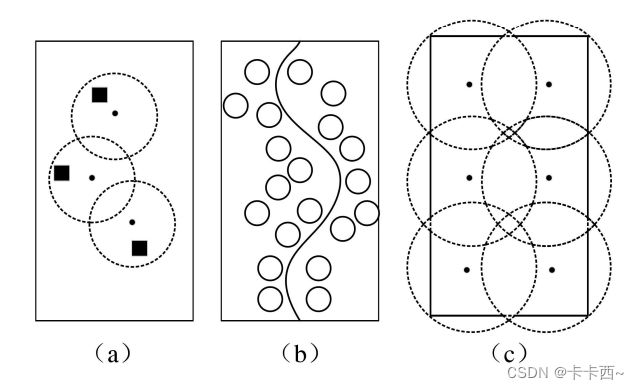
- 点覆盖：如图（a）又叫目标覆盖，图（a）圆点为传感器节点，方块为监测目标，要求每个目标至少被一个传感器节点覆盖。
- 栅栏覆盖：如图（b），要求传感器节点监测移动目标的运动轨迹。主要用于国防边境的非法越境者探测，军事战场敌军入侵侦查，环境保护中的物种迁徙监测等。
- 区域覆盖：如图（c），要求用尽可能少的传感器节点尽量覆盖整个目标区域。 主要用于森林火灾预警，湖泊水面水质监测等大规模应用环境，或者煤矿巷道，工厂车间，仓库等受限区域的安全监控应用。
2.3 按网络中的传感器类型分类
- 同构WSNs：传感器类型一样，网络同质；
- 异构WSNs：传感器类型和感知能力都不一样；在未来的智能城市中，WSNs将是异构的。
2.4 传感器种类
- 全向传感器：二维为圆盘，三维为球，只有覆盖和非覆盖，非0即1，一般基于确定性布尔模型，在实际应用中，各种能力会随着距离增加而降低；
- 定向传感器：各种能力会随着距离和角度增加而降低。
2.5 地形分类
- 平面：二维的；
- 马鞍地形：三维的，如图a；
- 多峰地形：三维的，如图b，比前两种更复杂。
在三维环境中，无线信号会沿着传输路径被反射、散射、衍射。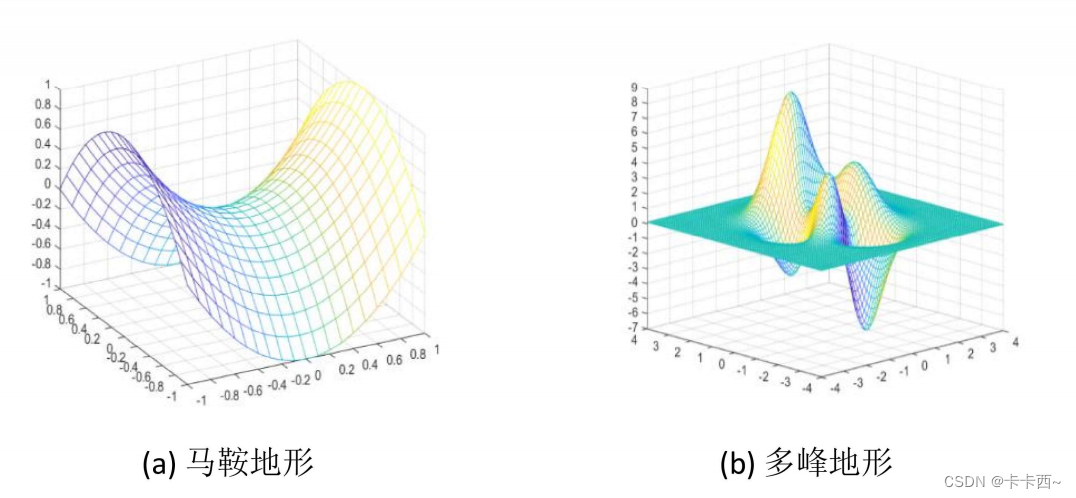
3 评价指标
3.1 覆盖率
网络覆盖率越大，部署效果越好。
3.2 均匀度
传感器节点的均匀度指标E为所有传感器节点间的距离标准差的和的均值，计算如下：
3.3 节点移动距离
各个节点都要从初始化位置移动到算法找到的最佳位置，移动距离越小，消耗的能量越小；
3.4 连通性
节点之间要互相传递信息，所以应该保证网络的连通性。
建立有向图邻接矩阵
M
v
M_v
Mv，如果两个传感器节点 i 和 j 的距离不超过 i 的通信半径
R
i
c
R_i^c
Ric，说明 i 可以给 j 传输信息，对应
M
v
[
i
]
[
j
]
=
1
M_v[i][j]=1
Mv[i][j]=1。最后用矩阵幂算法进行计算，如果矩阵中存在 0 ，则说明网络不连通。
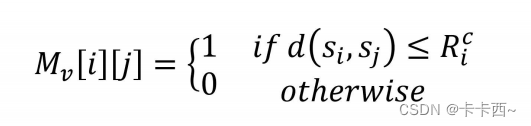
3.5 能耗和寿命
传感器节点电池不可充电，所以应该在保证覆盖率最大的前提下，尽量降低能量损失，增加网络寿命。
具体用什么样的能量消耗模型由网络使用的路由协议决定，比如在LEACH协议中，方案 I 的能量消耗
E
(
I
)
E(I)
E(I)包括信息通信消耗（数据传输和接收）、数据聚合消耗和激活部署方案 I 中的节点，计算如下：
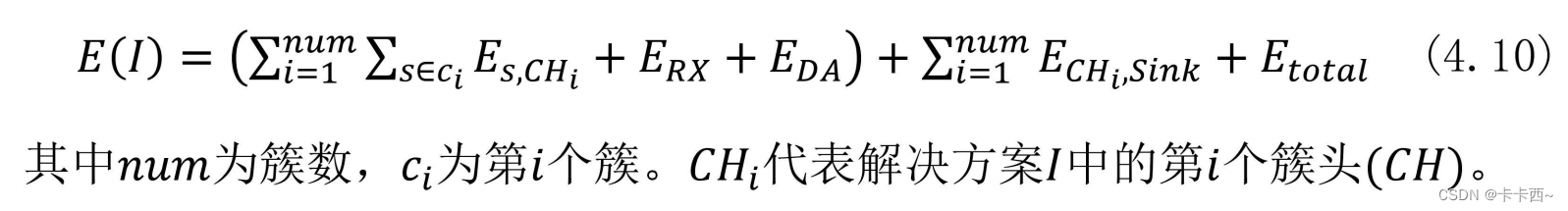
而能耗也与选择的数据传输模型有关，常用的数据传输模型有自由空间模型、多径衰落模型，这两种模型都取决于发送节点与接收节点的距离。一般情况下，对传输距离 d 和阈值进行比较，d 小于阈值时，使用自由空间模型，否则使用多径衰落模型，传输 l bit数据的能量消耗计算如下：
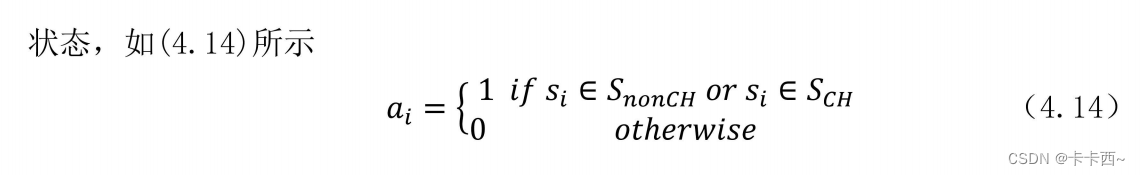
3.6 信息传输数量
在保证覆盖率最大的前提下，传感器节点向簇头传输的数据越多，越能真实反映监测区域的情况，所以应该尽可能传输较多的数据；
3.7 算法复杂度
越低越好。
二、相关模型
1 传感器节点感知模型
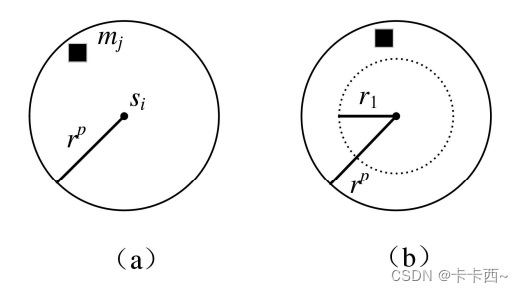
1.1 布尔感知模型（图a）
也叫二元感知模型，是一种理想的感知模型，节点在传输信号时能力不会随着距离增加而降低，适用于节点监测半径较小时，忽略信号在传输过程中的衰减。它在基础理论推导中经常使用，在实际生活中使用较少。
一个传感器节点对一个像素点的感知概率计算：如图（a），圆点
s
i
s_i
si是传感器节点，方块
m
j
m_j
mj是监测目标，
r
p
r^p
rp是
s
i
s_i
si的感知半径，这个圆盘是节点
s
i
s_i
si的感知区域。如果监测目标
m
j
m_j
mj在节点
s
i
s_i
si的感知区域内，则认为
m
j
m_j
mj被
s
i
s_i
si覆盖。（传感器节点的通信半径
r
c
r^c
rc一般大于等于
2
r
p
2r^p
2rp）。
很显然，我们必须计算
m
j
m_j
mj与
s
i
s_i
si之间的距离。两点之间的距离有很多种，如果是欧氏距离，且在二维平面，那么两点之间的距离
d
(
s
i
,
m
j
)
=
(
x
i
−
x
j
)
2
+
(
y
i
−
y
j
)
2
d(s_i,m_j)=\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}
d(si,mj)=(xi−xj)2+(yi−yj)2，如果是三维空间，再加个坐标 z 就好了。
进而得到
m
j
m_j
mj被
s
i
s_i
si感知的概率为：
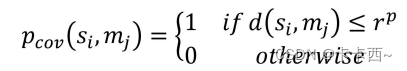
这个非1即0的概率真的很“布尔”。
所有传感器节点对一个像素点的联合感知概率计算：监测节点
m
j
m_j
mj的联合感知概率
C
p
(
s
a
l
l
,
m
j
)
C_p(s_{all},m_j)
Cp(sall,mj)计算如下：
C
p
(
s
a
l
l
,
m
j
)
=
1
−
∏
i
=
1
N
(
1
−
p
c
o
v
(
s
i
,
m
j
)
)
C_p(s_{all},m_j)=1-\prod_{i=1}^{N}(1-p_{cov}(s_i,m_j))
Cp(sall,mj)=1−i=1∏N(1−pcov(si,mj))
只要有一个
s
i
s_i
si可以感知到
m
j
m_j
mj，
p
c
o
v
(
s
i
,
m
j
)
就为
1
p_{cov}(s_i,m_j)就为1
pcov(si,mj)就为1，那么后面连乘这部分就为0，最后的联合感知概率就为1。
二维平面覆盖率计算:设 N 个同构传感器节点集合
S
=
{
s
1
,
s
2
,
.
.
.
,
s
N
}
S=\{s_1,s_2,...,s_N\}
S={s1,s2,...,sN}，K个监测节点集合
M
=
{
m
1
,
m
2
,
.
.
.
,
m
K
}
M=\{m_1,m_2,...,m_K\}
M={m1,m2,...,mK}，矩形监测区域面积为
L
×
W
m
2
L×Wm^2
L×Wm2，将监测区域划分成
L
×
W
L×W
L×W个网格，每个网格面积为
1
m
2
1m^2
1m2，监测节点位于网格的中心点，则覆盖面积 = 所有监测点的联合感知概率累加之和，覆盖率为 覆盖面积 / 监测区域面积。
覆盖率
C
r
C_r
Cr计算如下：
C
r
=
∑
j
=
1
K
C
p
(
s
a
l
l
,
m
j
)
L
×
W
C_r=\frac{\sum_{j=1}^{K}C_p(s_{all},m_j)}{L×W}
Cr=L×W∑j=1KCp(sall,mj)
1.2 概率感知模型（图b）
节点在传输信号时能力会随着距离增加而降低，可以较客观反映现实生活中网络部署环境。
一个传感器节点对一个像素点的感知概率计算：如图（b），它在（a）的基础上多了一个半径
r
1
r_1
r1，我们首先也是先计算
m
j
m_j
mj与
s
i
s_i
si之间的距离，进而得到
m
j
m_j
mj被
s
i
s_i
si感知的概率：
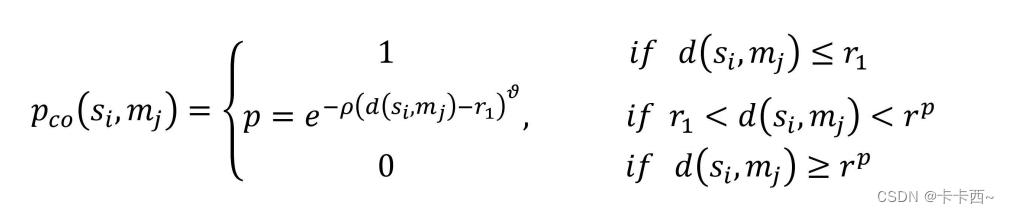
这个很好理解，如果两点间距离小于
r
1
r_1
r1，表示
m
j
m_j
mj肯定可以被
s
i
s_i
si感知；如果两点间距离在
r
1
r_1
r1与
r
p
r^p
rp之间，表示
m
j
m_j
mj有可能被
s
i
s_i
si感知，这个可能性有多大？由第二个子式计算得到。该子式中的参数
ρ
\rho
ρ和
θ
\theta
θ由传感器属性和监测环境决定。
2 簇头选择模型
2.1 江西理工
每个传感器节点被选为簇头的概率为p
c，如果该传感器节点随机生成值小于簇头选举阈值
H
(
i
)
∈
[
0
,
1
]
H(i)\in[0,1]
H(i)∈[0,1]，该节点选为当前轮的簇头。
H
(
i
)
H(i)
H(i)计算如下：
3 虚拟力算法
4 三维相关算法
- 曲面面积的计算： 对于三维空间来说，监测区域是曲面。一种简单的计算曲面表面积的方法为：先将曲面映射到二维平面中，然后将平面划分为好多面积相同的小网格，然后用曲面积分公式计算每个小网格对应的小曲面的表面积，最后加起来就得到了整个曲面的表面积。
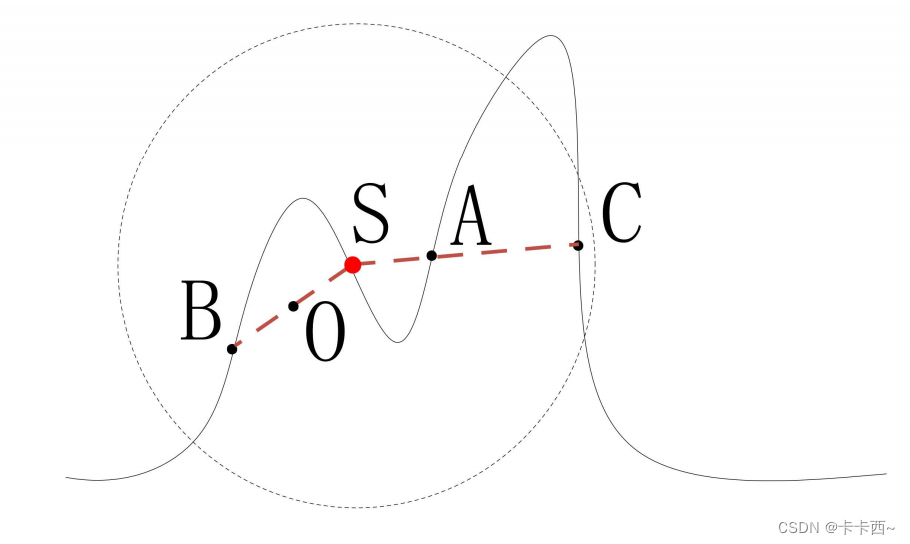
- 三维感知盲区： 在三维空间内，由于障碍物遮挡，有些目标虽然在传感器节点的感知范围内，但也感知不到，比如下图的点 C。 判断两点之间是否存在遮挡，有一种简单的方法为将 SC 连接起来，得到该范围内的曲面方程，然后求零点，如果存在零点，说明存在遮挡。比如点 A 就是一个零点。
本文转载自: https://blog.csdn.net/weixin_46838605/article/details/128243600
版权归原作者 卡卡西~ 所有， 如有侵权，请联系我们删除。
版权归原作者 卡卡西~ 所有， 如有侵权，请联系我们删除。