🚀个人主页:欢迎访问Ali.s的首页
⏰ 最近更新:2022年8月24日
⛽ Java框架学习系列:【Spring】【SpringMVC】【Mybatis】
🔥 Java项目实战系列:【飞机大战】【图书管理系统】
🍭 Java算法21天系列:【查找】【排序】【递归】
⛳ Java基础学习系列:【继承】【封装】【多态】
🏆 通信仿真学习系列:【硬件】【通信】【MATLAB】
🍄 个人简介:通信工程本硕🌈、Java程序员🚴。目前只会CURD😂
💌 点赞 👍 收藏 💗留言 💬 都是我最大的动力💯


文章目录
前言
在前面一文中已经详细且生动的解释了傅里叶变换和傅里叶级数的内容,【通信原理】揭开傅里叶级数与傅里叶变换的神秘面纱,而在今天这篇中有些公式你可能会产生疑惑,基本上需要用到傅氏变化的知识,可能需要你自行了解一下过程或参考一下上一篇文章的内容并加以理解。
一、确知信号的分类
在通信系统中,可以按照不同的标准将通信信号划分为不同的类型,常见的分类确知信号与随机信号、周期信号与非周期信号、能量信号与功率信号等。
1、确知信号与随机信号
确知信号是指在任何时间其取值都是确定和可预知的信号,一般都可以使用数学表达式对信号进行描述,比如基本参数确定的正弦信号就是一个确知信号。而与确知信号对立的就是随机信号,随机信号是指取值不确定且不能事先预知的信号,自然是不能使用确定的数学表达式来衡量,需要在一段时间内进行观察,统计出一定的统计规律,寻找它的统计特性,通常是看做一个随机过程。随机过程的内容比较复杂,对数学要求比较高,在后续文章会单独分析。
2、周期信号与非周期信号
周期信号:每隔一定的时间间隔按照相同的过来重复且无始无终的信号。
非周期信号:不满足周期信号的特征的其它信号。
连续周期信号
s(t)
满足: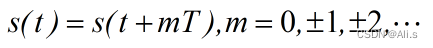
离散周期信号
s(n)
满足: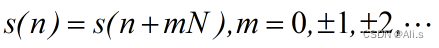
式中的
T
和
N
表示该信号的最小正周期。
3、能量信号与功率信号
能量信号和功率信号是信号处理和通信研究的最多的信号,有许多的特性和结论都是根据它们推倒或者演变得到。将信号
s(t)
施加于1Ω电阻上,它所消耗的瞬时功率为
|s(t)|^2
,在无限长的区间上的能量E和平均功率P定义为: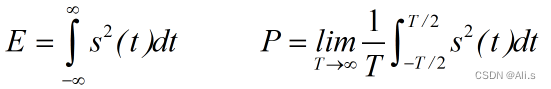
能量信号:能量为有限值,功率趋向于0的信号,常见的有单个矩形脉冲信号等。
功率信号:功率为有限值,能量为无穷大的信号,常见的有周期信号等。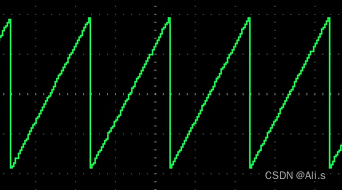
二、确知信号频域性质
1、功率信号频谱
周期性功率信号频谱被定义为: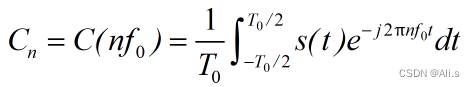
对于物理可实现的实信号,正频率部分和负频率部分间存在复数共轭关系,即:
而由上式可知,功率信号的频谱特征为模偶对称,相位奇对称: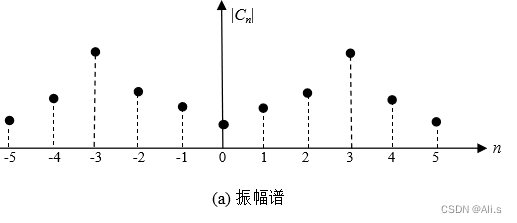
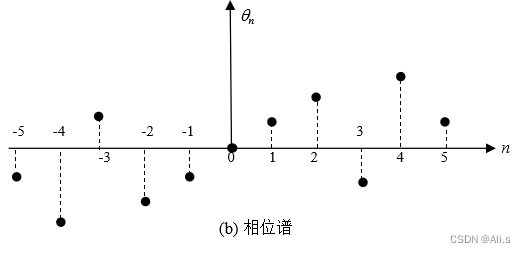
2、能量信号频谱密度
能量信号的频谱密度被定义为
S(f)
,对能量信号
s(t)
做傅里叶变换得到信号的频谱密度: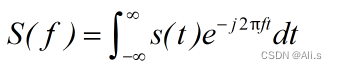
S(f)
与
Cn
的主要区别是前者是连续谱,而后者是离散谱,前者的单位是
V/HZ
,后者的单位是
V
,当信号为实能量信号时,负频谱和正频谱的模偶对称,相位奇对称:
单位冲激函数的频谱密度为
1
,通过求其傅里叶变换可以轻松得到,从极限的方向看,函数可以用抽样函数的极限表示: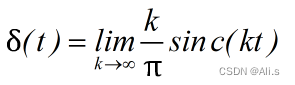
式中
k
越大、振幅越大、波形零点的间隔越小、波形振荡的衰减越快。
设一个余弦波的表示式为
s(t)=cos2πf0t
,则其频谱密度
S(f)
可以写为: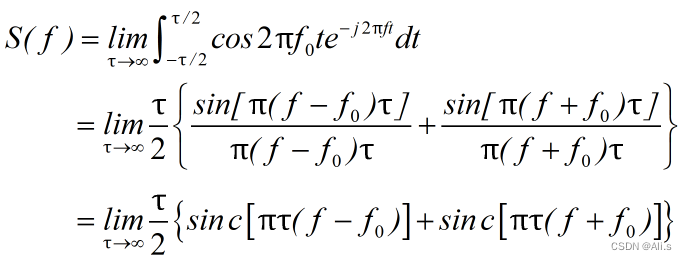
根据冲击信号的极限定义,可将其频谱改写为: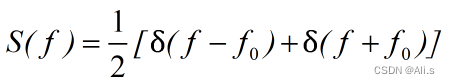
引用了冲激函数就能把频谱密度的概念推广到功率信号上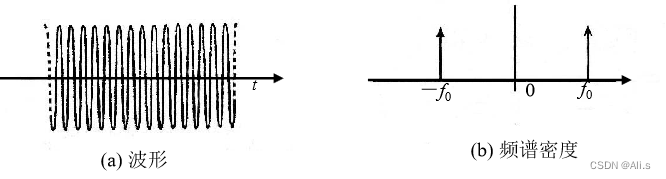
3、能量信号的能量谱密度
能量信号的能量谱密度是指用密度的概念表示信号能量在各频率点的分布情况,在能量谱中对频率进行积分,就可以得到信号的能量。根据巴塞伐尔定理可知: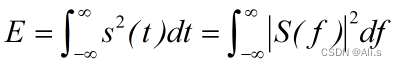
由于信号
s(t)
是一个实函数,所以
|S(f)|
是一个偶函数, 因此上式可以写成: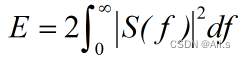
能量谱反映了能量信号的能量随频率的变化情况,是原信号的傅里叶变换绝对值的平方,单位为
焦耳/HZ
。
4、功率信号的功率谱密度
由于功率信号的能量无穷,所以无法计算功率信号的能量谱密度,但是可以求它的功率谱密度。所以将把信号
s(t)
截断为长度为
T
的一截短信号,表示为
sT(t)
,此时截断信号就是能量信号,可以用傅里叶变换求出其能量谱密度 ,由巴塞伐尔定理可知: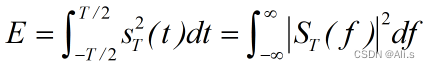
最后将能量谱密度除以长度
T
,采用极限的思想就得到了功率谱密度: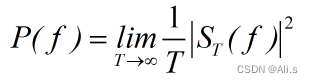
功率谱密度反映了功率信号的功率随频率的变化情况,在功率谱密度中对频率进行积分就得到了功率信号的功率,功率信号的计算就是信号傅里叶变换的平方与区间长度的比值。
三、确知信号时域性质
1、能量信号自相关函数
能量自相关函数是指信号本身与其一段时间内的延时信号的乘积的积分,自相关函数与时间
t
无关,只和时间差
τ
有关,其定义式为: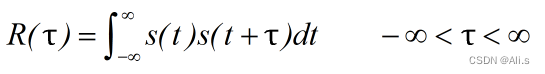
当时间延时
τ = 0
时,
R(0)
等于信号的能量: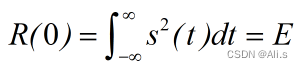
根据能量谱的关系,自相关函数和其能量谱密度是一对傅氏变换: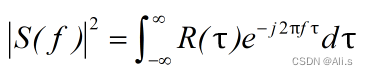
2、能量信号互相关函数
互相关函数是指信号1与信号2在一段时间内的延时信号的乘积的积分,互相关函数与时间
t
无关,只和时间差
τ
有关,其定义式为: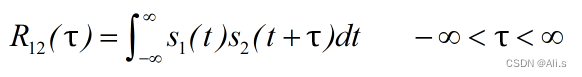
并且互相关函数与两个信号相乘的次序有关,由于次序的不同,会有一个反转的过程,但两个信号的互相关性应该是不变的,与信号的时域变换应当没有关系,所以: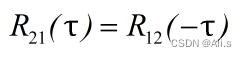
其证明过程也非常简单,利用积分的性质就可以完成: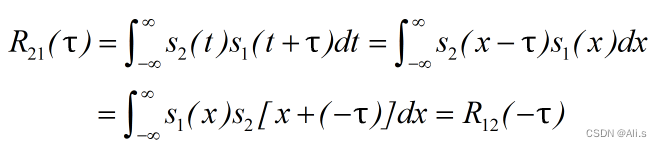
同样的思路,可以得到互相关函数和互能量谱密度是一对傅里叶变换:

总结
本文从通信系统中确知信号出发,分析了能量信号、功率信号的关系与性质,对确知信号在频域中的四种性质:频谱、频谱密度、能量谱密度、功率谱密度进行推导分析,对确知信号在时域中的特性:自相关函数、互相关函数的内容进行研究分析,发现与傅里叶变换精密相关。对确知信号总体有一个新的认识。
版权归原作者 Ali.s 所有, 如有侵权,请联系我们删除。