1.小故事
一家金融科技公司,公司的首席执行官找到团队提出了一个紧迫的问题:“我们如何提前知道哪些客户可能会违约贷款?” 这让团队陷入了沉思,经过激烈讨论团队中的数据分析师提议:“我们可以尝试使用逻辑回归来预测客户的违约风险。”
团队成员们听后都点头表示赞同,决定尝试这个方法,于是他们开始忙碌地收集客户数据,包括信用评分、收入情况、贷款历史记录等。数据堆积如山,他们耐心地清洗、整理,他们准备用这些数据来“喂养”他们的逻辑回归模型。经过不懈的努力,模型终于建立起来了,它就像一个刚刚诞生的智能生命,开始从数据中学习,逐渐成长。
团队紧张地观察着模型的每一次迭代,每一次优化。终于,在一次次的试验和改进后,模型预测的准确率越来越高。从此,这家金融科技公司利用这个逻辑回归模型,在贷款审批过程中,更加精准地评估了客户的信用风险。公司因此大大降低了坏账率,业绩也随之飙升。而那个逻辑回归模型,也在金融科技领域绽放着它的光芒。
2.逻辑回归
逻辑回归(Logistic Regression)是一种用于处理二分类问题的统计学习方法。虽然其名字中带有“回归”,但它其实是一种分类算法,用于处理二分类或多分类问题,主要用于预测数据实例属于某个特定类别的概率。它的基本原理是:对于给定的输入变量(也称为特征),逻辑回归模型会输出一个介于0和1之间的概率值,这个概率值表示样本属于某个特定类别的可能性。
逻辑回归具有以下优点:
直观性:逻辑回归模型简单直观,易于理解。它基于线性回归模型,通过Sigmoid函数将线性回归的连续输出转换为0到1之间的概率值,从而实现对二分类问题的建模。
易实现性:逻辑回归的计算过程相对简单,容易编程实现。许多编程语言和机器学习库都提供了逻辑回归的实现,使得开发者可以快速地构建和训练模型。
计算效率高:逻辑回归的训练过程通常较快,能够快速地处理大量数据。这使得逻辑回归在处理大规模数据集时具有较高的效率。
对缺失值和异常值不敏感:逻辑回归对数据的缺失值和异常值具有一定的鲁棒性。在训练过程中,逻辑回归可以通过正则化等方法来减少过拟合现象,从而提高模型的泛化能力。
稳定性:逻辑回归模型通常具有较好的稳定性,即在不同的数据集上训练得到的模型差异较小。这使得逻辑回归在实际应用中具有更好的可靠性和一致性。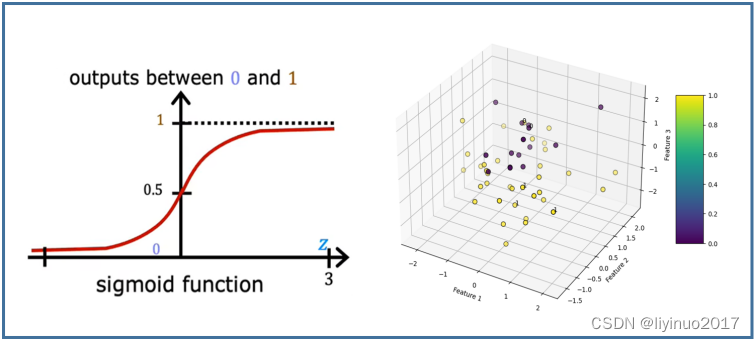
逻辑回归在人工智能医疗诊断中的应用非常广泛,其通过处理和分析医疗数据,为医生提供决策支持,提高诊断的准确性和效率。例如,通过收集个体的年龄、性别、家族病史、生活习惯、生理指标(如血压、血糖、血脂等)等数据,结合大量的患病数据,可以建立逻辑回归模型来评估个体在未来一段时间内患病或遭受某种不良事件的风险。
逻辑回归也广泛应用于人工智能电商推荐中,如从这用户的基本信息(性别、年龄、地域等)、浏览商品的类别、价格、品牌等。使用逻辑回归模型,根据这些特征来预测用户可能对哪些商品感兴趣。
3.依赖工具库
本文中的实战代码依赖了4个工具库:scikit-learn、pandas、matplotlib、numpy 。
Scikit-learn(也称sklearn)是一个针对Python编程语言的免费软件机器学习库。它提供了各种分类、回归和聚类算法,包含支持向量机、随机森林、梯度提升、k均值和DBSCAN等。
Matplotlib是一个Python的2D绘图库,可以绘制各种图形,如折线图、直方图、功率谱、条形图、散点图等。
Pandas是一个基于NumPy的Python数据分析包,提供了高性能的数据结构和数据分析工具。提供了Series(一维数组)和DataFrame(二维表格型数据结构)两种主要的数据结构。支持数据清洗、转换、筛选、排序、分组、聚合等操作。
Numpy是Python的一个开源数值计算扩展,用于存储和处理大型矩阵。提供了N维数组对象(ndarray),支持大量的维度数组与矩阵运算。提供了数学函数库,支持线性代数、傅里叶变换等操作。
Seaborn建立在Matplotlib的基础之上,但提供了更高级别的API,它提供了多种常用的可视化方法,如散点图、折线图、直方图、核密度估计图、箱线图、热点图、线性回归图等。
首先确保编程环境已正确搭建,若编程环境尚未搭建完毕,建议参照《从零入手人工智能(2)——搭建开发环境》,文章链接如下:
https://blog.csdn.net/li_man_man_man/article/details/139537404?spm=1001.2014.3001.5502
4.程序流程
本文中的代码实现旨在展示逻辑回归算法的核心功能,入门版程序不超过30行代码。这个简短的代码片段实则包含了人工智能算法开发的重要三板斧:数据预处理、模型构建与训练、模型验证。
数据预处理阶段:代码需要能够处理原始数据,可能包括数据的加载、转换、归一化等步骤,以确保输入到模型中的数据是符合算法要求的。
模型构建与训练阶段:涉及到了使用逻辑回归算法建立预测模型,并通过训练数据来优化模型的参数。
模型验证阶段:用于评估训练好的模型在数据预测上的准确性。绘制预测结果与实际结果之间的对比图等可视化手段。
5.入门例程
实例1
STEP1:自动生成了一组数据集,其中训练数据X包含两个特征数据。随后基于这两个特征之间的线性关系,通过一个预设的转换函数生成了目标变量Y。
STEP2:利用LogisticRegression方法建立逻辑回归模型,接着我们使用训练数据X和对应的Y来训练逻辑回归模型。模型训练完成后,我们采用合适的评估指标(如准确率)来评估模型的性能。
STEP3:直观地展示模型的预测效果,进行可视化分析。通过绘制决策边界,我们能够清晰地看到模型如何根据输入特征X的值来预测目标变量Y的分类。此外我们还可能绘制视化图表。
代码如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
# 自动生成数据
np.random.seed(0)
n_samples =100
X = np.random.randn(n_samples,2) # 生成2个特征的数据
# 创建一个简单的线性可分标签
y =(X[:,0]>0).astype(int)
# 数据标准化
scaler =StandardScaler()
X_scaled = scaler.fit_transform(X)
# 训练逻辑回归模型
model =LogisticRegression(solver='liblinear', max_iter=1000)
model.fit(X_scaled, y)
# 评估模型准确性
y_pred = model.predict(X_scaled)
accuracy =accuracy_score(y, y_pred)print(accuracy)
# 可视化结果
plt.figure(figsize=(10,6))
# 绘制散点图,根据标签上色
colors =['red'if label ==0else'blue'for label in y]
plt.scatter(X_scaled[:,0], X_scaled[:,1], c=colors, edgecolor='k', s=50)
# 创建一个网格来评估模型
x_min, x_max = X_scaled[:,0].min()-.5, X_scaled[:,0].max()+.5
y_min, y_max = X_scaled[:,1].min()-.5, X_scaled[:,1].max()+.5
h =(x_max /(len(X_scaled)-1))/20
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 绘制决策边界
plt.contourf(xx, yy, Z, alpha=0.4)
plt.contour(xx, yy, Z, colors='k', linestyles='--', levels=[.5])
# 在每个数据点旁边添加标签值(可选)
for i, txt in enumerate(y):
plt.text(X_scaled[i,0], X_scaled[i,1], txt, ha='center', va='bottom', fontsize=8)
# 设置坐标轴标签和标题
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Logistic Regression with 2 features')
# 显示图形
plt.show()
代码运行结果如下: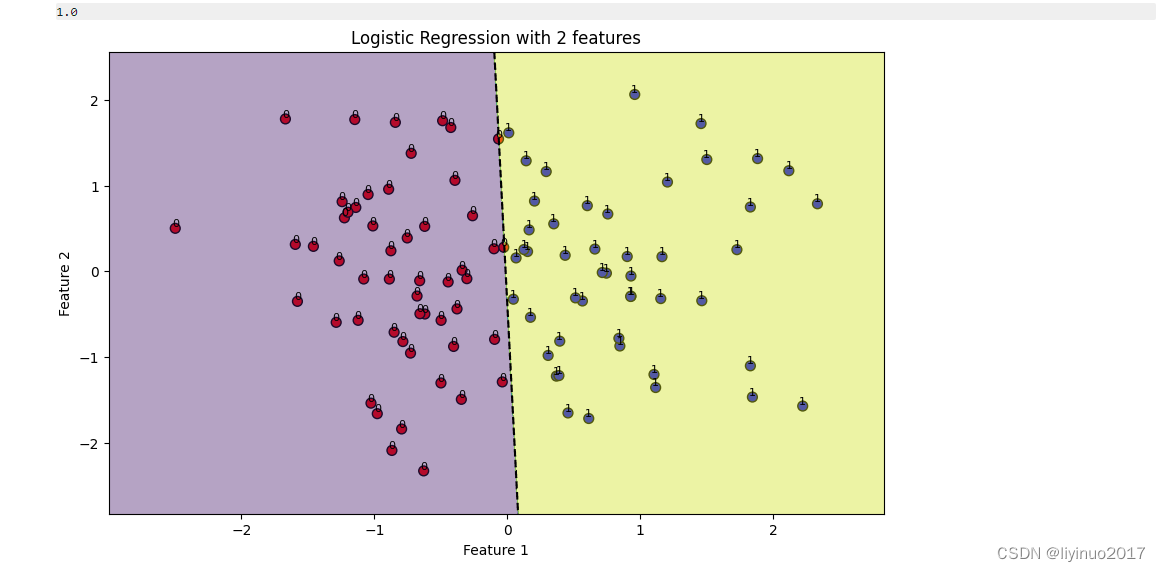
实例2
本实例与实例1基本一样,唯一的区别是:程序自动生成的训练数据X包含三个明确的数值特征,最后显示的是一个3D的可视化图表。
代码如下:
import numpy asnp
import matplotlib.pyplot aspltfrom sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from mpl_toolkits.mplot3d import Axes3D
from sklearn.metrics import accuracy_score
# 自动生成数据
np.random.seed(0)
n_samples =100
X = np.random.randn(n_samples,3) # 生成3个特征的数据
# 创建一个非线性可分的标签
y =(X[:,0]**2+ X[:,1]**2-5*X[:,2]>0).astype(int)# 划分数据集为训练集和测试集(此处仅使用训练集)
X_train, _, y_train, _ =train_test_split(X, y, test_size=0.5, random_state=42)# 数据标准化
scaler =StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)# 训练逻辑回归模型
model =LogisticRegression(solver='liblinear', max_iter=1000)
model.fit(X_train_scaled, y_train)
y_pred = model.predict(X_train_scaled) # 预测标签
accuracy = accuracy_score(y_train, y_pred)print(accuracy)# 绘制数据点,根据标签上色
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')
sc = ax.scatter(X_train_scaled[:,0], X_train_scaled[:,1], X_train_scaled[:,2], c=y_train, cmap='viridis', edgecolor='k', s=50)# 添加坐标轴标签和标题
ax.set_xlabel('Feature 1')
ax.set_ylabel('Feature 2')
ax.set_zlabel('Feature 3')
ax.set_title('Logistic Regression with 3 features')# 随机选择几个点并显示它们的标签值 for i, txt inenumerate(y_train[:5]): # 只显示前5个点的标签值作为示例
ax.text(X_train_scaled[i,0], X_train_scaled[i,1], X_train_scaled[i,2], txt, color='black')# 显示颜色条
fig.colorbar(sc, ax=ax, shrink=0.5, aspect=5)# 显示图形
plt.show()
代码运行结果如下: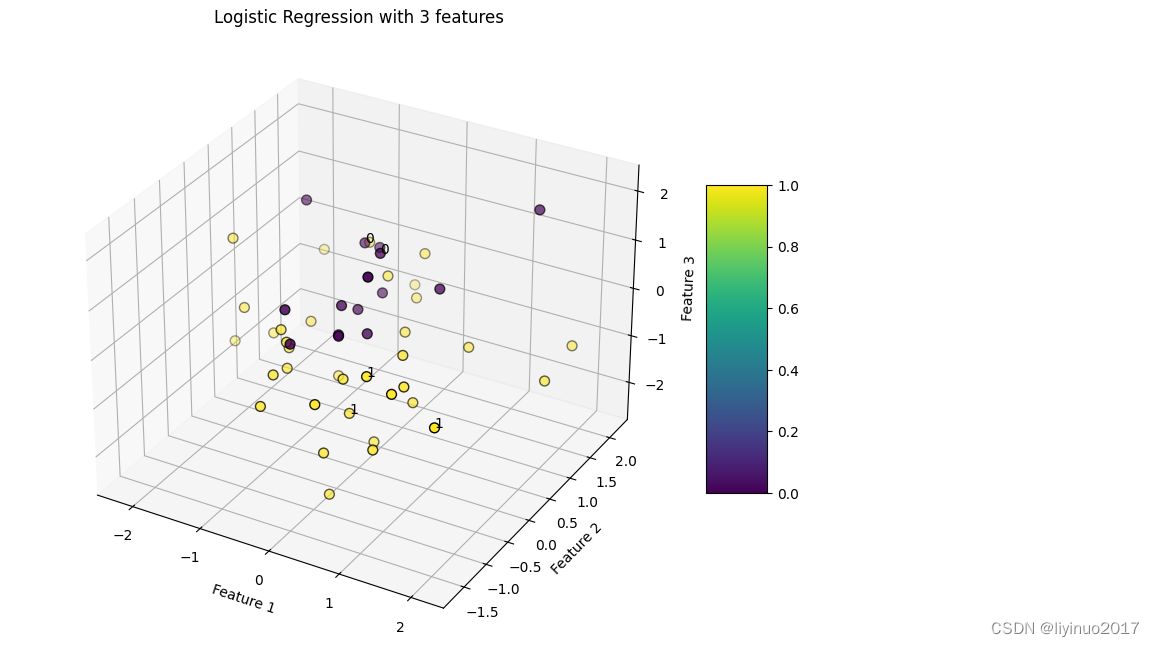
6.进阶实战(乳腺癌检测)
本实战项目是使用威斯康星州癌症乳腺数据集利用逻辑回归模型预测癌症的良性和恶性。这些数据由威斯康星大学的研究人员捐赠,包括乳腺肿块细针抽吸物的数字化图像测量结果。癌症数据包括569例癌症活组织检查,每个活组织检查具有32个特征。一个特征是识别号,另一个是癌症诊断,30是数值实验室测量。诊断代码为“M”表示恶性,“B”表示良性。
为了减小数据复杂度,我们在威斯康星州癌症乳腺原始数据上进行了数据裁剪,只保留了12列数据。处理后的数据如下
569条样本,共12列数据,第1列用语检索的id(在数据计算中无用),第2列数据为诊断结果为“M”表示恶性,“B”表示良性,后面的10列分别是与肿瘤相关的验室测量的特征数据。
(希望获取源码和数据表的朋友可以在评论区留言!!!)
程序流程是:数据预处理、模型构建与训练、模型验证。
数据预处理:首先加载数据表breast-cancer-wiscons.csv ,随后将数据表中的diagnosis列赋值给 Y,同时将Y转换成0和1,最后将去掉diagnosis列和id列去掉后的数据赋值给X。完成数据赋值后,可视化X中10个特征变量之间的关系,代码运行如下图。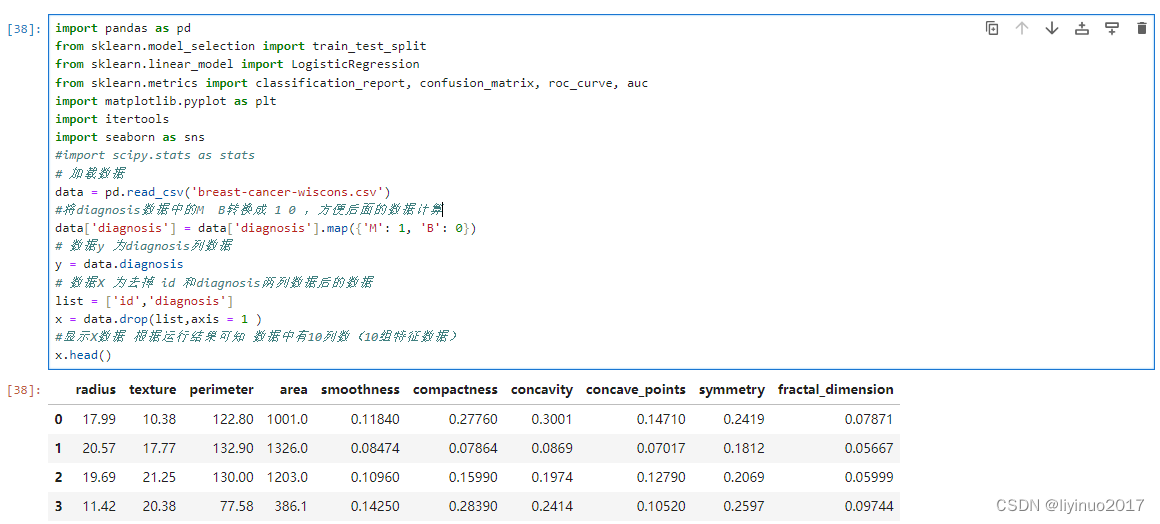

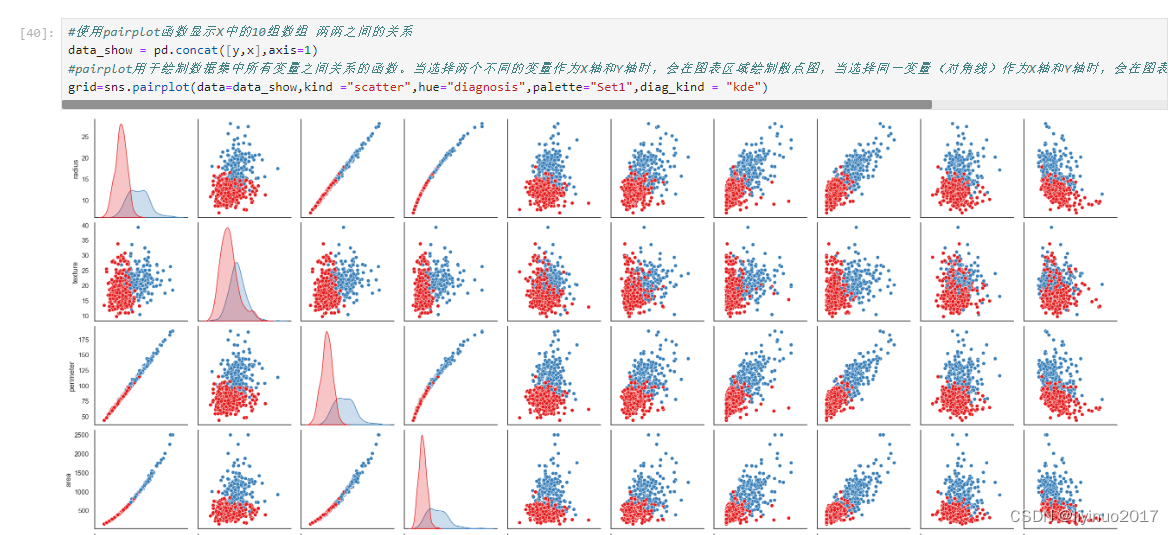
模型构建与训练:完成数据处理后,建立模型,训练模型并预测预测数据
模型验证:完成模型训练后,进行数据预测,最后我们使用混淆矩阵和ROC曲线可视化数据准确性。
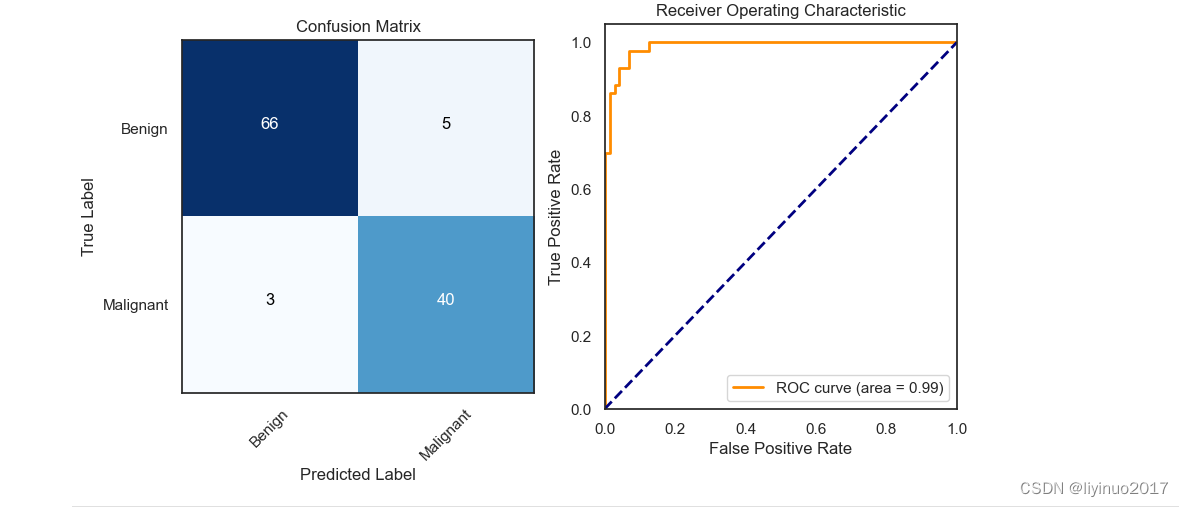
希望获取源码和数据表的朋友可以在评论区留言!!!
希望获取源码和数据表的朋友可以在评论区留言!!!
希望获取源码和数据表的朋友可以在评论区留言!!!
创作不易希望朋友们点赞,转发,评论,关注!
您的点赞,转发,评论,关注将是我持续更新的动力!
CSDN:https://blog.csdn.net/li_man_man_man
今日头条:https://www.toutiao.com/article/7149576260891443724
版权归原作者 liyinuo2017 所有, 如有侵权,请联系我们删除。
