一、主观评价
1、层次分析法(AHP)
①应用场景
1、最佳方案选取
2、评价类问题
3、指标体系的优选
②步骤
1、将问题条理化、层次化,构造出一个有层次的结构模型。层次分为三层:目标层、准则层、方案层。
2、比较同一层次元素对上一层次同一目标的影响,从而确定它们在目标中所占的比重。采用两两比较的方法,求出他们对于同一个目标的重要性的比例标度,标度等级为1,2,...,9,1/2,1/3,...1/9。得到两两比较判断矩阵。
1--9标度的含义:
1--两个元素同等重要 3--前者稍重要
5--前者明显重要 7--前者强烈重要
9--前者极端重要
2,4,6,8为上述判断的中间值
3、在单一准则下计算元素相对排序权重,以及判断矩阵一致性检验。
4、计算方案层中各元素对于目标层的总排序权重,从而确定首选方案。
③模型实现
题目:对 2017 年各省生态环境与经济交互状况进行合理的评价
应用层次分析法解决问题时,首先要将问题条理化、层次化,构造出一个有层次的结构模型。
这些层次可分为三类:
最高层:经济对环境的影响。
中间层:GDP、人口、地方财政支出、地方财政收入以及居民收支情况。
最底层:严重、轻度、基本无影响。
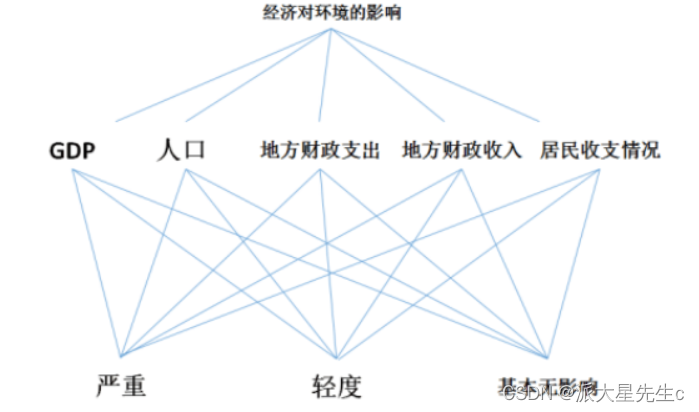
结构图如果所示
建立准则层判断矩阵
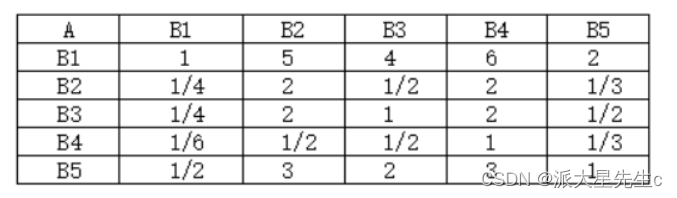
** 建立方案层判断矩阵**

对判断矩阵的一致性检验。
(i)计算一致性指标 CI

(ii)查找相应的平均随机一致性指标 RI 。用随机方法构造 500 个样本矩阵:随机地从 1~9
及其倒 数中抽取数字构造正互反矩阵,求得最大特征根的平均值 max λ',并定义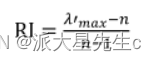
(ⅲ)计算一致性比例 CR
当 CR<0.1 时,认为判断矩阵的一致性是可以接受的,否则对应判断矩阵作适当修正。
对层次总排序作一致性检验。检验仍象层次总排序那样由高层到低层逐层进行。这是因为虽然各层次均已经过层次单排序的一致性检验,各成对比较判断矩阵都已具有较为满意的一致性。但当 综合考察时,各层次的非一致性仍有可能积累起来,引起最终分析结果较严重的非一致性。
设 B 层中与𝐴𝑗相关的因素的成对比较判断矩阵在单排序中经一致性检验,求得 单排序一致性
指标为 CI( j) ,( j = 1,…,m ),相应的平均随机一致性指标为 RI( j) (CI( j)、RI( j) 已在层次单
排序时求得),则 B 层总排序随机一致性比例为
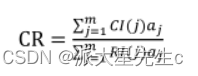
当 CR<0.1 时,认为层次总排序结果具有较满意的一致性并接受该分析结果。
④代码实现
matlab实现
disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>p
i=i+1;
x(:,i)=A*y(:,i-1);
m(i)=max(x(:,i));
y(:,i)=x(:,i)/m(i);
k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);disp(t);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
end
python代码如下:
import numpy as np
A = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]]) # 输入判断矩阵
(n, n) = np.shape(A)
# 算术平均法求权重
sum_1 = A.sum(axis=0) # 对每一列求和
B = A / sum_1 # 归一化处理
sum_2 = B.sum(axis=1) # 对每一行求和
suan = sum_2 / n # 除N得权重
print('算术平均法所得权重为:')
print(suan)
print('\n')
# 几何平均法求权重
multiply_1 = A.prod(axis=1) # 按行相乘
C = np.power(multiply_1, 1 / n) # 开n次方
sum_1 = C.sum(axis=0)
jihe = C / sum_1
print('几何平均法所得权重为:')
print(jihe)
print('\n')
# 特征值法求权重
D = np.linalg.eig(A)
max_eig = np.max(D[0]) # 最大特征值
position = np.argmax(D[0]) # 最大特征值位置
E = D[1] # 特征向量
E = E[:, position]
tezheng = E / sum(E) # 归一化处理
print('特征法所求权重为:')
print(tezheng)
print('\n')
# 计算一致性比例
CI = (max_eig - n) / (n - 1)
RI = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59]
CR = CI / RI[n - 1]
print('一致性指标CI:')
print(CI)
print('一致性比例CR:')
print(CR)
if CR < 0.1:
print('一致性可以接受')
else:
print('一致性不可接受')
⑤优缺点评价
优点:
(1)系统性:层次分析把研究对象作为一个系统,按照分解、比较判断、综合的思维方式进行决策,成为继机理分析、统计分析之后发展起来的系统分析的重要工具。
(2)实用性:层次分析把定性和定量方法结合起来,能处理许多许多用传统的最优化技术无法着手的实际问题,应用范围很广。同时,这种方法将决策者和决策分析者相互沟通,决策者甚至可以直接应用它,这就增加了决策者的了解和掌握。
(3)简洁性:具有中等文化程度的人即可了解层次分析的基本原理和掌握它的基本步骤,计算也非常简便,并且所得的结果简单明确,容易为决策者了解和掌握。
缺点:
囿旧:只能从原有方案中选优,不能生成新方案;
粗略:它的比较、判断直到结果都是粗糙的,不适于精度要求很高的问题;
主观:从建立层次结构模型到给出成对比较矩阵,人的主观因素的作用很大,这就使得决策结果可能难以为众人接受。可以采用主观和客观的方式求其权重的均值得到综合权重,在一定程度上相应的缩小了单一赋权法带来的局限性和弊端。
2、模糊综合评价法(FCE)
①应用场景
类似问卷调研,比较少用。适用于非线性问题。
②步骤
1、建立综合评价的因素集
2、建立综合评价的评价集
3、进行单因素模糊评价,获得评价矩阵
4、确定因素权向量
5、建立综合评定模型
③模型实现
1、这里设评定科研成果等级的指标集为 U=(u1,u2,u3,u4,u5) , u1 表示为科研成果发明或创造、革新的程度, u2 表示安全性能, u3 表示经济效益, u4 表示推广前景, u5 表示成熟性。
2、评价集是评价者对评价对象可能做出的各种结果所组成的集合,通常用V表示, V=(v1,v2,⋅⋅⋅,vn) ,其中元素 vj 代表第j种评价结果,可以根据实际情况的需要,用不同的等级、评语或数字来表示(注意下文中出现的m和n,m表示m个因素集,n 表示n 个评价集)。
这里设评定科研成果等级的评价集为 V=(v1,v2,v3,v4) , v1,v2,v3,v4 分别表示很好、较好、一般、不好(或者一等奖、二等奖、三等奖、四等奖,或者金牌、银牌、铜牌、铁牌)。
3、若因素集U中第i个元素对评价集V中第1个元素的隶属度为 ri1 ,则对第i个元素单因素评价的结果用模糊集合表示为: Ri=(ri1,ri2,⋅⋅⋅,rin) ,以m个单因素评价集 R1,R2,⋅⋅⋅,Rm 为行组成矩阵 Rm∗n ,称为模糊综合评价矩阵。
在实例中,某项科研成果通过专家评审打分,按下表给出U ×V 上每个有序对 (ui,vj) 指定的隶属度。
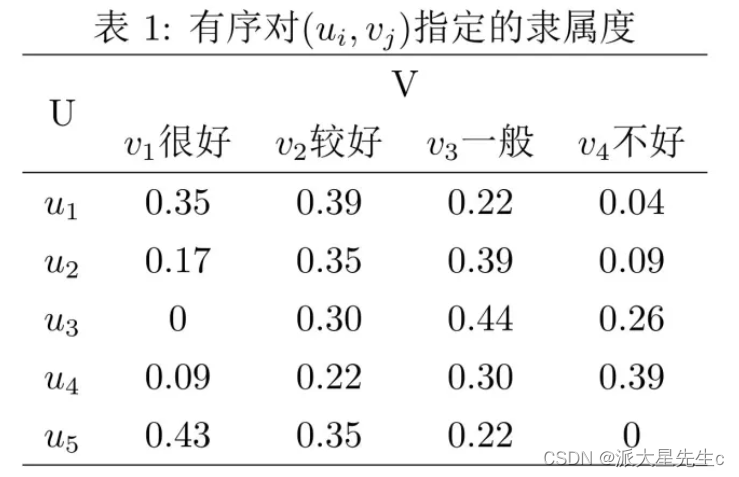
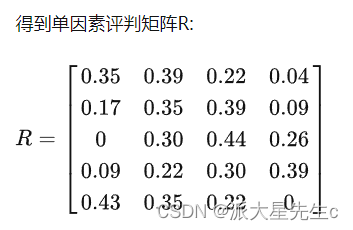
4、评价工作中,各因素的重要程度有所不同,为此,给各因素 ui 一个权重 ai ,各因素的权重集合的模糊集,用A表示: A=(a1,a2,⋅⋅⋅,am) 。
在实例中,为了评定作者的学术成就,取权数分配 A=(0.35,0.35,0.1,0.1,0.1) 。(这里给出的权向量较为简便,其实可以通过层次分析法AHP的成对比较阵来构造这个权向量。)
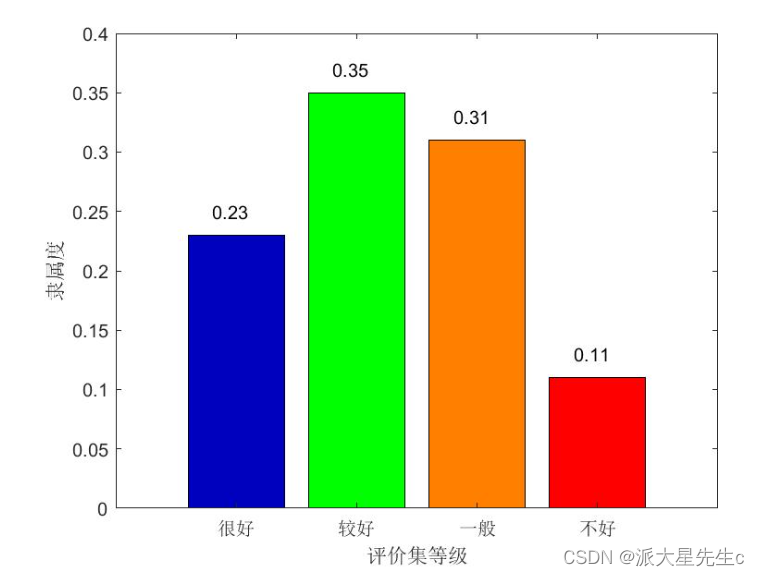
5、确定单因素评判矩阵R和因素权向量A之后,通过模糊变化将U上的模糊向量A变为V上的模糊向量B,即 B=A1∗m∘Rm∗n=(b1,b2,⋅⋅⋅,bn) 。 其中 ∘ 称为综合评价合成算子,这里取成一般的矩阵乘法即可。
在实例中,最后得到的模糊向量为 B=A∗R=(0.23,0.35,0.31,0.11) ,由计算结果可见,该成果应被评为二等奖。
6、综合评价模型确定后,确定系统得分,即 F=B1∗n∗S1∗nT ,其中F为系统总得分,S 为V 中相应因素的级分。在实例中,一等奖的级分肯定最高,其次是二等奖,依次往下,设级分依次为 S=(100,80,60,30) ,则该成果最后的系统总得分为72.9。
如果是多目标的模糊综合评价,对于同一批专家打分,最后的系统总得分就相对来说较为可信,从本例来看,就可以对各个成果相互比较最后的综合得分。
参考文章:数模系列(3):模糊综合评价法 - 知乎 (zhihu.com)

3、灰色关联分析法(GRA)
①应用场景
灰色关联分析的基本思想 是根据序列曲线几何形状的相似程度来判断其联系是否紧密,曲线越接近,相应序列之间的关联度就越大,反之则越小。
此方法可用于 进行系统分析,也可应用于对问题 进行综合评价。
②步骤
1、确定分析数列
母序列(又称参考数列,母指标):能反映系统行为特征的数据序列——>类似与因变量Y
子序列(又称比较数列,子指标):影响系统行为的因素组成的数据序列——>类似与自变量X
2、对变量进行预处理(去量纲,缩小变量范围,简化计算),先求出每个指标列的均值,再用该指标列的每一个元素都除以该指标列的均值
3、用子序列中每一个元素减去对应母序列中同一行的那个元素,并取绝对值,由此得到一个新矩阵new_X。
4、记a为矩阵中的最小元素,b为矩阵中的最大元素,分辨系数ro通常为0.5,那么每一个元素对应母序列的关联系数为 a+rob./(new_X+rob)
5、然后,我们再对得到的关联系数矩阵求每一列均值,得到的最后结果gamma就是每一个指标对于母序列的灰色关联度
③模型实现
应用一:分析产业对GDP的影响程度
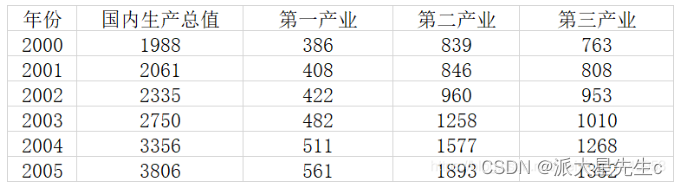
%% 应用一:分析产业对GDP的影响程度
clear;clc;
load data.mat;
r = size(data,1);
c = size(data,2);
%第一步,对变量进行预处理,消除量纲的影响(大家在使用时需要注意自己的数据量纲是否相同)
%avg = repmat(mean(data),r,1);
%data = data./avg;
%定义母序列和子序列
Y = data(:,1); %母序列
X = data(:,2:c); %子序列
Y2 = repmat(Y,1,c-1); %把母序列向右复制到c-1列
absXi_Y = abs(X-Y2)
a = min(min(absXi_Y)) %全局最小值
b = max(max(absXi_Y)) %全局最大值
ro = 0.5; %分辨系数取0.5
gamma = (a+ro*b)./(absXi_Y+ro*b) %计算子序列中各个指标与母序列的关联系数
disp("子序列中各个指标的灰色关联度分别为:");
ans = mean(gamma)
子序列中各个指标的灰色关联度分别为:
ans =
0.7319 0.8983 0.8518
应用二:灰色关联分析评价河流情况
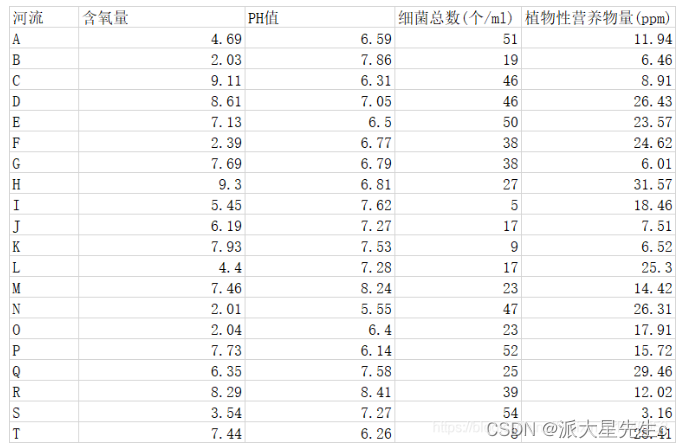
%应用二:灰色关联分析评价河流情况
clear;clc;
load X.mat;
%获取行数列数
r = size(X,1);
c = size(X,2);
%首先,把我们的原始指标矩阵正向化
%第二列中间型--->极大型
middle = input("请输入最佳的中间值:");
M = max(abs(X(:,2)-middle));
for i=1:r
X(i,2) = 1-abs(X(i,2)-middle)/M;
end
%第三列极小型--->极大型
max_value = max(X(:,3));
X(:,3) = abs(X(:,3)-max_value);
%第四列区间型--->极大型
a = input("请输入区间的下界:");
b = input("请输入区间的下界:");
M = max(a-min(X(:,4)),max(X(:,4))-b);
for i=1:r
if (X(i,4)<a)
X(i,4) = 1-(a-X(i,4))/M;
elseif (X(i,4)<=b&&X(i,4)>=a)
X(i,4) = 1;
else
X(i,4) = 1-(X(i,4)-b)/M;
end
end
disp("正向化后的矩阵为:");
disp(X);
%把正向化后的矩阵进行预处理,消除量纲的影响
avg = repmat(mean(X),r,1);
new_X = X./avg;
%将预处理后的矩阵每一行的最大值取出,当成母序列(虚构的)
Y = max(new_X,[],2);
%计算各个指标和母序列的灰色关联度
%先把new_X矩阵所有元素都减去母序列中同行的元素,并取绝对值
Y2 = repmat(Y,1,c);
new_X = abs(new_X-Y2);
a = min(min(new_X)); %全矩阵最小值
b = max(max(new_X)); %全矩阵最大值
ro = 0.5;
new_X = (a+ro*b)./(new_X+ro*b);
disp("各个指标对于母序列的灰色关联度为:");
gamma = mean(new_X)
%计算各个指标的权重
disp("各个指标的权重为:");
weight = gamma./(sum(gamma,2))
%-------------------------------------------------------------------------------------------------------
%继续TOPSIS的步骤:对正向化后的矩阵X进行标准化(原矩阵除以每一列元素平方之和的开方)
temp1 = X.*X; %先让每每一个元素平方
temp2 = sum(temp1); %再对每一列求和
temp3 = temp2.^0.5; %再把结果开方
temp4 = repmat(temp3,r,1); %把开方后的结果按行复制r行
disp("******标准化后的矩阵为:");
Z = X./temp4 %原矩阵除以每一列元素平方之和的开方
Z_max = max(Z) %获得Z每一列中最大的元素
Z_min = min(Z) %获得Z每一列中最小的元素
D_max = sum(weight.*(Z-repmat(Z_max,r,1)).^2,2).^0.5
D_min = sum(weight.*(Z-repmat(Z_min,r,1)).^2,2).^0.5
disp("该矩阵得分为:")
S = D_min./(D_max+D_min)
disp("矩阵归一化后得分为:");
S = S./(repmat(sum(S),r,1))
输出结果为:
请输入最佳的中间值:7
请输入区间的下界:10
请输入区间的上界:20
正向化后的矩阵为:
4.6900 0.7172 3.0000 1.0000
2.0300 0.4069 35.0000 0.6940
9.1100 0.5241 8.0000 0.9058
8.6100 0.9655 8.0000 0.4443
7.1300 0.6552 4.0000 0.6914
2.3900 0.8414 16.0000 0.6007
7.6900 0.8552 16.0000 0.6551
9.3000 0.8690 27.0000 0
5.4500 0.5724 49.0000 1.0000
6.1900 0.8138 37.0000 0.7848
7.9300 0.6345 45.0000 0.6992
4.4000 0.8069 37.0000 0.5419
7.4600 0.1448 31.0000 1.0000
2.0100 0 7.0000 0.4546
2.0400 0.5862 31.0000 1.0000
7.7300 0.4069 2.0000 1.0000
6.3500 0.6000 29.0000 0.1824
8.2900 0.0276 15.0000 1.0000
3.5400 0.8138 0 0.4088
7.4400 0.4897 46.0000 0.2731
new_X =
0.7831 1.2228 0.1345 1.4997
0.3390 0.6937 1.5695 1.0408
1.5211 0.8936 0.3587 1.3584
1.4376 1.6461 0.3587 0.6662
1.1905 1.1170 0.1794 1.0369
0.3991 1.4345 0.7175 0.9008
1.2840 1.4580 0.7175 0.9825
1.5528 1.4815 1.2108 0
0.9100 0.9759 2.1973 1.4997
1.0336 1.3874 1.6592 1.1769
1.3241 1.0817 2.0179 1.0486
0.7347 1.3757 1.6592 0.8127
1.2456 0.2469 1.3901 1.4997
0.3356 0 0.3139 0.6818
0.3406 0.9994 1.3901 1.4997
1.2907 0.6937 0.0897 1.4997
1.0603 1.0229 1.3004 0.2735
1.3842 0.0470 0.6726 1.4997
0.5911 1.3874 0 0.6131
1.2423 0.8348 2.0628 0.4096
Y2 =
1.4997 1.4997 1.4997 1.4997
1.5695 1.5695 1.5695 1.5695
1.5211 1.5211 1.5211 1.5211
1.6461 1.6461 1.6461 1.6461
1.1905 1.1905 1.1905 1.1905
1.4345 1.4345 1.4345 1.4345
1.4580 1.4580 1.4580 1.4580
1.5528 1.5528 1.5528 1.5528
2.1973 2.1973 2.1973 2.1973
1.6592 1.6592 1.6592 1.6592
2.0179 2.0179 2.0179 2.0179
1.6592 1.6592 1.6592 1.6592
1.4997 1.4997 1.4997 1.4997
0.6818 0.6818 0.6818 0.6818
1.4997 1.4997 1.4997 1.4997
1.4997 1.4997 1.4997 1.4997
1.3004 1.3004 1.3004 1.3004
1.4997 1.4997 1.4997 1.4997
1.3874 1.3874 1.3874 1.3874
2.0628 2.0628 2.0628 2.0628
new_X =
0.7166 0.2769 1.3651 0
1.2306 0.8758 0 0.5287
0 0.6275 1.1624 0.1627
0.2085 0 1.2873 0.9799
0 0.0735 1.0111 0.1536
1.0354 0 0.7170 0.5336
0.1739 0 0.7405 0.4755
0 0.0714 0.3421 1.5528
1.2873 1.2214 0 0.6976
0.6256 0.2718 0 0.4823
0.6938 0.9362 0 0.9693
0.9245 0.2835 0 0.8465
0.2541 1.2528 0.1095 0
0.3462 0.6818 0.3679 0
1.1591 0.5003 0.1095 0
0.2090 0.8060 1.4100 0
0.2402 0.2775 0 1.0270
0.1155 1.4526 0.8270 0
0.7963 0 1.3874 0.7743
0.8205 1.2280 0 1.6532
各个指标对于母序列的灰色关联度为:
gamma =
0.6665 0.6800 0.7052 0.6880
各个指标的权重为:
weight =
0.2433 0.2482 0.2574 0.2511
******标准化后的矩阵为:
Z =
0.1622 0.2483 0.0245 0.3065
0.0702 0.1408 0.2863 0.2127
0.3150 0.1814 0.0655 0.2776
0.2977 0.3342 0.0655 0.1361
0.2466 0.2268 0.0327 0.2119
0.0826 0.2912 0.1309 0.1841
0.2659 0.2960 0.1309 0.2008
0.3216 0.3008 0.2209 0
0.1885 0.1981 0.4009 0.3065
0.2141 0.2817 0.3027 0.2405
0.2742 0.2196 0.3682 0.2143
0.1522 0.2793 0.3027 0.1661
0.2580 0.0501 0.2536 0.3065
0.0695 0 0.0573 0.1393
0.0705 0.2029 0.2536 0.3065
0.2673 0.1408 0.0164 0.3065
0.2196 0.2077 0.2373 0.0559
0.2867 0.0095 0.1227 0.3065
0.1224 0.2817 0 0.1253
0.2573 0.1695 0.3763 0.0837
Z_max =
0.3216 0.3342 0.4009 0.3065
Z_min =
0.0695 0 0 0
D_max =
0.2109
0.1739
0.1870
0.1907
0.2034
0.1920
0.1506
0.1794
0.0944
0.0841
0.0788
0.1231
0.1631
0.2839
0.1587
0.2192
0.1708
0.2153
0.2448
0.1427
D_min =
0.2028
0.1934
0.2081
0.2148
0.1787
0.1844
0.2137
0.2247
0.2795
0.2508
0.2619
0.2270
0.2223
0.0756
0.2244
0.1952
0.1774
0.1974
0.1559
0.2322
该矩阵得分为:
S =
0.4902
0.5265
0.5266
0.5297
0.4677
0.4899
0.5866
0.5559
0.7476
0.7489
0.7686
0.6483
0.5768
0.2104
0.5857
0.4710
0.5095
0.4782
0.3891
0.6194
矩阵归一化后得分为:
S =
0.0449
0.0482
0.0482
0.0485
0.0428
0.0448
0.0537
0.0509
0.0684
0.0685
0.0703
0.0593
0.0528
0.0193
0.0536
0.0431
0.0466
0.0438
0.0356
0.0567
二、客观评价
1、主成分分析(PCA)
可以参考我之前总结的文章《数学建模--数据预处理》
主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
2、因子分析(FA)
①应用场景
减少分析变量个数
通过对变量间相关关系的探测,将原始变量分组,即将相关性高的变量分为一组,用共性因子来代替该变量
使问题背后的业务因素的意义更加清晰呈现
②步骤
1、选择分析的变量
2、计算所选原始变量的相关系数矩阵
3、提取公共因子
4、因子旋转
5、计算因子得分
③模型分析
以废气排放为例说明主成分降维处理过程
1、评价标准体系的构建
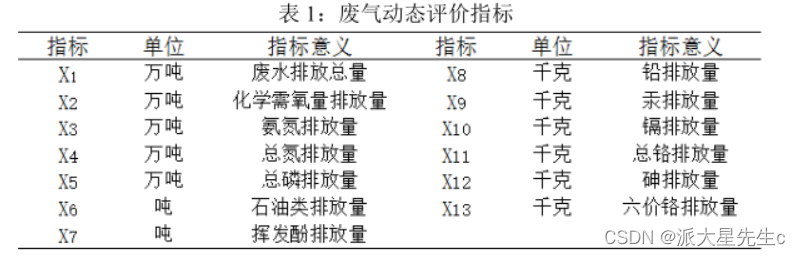
2、因子分析
因子分析首先将原始数据标准化处理,建立相关系数矩 阵并计算其特征值和特征向量,接着从中选择特征值大于等 于1的特征值个数为公共因子数,或者根据因子对X的累计贡献 率大于80%来确定公共因子,求得因子载荷矩阵, 后计算公因子得分和综合得分。
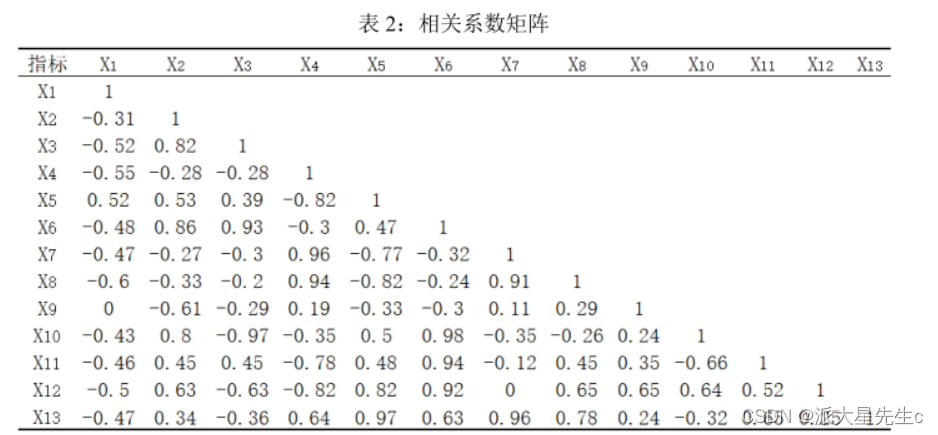
观察相关系数矩阵表 2,可以发现所选取指标之间存在着一定的相关关系,其中 X3 和 X6、X4 和
X7、 X7 和 X8 分别存在着较强的相关性,相关系数分别为 0.96、 0.96、0.91,这进一步验证了对所选指标做因子分析的科学性和必要性。计算相关系数矩阵的特征值、贡献率及累计贡献率如
所示:
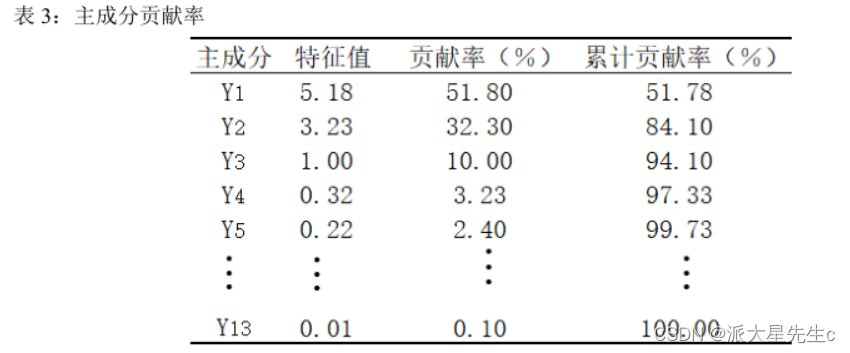
确定提取的主成分个数可综合考虑 3 个方面:
(1)提取的所有特征值大于某一特定特征值,一般特定值设为 1,本文同样以 1 为标准;
(2) 提取的主成分的累计贡献率要大于 85%,即所提取的主成分要能够概括原有指标的绝大部分信息; 由表 3 可知,前 3 个主成分的累计贡献率已经达到了94.01%,满足按照累计贡献率大于 85% 确定主成分个数的原则;
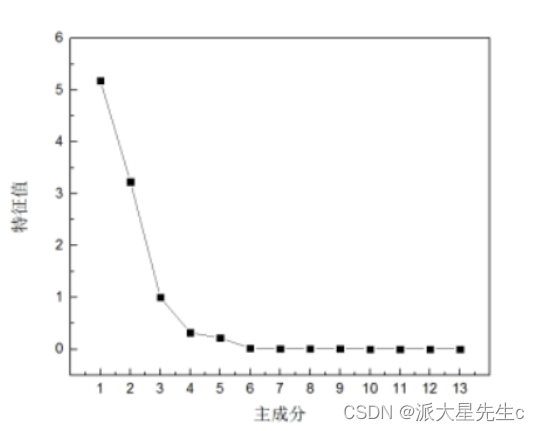
(3) 以做主成分分析时生成的碎石图 (Scree Plot) 做参考,碎石图是按照特征值大小排列的,以特征值为纵坐标、因子数为横坐标生成的主成分散点图,有明显的拐点,一般取拐点前所有的因子及拐点后第一个因子作为主成分 。
观察图 4 可得,第一、第二个主成分的特征值较大,其余几个均较小,碎石图在第三个特征值出现
拐点。
根据上述分析,在本研究中选取前 3 个主成分对河南省水资源使用情况进行动态分析,从表 3
和 4,我们可以看出前 3 个主成分已经能够概括绝大部分的原始信息,因此提取 3 个主成分因子是
合理的. 提取 3 个主成分用于概括原有 10 个指标的绝大部分信息,这既达到了降维、简化的目的,又在一定程度上保证了后续研究结果能准确有效地反映出河南省水资源使用情况动态变化的基本特征。计算主成分的载荷矩阵, 主成分载荷是指提取的 3 大主成分与各变量指标之间的相关系数如表4:

④代码实现
clc,clear
r=[1.000 0.577 0.509 0.387 0.462
0.577 1.000 0.599 0.389 0.322
0.509 0.599 1.000 0.436 0.426
0.387 0.389 0.436 1.000 0.523
0.462 0.322 0.426 0.523 1.000];
%下面利用相关系数矩阵求主成分解,val的列为r的特征向量,即主成分的系数
[vec,val,con]=pcacov(r);%val为r的特征值,con为各个主成分的贡献率
f1=repmat(sign(sum(vec)),size(vec,1),1); %构造与vec同维数的元素为±1的矩阵
vec=vec.*f1; %修改特征向量的正负号,每个特征向量乘以所有分量和的符号函数值
f2=repmat(sqrt(val)',size(vec,1),1);
a=vec.*f2 %构造全部因子的载荷矩阵
a1=a(:,1) %提出一个因子的载荷矩阵
tcha1=diag(r-a1*a1') %计算一个因子的特殊方差
a2=a(:,[1,2]) %提出两个因子的载荷矩阵
tcha2=diag(r-a2*a2') %计算两个因子的特殊方差
ccha2=r-a2*a2'-diag(tcha2) %求两个因子时的残差矩阵
gong=cumsum(con) %求累积贡献率
clc,clear
load data.txt; %把原始数据保存在纯文本文件data.txt中
n=size(data,1);
x=data(:,1:4); y=data(:,5); %分别提出自变量x和因变量y的值
——————————————————————————————————
如果不需要检验,则不需要把y列入原始数据中,把矩阵x的大小改变一下,以及下文中的m,m为原始数据中变量的个数。
——————————————————————————————————
m=4;%m为变量的个数
x=zscore(x); %数据标准化
r=cov(x); %求标准化数据的协方差阵,即求相关系数矩阵
[vec,val,con]=pcacov(r); %进行主成分分析的相关计算
c=cumsum(con);
i=1;
while ((c(i)<90)&(con(i+1)>10))
i=i+1;
end
num=i;
f1=repmat(sign(sum(vec)),size(vec,1),1);
vec=vec.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec,1),1);
a=vec.*f2; %求初等载荷矩阵
am=a(:,1:num); %提出num个主因子的载荷矩阵
[b,t]=rotatefactors(am,'method', 'varimax'); %旋转变换,b为旋转后的载荷阵
bt=[b,a(:,num+1:end)]; %旋转后全部因子的载荷矩阵
contr=sum(bt.^2); %计算因子贡献
rate=contr(1:num)/sum(contr); %计算因子贡献率
fprintf('综合因子得分公式:F=');
for i=1:num
fprintf('+%f*F%d',rate(i),i);
end
fprintf('\n');
coef=inv(r)*b; %计算得分函数的系数
coef=coef';
for i=1:num
fprintf('各个因子得分函数为F%d=',i);
for j=1:m
fprintf('+(%f)*x_%d',coef(i,j),j);
end
fprintf('\n');
end
%如果仅仅因子分析,程序到此为止
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
score=x*coef';%计算各个因子的得分
weight=rate/sum(rate); %计算得分的权重
Tscore=score*weight'; %对各因子的得分进行加权求和,即求各企业综合得分
[STscore,ind]=sort(Tscore,'descend'); %对企业进行排序
display=[score(ind,:)';STscore';ind']; %显示排序结果
fprintf('排序结果如下:');
for i=1:num
fprintf('第%d行为F%d得分,',i,i);
end
fprintf('第%d行为综合因子得分,第%d为原序列\n',num+1,num+2);
disp(display);
[ccoef,p]=corrcoef([Tscore,y]); %计算F与资产负债的相关系数
[d,dt,e,et,stats]=regress(Tscore,[ones(n,1),y]);%计算F与资产负债的方程
fprintf('因子分析法的回归方程为:F=%f+(%f*y)',d(1),d(2));
if (stats(3)<0.05)%判断是否通过显著性检验的结果
fprintf('\n在显著性水平0.05的情况下,通过了假设检验。\n');
else
fprintf('\n在显著性水平0.05的情况下,通不过假设检验。\n');
end该MATLAB源代码的displsy为最终排序结果。
3、Topsis算法
Topsis算法基本思想:基于归一化后的原始数据矩阵,采用余弦法找出有限方案中的最优方案和最劣方案(分别用最优向量和最劣向量表示),然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。
①应用场景
多目标决策分析
②步骤

1、计算规范化矩阵

2、构造权重规范化矩阵

3、确定理想解和反理想解

4、计算距离尺度

5、计算理想解的贴近度

6、根据理想解的贴近度进行排序

③模型分析
例:小明同宿舍共有四名同学,他们第一学期的成绩、以及与他们吵架的次数(两种因素)如下表所示,请你为这四名同学进行评分,该评分能合理的描述综合成绩的高低。
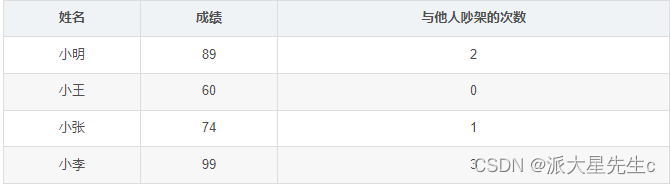
标准化过后
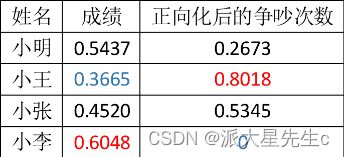
最大值:[0.6048, 0.8018],最小值:[0.3665, 0]

未归一化的得分:

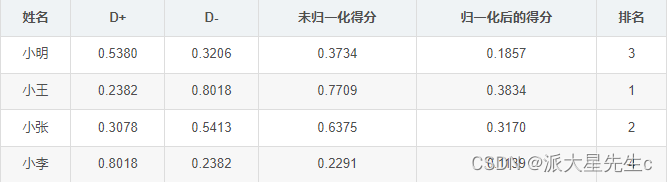
- 将原始矩阵正向化。(为了统一指标,方便后面计算,因此将指标统一为极大型指标)
- 将正向话矩阵标准化。(消除量纲的影响)
- 计算得分并归一化。(统计各指标的最大值,与最小值,并计算得分)
④代码实现
%自定义函数 Positivization.m
function [posit_x] = Positivization(x,type,i)
% 输入变量有三个:
% x:需要正向化处理的指标对应的原始列向量
% type: 指标的类型(1:极小型, 2:中间型, 3:区间型)
% i: 正在处理的是原始矩阵中的哪一列
% 输出变量posit_x表示:正向化后的列向量
if type == 1 %极小型
disp(['第' num2str(i) '列是极小型,正在正向化'] )
posit_x = Min2Max(x); %调用Min2Max函数来正向化
disp(['第' num2str(i) '列极小型正向化处理完成'] )
disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
elseif type == 2 %中间型
disp(['第' num2str(i) '列是中间型'] )
best = input('请输入最佳的那一个值: ');
posit_x = Mid2Max(x,best);
disp(['第' num2str(i) '列中间型正向化处理完成'] )
disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
elseif type == 3 %区间型
disp(['第' num2str(i) '列是区间型'] )
a = input('请输入区间的下界: ');
b = input('请输入区间的上界: ');
posit_x = Inter2Max(x,a,b);
disp(['第' num2str(i) '列区间型正向化处理完成'] )
disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
else
disp('没有这种类型的指标,请检查Type向量中是否有除了1、2、3之外的其他值')
end
end
%% 第一步:把数据复制到工作区,并将这个矩阵命名为X
% (1)在工作区右键,点击新建(Ctrl+N),输入变量名称为X
% (2)在Excel中复制数据,再回到Excel中右键,点击粘贴Excel数据(Ctrl+Shift+V)
% (3)关掉这个窗口,点击X变量,右键另存为,保存为mat文件(下次就不用复制粘贴了,只需使用load命令即可加载数据)
% (4)注意,代码和数据要放在同一个目录下哦,且Matlab的当前文件夹也要是这个目录。
clear;clc
load data_water_quality.mat
%% 第二步:判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标'])
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理,需要请输入1 ,不需要输入0: ']);
if Judge == 1
Position = input('请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]: '); %[2,3,4]
disp('请输入需要处理的这些列的指标类型(1:极小型, 2:中间型, 3:区间型) ')
Type = input('例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]: '); %[2,1,3]
% 注意,Position和Type是两个同维度的行向量
for i = 1 : size(Position,2) %这里需要对这些列分别处理,因此我们需要知道一共要处理的次数,即循环的次数
X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
% Positivization是我们自己定义的函数,其作用是进行正向化,其一共接收三个参数
% 第一个参数是要正向化处理的那一列向量 X(:,Position(i)) 回顾上一讲的知识,X(:,n)表示取第n列的全部元素
% 第二个参数是对应的这一列的指标类型(1:极小型, 2:中间型, 3:区间型)
% 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
% 该函数有一个返回值,它返回正向化之后的指标,我们可以将其直接赋值给我们原始要处理的那一列向量
end
disp('正向化后的矩阵 X = ')
disp(X)
end
%% 在这里增加是否需要算加权
% % 假如原始数据为:
% A=[1, 2, 3;
% 2, 4, 6]
% % 权重矩阵为:
% B=[ 0.2, 0.5 ,0.3 ]
% % 加权后为:
% C=A .* B
% 0.2000 1.0000 0.9000
% 0.4000 2.0000 1.8000
% 类似的,还有矩阵和向量的点除, 大家可以自己试试计算A ./ B
% 注意,矩阵和向量没有 .- 和 .+ 哦 ,大家可以试试,如果计算A.+B 和 A.-B会报什么错误。
%% 让用户判断是否需要增加权重
disp("请输入是否需要增加权重向量,需要输入1,不需要输入0")
Judge = input('请输入是否需要增加权重: ');
if Judge == 1
disp(['如果你有3个指标,你就需要输入3个权重,例如它们分别为0.25,0.25,0.5, 则你需要输入[0.25,0.25,0.5]']);
weigh = input(['你需要输入' num2str(m) '个权数。' '请以行向量的形式输入这' num2str(m) '个权重: ']);
OK = 0; % 用来判断用户的输入格式是否正确
while OK == 0
if abs(sum(weigh) - 1)<0.000001 && size(weigh,1) == 1 && size(weigh,2) == m % 这里要注意浮点数的运算是不精准的。
OK =1;
else
weigh = input('你输入的有误,请重新输入权重行向量: ');
end
end
else
weigh = ones(1,m) ./ m ; %如果不需要加权重就默认权重都相同,即都为1/m
end
%% 第三步:对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)
%% 第四步:计算与最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5; % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5; % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N); % 未归一化的得分
disp('最后的得分为:')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')
4、BP神经网络综合评价法
基本思想:
是一种交互式的评价方法,它可以根据用户期望的输出不断修改指标的权值,直到用户满意为止。因此,一般来说,人工神经网络评价方法得到的结果会更符合实际情况。
①应用场景
神经网络评价模型具有自适应能力、可容错性,能够处理非线性、非局域性的大型复杂系统。在对学习样本训练中,无需考虑输入因子之间的权系数,ANN通过输入值与期望值之间的误差比较,沿原连接权自动地进行调节和适应,因此该方法体现了因子之间的相互作用。
②优缺点分析
优点:
神经网络具有自适应能力,能对多指标综合评价问题给出一个客观评价,这对于弱化权重确定中的人为因素是十分有益的。在以前的评价方法中,传统的权重设计带有很大的模糊性,同时权重确定中人为因素影响也很大。随着时间、空间的推移,各指标对其对应题的影响程度也可能发生变化,确定的初始权重不一定符合实际情况。再者,考虑到整个分析评价是一个复杂的非线性大系统,必须建立权重的学习机制,这些方面正是人工神经网络的优势所在。针对综合评价建模过程中变量选取方法的局限性,采用神经网络原理可对变量进行贡献分析,进而剔除影响不显著和不重要的因素,以建立简化模型,可以避免主观因素对变量选取的干扰。
缺点:
ANN在应用中遇到的最大问题是不能提供解析表达式,权值不能解释为一种回归系数,也不能用来分析因果关系,目前还不能从理论上或从实际出发来解释ANN的权值的意义。需要大量的训练样本,精度不高,应用范围是有限的。最大的应用障碍是评价算法的复杂性,人们只能借助计算机进行处理,而这方面的商品化软件还不够成熟。
原文链接:https://blog.csdn.net/weixin_42616102/article/details/81008100
③代码实现
p1=data(1:7776,1:3);
th1=data(1:7776,4:4);
tfe1=data(1:7776,5:5);
p2=data(7777:8640,1:3);
th2=data(7777:8640,4:4);
tfe2=data(7777:8640,5:5);
p1=p1';%输入变量矩阵 3*7776
th1=th1';%输出矩阵 1*7776
tfe1=tfe1';
p2=p2';%测试样本输入变量矩阵 3*864
th2=th2';%测试样本输出矩阵 1*864
tfe2=tfe2';
%对数据进行归一化处理
%训练样本归一化
[ph,minp,maxp,th,minth,maxth]=premnmx(p1,th1);
[pfe,minpfe,maxpfe,tfe,mintfe,maxtfe]=premnmx(p1,tfe1);
%测试样本归一化
[ph_test,minph_test,maxph_test,th_test,minth_test,maxth_test]=premnmx(p2,th2);
[pfe_test,minpfe_test,maxpfe_test,tfe_test,mintfe_test,maxtfe_test]=premnmx(p2,tfe2);
%创建网络 三个输入神经元,两个输出神经元 Nodenum为隐含层神经元个数取值(2—15)
Nodenum=5;
neth=newff(minmax(ph),[Nodenum,1],{'tansig','purelin'},'traingdm');
netfe=newff(minmax(pfe),[Nodenum,1],{'tansig','purelin'},'traingdm');
%训练网络
net.trainParam.show=100;%每训练100次刷新一次训练误差图
net.trainParam.Ir=0.05;%学习率
net.trainParam.mc=0.9;%动量因子设定
net.trainParam.epochs=1000;%训练次数
net.trainParam.gold=0.0001;%训练结束的目标
%调用traingdm算法训练BP网络
neth=train(neth,ph,th);
netfe=train(netfe,pfe,tfe);
%训练仿真
yh1=sim(neth,ph);
yfe1=sim(netfe,pfe);
%反归一化
h1=postmnmx(yh1,minth,maxth);
pause
fe1=postmnmx(yfe1,mintfe,maxtfe);
pause
%性能分析
%误差
Eh=h1-th1;%误差
MEh(1)=max(abs(Eh));%误差最大值
MEh(2)=min(abs(Eh));%误差最小值
MEh(3)=mean(abs(Eh));%误差平均值
MEh(4)=std(Eh);%误差方差
MEh(5)=MEh(3)/mean(th1);%平均误差率
MEh(6)=mse(Eh);
pause
Efe=fe1-tfe1;
MEfe(1)=max(abs(Efe));
MEfe(2)=min(abs(Efe));
MEfe(3)=mean(abs(Efe));
MEfe(4)=std(Efe);
MEfe(5)=MEfe(3)/mean(tfe1);
MEfe(6)=mse(Efe);
pause
%测试
%测试仿真
yh_test=sim(neth,ph_test);
pause
yfe_test=sim(netfe,pfe_test);
pause
%反归一化
h_test=postmnmx(yh_test,minth,maxth);
fe_test=postmnmx(yfe_test,mintfe,maxtfe);
%性能分析
%均方误差
%误差
Eh_test=h_test-th2;
MEh_test(1)=max(abs(Eh_test));%误差最大值
MEh_test(2)=min(abs(Eh_test));%误差最小值
MEh_test(3)=mean(abs(Eh_test));%误差平均值
MEh_test(4)=std(Eh_test);%误差方差
MEh_test(5)=MEh(3)/mean(th2);%平均误差率
MEh_test(6)=mse(Eh_test);
pause
Efe_test=fe_test-tfe2;
MEfe_test(1)=max(abs(Efe_test));
MEfe_test(2)=min(abs(Efe_test));
MEfe_test(3)=mean(abs(Efe_test));
MEfe_test(4)=std(Efe_test);
MEfe_test(5)=MEfe(3)/mean(tfe2);
MEfe_test(6)=mse(Efe_test);
pause
M=[MEh;MEfe;MEh_test;MEfe_test]
版权归原作者 派大星先生c 所有, 如有侵权,请联系我们删除。
