李永乐老师讲解
讲解视频
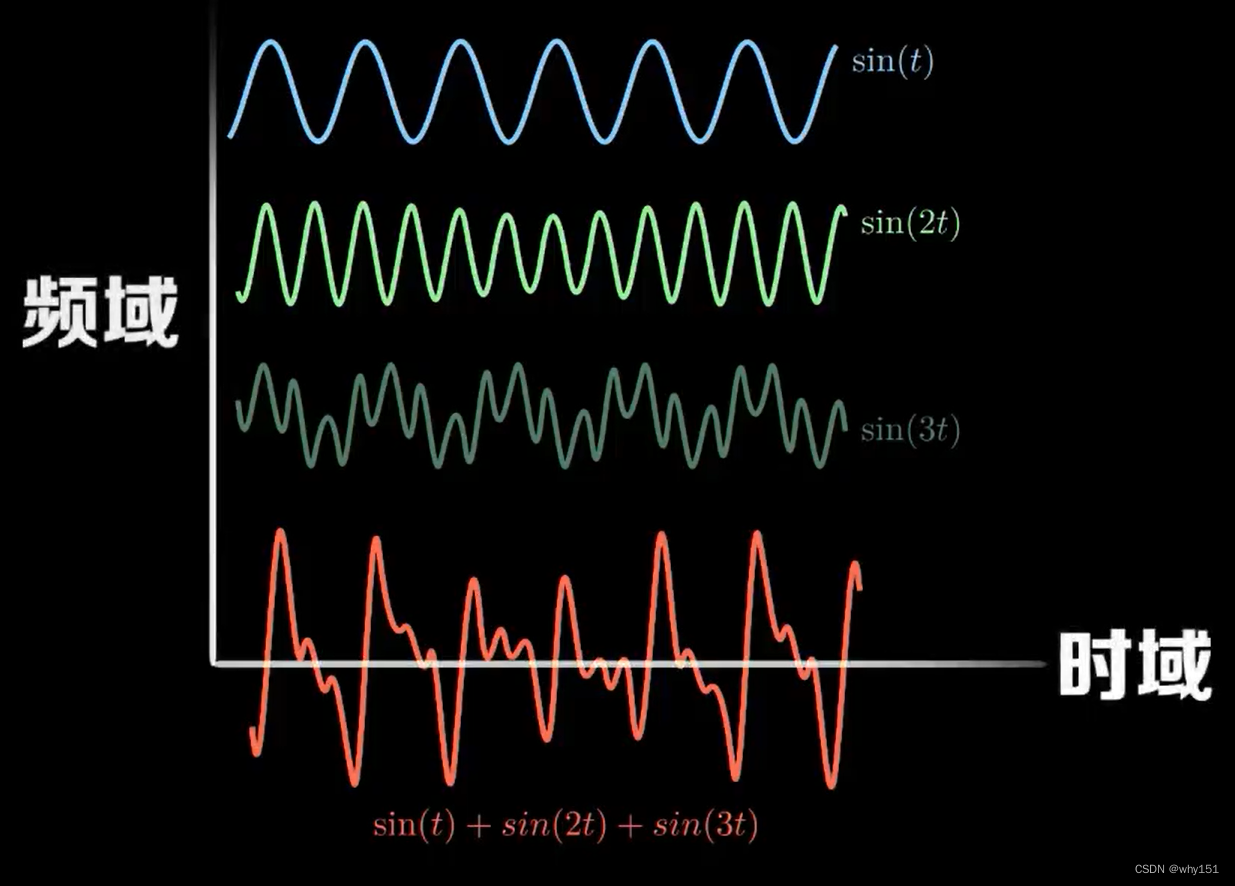
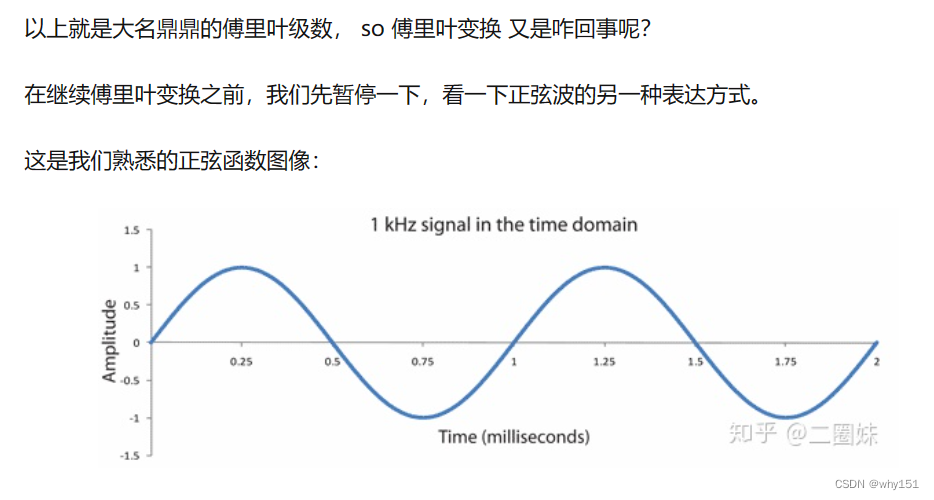
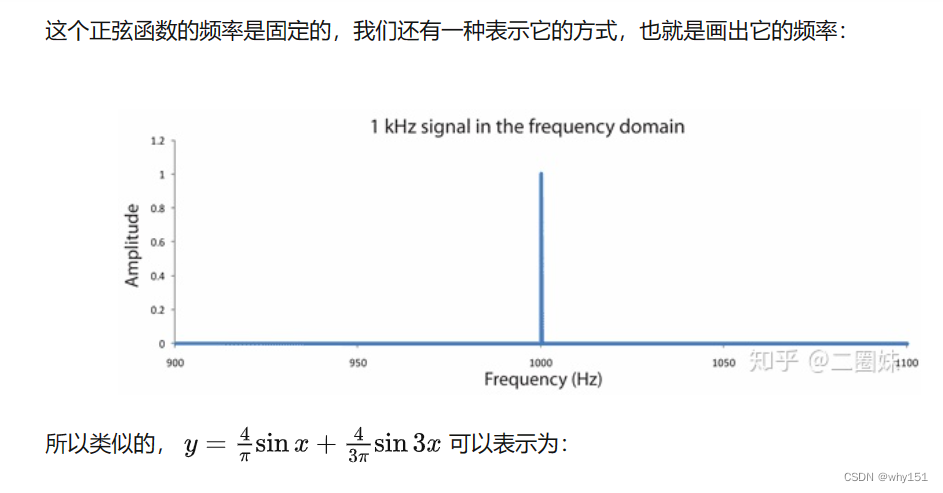
振幅、频率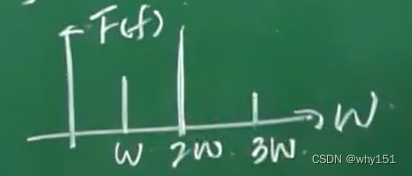
相位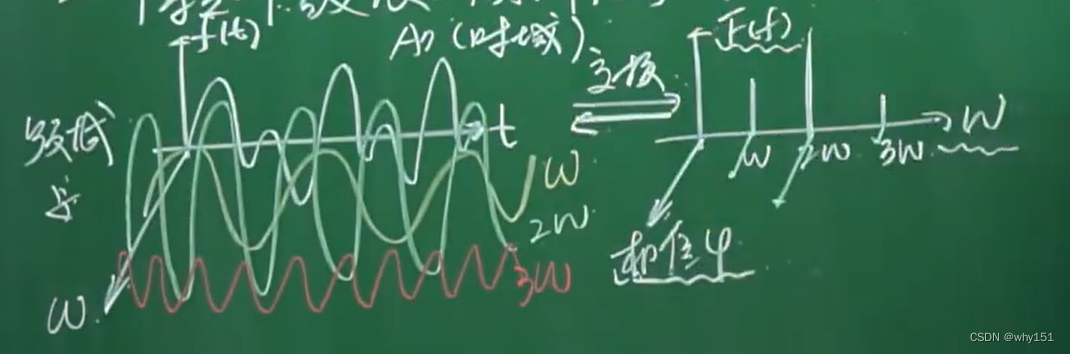
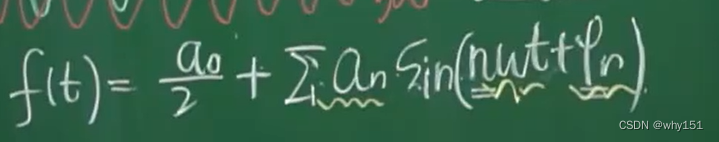
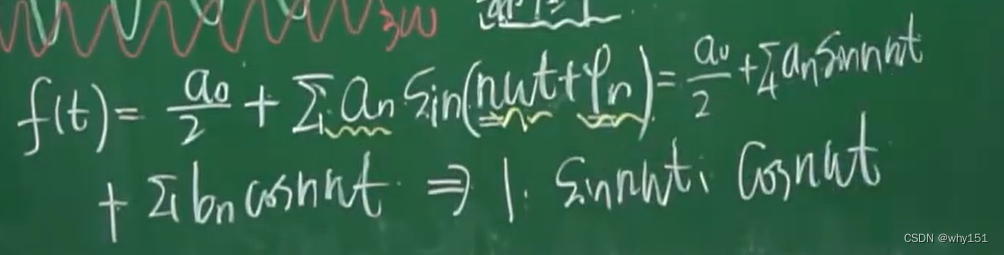

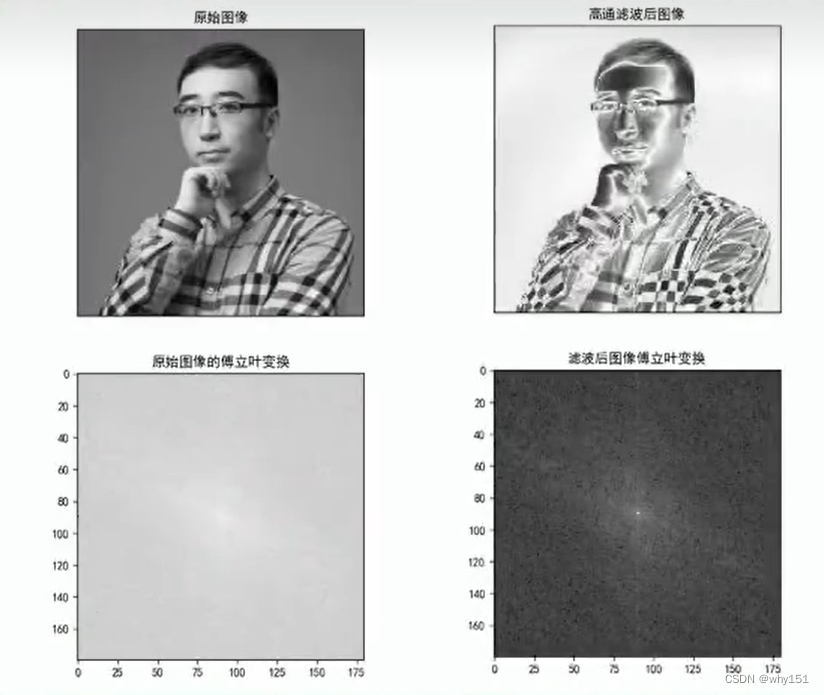
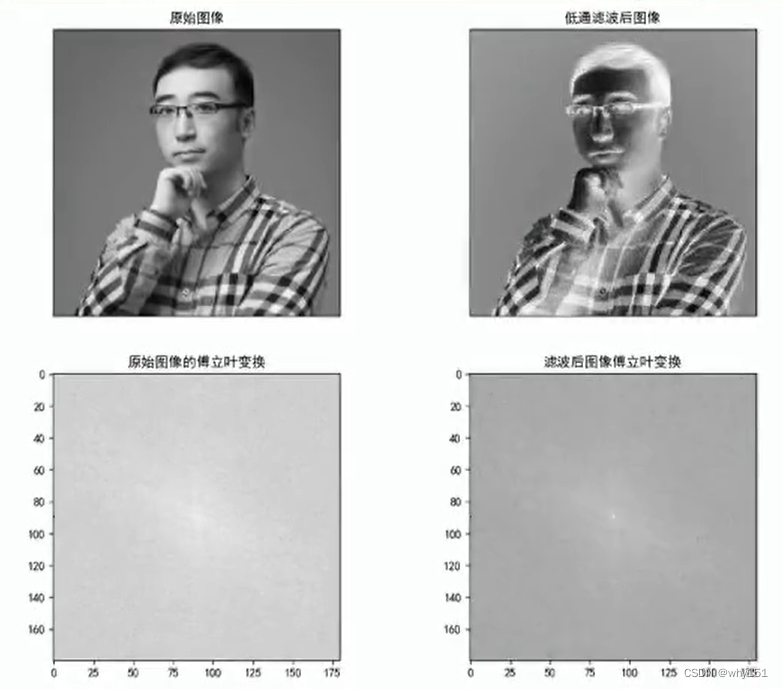
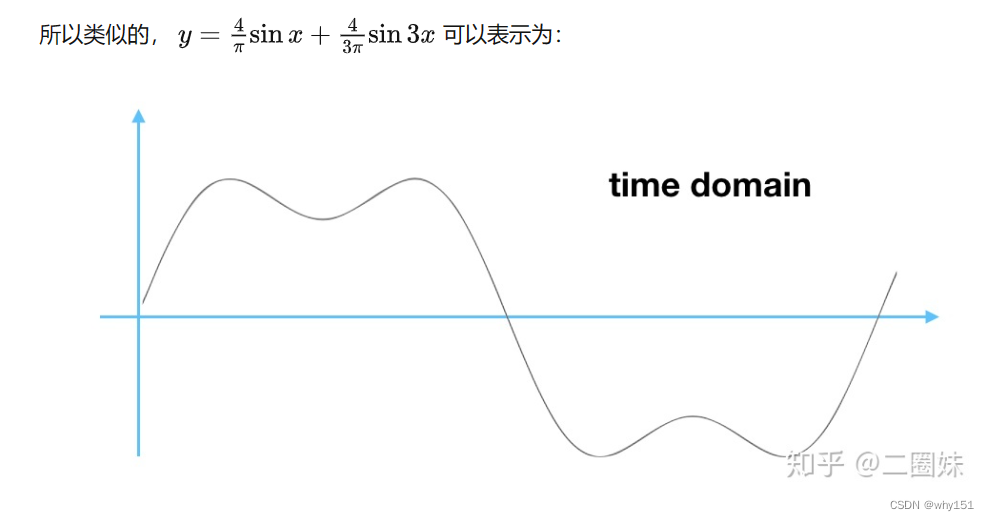
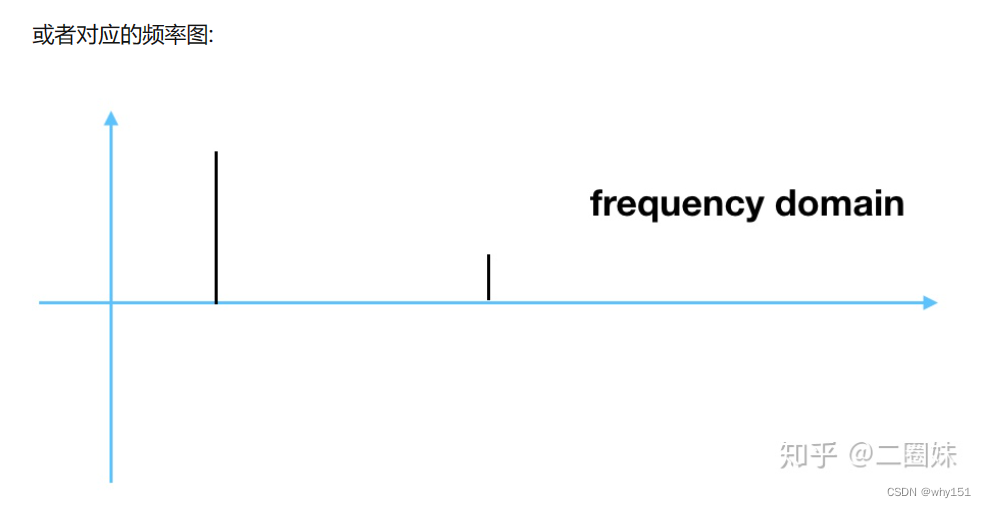
傅里叶级数


**因为一组标准正交基中向量自己和自己做内积为1,和其他向量做内积为0。
所以
q
1
∗
v
q_1*v
q1∗v相当于
q
1
∗
q
1
=
1
,
q
1
∗
q
i
=
0
,
i
!
=
1
q_1*q_1=1,q_1*q_i=0,i!=1
q1∗q1=1,q1∗qi=0,i!=1。**




傅里叶变换(FT)







离散时间傅里叶变换(DTFT)




离散傅里叶变换(DFT)




同时,离散周期傅里叶变换后,计算出来的是一个复数形式,即用正弦和余弦组合的形式近似表示原始信号,所以幅值应该是两者的组合,
A
s
i
n
2
+
A
c
o
s
2
\sqrt{A_{sin^2} + A_{cos^2}}
Asin2+Acos2



实验验证

#! /usr/bin/python3# -*- encoding:utf-8 -*-import matplotlib.pyplot as plt
from matplotlib.pylab import mpl
import numpy as np
from numpy import pi, cos, sin
# 中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=Falsedeftest2():'''
离散傅里叶变换
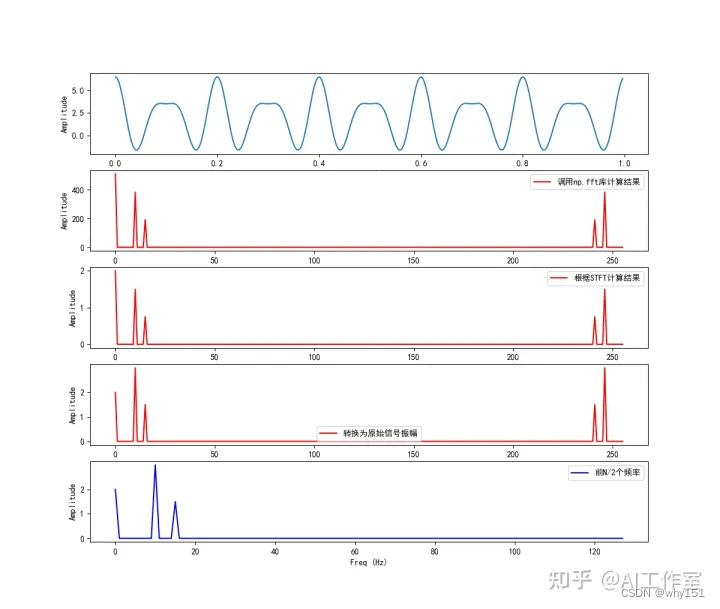
一维时序信号y,它由2V的直流分量(0Hz),和振幅为3V,频率为50Hz的交流信号,以及振幅为1.5V,频率为75Hz的交流信号组成:
y = 2 + 3*np.cos(2*np.pi*50*t) + 1.5*np.cos(2*np.pi*75*t)
然后我们采用256Hz的采样频率,总共采样256个点。
'''
fs =256# 采样频率, 要大于信号频率的两倍
t = np.arange(0,1,1.0/ fs)# 1秒采样fs个点
N =len(t)
freq = np.arange(N)# 频率counter# x = 2 + 3 * cos(2 * pi * 50 * t) + 1.5 * cos(2 * pi * 75 * t) # 离散化后的x[n]
x =2+3* cos(2* pi *10* t)+1.5* cos(2* pi *15* t)# 离散化后的x[n]
X = np.fft.fft(x)# 离散傅里叶变换'''
根据STFT公式原理,实现的STFT计算,做了/N的标准化
'''
X2 = np.zeros(N, dtype=np.complex)# X[n]for k inrange(0, N):# 0,1,2,...,N-1for n inrange(0, N):# 0,1,2,...,N-1# X[k] = X[k] + x[n] * np.exp(-2j * pi * k * n / N)
X2[k]= X2[k]+(1/ N)* x[n]* np.exp(-2j* pi * k * n / N)
fig, ax = plt.subplots(5,1, figsize=(12,12))# 绘制原始时域图像
ax[0].plot(t, x, label='原始时域信号')
ax[0].set_xlabel('Time (s)')
ax[0].set_ylabel('Amplitude')
ax[1].plot(freq,abs(X),'r', label='调用np.fft库计算结果')
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('Amplitude')
ax[1].legend()
ax[2].plot(freq,abs(X2),'r', label='根据STFT计算结果')
ax[2].set_xlabel('Freq (Hz)')
ax[2].set_ylabel('Amplitude')
ax[2].legend()
X_norm = X /(N /2)# 换算成实际的振幅
X_norm[0]= X_norm[0]/2
ax[3].plot(freq,abs(X_norm),'r', label='转换为原始信号振幅')
ax[3].set_xlabel('Freq (Hz)')
ax[3].set_ylabel('Amplitude')
ax[3].set_yticks(np.arange(0,3))
ax[3].legend()
freq_half = freq[range(int(N /2))]# 前一半频率
X_half = X_norm[range(int(N /2))]
ax[4].plot(freq_half,abs(X_half),'b', label='前N/2个频率')
ax[4].set_xlabel('Freq (Hz)')
ax[4].set_ylabel('Amplitude')
ax[4].set_yticks(np.arange(0,3))
ax[4].legend()
plt.show()
test2()
快速傅里叶变换







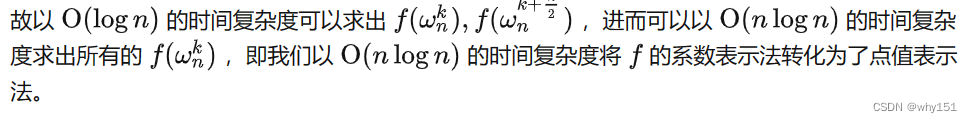




本文转载自: https://blog.csdn.net/weixin_54385104/article/details/128807361
版权归原作者 why151 所有, 如有侵权,请联系我们删除。
版权归原作者 why151 所有, 如有侵权,请联系我们删除。