大多数图神经网络通常在所有节点都可用的特征假设下运行。但是在现实世界的中,特征通常只有部分可用(例如,在社交网络中,只有一小部分用户可以知道年龄和性别)。本文种展示的特征传播是一种用于处理图机器学习应用程序中缺失的特征的有效且可扩展的方法。它很简单,但效果出奇地好。
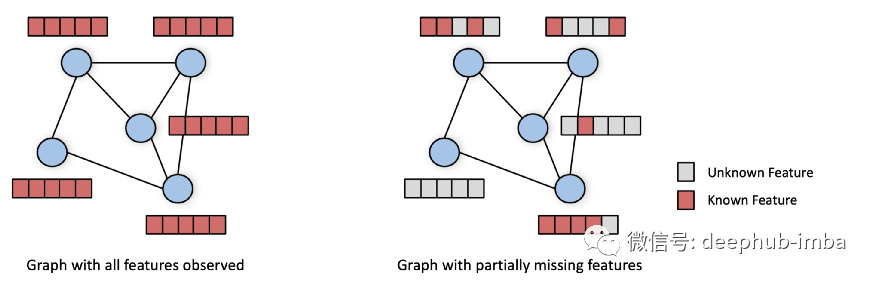
图神经网络 (GNN) 模型通常假设每个节点都有一个完整的特征向量。以一个 2 层 GCN 模型 [1] 为例,它具有以下形式:
Z = A σ(AXW₁) W₂
该模型的两个输入是编码图结构(归一化的)邻接矩阵 A 和作为行的节点特征的特征矩阵 X,输出为节点嵌入 Z。GCN 的每一层执行节点特征变换(参数化可学习矩阵 W₁ 和 W₂),然后将转换后的特征向量传播到相邻节点。这里面一个重要的概念是:GCN 假设 X 中的所有条目都被观察到。
但是在现实世界的场景中,经常会看到一些节点特征可能会缺失。例如,年龄、性别等人口统计信息可能仅对一小部分社交网络用户可用,而内容特征通常仅对最活跃的用户呈现。例如在推荐系统中并非所有产品都有与之相关的完整描述,这使得情况变得更加严重,随着人们对数字隐私的认识不断提高,越来越多的数据只有在用户明确同意的情况下才能获得。
根据上面的描述,特征矩阵都有缺失值的,大多数现有的 GNN 模型都不能直接应用。最近的几项工作派生了能够处理缺失特征的 GNN 模型(例如 [2-3]),但是这些模型在缺失特征率很高(>90%)的情况下受到影响,并且不能扩展到具有超过几百万条边的图.
在 Maria Gorinova、Ben Chamberlain (Twitter)、Henry Kenlay 和 Xiaowen Dong (Oxford) 合着的一篇新论文 [4] 中,提出了特征传播 (FP) [4] 作为一种简单但高效且令人惊讶的有效解决方案。简而言之,FP 通过在图上传播已知特征来重构缺失的特征。然后可以将重建的特征输入任何 GNN 以解决下游任务,例如节点分类或链接预测。
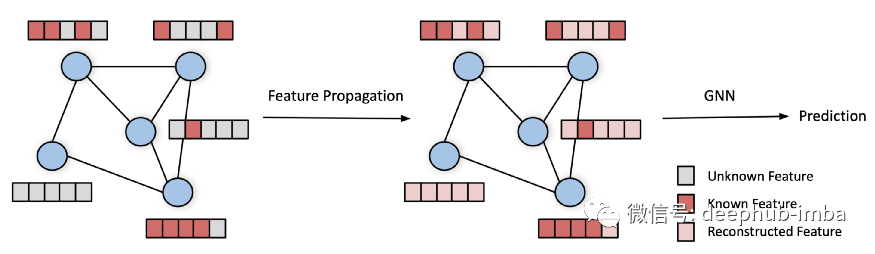
特征传播框架。输入是缺少节点特征的图(左)。在初始步骤中,特征传播通过迭代地扩散图中的已知特征来重构缺失的特征(中)。随后,图和重建的节点特征被输入到下游 GNN 模型中,然后产生预测(右)。
传播步骤非常简单:首先,未知特征用任意值初始化[5]。通过应用(归一化的)邻接矩阵来传播特征,然后将已知特征重置为其真实值。我们重复这两个操作,直到特征向量收敛[6]。

特征传播是一种简单且令人惊讶的强大方法,用于在缺少特征的图上进行学习。特征的每个坐标都被单独处理(x 表示 X 的一列)。
FP 可以从数据同质性(“平滑性”)的假设中推导出来,即邻居往往具有相似的特征向量。同质性的水平可以使用Dirichlet energy来量化,这是一种测量节点特征与其邻居平均值之间的平方差的二次形式。Dirichlet energy[7] 的梯度流是图热扩散方程,以已知特征作为边界条件。FP 是使用具有单位步长的显式前向 Euler 方案作为该扩散方程的离散化获得的 [8]。
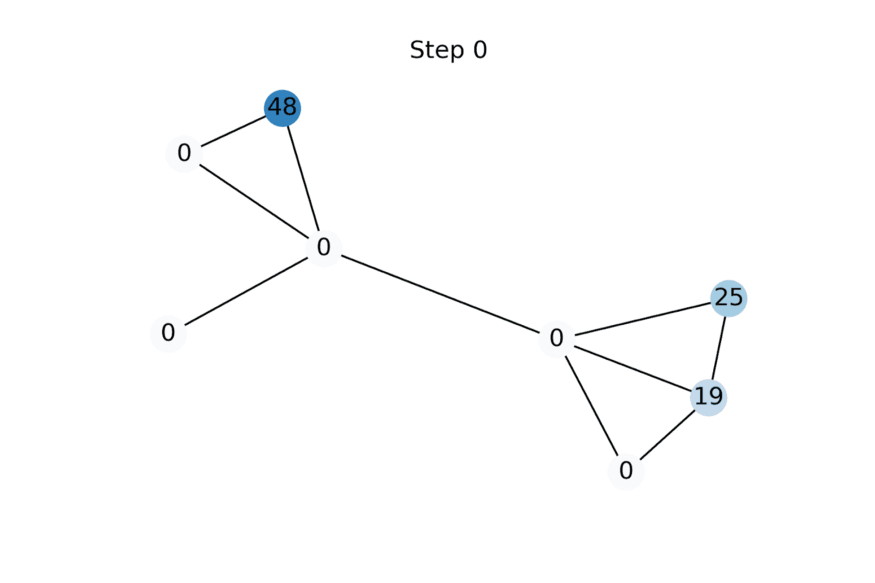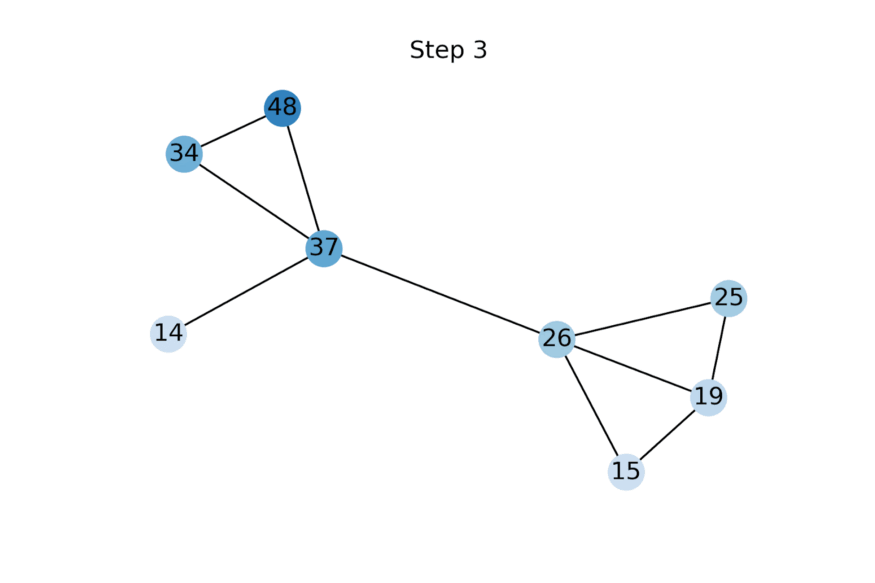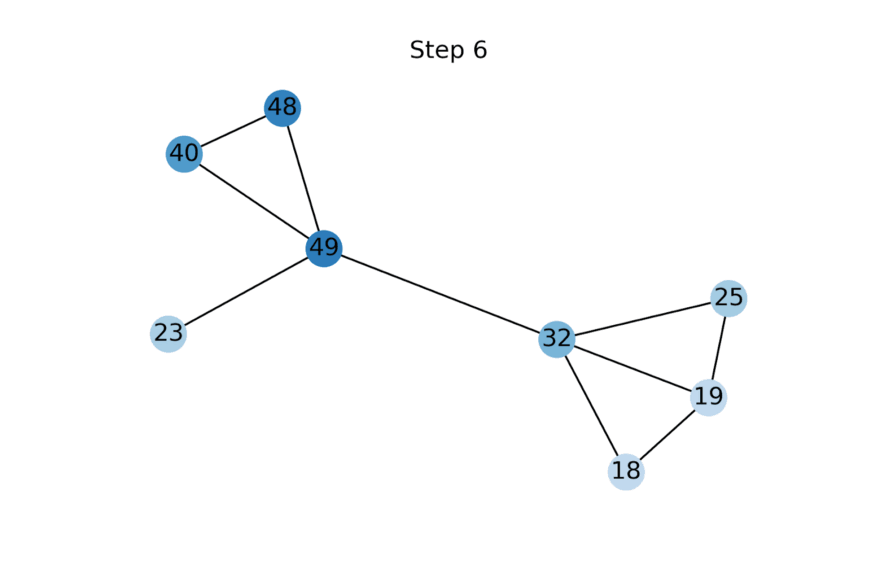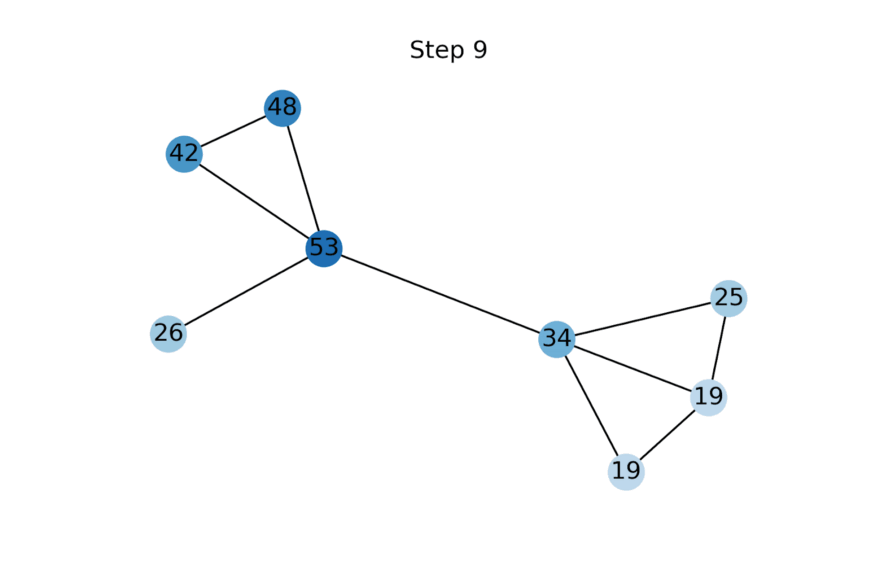
动画展示了随着特征传播的更多迭代应用而标量节点特征的演变示例。未知特征被初始化为零,但很快收敛到使给定图上的Dirichlet energy最小化的值。
特征传播与标签传播(LP)[9]相似。关键区别在于 LP 是一种与特征无关的方法,它通过在图中传播已知标签来直接预测每个节点的类,而FP 用于首先重建缺失的节点特征,然后将其馈送到下游 GNN。这使得 FP 能够利用观察到的特征,并在所有基准测试中都优于 LP。在实践中经常发生带标签的节点集和具有特征的节点集不一定完全重叠,因此这两种方法并不总是可以直接比较。
论文中使用七个标准节点分类基准对 FP 进行了广泛的实验验证,其中随机删除了可变部分的节点特征(独立于每个通道)。FP 后跟一个 2 层 GCN 在重建特征上的表现明显优于简单的基线以及最新的最先进的方法 [2-3]。
FP 在特征缺失率高 (>90%) 的情况下尤为突出,而所有其他方法往往会受到影响。例如,即使丢失了 99% 的特征,与所有特征都存在的相同模型相比,FP 平均仅损失约 4% 的相对准确度。
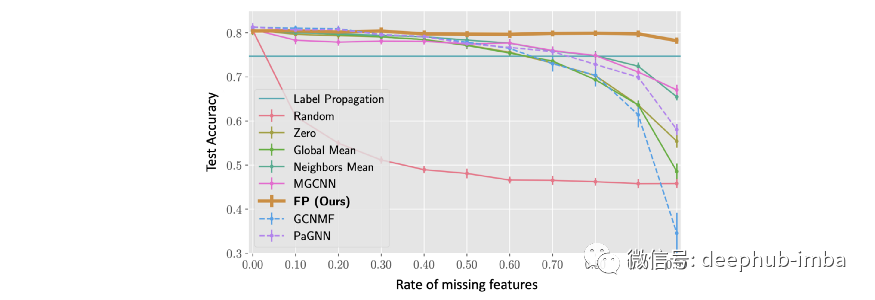
Cora 数据集上不同特征缺失率的节点分类准确度(从 0% 是大多数 GNN 的标准状态到 99% 的极端情况)。
FP 的另一个关键特点是它的可扩展性:其他方法无法扩展到具有几百万条边的图之外,但 FP 可以扩展到十亿条边的图。作者用了不到一小时的时间在内部 Twitter 图表上运行它,使用单台机器大约有 10 亿个节点和 100 亿条边。
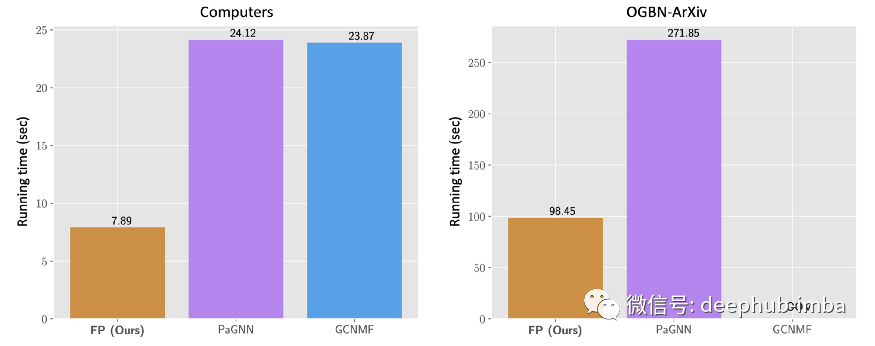
FP+GCN 和最新最先进的方法 GCNMF 和 PaGNN [2-3] 的运行时间(以秒为单位)。FP+GCN 比其他两种方法快 3 倍。GCNMF 在 OGBN-Arxiv 上出现内存不足 (OOM),而 GCNMF 和 PaGNN 在 OGBN-Products(约 123M 边)上出现 OOM,其中 FP 的重建部分(无需训练下游模型)仅需约 10 秒。
FP 的当前限制之一是它在heterophilic graphs上效果不佳,即邻居具有不同特征的图。这并不奇怪,因为 FP 源自同质假设(通过扩散方程最小化 Dirichlet energy)。FP 假设不同的特征通道是不相关的,这在现实生活中很少见。但是可以通过替代更复杂的扩散机制,同时满足这两个限制。
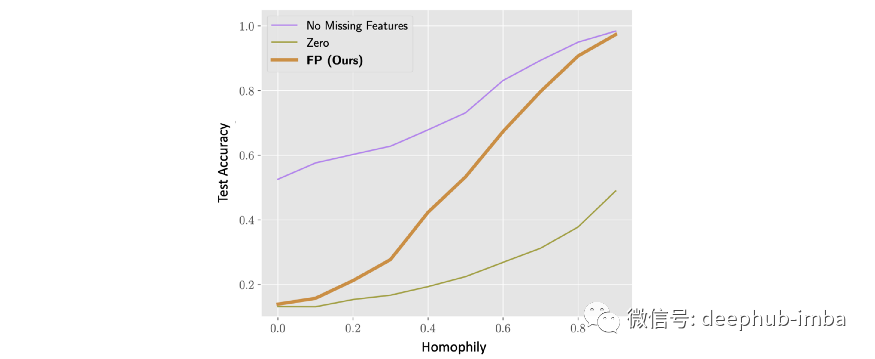
当 99% 的特征缺失时,具有各种同质性水平的合成图上的节点分类准确度(0 是极度异质性,1 是极度同质性)。虽然在高度同质性设置中 FP 的表现几乎与具有完整特征的情况一样好,但在低同质性设置中,两者之间的差距很大,并且 FP 的性能恶化到一个简单的基线,其中缺失的特征被替换为 零。
尽管在实际应用中无处不在,但在缺少节点特征的图上学习是一个几乎未被探索的研究领域。特征传播模型是提高在缺少节点特征的图上学习能力的重要一步,它还提出了关于在这种情况下学习的理论能力的深刻问题。FP 的简单性和可扩展性,以及与更复杂的方法相比的惊人的好结果,即使在极端缺失的特征状态下,也使其成为大规模工业应用的良好候选者。
引用
[1] T. Kipf and M. Welling, Semi-Supervised Classification with Graph Convolutional Networks (2017), ICLR.
[2] H. Taguchi et al., Graph Convolutional Networks for Graphs Containing Missing Features (2020), Future Generation Computer Systems.
[3] X. Chen et al., Learning on Attribute-Missing Graphs (2020), arXiv:2011.01623
[4] E. Rossi et al., On the Unreasonable Effectiveness of Feature propagation in Learning on Graphs with Missing Node Features (2021), arXiv:2111.12128
[5] We show that the algorithm converges to the same solution, regardless of the initialisation of the unknown values. However, a different initialisation may lead to a different number of iterations necessary to converge. In our experiments we initialise the unknown values to zero.
[6] We found ~40 iterations to be sufficient for convergence on all datasets we experimented with.
[7] A gradient flow can be seen as a continuous analogy of gradient descent in variational problems. It arises from the optimality conditions (known in the calculus of variations as Euler-Lagrange equations) of a functional.
[8] B. Chamberlain et al., GRAND: Graph Neural Diffusion (2021), ICML. See also the accompanying blog post.
[9] X. Zhu and Z. Ghahramani, Learning from labeled and unlabeled data with label propagation (2002), Technical Report.
作者:Michael Bronstein