一、前言
二叉树的定义:二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分
在解决二叉树问题时,我们的利器就是“递归”,但是递归这种思想掌握起来常常让大家叫苦不迭,本篇文章将从易到难,深入浅出地讲解二叉树问题
对于二叉树,我们首先要了解几个最基本的公式:
1.若规定根节点的层数为1,则层数i最多有 2^(i-1)个结点
2.若规定根节点的深度为1,则深度为k的二叉树最多拥有 2^k-1个结点
3.对具有N个结点的完全二叉树而言,深度为log 2(N+1) 向上取整
4.我们如果定义度数为0的结点数量为n0,度数为2的结点数量为n2,则n0=n2+1
如果你已经对二叉树的性质很了解,做完以下这些题目,你将成为彻彻底底的二叉树大神!
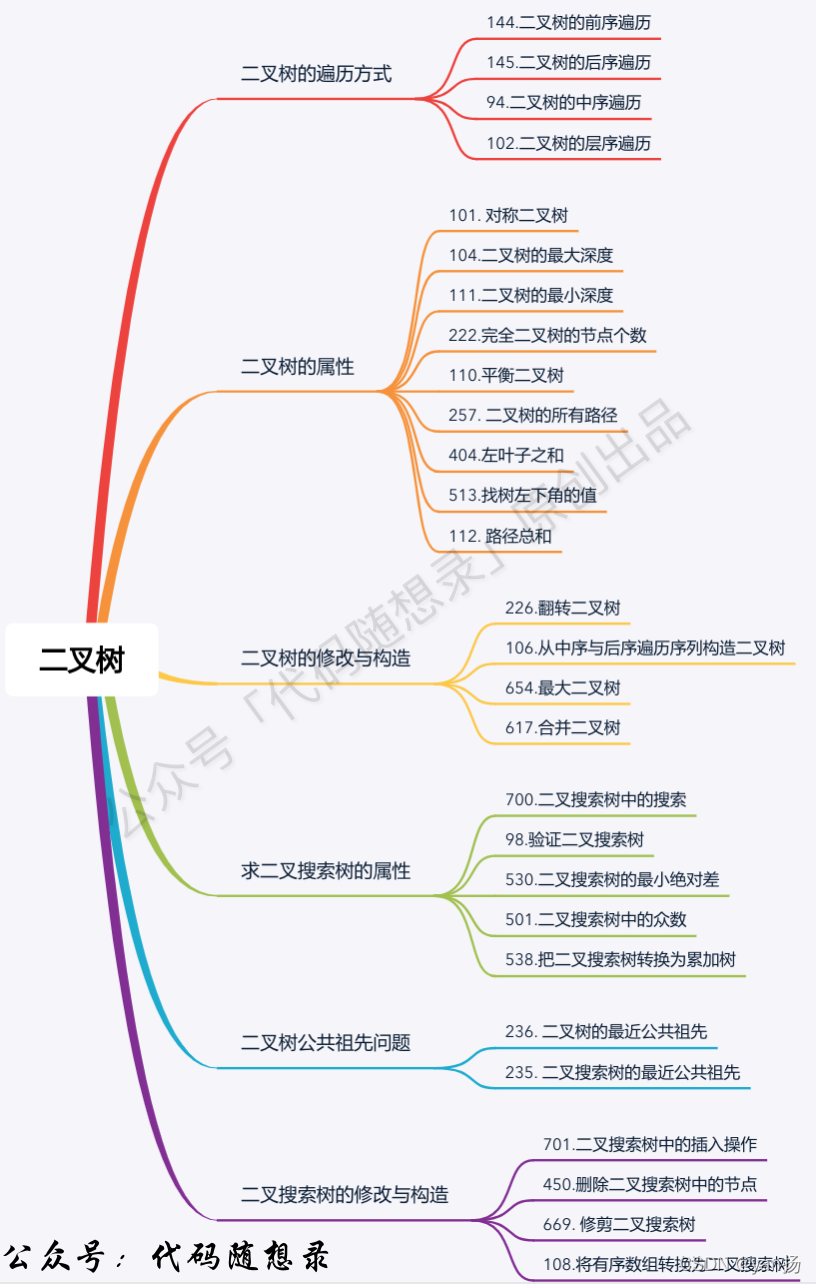
图片来源:代码随想录
二、二叉树的遍历
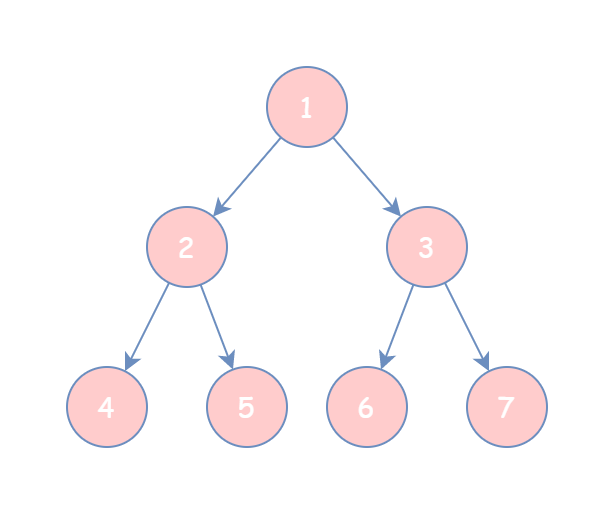
对于这颗二叉树:
1)如果我们按照前序遍历 即根结点-> 左孩子->右孩子的顺序遍历 则结果为 1,2,3,4,5,6,7
2)如果我们按照中序遍历 即左孩子-> 根节点->右孩子的顺序遍历 则结果为 4,2,5,1,6,3,7
3)如果我们按照后序遍历 即左孩子-> 右孩子->根节点的顺序遍历 则结果为 4,5,2,6,7,3,1
4)如果我们按照层序遍历 每一层从左至右 则结果为 1,2,3,4,5,6,7
1、前序遍历
1)递归解法:
leetcode前序遍历:144. 二叉树的前序遍历 - 力扣(LeetCode) (leetcode-cn.com)https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
public static void preOrderRecur(TreeNode head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
2)迭代解法:
本质上是模拟递归,因为在递归时系统帮我们调用了栈,我们用stack来模拟系统栈
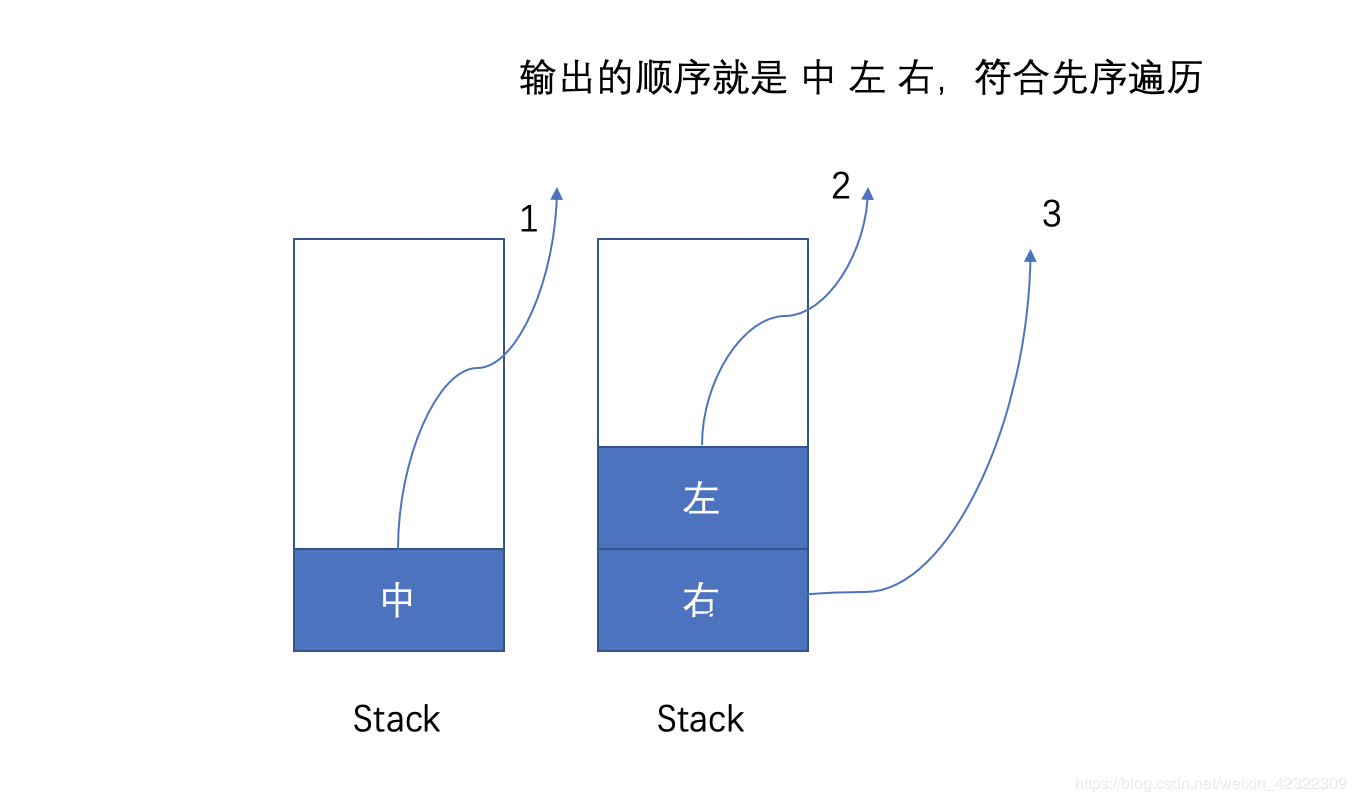
我们知道前序的顺序是 根 左 右 因此我们先把根节点加入到栈中 ,再加入右节点,再加入左节点
再逐一从栈中弹出 顺序就是 根 左 右
public class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res=new ArrayList<>();
if (root==null) return res;
Deque<TreeNode> stack=new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()){
root=stack.pop();
res.add(root.val);
if (root.right!=null){
stack.push(root.right);
}
if (root.left!=null){
stack.push(root.left);
}
}
return res;
}
}
2、中序遍历
1)递归解法:
leetcode中序遍历:
- 二叉树的中序遍历 - 力扣(LeetCode) (leetcode-cn.com)https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
public static void preOrderRecur(TreeNode head) {
if (head == null) {
return;
}
preOrderRecur(head.left);
System.out.print(head.value + " ");
preOrderRecur(head.right);
}
2)迭代解法:
1.同理创建一个Stack,然后按 左 中 右的顺序输出节点。
2.栈中不断添加根节点机它的左节点,我们先把树中最左的元素找到(这个元素一定是null)然后从栈中弹出它的父节点,再处理父节点的右子树,再不断弹出,再处理右节点
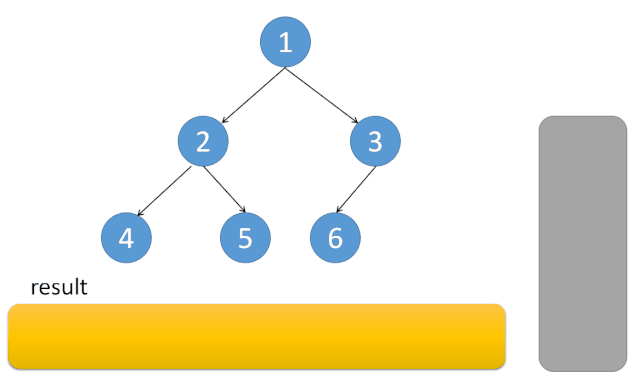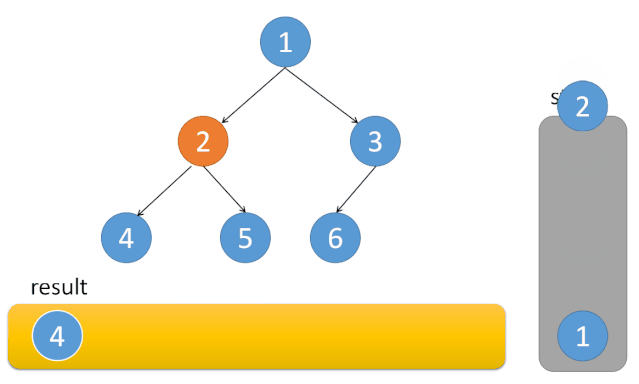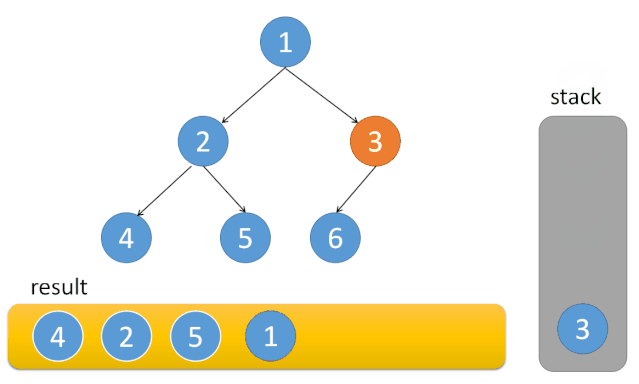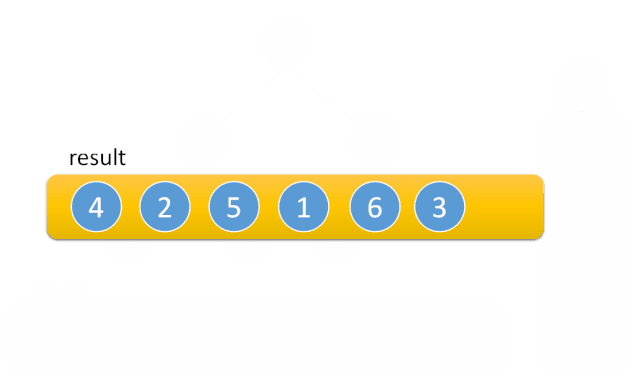
代码如下:
public List<Integer> inorderTraversal(TreeNode root) {
List res=new ArrayList();
Deque<TreeNode> stack=new LinkedList();
while (root!=null||!stack.isEmpty()){
while (root!=null){//先把节点的左节点都添加入栈
stack.push(root);
root=root.left;
}//退出循环说明此时节点的左节点是null,那么我们从栈中弹出一个元素,添加入返回的list
root=stack.pop();//获得节点入list
res.add(root.val);
root=root.right;//查看此时root是不是null,不是null就进入循环,是null,root就重新从栈中弹出元素
}
return res;
}
3、后序遍历
leetcode后序遍历:
- 二叉树的后序遍历 - 力扣(LeetCode) (leetcode-cn.com)https://leetcode-cn.com/problems/binary-tree-postorder-traversal/
1)递归解法:
public static void postOrderRecur(TreeNode head) {
if (head == null) {
return;
}
postOrderRecur(head.left);
postOrderRecur(head.right);
System.out.print(head.value + " ");
}
2)迭代写法:
其实无论是前序,中序,或后序,他们的遍历顺序都是一样的,无非就是第几次经过的时候把结点输出(返回)前序是第一次遇到就输出 中序是第二次 后序是第三次
在遍历的过程中 ,我们不断把结点加入到栈中,当我们从栈中弹出结点的时候其实是第二次来到结点,但由于已经弹出了结点,导致无法第三次来到结点,而后序遍历要求我们第三次来到结点时打印 这时我们思考 是否可以第二次来到结点的时候只查看 而不打印 只有第三次来到结点时才打印?
第三次来到结点的条件:
1)结点没有右子树,只能来到两次
2)上一次从栈中弹出的结点是来自当前结点的右节点
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res=new ArrayList<>();
if (root==null) return res;
Deque<TreeNode> stack=new LinkedList<>();
TreeNode pre=null;
while(!stack.isEmpty()||root!=null){
while (root!=null){
stack.push(root);
root=root.left;
}
root = stack.pop();
if (root.right == null || root.right == pre) {
res.add(root.val);
pre = root;
root = null;
} else {
stack.push(root);
root = root.right;
}
}
return res;
}
其实后序遍历还可以利用一个辅助栈,之前我么前序遍历的时候说到过,只要利用 先右再左的方式压栈就可以实现 中 左 右的输出 而我们利用辅助栈 先把中压入辅助栈底 再把 左压入栈 再压入右 最后全部输出压入辅助栈 则辅助栈的信息就是 左 右 中
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
//首先我们需要两个栈
Deque<TreeNode> stack1=new LinkedList<>();
Deque<TreeNode> stack2=new LinkedList<>();
List<Integer> res=new ArrayList<>();
if(root==null) return res;
stack1.push(root);
while(!stack1.isEmpty()){
root=stack1.pop();
stack2.push(root);
if(root.left!=null) stack1.push(root.left);
if(root.right!=null) stack1.push(root.right);
}
while(!stack2.isEmpty()){
res.add(stack2.pop().val);
}
return res;
}
}
虽然这种方式可以巧妙地实现后序遍历,但我还是觉得第一种非递归解法是更需要我们掌握的,因为前序 中序 后序 地唯一差别其实是 我么究竟第几次来到当前结点 掌握这种思想 更利于我们掌握接下来地morris遍历
4、层序遍历
简单来说,层次遍历就是把二叉树分层,每一层从左到右遍历
leetcode中有一篇大神的题解对BFS和DFS地讲解深入浅出 讲的很清晰!这里推给大家:
BFS 的使用场景总结:层序遍历、最短路径问题 - 二叉树的层序遍历 - 力扣(LeetCode) (leetcode-cn.com)https://leetcode-cn.com/problems/binary-tree-level-order-traversal/solution/bfs-de-shi-yong-chang-jing-zong-jie-ceng-xu-bian-l/
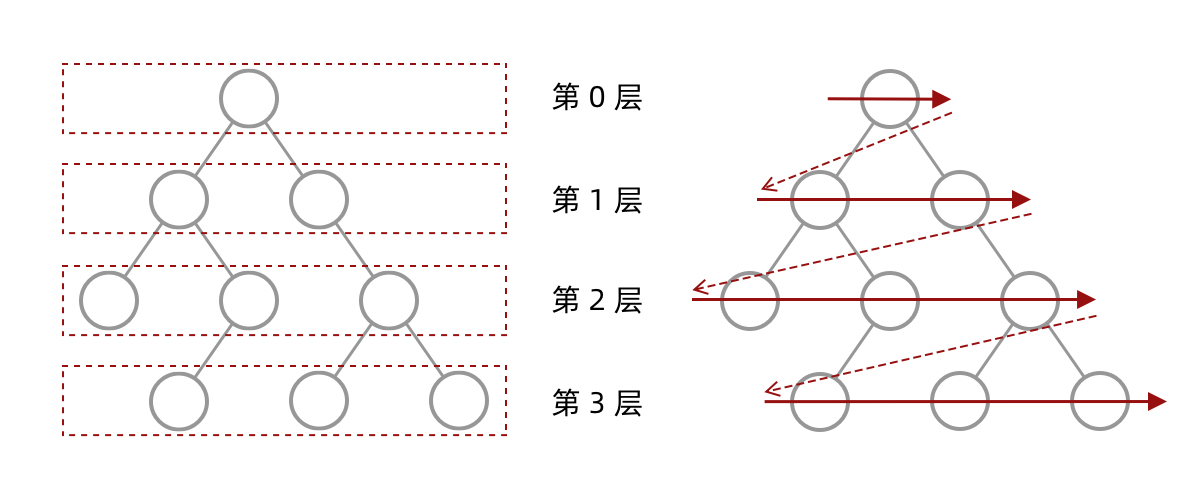
乍一看,这个层序遍历不就是BFS吗?是的,BFS和层序遍历的确差不多,但我们要知道在BFS中没有“层”信息,无法按层输出
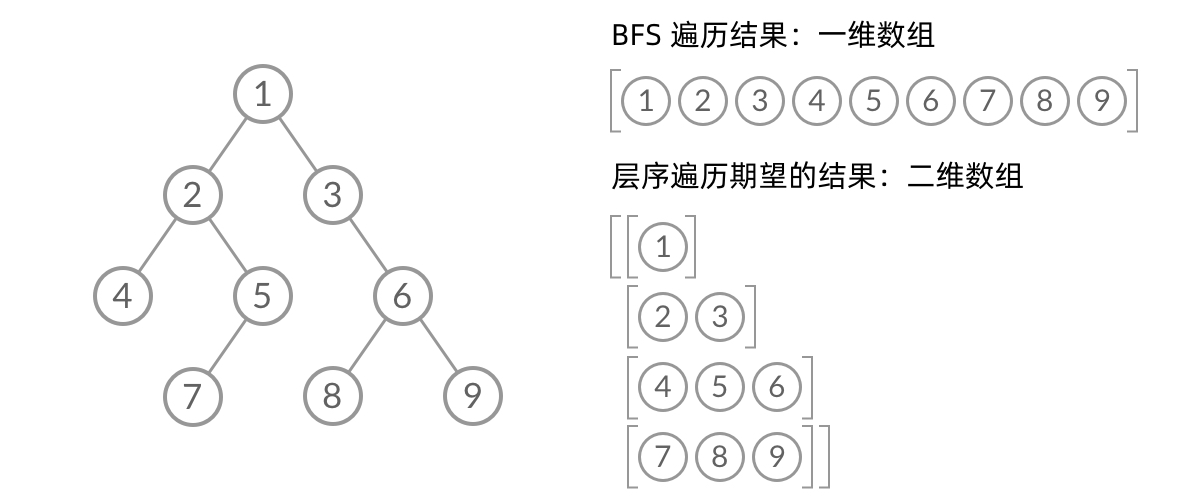
如何 对BFS结果进行分层呢?
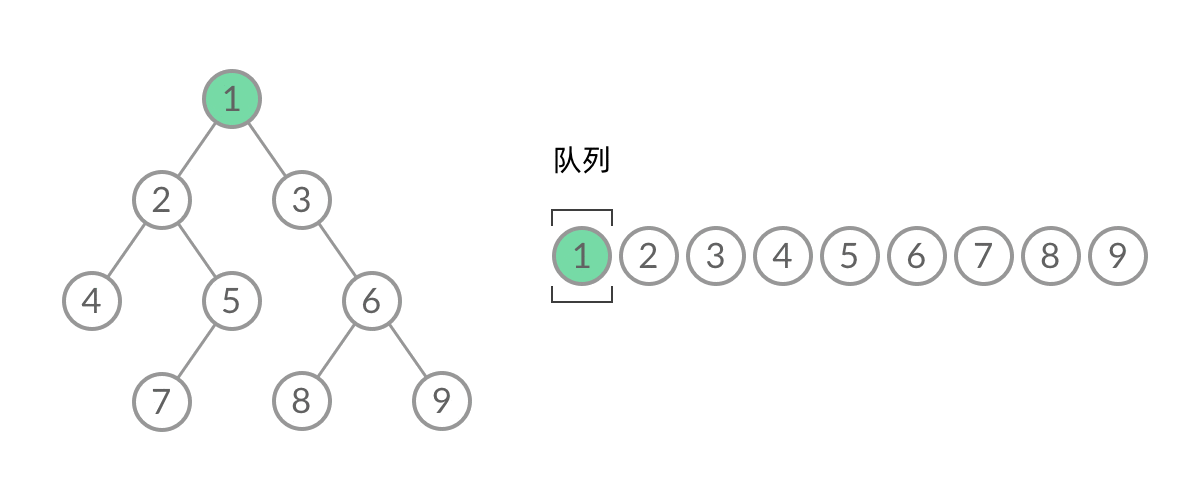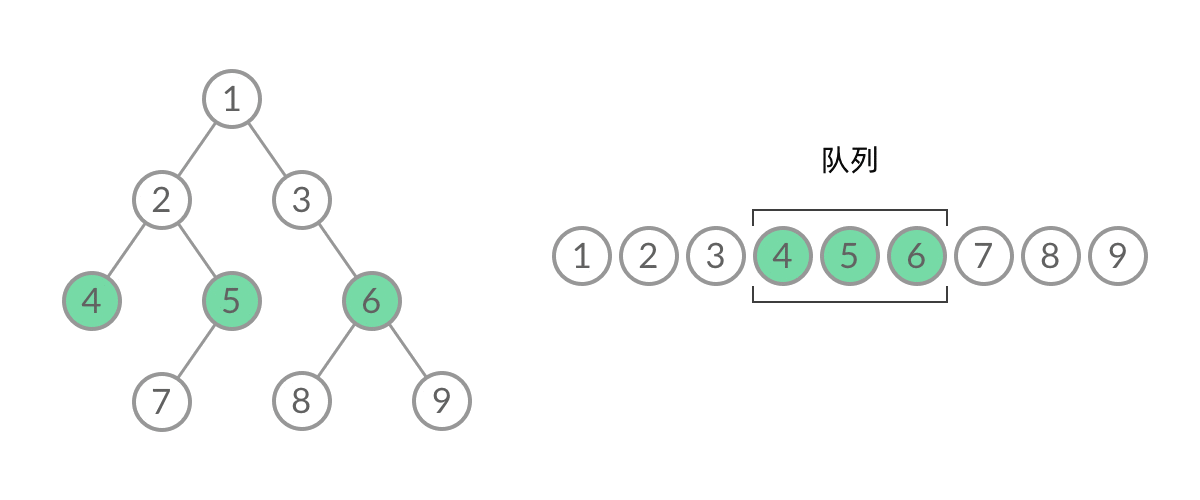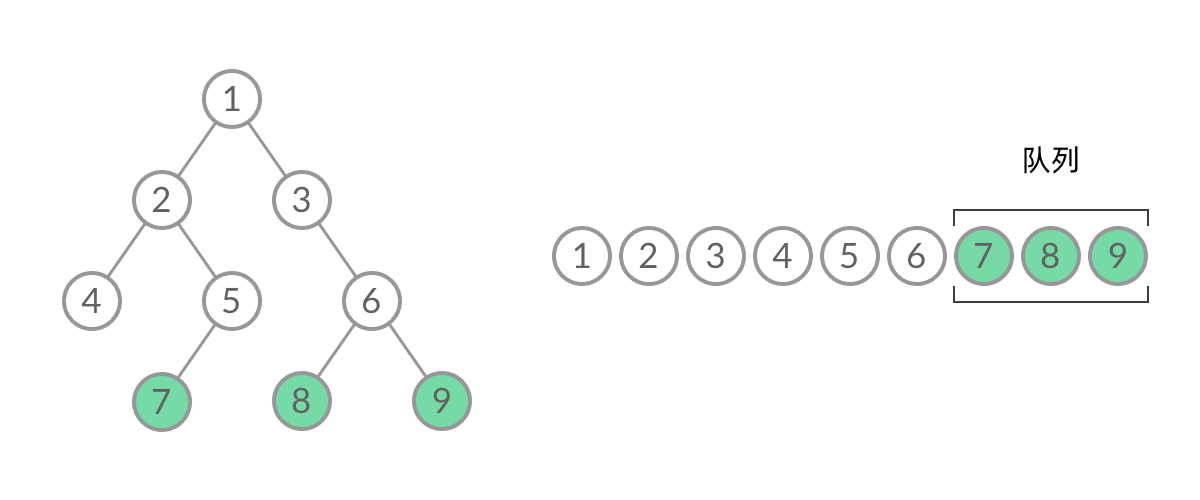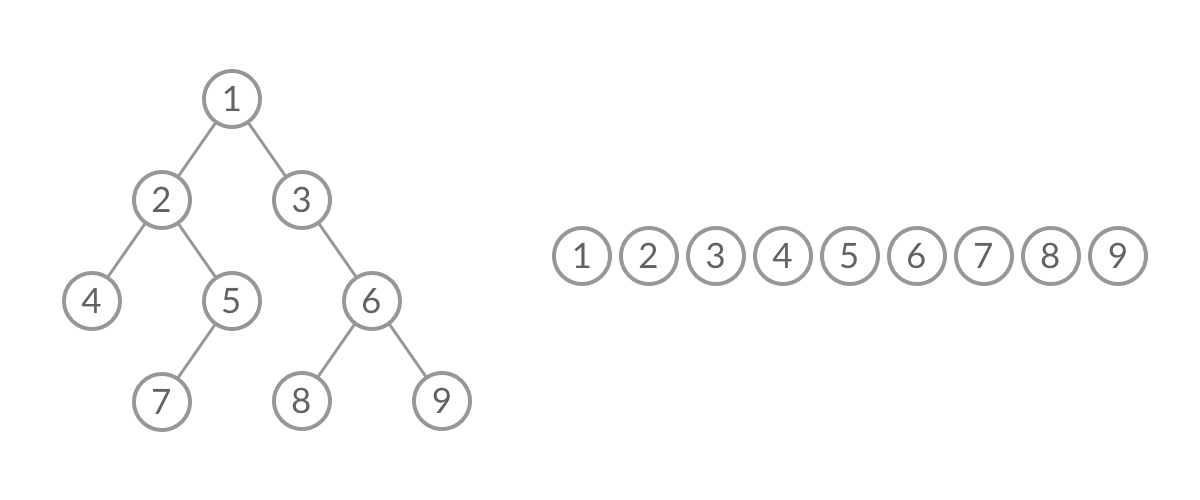
我们观察BFS过程中结点进队列 出队列的过程:
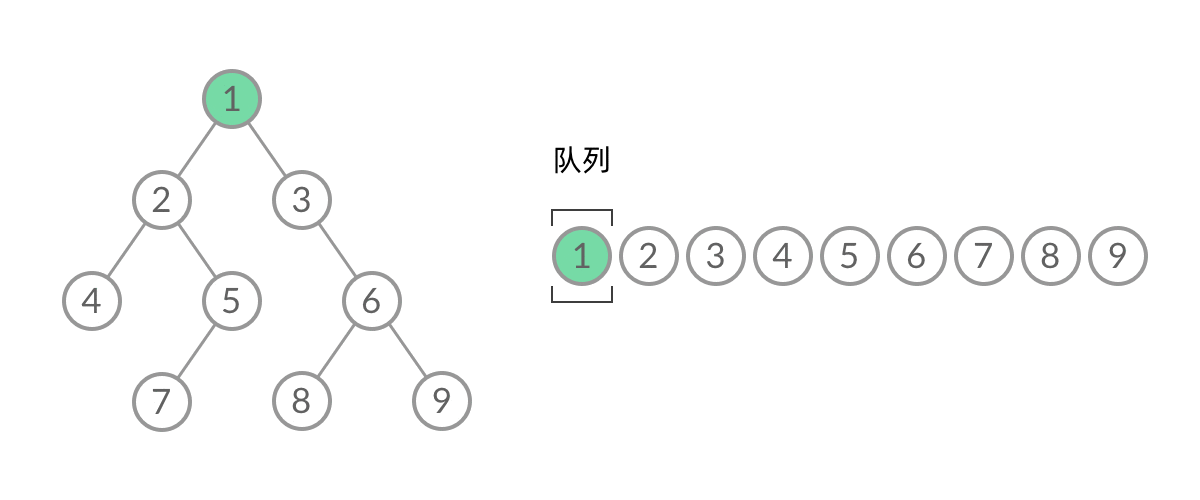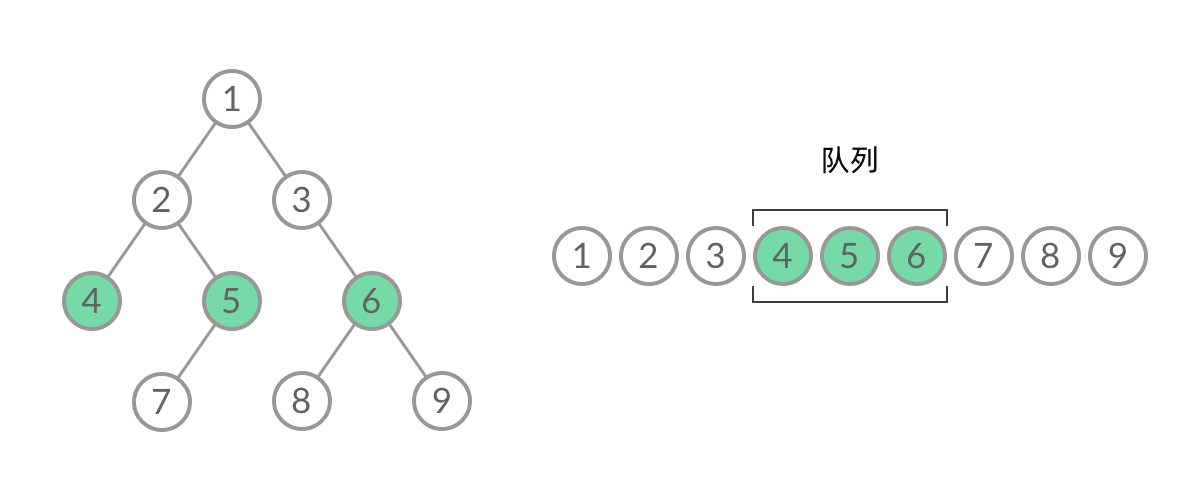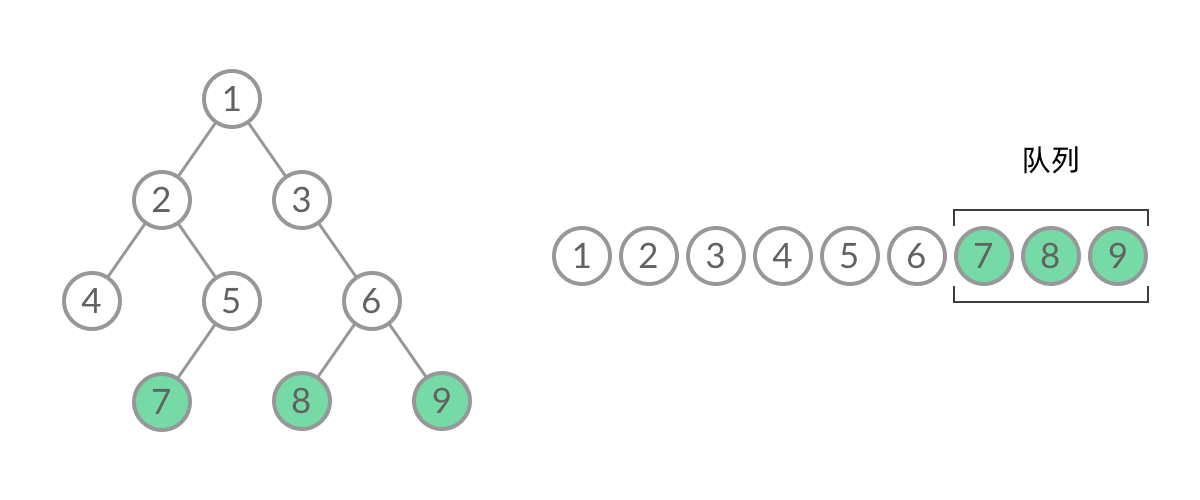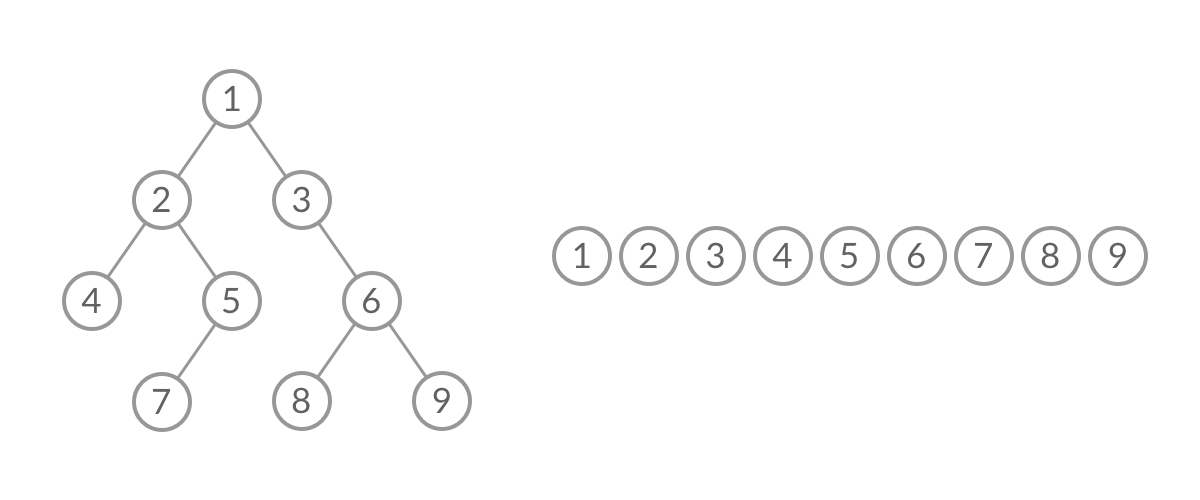
截取BFS中一个过程:
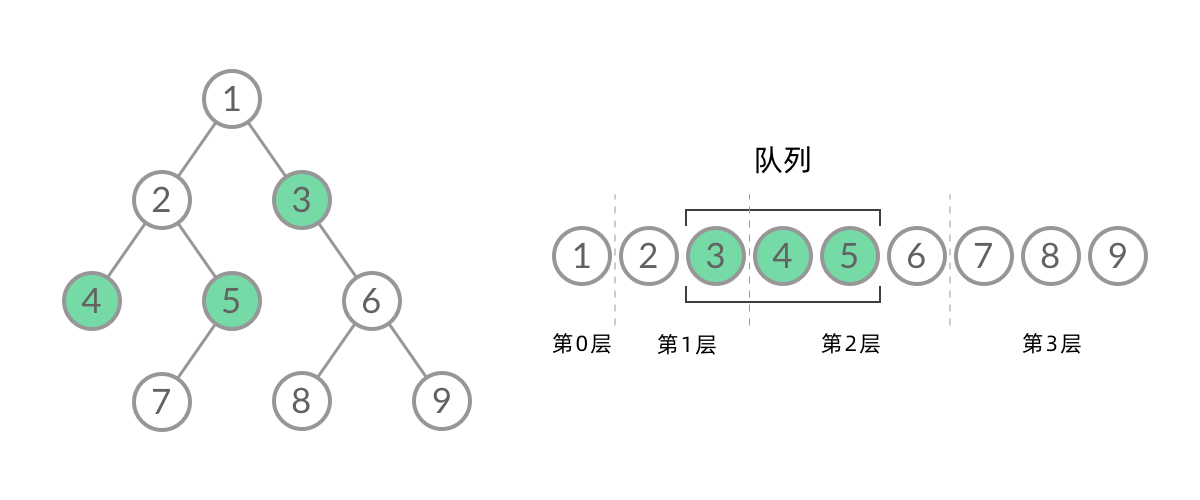
可以看到,此时队列中的结点是 3、4、5,分别来自第 1 层和第 2 层。这个时候,第 1 层的结点还没出完,第 2 层的结点就进来了,而且两层的结点在队列中紧挨在一起,我们无法区分队列中的结点来自哪一层。
因此,我们需要稍微修改一下代码,在每一层遍历开始前,先记录队列中的结点数量 n(也就是这一层的结点数量),然后一口气处理完这一层的 n 个结点。
// 二叉树的层序遍历
void bfs(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()) {
int n = queue.size();
for (int i = 0; i < n; i++) {
// 变量 i 无实际意义,只是为了循环 n 次
TreeNode node = queue.poll();
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
}
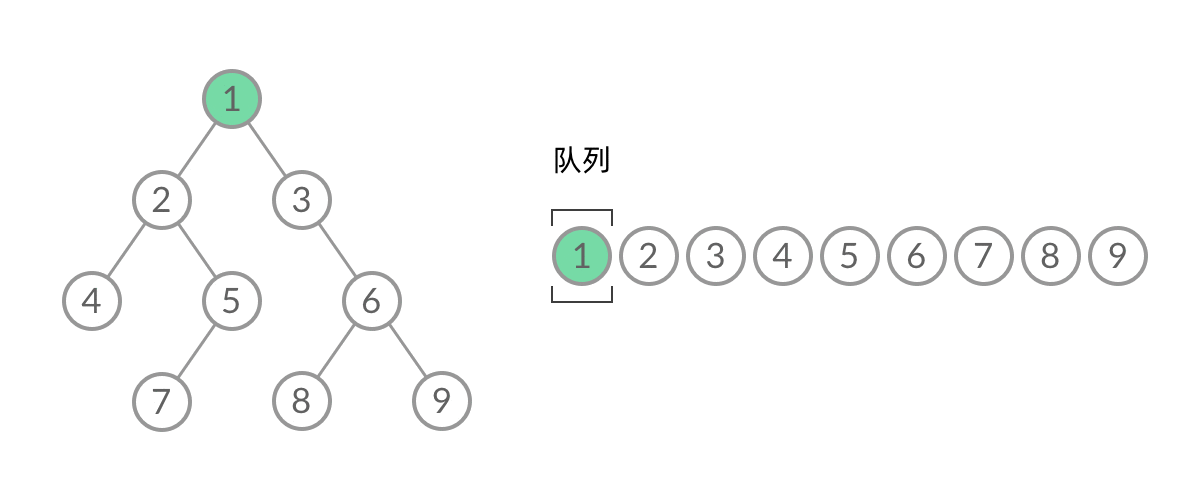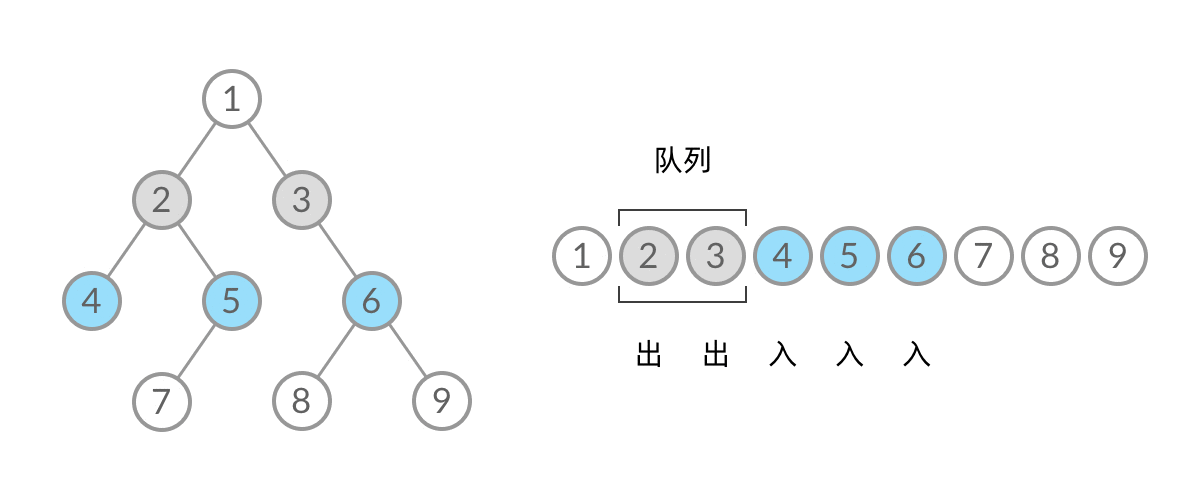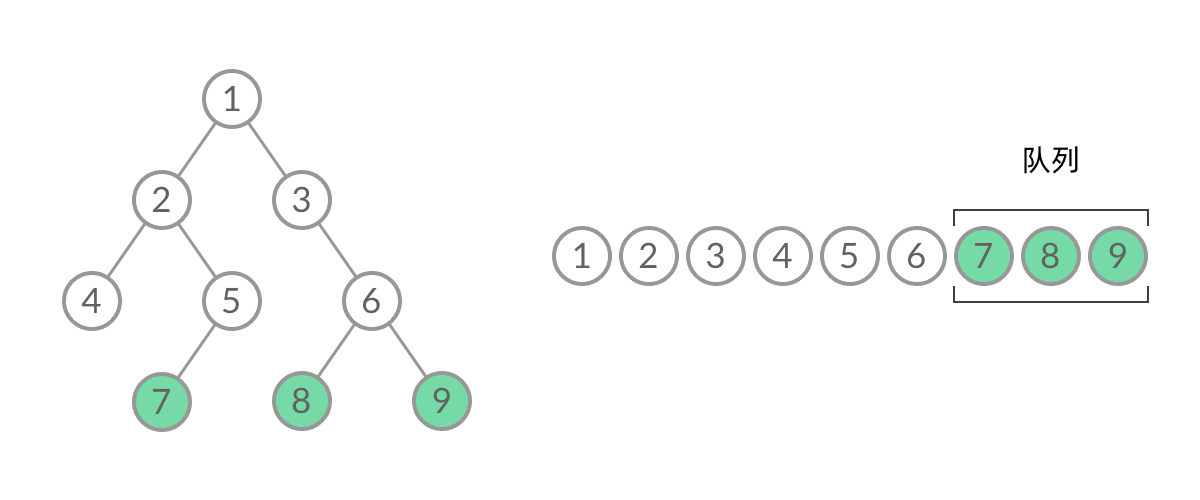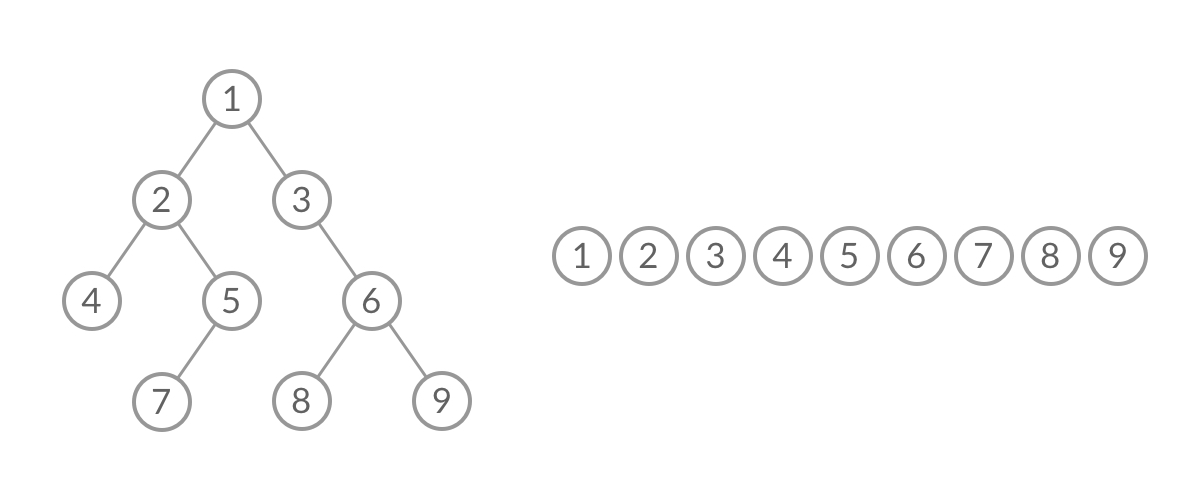
这样,我们就将 BFS 遍历改造成了层序遍历。在遍历的过程中,结点进队列和出队列的过程为:
5、Morris遍历
有一种巧妙的方法可以在线性时间内,只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris 遍历。
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减。其前序遍历规则总结如下:
1)新建临时节点,令该节点为 root;
2)如果当前节点的左子节点为空,将当前节点加入答案,并遍历当前节点的右子节点;
- 如果当前节点的左子节点不为空,在当前节点的左子树中找到当前节点在中序遍历下的前驱节点:
如果前驱节点的右子节点为空,将前驱节点的右子节点设置为当前节点。然后将当前节点加入答案,并将前驱节点的右子节点更新为当前节点。当前节点更新为当前节点的左子节点。
如果前驱节点的右子节点为当前节点,将它的右子节点重新设为空。当前节点更新为当前节点的右子节点。
4)重复步骤 2 和步骤 3,直到遍历结束。
这样我们利用 Morris 遍历的方法,前序遍历该二叉树,即可实现线性时间与常数空间的遍历。
我们知道 前序 中序 后序的唯一区别就是 第几次来到该节点时打印 那么我么就可以在Morris
遍历的基础上选择第几次打印即可:
前序遍历代码:(第一次来到结点时打印):
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res=new ArrayList<>();
TreeNode cur=root;
TreeNode mostRight=null;//cur左子树上的最右结点
while (cur!=null){
mostRight=cur.left;
if (mostRight!=null){
while (mostRight.right!=null&&mostRight.right!=cur){
mostRight=mostRight.right;
}
if (mostRight.right==null){//第一次来到该节点
res.add(cur.val);
mostRight.right=cur;
cur=cur.left;
continue;
}else {
mostRight.right=null;//第二次来到该节点
}
}else {
res.add(cur.val);
}
cur=cur.right;//如果左子树为空 就往右走
}
return res;
}
}
中序遍历代码:(第二次来到结点时打印):
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res=new ArrayList<>();
TreeNode cur=root;
TreeNode mostRight=null;//cur左子树上的最右结点
while (cur!=null){
mostRight=cur.left;
if (mostRight!=null){
while (mostRight.right!=null&&mostRight.right!=cur){
mostRight=mostRight.right;
}
if (mostRight.right==null){//第一次来到该节点
mostRight.right=cur;
cur=cur.left;
continue;
}else {
res.add(cur.val);
mostRight.right=null;//第二次来到该节点
}
}else {
res.add(cur.val);
}
cur=cur.right;//如果左子树为空 就往右走
}
return res;
}
}
后序遍历:要求第三次来到结点时打印 但由于我们一个结点只能来到两次 这里有一个要求:当一个节点能回到自己两次且第二次回到自己时 我们逆序打印该节点左树的右边界
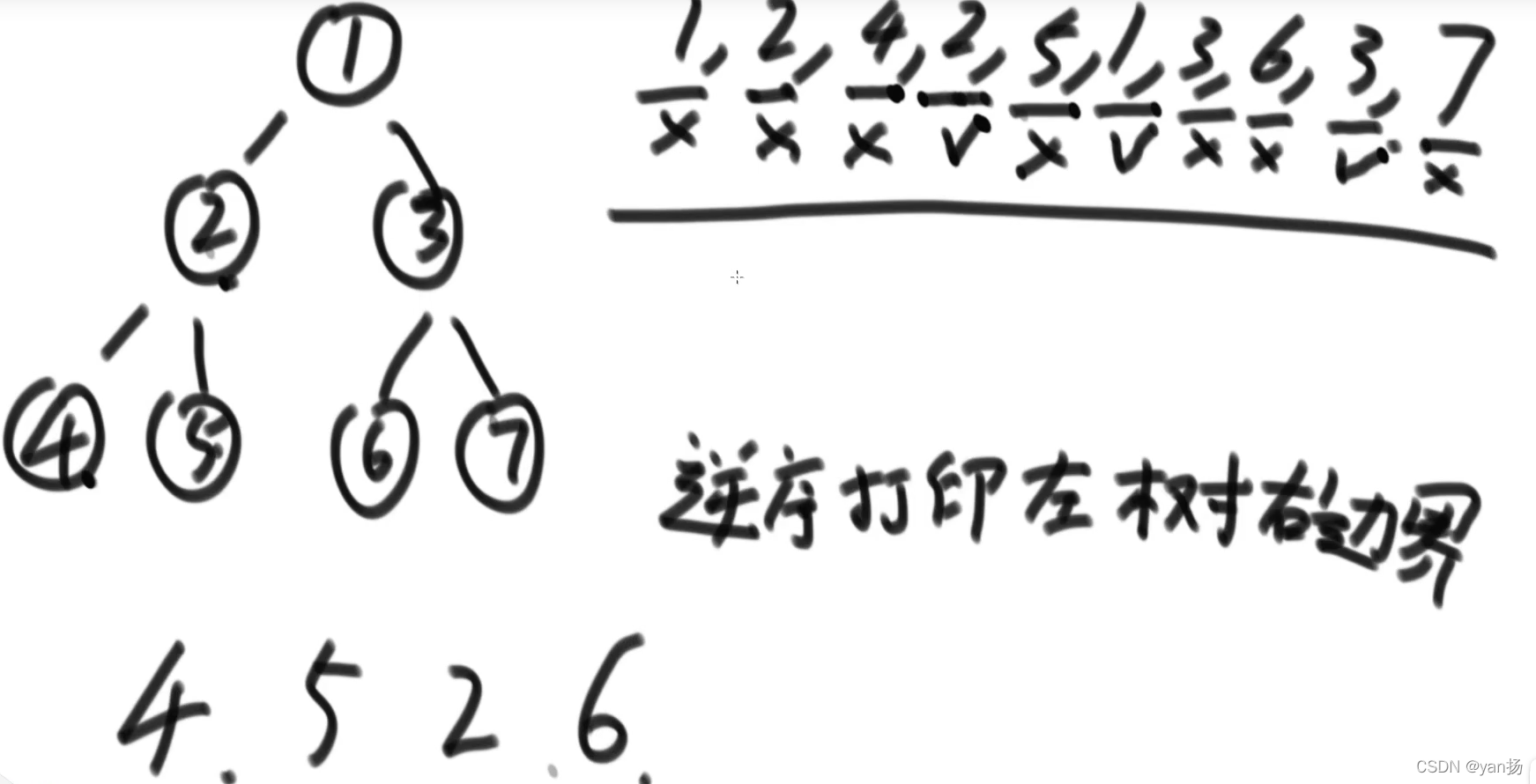
整个过程进行完之后,我们单独打印根节点的右边界:
7,3,1
所以总的顺序为:4,5,2,6,7,3,1
代码如下:
public class Solution {
List<Integer> list;
public List<Integer> postorderTraversal(TreeNode root) {
list=new ArrayList<>();
if (root==null){
return list;
}
TreeNode cur=root;
TreeNode mostRight=null;
while (cur!=null){
mostRight=cur.left;
if (mostRight!=null){
while (mostRight.right!=null&&mostRight.right!=cur){
mostRight=mostRight.right;
}
if (mostRight.right==null){
mostRight.right=cur;
cur=cur.left;
continue;
}else {
mostRight.right=null;
reverseAdd(cur.left);
}
}
cur=cur.right;
}
reverseAdd(root);
return list;
}
private void reverseAdd(TreeNode root){
TreeNode tail=reverse(root);
TreeNode cur=tail;
while (cur!=null){
list.add(cur.val);
cur=cur.right;
}
reverse(tail);
}
public TreeNode reverse(TreeNode root){
TreeNode cur=root;
TreeNode pre=null;
while (cur!=null){
TreeNode next=cur.right;
cur.right=pre;
pre=cur;
cur=next;
}
return pre;
}
}
三、二叉树的属性问题
1、对称二叉树
给定一颗二叉树,我们如何确定它是否镜像对称呢?
1)首先肯定要左子结点 等于 右子节点
2)左子节点的左结点 等于右子节点的右节点 并且 左子结点的右节点等于右子节点的左节点
代码如下:
public boolean isSymmetric(TreeNode root) {
if(root==null){
return true;
}
return dfs(root.left,root.right);
}
public boolean dfs(TreeNode left,TreeNode right){
if (left==null&&right==null){
return true;
}
if (left==null||right==null){
return false;
}
if (left==null||right==null){
return false;
}
return dfs(left.right,right.left)&&dfs(left.left,right.right);
}
2、二叉树的最大深度
二叉树的递归套路其实无非就是根结点向左右子树要信息的过程,因此我们思考,如何求根节点的最大深度呢?我们肯定要知道左子树的深度,右子树的深度,最大的深度再加上根节点就是题目的解了
当root==null时,我们的深度为0
代码如下:
public int maxDepth(TreeNode root) {
if(root==null) return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
事实上,这里我们是利用了dfs的思想 在之前我们说过层序遍历有每一层的信息,这个层信息不就是最大的深度吗 层序遍历求最大深度代码如下:
public int maxDepth(TreeNode root) {
if (root==null) return 0;
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
int res=0;//每遍历一层 res就加1
while (!queue.isEmpty()){
int size=queue.size();
for (int i=0;i<size;i++){
root=queue.poll();
if (root.left!=null) {
queue.offer(root.left);
}
if (root.right!=null){
queue.offer(root.right);
}
}
res++;
}
return res;
}
3、二叉树的最小深度
求最小深度时将Math.max换成Math.min即可,但要注意如果根节点的左或右子树为空的话是构不成子树的。而最小深度是要求从根节点到子树的。当左或右子树为空时,不符合要求。
class Solution {
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
// null节点不参与比较
if (root.left == null && root.right != null) {
return 1 + minDepth(root.right);
}
// null节点不参与比较
if (root.right == null && root.left != null) {
return 1 + minDepth(root.left);
}
return 1 + Math.min(minDepth(root.left), minDepth(root.right));
}
}
4、完全二叉树的结点个数
首先我们很容易想到的一种方式:递归调用 总的结点个数不就是 左子树结点+右子树结点+自己本身吗 因此我们很容易写出以下代码:
public int countNodes(TreeNode root) {
if (root==null) return 0;
return countNodes(root.left)+countNodes(root.right)+1;
}
但是,这样做我们完全没有利用到完全二叉树这个信息 完全二叉树的结点个数一定是有左结点才能有右节点的,所以如果我们采用层序遍历,一定优先有一个结点 只有左节点 或是叶子节点 因此我们计算当前这个结点是第几个结点就很容易算出总的结点个数:
public int countNodes(TreeNode root) {
if (root==null) return 0;
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
int num=1;
while (!queue.isEmpty()){
root=queue.poll();
if (root.left!=null&&root.right==null){
return num*2;
}
if (root.left==null&&root.right==null){
return num*2-1;
}
if (root.left!=null){
queue.offer(root.left);
}
if (root.right!=null){
queue.offer(root.right);
}
num++;
}
return -1;
}
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
public int countNodes(TreeNode root) {
//先求出 左右子树是不是等高的 如果等高左子树肯定是满二叉树
if (root==null){
return 0;
}
int leftHeight=getHeight(root.left);
int rightHeight=getHeight(root.right);
if (leftHeight==rightHeight){
return (1<<leftHeight)-1+1+countNodes(root.right);
}else {//左比右高 右必是满二叉树
return (1<<rightHeight)-1+1+countNodes(root.left);
}
}
public int getHeight(TreeNode root){
int res=0;
while (root!=null){
res++;
root=root.left;
}
return res;
}
5、平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
首先这道题我们很容易想到自顶而下的递归 判断根结点满不满足平衡树的定义 再递归查看左右子树是不是平衡树
public boolean isBalanced(TreeNode root) {
if (root==null) return true;
int left=height(root.left);
int right=height(root.right);
if (Math.abs(left-right)>1) return false;
return isBalanced(root.left)&&isBalanced(root.right);
}
private int height(TreeNode root) {
if (root==null) return 0;
return Math.max(height(root.left),height(root.right))+1;
}
但是这种自顶向下的递归 我们可能对下边的结点进行了多次遍历(由于要求深度)所以其实它的效率并不高,因此我们思考是否能自下而上 递归 只要子树是平衡树我们返回它的高度 不是平衡树 我们返回一个特殊值来标明它
class Solution {
public boolean isBalanced(TreeNode root) {
return recur(root) != -1;
}
private int recur(TreeNode root) {
if (root == null) return 0;
int left = recur(root.left);
if(left == -1) return -1;
int right = recur(root.right);
if(right == -1) return -1;
return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}
}
6、二叉树的所有路径
如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。
如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。
public List<String> binaryTreePaths(TreeNode root) {
//我们必须得有一个字符串来记录路径 并且得有一个List来存取字符串
List<String> res=new ArrayList<>();
dfs(root,"",res);
return res;
}
public void dfs(TreeNode root,String path,List res){
if (root.left==null&&root.right==null){//我们只有在子树不为空的时候才进行递归,因此root不会为空
path+=Integer.toString(root.val);
res.add(path);
}
path+=Integer.toString(root.val);
path+="->";
if (root.left!=null){
dfs(root.left,path,res);
}
if (root.right!=null){
dfs(root.right,path,res);
}
}
7、左叶子之和
一个节点为「左叶子」节点,当且仅当它是某个节点的左子节点,并且它是一个叶子结点。因此我们可以考虑对整棵树进行遍历,当我们遍历到节点 \textit{node}node 时,如果它的左子节点是一个叶子结点,那么就将它的左子节点的值累加计入答案。
public int res;
public int sumOfLeftLeaves(TreeNode root) {
if (root==null){
return 0;
}
res=0;
dfs(root);
return res;
}
private void dfs(TreeNode root) {
if (root==null){
return;
}
if (root.left!=null&&root.left.left==null&&root.left.right==null){
res+=root.left.val;
}
dfs(root.left);
dfs(root.right);
}
8、找树左下角的值
给定一个二叉树的 根节点
root
,请找出该二叉树的 **最底层 最左边 **节点的值。
看到这道题 大家是不是感觉巨容易 直接dfs一直找最左的直到没有左节点不就行了?
但是有一个问题 最左的不一定是最底层 因此我们可以尝试用层序遍历来做
public int findBottomLeftValue(TreeNode root) {
if (root==null){
return 0;
}
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
int size=queue.size();
for (int i=0;i<size;i++){
root=queue.poll();
if (root.right!=null){
queue.offer(root.right);
}
if (root.left!=null){
queue.offer(root.left);
}
}
}
return root.val;
}
其实这道题我们还是可以用递归来做,但注意这个最左的结点深度一定要是最大的
public int max_Value=0;
public int max_len=Integer.MIN_VALUE;
public int findBottomLeftValue(TreeNode root) {
dfs(root,0);
return max_Value;
}
private void dfs(TreeNode root, int level) {
if (root.left==null&&root.right==null){
if (level>max_len){
max_len=level;
max_Value=root.val;
}
return;
}
if (root.left!=null){
dfs(root.left,level+1);
}
if (root.right!=null){
dfs(root.right,level+1);
}
}
9、路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root==null){
return false;
}
if (root.left==null&&root.right==null){
return targetSum-root.val==0?true:false;
}
boolean left=root.left!=null?hasPathSum(root.left,targetSum-root.val):false;
boolean right=root.right!=null?hasPathSum(root.right,targetSum-root.val):false;
return left||right;
}
版权归原作者 yan扬 所有, 如有侵权,请联系我们删除。