【math系列】《深度学习》中主成分分析（PCA）的一个知识点证明

在Ian Goodfellow / Yoshua Bengios所著的《深度学习》第33页中：

$argmax [ tr(d^{T}X^{T}Xd)]\: \: \: \:\: \: \: \: \: s.t.\: \:\: d^{T}d = 1$

该公式中最优的d是 $X^{T}X$ 最大特征值对应的特征向量

** $argmax [ tr(d^{T}X^{T}Xd)]\: \: \: \:\: \: \: \: \: s.t.\: \:\: d^{T}d = 1$ **

证明：d是 $X^{T}X$ 最大特征值对应的特征向量

（我们在这里证明中的矩阵、向量的元素都是为实数，其中 ${\color{Red} X}$ 为n维方阵， ${\color{Red}d }$ 为n维列向量）

$\because\:(X^{T}X)^{T}=X^{T}X$

$\therefore \:\: X^{T}X$ 是实对称矩阵

那么存在一个正交矩阵Q，使得：

$Q^{-1}X^{T}XQ= diag(\lambda _{1},\lambda _{2},\lambda _{3}......\lambda _{n})=\Lambda$

令, $\lambda _{1}<\lambda _{2}<\lambda _{3}<......<\lambda _{n}$

其中 $Q=(q _{1},q _{2},q _{3}......q _{n})$ $q_{i}$ 为 $X^{T}X$ 的单位特征向量( $i=1,2,3,......n$ )

由于 $q_{i}$ 线性无关，则 $q _{1},q _{2},q _{3}......q _{n}$ 可线性表示任何n维向量

公式为： $a_{1}q_{1}+a _{2}q_{2}+a _{3}q_{3}+......+a _{n}q_{n}=d$ .............................................（1）

向量表示为： $(q _{1}\: q _{2}\: q _{3}\: ......\: q _{n})(a_{1}\: a _{2}\: a _{3}\: ......\: a _{n})^{T}=d$

令 $(a_{1}\: a _{2}\: a _{3}\: ......\: a _{n})^{T}=\alpha$

则公式（1）可以表示为： $Q\alpha =d$

$(Q\alpha) ^{T}X^{T}XQ\alpha=\alpha ^{T}(Q^{T}X^{T}XQ)\alpha=\alpha ^{T}(Q^{-1}X^{T}XQ)\alpha\: =\alpha ^{T}\Lambda \alpha$

将二次型 $\alpha ^{T}\Lambda \alpha$ 展开：

$\alpha ^{T}\Lambda \alpha=a_{1}^{2}\lambda _{1}+a_{2}^{2}\lambda _{2}+a_{3}^{2}\lambda _{3}+......+a_{n}^{2}\lambda _{n}\leq \lambda _{n}(a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+......+a_{n}^{2})$

又由约束条件： $d^{T}d = 1$

可得， $d^{T}d = (Q\alpha)^{T}Q\alpha=\alpha^{T}Q^{T}Q\alpha=\alpha^{T}\alpha=1$

则， $\alpha ^{T}\Lambda \alpha\leq \lambda_{n}(a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+......+a_{n}^{2}) =\lambda_{n}\alpha^{T}\alpha=\lambda_{n}$

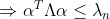
     ![\Rightarrow\alpha ^{T}\Lambda \alpha\leq \lambda_{n}](https://latex.codecogs.com/gif.latex?%5CRightarrow%5Calpha%20%5E%7BT%7D%5CLambda%20%5Calpha%5Cleq%20%5Clambda_%7Bn%7D)

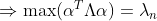
     ![\Rightarrow\max (\alpha ^{T}\Lambda \alpha)=\lambda_{n}](https://latex.codecogs.com/gif.latex?%5CRightarrow%5Cmax%20%28%5Calpha%20%5E%7BT%7D%5CLambda%20%5Calpha%29%3D%5Clambda_%7Bn%7D)

即取 $\alpha{}'=(0\: 0\: 0.......0\: 1 )^{T}$ 时， $\alpha {}'^{T}\Lambda {\alpha}'=\lambda_{n}$