插入排序和选择排序

目录

前言

排序中有着插入排序、选择排序、交换排序以及归并排序，而本次则只介绍前两种排序；而排序我全部码写成了升序，这一点需要注意！

1.排序

2.插入排序

将数据进行逐个比较，然后根据比较的结果大小从而进行插入，插入结束后，从而产生一个有序数列！

2.1直接插入排序

在了解到插入排序后，接下来看直接插入排序；顾名思义，当数据需要进行排序时，将该数据逐个比较，进行插入即可！

定义：

什么意思呢？

也就是先前说过的，假设前面i-1个数据有序，要将第i个数据进行插入，就需要与将其与前面数据进行比较即可；

下面给出一组数据的动态插入演示：

依据上述原理代码如下：

voidInsertSort(int* arr,int n){for(int i =0; i < n -1; i++){int end = i;int temp = arr[end +1];while(end >=0){if(arr[end]> temp){
                arr[end +1]= arr[end];--end;}else{break;}}
        arr[end +1]= temp;}}

分析：如果存在一些数据时乱序存在的，将这些数据进行插入排序；首先现将前两个数据进行比较，也就是起始时i=0，将arr[0]与arr[0+1]进行比较，如果前者比后者大，则将前者进行移动；重复这个过程就可以完成插入排序；

而根据上述现象，将end与end+1这两个位置进行比较，将arr[end+1]设置成temp，将end+1之前的数据与其比较，当temp比其前面数据大时不进行交换，否则将前面数据后移，然后再去比较end-1位置的数据；重复这个过程即可；最后将temp这个数据也就是end+1这个位置的数据进行插入即可！

特点：

2.2希尔排序(缩小增量排序)

希尔排序是直接插入排序的优化；将其效率大大提高了！

希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后重复上述分组和排序的工作。

也就是说，在之前的直接插入排序中，这种两个数之间的距离为1。现在需要开始时先设定其距离，这种距离需要进行调整改变，不断进行缩小这种距离。下面来看实例：

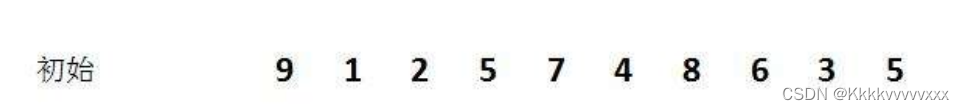
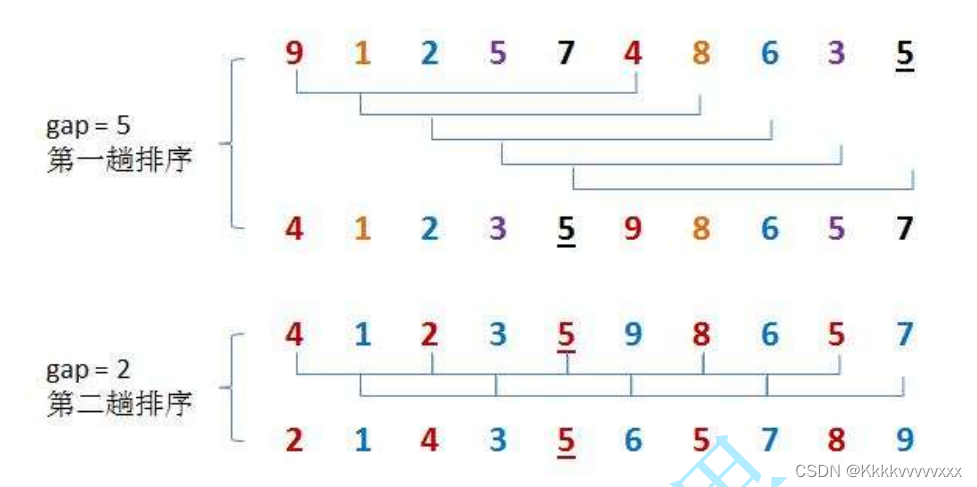
第一次距离为5，也就是说将两个距离为5的数进行比较，如果前者大于后者，则进行移动；第二次缩小这种距离变成2，将距离为2的数据在次进行比较移动即可。前面提到gap=1时就是直接插入排序，而这些gap不为1的排序统一被叫做预排序；其有一特点就是当gap越大时，数据挪动越快，gap越小时越接近于有序，这一点可以参考上图实例。

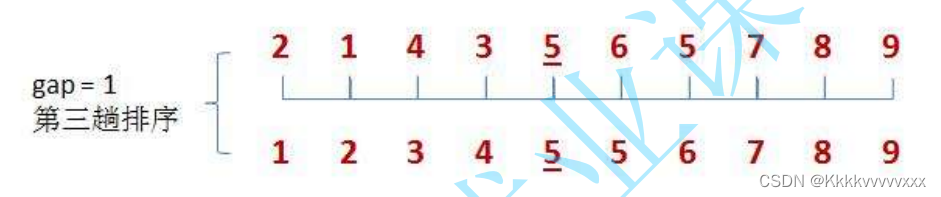
当gap=1时也就是直接插入排序!

voidShellSort(int* arr,int size){//缩小增量，分组依次进行比较int gap = size;while(gap >1){
        gap = gap /3+1;for(int i =0; i < size - gap; i++){int end = i;int temp = arr[end + gap];while(end >=0){if(arr[end]> temp){
                    arr[end + gap]= arr[end];
                    end -= gap;}else{break;}}
            arr[end + gap]= temp;}}}

分析：在上面的分析其实就是代码的各语句含义，首先先将gap=size，然后gap = gap / 3 + 1;从而保证了最后一次排序时它的gap一定是为1的；当然缩小gap也不是只有这一种办法，还可以gap=gap/2；这样最终gap也是为1的。

唯一需要注意的是，希尔排序是一组一组进行的，需要比较的两个数据之间的距离gap是变化缩小的，核心原理与直接插入排序一样，在此就不进行赘述了！

特点：

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就 会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比.

3.其时间复杂度是O(N^1.5)
4. 稳定性：不稳定

2.选择排序

基本思想：
每次从待排序的数据中选出最大或最小的元素，存放在队列的起始位置或者末尾位置，直至数据有序；

2.1直接选择排序

步骤：

• 在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
• 若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换
• 在剩余的array[i]–array[n-2]（array[i+1]–array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

voidSelectSort(int* arr,int n){int begin =0, end = n -1;while(begin <= end){int maxi = begin, mini = begin;for(int i = begin +1; i <= end;++i){if(arr[i]> arr[maxi]){
                maxi = i;}if(arr[i]< arr[mini]){
                mini = i;}}Swap(&arr[begin],&arr[mini]);//最大值在最前面需要特殊处理if(maxi == begin){
            maxi = mini;}Swap(&arr[end],&arr[maxi]);
        begin++;
        end--;}}

分析：在选择排序中对其进行了优化，同时寻找大数以及小数，将较大数存放在后边，较小数存放在前边即可！

特点：

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

相比于其他排序，无论一组数据是否有序又或者是接近于有序，选择排序都是时间复杂度都是O(N^2)，这一点也就导致了直接选择排序的效率十分低下！

2.2堆排序

堆排序其实在上一篇博客中我有写到，具体的原理在这就不分析了，可以转到上一篇博客进行查看：堆排序

升序：建大堆，进行交换调整
降序：建小堆，进行交换调整

//堆排序----(升序)voidSwap(int* p1,int* p2){int temp =*p1;*p1 =*p2;*p2 = temp;}voidAdjustHeapDown(int* arr,int parent,int size){int maxchild = parent *2+1;while(maxchild<size){if(arr[maxchild]< arr[maxchild +1]&& maxchild +1< size){
            maxchild++;}if(arr[parent]< arr[maxchild]){Swap(&arr[parent],&arr[maxchild]);//
            parent = maxchild;
            maxchild = parent *2+1;}else{break;}}}voidHeapSort(int* arr,int n){for(int i =(n -1-1)/2; i >=0;--i){AdjustHeapDown(arr, i, n);}for(int i =0; i < n; i++){Swap(&arr[0],&arr[n -1- i]);AdjustHeapDown(arr,0, n -1- i);}}

至于为什么向下调整，在这不过多介绍，降序的内容也在上一篇博客，请自行查看即可！

特点：

1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

Ending

关于插入排序和选择排序的内容也就到此为止了，其中比较难理解的就是希尔排序，这个需要去不断调试、测试才能更好地理解每一句的含义。堆排序的内容在上一篇花费了大量篇幅已经叙述完成，在本次也没有过多介绍。

就这样吧🙋‍♂️🙋‍♂️🙋‍♂️