聚类分析算法——层次聚类 详解

    层次聚类（Hierarchical Clustering）是一种无监督的机器学习方法，通过递归地对数据进行合并（或拆分），构建一个类似树的聚类结构，称为“树状图”（Dendrogram）。该算法通常用于探索数据的层次结构。根据聚类方向的不同，层次聚类可以分为“自底向上”（凝聚式聚类）和“自顶向下”（分裂式聚类）两种方法。

1. 基本概念

2. 凝聚层次聚类（Agglomerative Hierarchical Clustering）：- 这是自底向上的方法，最初将每个数据点视为单独的簇。- 在每一步，合并两个最相似的簇，直到所有数据点被合并为一个簇，或者达到预设的停止条件。- 常用于构建树状图，以观察数据聚类的逐层关系。

3. 分裂层次聚类（Divisive Hierarchical Clustering）：- 这是自顶向下的方法，最初将所有数据视为一个簇。- 然后递归地将簇分裂成两个较小的簇，直到每个簇只包含一个数据点或达到预设的停止条件。- 虽然分裂式方法可以生成类似的层次结构，但在实际中应用较少，因为计算复杂度较高。

2. 层次聚类的底层原理

2.1 树状图（Dendrogram）

    树状图是一种分层结构的图形，描述了在不同的相似度或距离阈值下数据被合并成簇的过程。图中每一层的分支表示簇的合并过程，通过设定不同的阈值可以观察不同层次的聚类结果。

2.2 距离度量

层次聚类的核心是如何定义簇之间的相似性（或距离）。常用的距离度量包括：

1. 欧氏距离（Euclidean Distance）：- 用于衡量两个点之间的直线距离，适用于数值型数据。- 距离公式为：
2. 曼哈顿距离（Manhattan Distance）：- 度量每个坐标轴的绝对距离之和，适合某些具有特定物理意义的数据。- 公式为：
3. 皮尔逊相关系数（Pearson Correlation）：- 衡量两个变量间的线性相关性，适用于观测数据或时间序列数据。
4. 余弦相似度（Cosine Similarity）：- 用于文本数据和高维稀疏数据，通过余弦值衡量向量间的角度相似性。

2.3 聚类链接方式

不同链接方式对簇的相似性有不同的定义，以下是几种主要链接方式：

1. 单链接（Single Linkage）：- 定义两个簇之间的最小距离，即最近的两个样本点之间的距离。- 优点是计算简单，缺点是容易出现“链状效应”，导致簇间结构不明确。
2. 完全链接（Complete Linkage）：- 定义两个簇之间的最大距离，即最远的两个样本点之间的距离。- 通常生成相对紧密的簇，但可能导致簇形状不自然。
3. 平均链接（Average Linkage）：- 计算簇内所有点对之间的平均距离，适合生成平均紧密的簇。- 缺点是计算复杂度较高。
4. 质心链接（Centroid Linkage）：- 计算簇的质心，并用两个簇的质心之间的距离来衡量相似度。- 适合均值点分布较均匀的数据，但如果聚类结果为非凸形状，效果较差。

2.4. 聚类间距离的计算方法

合并簇时需要定义簇与簇之间的距离，不同的距离定义方式会导致聚类结果不同。常用的几种计算方式有：

1. 单链（Single Linkage）： 两个簇中最小距离的数据点之间的距离，即最近邻距离。适合发现细长或不规则形状的簇，但可能导致链式效果。
2. 全链（Complete Linkage）： 两个簇中最大距离的数据点之间的距离，即最远邻距离。倾向于生成较紧凑的簇，适合球形分布，但可能忽略簇的全局形状。
3. 平均距离（Average Linkage）： 两个簇中所有点对之间的平均距离，常用于减少单链和全链方法的极端情况。
4. 质心距离（Centroid Linkage）： 计算两个簇质心之间的距离，即簇中所有点的平均位置。其中 ​ 和 ​ 分别是簇 A 和簇 B 的质心。

3. 层次聚类的算法步骤（凝聚层次聚类）

以下是凝聚层次聚类的详细步骤：

1. 计算初始距离矩阵： 计算数据集中每两个点之间的距离，将距离存入矩阵中。常用的距离度量是欧氏距离。
2. 初始化每个点为一个单独的簇： 初始时，每个数据点都视为一个独立的簇。
3. 合并最近的簇： 查找距离矩阵中距离最近的两个簇，合并这两个簇，并更新簇之间的距离。
4. 更新距离矩阵： 更新新的簇与其他簇之间的距离。不同的簇间距离计算方式会影响聚类结果，常用的计算方式包括单链（最小距离）、全链（最大距离）、平均距离和质心距离。
5. 重复步骤 3 和 4，直到所有点合并成一个簇或达到预设的聚类数。

树状图的生成

在合并簇的过程中，记录每次合并的簇对及其距离，即可构建一个树状图（dendrogram），展示数据集在不同距离阈值下的聚类结构。

4. 层次聚类的Python实现示例

    层次聚类可以使用 

scipy

和

scikit-learn

等库来实现。

    层次聚类的时间复杂度较高，通常为 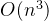![O(n^{3})](https://latex.csdn.net/eq?O%28n%5E%7B3%7D%29)，其中 n 是数据点的数量。其高复杂度源于每次合并操作后都要更新距离矩阵。因此，层次聚类通常适合小规模数据集。

以下先给出伪代码，之后是基于

scipy.cluster.hierarchy

模块和

sklearn

的两种实现。

4.1 层次聚类的伪代码

HierarchicalClustering(X):
    1. 计算初始距离矩阵，设每个点为独立簇
    2. 重复以下步骤直到簇数等于 1：
        a. 查找距离矩阵中距离最近的两个簇 (A, B)
        b. 合并簇 A 和 B，形成新簇 C
        c. 更新距离矩阵：根据选定的距离方式，计算新簇 C 与其他簇的距离
    3. 构建树状图，并返回层次聚类结构

4.2 使用

scipy

实现层次聚类并绘制树状图

import numpy as np
from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt

# 生成一些二维数据点
np.random.seed(42)
X = np.random.randn(20, 2)

# 使用scipy的linkage函数进行凝聚层次聚类
# 使用欧氏距离和单链接
Z = linkage(X, method='single', metric='euclidean')

# 绘制树状图
plt.figure(figsize=(10, 6))
dendrogram(Z, labels=range(1, 21))
plt.title("Dendrogram for Hierarchical Clustering")
plt.xlabel("Sample index")
plt.ylabel("Distance")
plt.show()

在上述代码中：

• linkage函数用于执行凝聚层次聚类。method参数指定了链接方式，metric参数指定了距离度量方式。
• dendrogram函数生成树状图，展示每次合并的过程。

linkage

函数的

method

参数可以设置成不同的链接方法，例如

single

（单链）、

complete

（全链）、

average

（平均）、

ward

（方差最小法）。

4.3 使用

scikit-learn

实现层次聚类并生成聚类标签

from sklearn.cluster import AgglomerativeClustering

# 定义层次聚类模型
model = AgglomerativeClustering(n_clusters=2, linkage='ward')

# 训练模型并获取聚类标签
labels = model.fit_predict(X)
print("Cluster labels:", labels)

在

AgglomerativeClustering

中：

• n_clusters 参数设定要生成的簇数。
• linkage 参数可以设置链接方法。

4.4 层次聚类的改进方法

为了降低层次聚类的复杂度，可以考虑以下改进方法：

1. BIRCH（Balanced Iterative Reducing and Clustering using Hierarchies）： BIRCH 通过创建一个聚类特征树（Clustering Feature Tree, CF Tree）来对大规模数据进行分层处理。它可以通过逐层构建特征树来降低聚类复杂度，是一种适合大数据的层次聚类算法。
2. OPTICS（Ordering Points To Identify the Clustering Structure）： OPTICS 改进了层次聚类在非凸簇上的表现，能够处理不同密度的簇。它按数据点的密度生成数据的分层顺序，在树状图上根据密度划分不同簇。
3. 通过聚类数据抽样减少复杂度： 对于大规模数据集，可以使用数据抽样的方法降低数据规模，进行层次聚类分析后将结果再映射回完整数据上，以此减小计算开销。

5. 源代码解析

在底层实现中，

linkage

函数的核心步骤如下：

1. 初始化簇：开始时将每个点视为单独的簇。
2. 计算距离：将距离矩阵存储为下三角矩阵，以节省空间和提高效率。
3. 合并最小距离簇：在每一轮迭代中查找距离矩阵中最小值，合并对应的两个簇。
4. 更新距离矩阵：根据所选的链接方式，更新新簇与所有其他簇的距离。
5. 重复步骤3和4，直到只有一个簇或达到预设停止条件。

6. 层次聚类的优缺点

优点

1. 无需预先指定簇数：层次聚类在生成树状图（dendrogram）后，可以按需选择不同的层次切割位置，从而得到不同数量的簇。
2. 适用于不同规模的簇：层次聚类可以适用于不规则形状的簇，尤其是在选择单链或平均距离时。
3. 层次性：层次聚类提供了数据的层次结构，使得不同粒度的聚类信息都能展现，适合可视化。
4. 可解释性：通过树状图直观展示聚类过程和结构，便于解释数据点之间的层次关系。

缺点

1. 计算复杂度高：层次聚类的时间复杂度通常为 ，在大数据集上计算代价很高，通常只适合较小的数据集。
2. 难以调整合并错误：一旦在某一层次上错误地合并了两个簇，这个错误会一直影响后续层次，无法在后续步骤中调整。
3. 对噪声和离群点敏感：层次聚类在没有噪声过滤的情况下，可能会将离群点视为一个单独的簇或加入其他簇，从而影响聚类质量。
4. 不同链接方法的局限性：不同的链接方法（单链、全链等）对聚类结果影响较大，且可能导致链式聚类等问题，选择合适的方法需要根据数据特性调整。

7. 层次聚类的应用

• 生物学：用于基因表达数据聚类、谱系分析。
• 文本处理：文本分类，生成相似度树状结构。
• 市场分析：将客户按购买行为进行分层，以便于开展不同层次的营销策略。

层次聚类算法为数据分析提供了逐层揭示模式的能力，有助于理解和挖掘数据的内在结构。