
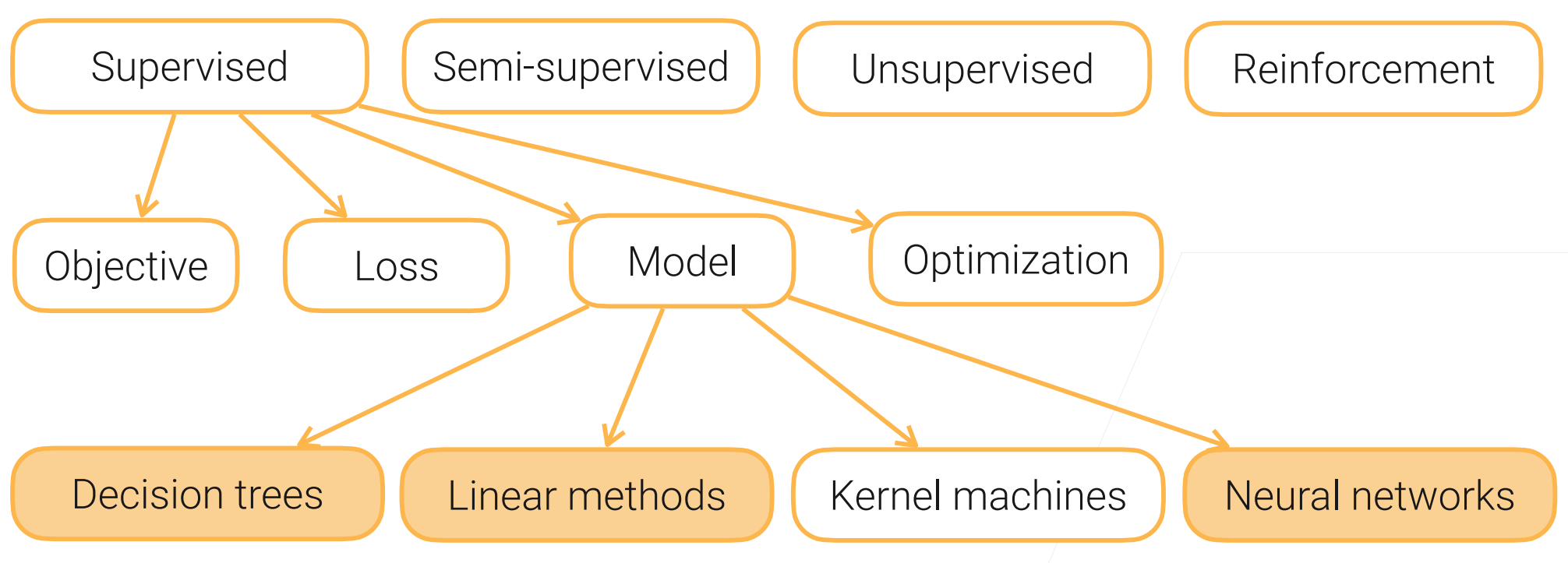
一、决策树
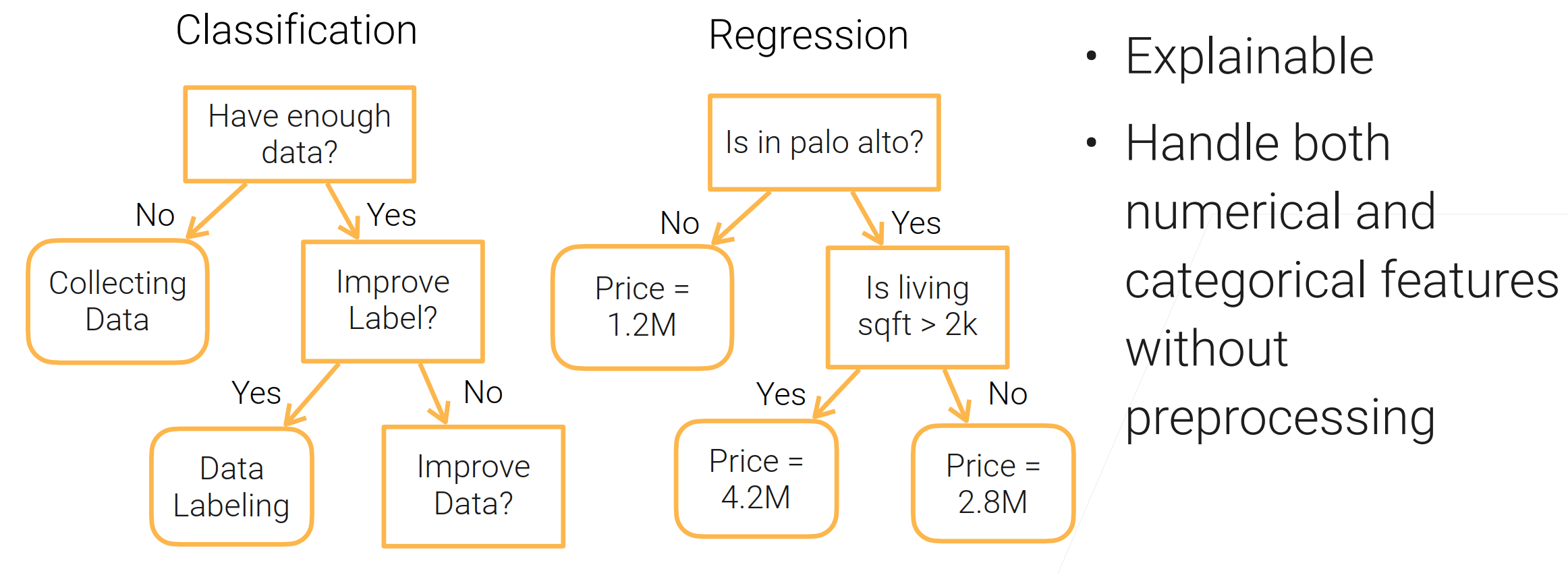
决策树(decision tree):是一种基本的分类与回归方法,此处主要讨论分类的决策树。
在分类问题中,表示基于特征对实例进行分类的过程,可以认为是if-then的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
决策树通常有三个步骤:特征选择、决策树的生成、决策树的修剪。
用决策树分类:从根节点开始,对实例的某一特征进行测试,根据测试结果将实例分配到其子节点,此时每个子节点对应着该特征的一个取值,如此递归的对实例进行测试并分配,直到到达叶节点,最后将实例分到叶节点的类中。
好处:
- 可以解释(可以让人看到对数据处理的过程)【常用于银行业保险业】;
- 可以处理数值类和类别类的特征;
坏处:
- 不稳定(数据产生一定的噪音之后,整棵树构建出的样子可能会不一样)【使用集成学习 (ensemble learning)可以解决】
- 数据过于复杂会生成过于复杂的树,会导致过拟合【把决策树的枝剪掉一些(在训练时觉得太复杂了就停下来,或在训练之后把特往下的节点给剪掉)】
- 大量的判断语句(太顺序化),不太好并行【在性能上会吃亏】
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分,也对应着决策树的构建。
- 1) 开始:构建根节点,将所有训练数据都放在根节点,选择一个最优特征,按着这一特征将训练数据集分割成子集,使得各个子集有一个在当前条件下最好的分类。
- 2) 如果这些子集已经能够被基本正确分类,那么构建叶节点,并将这些子集分到所对应的叶节点去。
- 3)如果还有子集不能够被正确的分类,那么就对这些子集选择新的最优特征,继续对其进行分割,构建相应的节点,如果递归进行,直至所有训练数据子集被基本正确的分类,或者没有合适的特征为止。
- 4)每个子集都被分到叶节点上,即都有了明确的类,这样就生成了一颗决策树。
**随机森林——让决策树稳定的方法 **
- 训练多个决策树来提升稳定性:
- 每棵树会独立的进行训练,训练之后这些树一起作用得出结果;
- 分类的话,可以用投票(少数服从多数);
- 回归的话,实数值可以时每棵树的结果求平均;
- 随机来自以下两种情况:
- Bagging:在训练集中随机采样一些样本出来(放回,可重复);
- 在bagging出来的数字中,再随机采样一些特征出来,不用整个特征;
Boosting——另一个提升树模型的方法
- 顺序完成多个树的训练(之前是独立的完成)
- 例子说的是,利用训练好的树与真实值做残差来训练新的树,训练好了之后再与之前的树相加
- 残差 等价于 取了一个平均均方误差(预测值与真实值的)再求梯度乘上个负号
总结:
- 树模型在工业界用的比较多【简单,训练算法简单,没有太多的超参数,结果还不错】(不用调参结果还不错)
- 树模型能够用的时候,通常是第一选择。
二、线性模型
以之前房价预测的例子: 在模型中的参数w(权重)与b(偏差)是可以通过数据学习的
 线性回归预测的方程:
线性回归预测的方程:
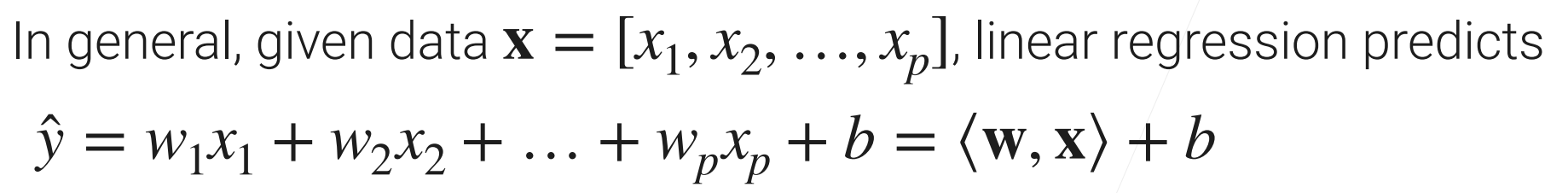 ** 目标函数**(优化 平均均方误差 MSE)
** 目标函数**(优化 平均均方误差 MSE)
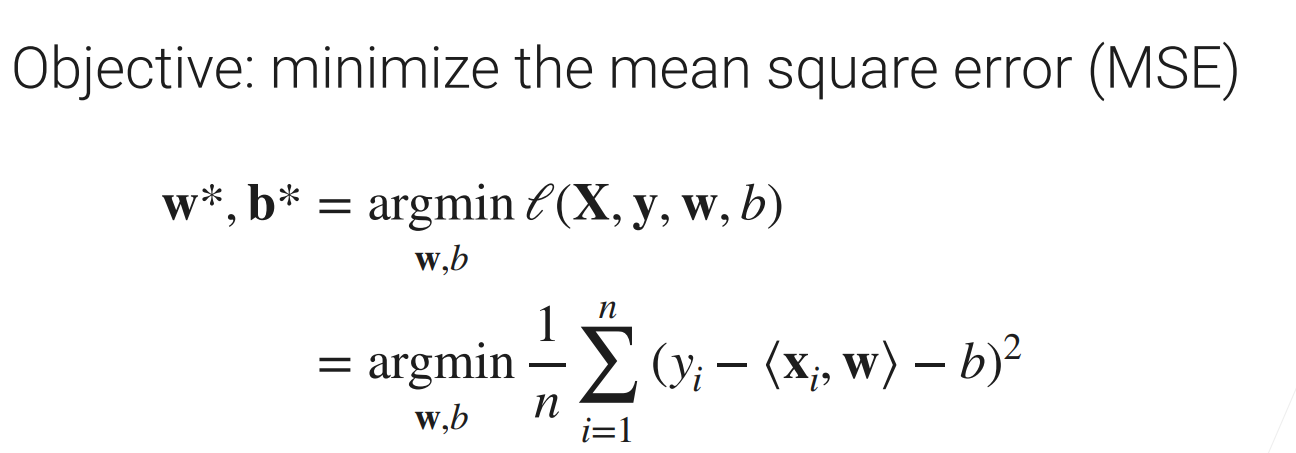
- 回归的输出是一段连续的实数,而分类是输出对样本类别的预测;
- 在这个部分,我们所关心的是多类的分类问题
- 可以使用向量来输出(不是输出1个元素而是m个元素 m为类别数);
- 使用线性模型预测出样本数据类别的置信度,最大置信度的类别为样本数据所对于的类别并用onehot(独热)编码输出。
- 这里的目标函数是**MSE(均方误差) **
使用MSE做为目标函数的分类存在问题
使用均方误差(MSE)作为目标函数,使得预测值趋近真实值,但是作为分类关心的是数据对应类别的置信度。
解决方法:
- 让模型更加专注到把正确的类别弄出来;
- 具体来说:把预测的分数换成概率的形式(Softmax函数);
- 衡量真实值概率与预测值概率的区别,用Cross-entropy(交叉熵) 。
总结
- 线性模型是一个形式简单、易于建模的机器学习模型,因为w直观表达了各属性在预测中的重要性,因此线性模型有很好的可解释性。
- 线性回归背后的逻辑是用模型的预测值去逼近真实标记y,并通过计算训练样本在向量空间上距离模型线的欧式距离之和的最小值来确定参数w和b。
- 线性回归可写成广义线性模型形式:g(y) = wx + b,通过选择不同的联系函数 g(.)会构成不同的线性回归模型。
- 在遇到多分类学习任务时,基本的解决思路是“拆解法”,即将多分类任务拆为若干个二分类任务求解。
- 当不同类别的样例数不同时,会造成类别不平衡问题,解决该问题的基本策略是对数据进行“再缩放。
三、随机梯度下降
我们要求解,一般是可以通过显式解来求的,一般使用随机梯度下降的方法(SGD)
随机梯度下降(SGD)是一种简单但非常有效的方法,多用用于支持向量机、逻辑回归(LR)等凸损失函数下的线性分类器的学习。并且SGD已成功应用于文本分类和自然语言处理中经常遇到的大规模和稀疏机器学习问题。
SGD既可以用于分类计算,也可以用于回归计算。
SGD算法是从样本中随机抽出一组,训练后按梯度更新一次,然后再抽取一组,再更新一次,在样本量及其大的情况下,可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。(重点:每次迭代使用一组样本。)
为什么叫随机梯度下降算法呢?这里的随机是指每次迭代过程中,样本都要被随机打乱,这个也很容易理解,打乱是有效减小样本之间造成的参数更新抵消问题。
小批量随机梯度下降(Mini-batch SGD)
小批量随机梯度下降,是整个机器学习里面,目前来说几乎是唯一的求解方法,虽然线性模型有很多的方法来求解,但是小批量随机梯度下降可以解决出决策树以外的模型。
- w 是模型的参数,包括线性模型的w(权重)和b(偏移)
- b 表示批量大小【需要自己设计,老师的动手学深度学习的课程里面有讲怎么选】
- η 表示在时间 t 的学习率【需要我们来设计,不能选太小,会走不动;也不能选太大,可能整个模型就出问题了】
 步骤:
步骤:
- 时刻1时随机的取一个 w1 ;
- 持续时间到模型收敛(发现目标函数在每个样本平均的损失不再下降;或者是其他的指标基本上趋向平衡)
- 在每一步里,在所有的样本中随机采样1个 It 出来,It 的大小是等于 b 的
- 把 It 当成是当前的训练样本 去算目标函数,再通过这个损失函数进一步求得 下一步得权重
- 不断重复上面的两点直至收敛
优点:小批量随机梯度下降可以解决出决策树以外的模型
缺点:超参数b与η需要自己选
**实现随机梯度下降 **
def SGD_LR(data_x, data_y, alpha=0.1, maxepochs=10000,epsilon=1e-4):
xMat = np.mat(data_x)
yMat = np.mat(data_y)
m, n = xMat.shape
weights = np.ones((n, 1)) # 模型参数
epochs_count = 0
loss_list = []
epochs_list = []
while epochs_count < maxepochs:
rand_i = np.random.randint(m) # 随机取一个样本
loss = cost(xMat,weights,yMat) #前一次迭代的损失值
hypothesis = sigmoid(np.dot(xMat[rand_i,:],weights)) #预测值
error = hypothesis -yMat[rand_i,:] #预测值与实际值误差
grad = np.dot(xMat[rand_i,:].T,error) #损失函数的梯度
weights = weights - alpha*grad #参数更新
loss_new = cost(xMat,weights,yMat)#当前迭代的损失值
print(loss_new)
if abs(loss_new-loss)<epsilon:
break
loss_list.append(loss_new)
epochs_list.append(epochs_count)
epochs_count += 1
print('迭代到第{}次,结束迭代!'.format(epochs_count))
plt.plot(epochs_list,loss_list)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
return weights
优点:
- (1)由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数据 上的损失函数,这样每一轮参数的更新速度大大加快。
缺点:
- (1)准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
- (2)可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
- (3)不易于并行实现。
版权归原作者 Lingxw_w 所有, 如有侵权,请联系我们删除。