冰冰学习笔记：一步一步带你实现《栈和队列》

欢迎各位大佬光临本文章！！！

还请各位大佬提出宝贵的意见，如发现文章错误请联系冰冰，冰冰一定会虚心接受，及时改正。

本系列文章为冰冰学习编程的学习笔记，如果对您也有帮助，还请各位大佬、帅哥、美女点点支持，您的每一分关心都是我坚持的动力。

我的博客地址：bingbing~bang的博客_CSDN博客https://blog.csdn.net/bingbing_bang?type=blog

我的gitee：冰冰棒 (bingbingsupercool) - Gitee.comhttps://gitee.com/bingbingsurercool

系列文章推荐

冰冰学习笔记：一步一步带你实现《顺序表》

冰冰学习笔记：一步一步带你实现《单链表》

冰冰学习笔记：一步一步带你实现《双向带头循环链表》

前言

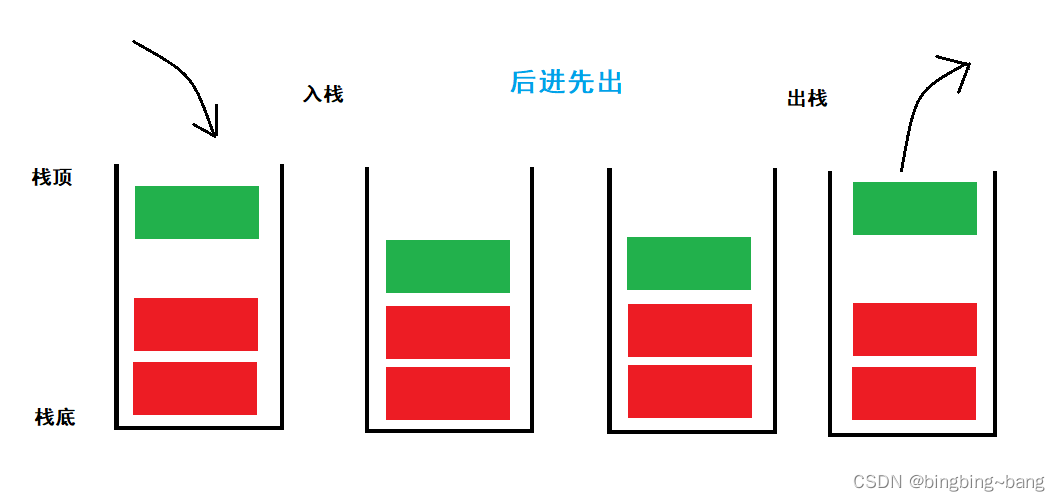
    **栈**和队列也是数据结构中的一种，二者都可以使用链表或者顺序表实现。对于栈来说，其最大的特点就是数据**先入后出**，每一个栈都有栈顶和栈底，数据总是放入栈顶，也总是从栈顶拿出。基于这些特点，实现栈最好的方式是使用顺序表，因为我们仅对顺序表进行尾插尾删就可实现栈。

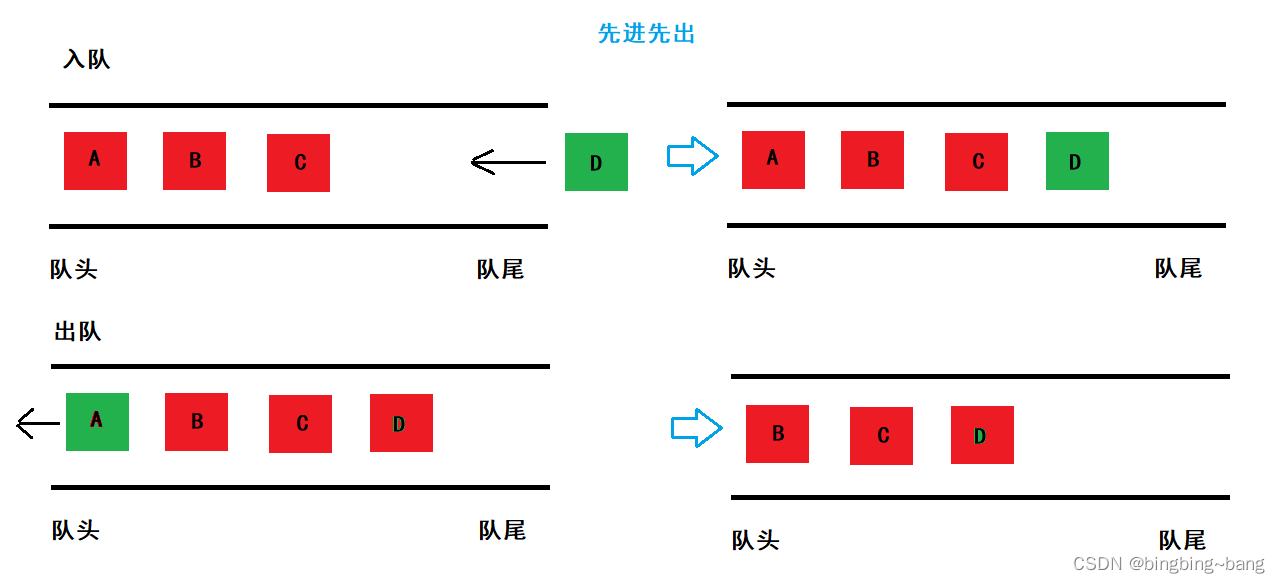
    **队列**也是一种特殊的线性表。队列的特点是数据遵循**先入先出**的原则，每个队列都有对头和队尾，数据总是从对尾进入，从队头拿出。相比于栈，队列则更适合使用链表，因为队列在对头出数据更加方便，顺序表需要移动数据，效率太低。

    下面我们开始介绍栈与队列的具体实现方式。

一、栈的实现

    栈，归根结底只是一种特殊的线性表，前面的文章中我们具体介绍了线性表中顺序表的实现方式，因此栈的实现对于我们来说小菜一碟。栈通常的接口含有初始化，入栈，出栈，获取栈顶元素，判断栈是否为空，计算栈的元素个数，栈销毁。

1.1结构创建与初始化函数

    如前文所讲，栈的本质还是顺序表，因此栈的结构中应该包含三个元素：栈的存储数据类型、栈顶元素下标，存储空间大小。

    对于初始化函数，我们也可以一开始就为存储元素的空间开辟一部分，也可以在空间扩容时增加。这里采取的是后面统一扩容的方式，因此初始化函数只需要将top与capacity进行归零操作，然后将a赋值为空指针。

函数代码：

void StackInit(ST* ps)
{ 
    assert(ps);
    ps->capacity = ps->top = 0;
    ps->a = NULL;
}

1.2入栈函数

    入栈操作是将数据从栈顶放入，由于我们实现的方式是顺序表，因此我们可以将数组开头视为栈底，数组结尾视为栈顶。因此数据入栈即为将数据插入到数组尾部，也就是顺序表的尾插操作。

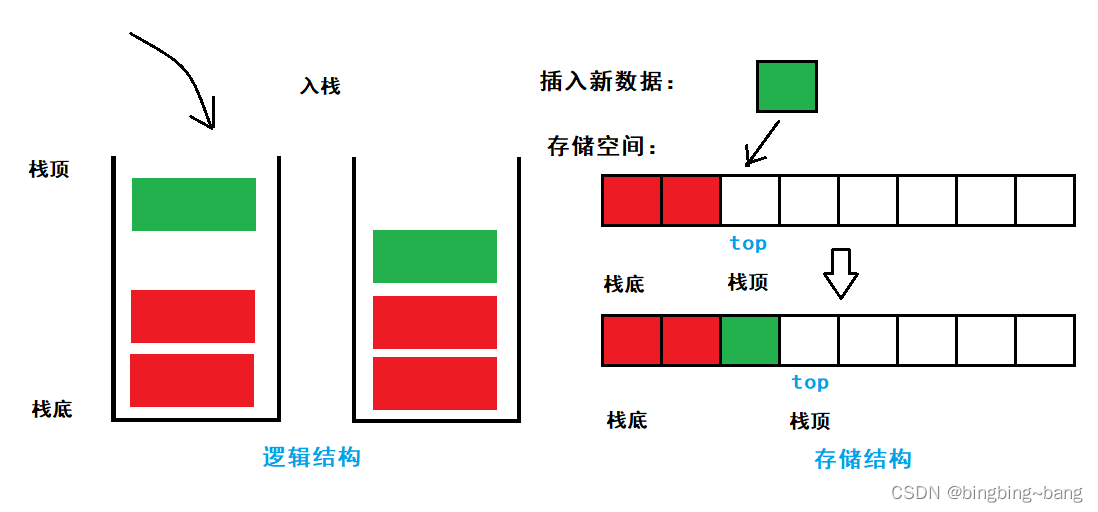
    这样一分析，我们的思路就清晰了。插入函数进来一定要先判断原有空间是否充足，能够存储数据，如果不能需要先开辟空间然后将数据存储进去。空间开辟完成后，将插入数据放入到顺序表尾部，也就是栈顶指向的位置，然后更新栈顶top指向的位置。

函数代码：

void StackPush(ST* ps, STDataType x)
{
    assert(ps);
    if ( ps->capacity == ps->top )
    {
        int newsize = ps->capacity==0?4:2*ps->capacity;
        STDataType* tmp = (STDataType*)realloc(ps->a,newsize*sizeof(STDataType));
        if ( tmp == NULL )
        {
            perror("StackPush::realloc");
            exit(-1);
        }
        ps->a = tmp;
        ps->capacity = newsize;
    }
    ps->a[ps->top] = x;
    ps->top++;
}

1.3出栈函数

    由于栈必须满足栈空间的数据从栈顶取出，因此，出栈函数就意味着删除栈顶的元素，及顺序表中数组尾部的元素，也就是尾删。

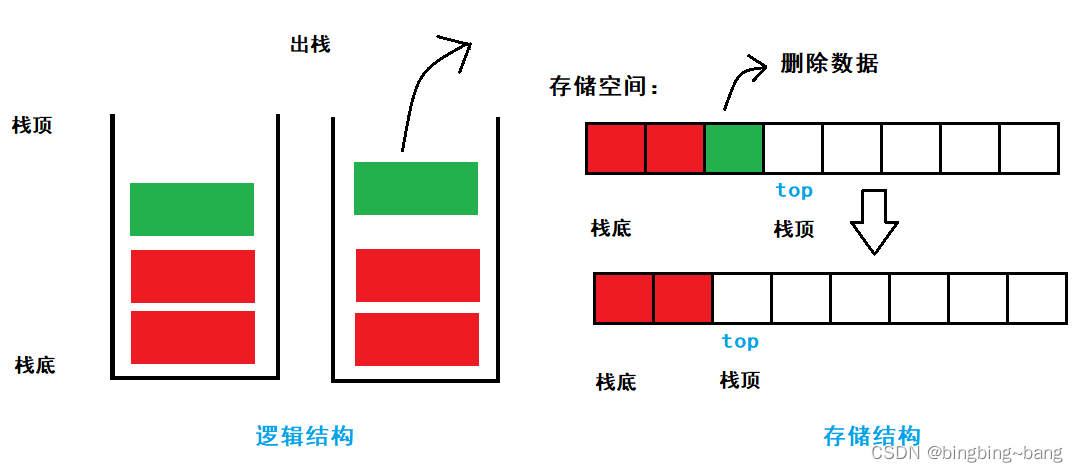
    实际操作中我们并不需要真正的将内存空间释放，我们只需要将top向后移动即可，这样顺序表访问不到元栈顶的数据，即为删除。**注意**：此处调用了判空函数，因为只有当栈中含有元素的时候才能正确执行删除数据功能，栈为空，数据无法删除，应直接报错。

函数代码：

void StackPop(ST* ps)
{
    assert(ps);
    assert(!StackEmpty(ps));
    ps->top--;
}

1.4获取栈顶元素

    获取栈顶元素函数与出栈函数不同。出栈函数是将栈空间中栈顶的元素弹出，也就是删除销毁，获取栈顶函数是将栈顶空间保存的数据取出，并不会改变栈空间的数据存储。因此我们只需要将顺序表中top所指向的上一个空间的位置存储的数据返回即可。

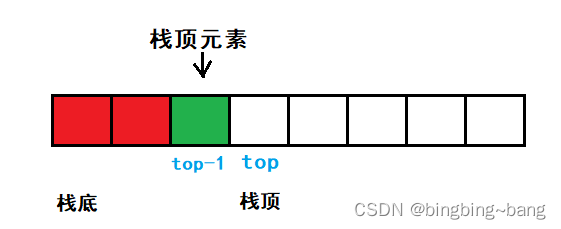
函数代码：

STDataType StackTop(ST* ps)
{
    assert(ps);
    assert(!StackEmpty(ps));
    return ps->a[ps->top-1];
}

1.5判断栈是否为空

    我们在判断栈是否为空的函数时使用了布尔类型，如果栈为空则返回true，不是空则返回false。使用布尔类型，我们得先包含头文件<stdbool.h>，这样C语言才能识别布尔类型。

    我们可以使用top来确定栈空间是否为空，若栈为空，则top必定为0。使用if语句进行判断可以，但是不够简洁，我们完全可以直接返回top==0，如果满足即为真，不满足即为假。

函数代码：

bool StackEmpty(ST* ps)
{
    assert(ps);
    return ps->top == 0;
}

1.6计算栈空间与栈销毁

    计算栈空间元素个数的函数比较简单，由于栈是顺序表结构实现的，因此栈顶下标top的大小即为栈空间的元素个数，直接返回即可。

    栈销毁函数就是将开辟的空间进行释放，与顺序表的释放函数一致。

函数代码：

//栈销毁
void StackDestroy(ST* ps)
{
    assert(ps);
    free(ps->a);
    ps->a = NULL;
    ps->capacity = ps->top = 0;
}

//计算栈空间元素个数
STDataType StackSize(ST* ps)
{
    assert(ps);
    return ps->top;
}

二、队列的实现

    队列的性质和栈恰恰相反，队列采用先进先出的原则，插入数据的一端称为队尾，拿出数据的一端称为队头，队列的代码实现中通常包含队列初始化、入队、出队、获取队头元素、获取队尾元素、队列判空、队列元素个数获取、队列销毁。

2.1队列结构创建与初始化函数

    队列的搭建可以采用顺序表或者链表，由于队列需要使用尾增与头删，所以顺序表实现并不划算，原因在于顺序表进行头删的时候，元素需要移动，增加了时间复杂度。在这里我们采用的是链表的结构。

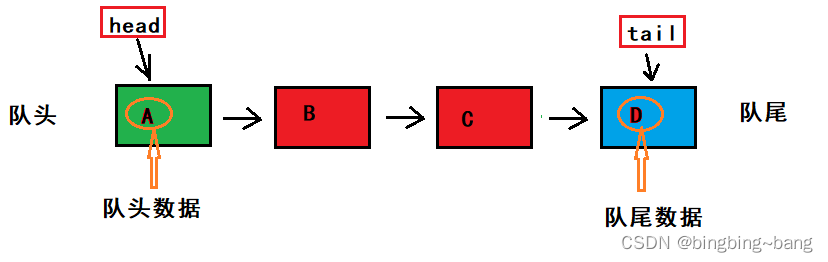
    如图所示，队列的结点中还是和单链表一致，含有存储元素data，以及指向下一个结点的指针next。但是队列结构中含有两个指针，分别为头指针head、尾指针tail，以及一个保存队列元素个数的size变量。head指针指向队列的头，尾指针记录队列的尾，这样数据插入的时候就不用遍历链表找尾部，直接连接在记录尾部的指针tail中。单链表中我们并没有采用此种方式，原因在于队列的性质规定，队列只能从尾部进行数据插入，为了方便可以采用这种情况。但是，单链表中数据插入的方式不仅尾插一种，任意位置的插入还需要遍历寻找指针，此种方式虽能解决尾插，但是意义不大，其他算法还是O(N)。

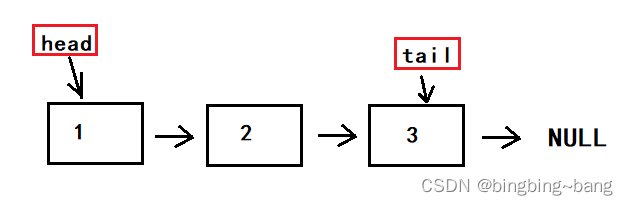
    队列的初始化函数与单链表相似，初始化时不需要开辟头结点（开辟也可以），只需要将head指针与tail指针指向NULL，size的大小变为0。

函数代码：

//队列初始化
void QueueInit(Queue* pq)
{
    assert(pq);
    pq->head = pq->tail = NULL;
    pq->size = 0;
}

2.2入队列函数

    入队列函数本质就是单链表的尾插函数，因为我们队列结构体中包含了记录尾指针的tail指针，因此我们不需要遍历寻找尾指针，直接将新开辟的结点newnode连接到尾指针tail后面即可。队列结构中含有记录元素个数的数据size，因此插入结点后应该将size进行自增。

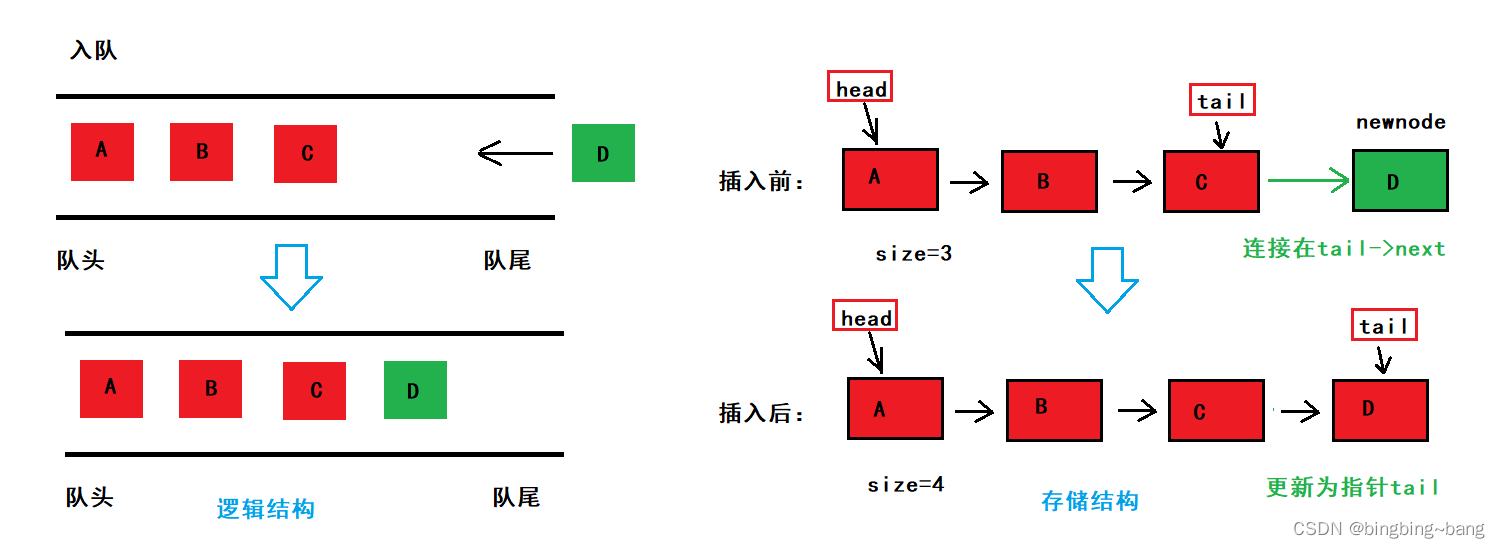注意，由于我们并没有开辟头结点，所以我们需要判断是否为第一次的数据插入，如果是第一次插入数据，tail和head为空，无法将数据直接连接在tail后方，因此需要将数据直接连接在head后面。

函数代码：

void QueuePush(Queue* pq, QueueDataType x)
{
    assert(pq);
    QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
    if ( newnode == NULL )
    {
        perror("QueuePush::malloc");
        exit(-1);
    }
    newnode->Data = x;
    newnode->next = NULL;
    //第一次插入
    if (pq->tail == NULL )
    {
        pq->head = pq->tail = newnode;
    }
    //其他情况
    else
    {
        pq->tail->next = newnode;
        pq->tail = newnode;
    }
    pq->size++;//元素个数自增
}

2.3出队列函数

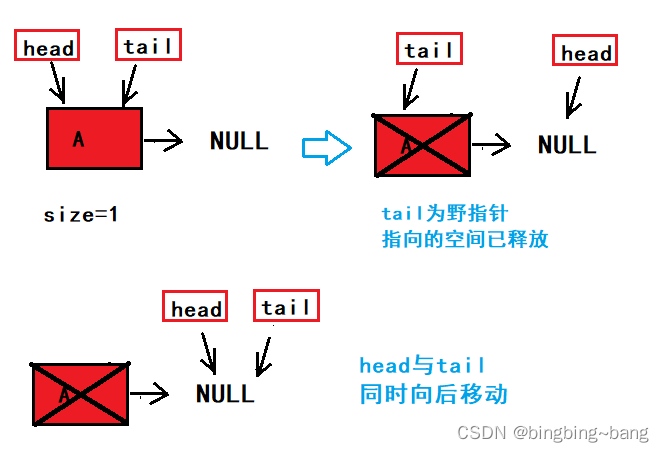
    队列的性质决定了实现队列的链表结构只能采用头删。我们需要将head所指向的结点进行释放，然后将head向后移动成为新的队头，size减少。但是删除之前我们要对队列内容进行检查，检查队列空间是否为空，只有不为空的情况下才能进行删除。

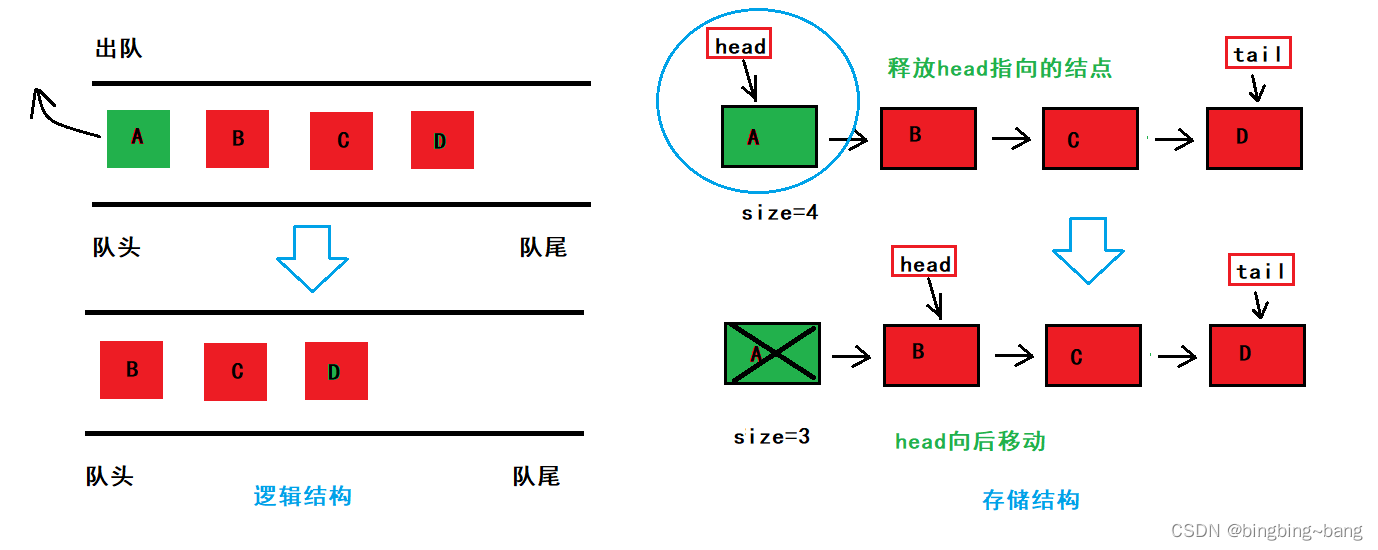
    但是我们要注意只有一个链表结点的情况，此时head和tail均指向该节点，如果直接释放掉head，并将head向后移动，会造成tail指针变为野指针的问题。因此我们需要在释放后，tail指针和head指针一起向后移动。

函数代码：

//队头删除数据
void QueuePop(Queue* pq)
{
    assert(pq);
    assert(!QueueEmpty(pq));
    //只有一个结点
    if ( pq->head == pq->tail )
    {
        free(pq->head);
        pq->head = pq->tail = NULL;
    }
    //其他情况
    else
    {
        QueueNode* next = pq->head->next;
        free(pq->head);
        pq->head = next;
    }
    pq->size--;//元素个数减少
}

2.4获取队头、队尾数据

    队列的数据获取函数是将队头或队尾的数据进行拿出，不改变队列的空间数据结构。获取队头数据直接返回head指针所指向的结点的data，队尾数据则为tail指针指向的结点的data。

** 注意：获取数据函数与删除函数一样，都需要判空，空队列没有数据可以获取，调用函数会获取失败。**

代码函数：

//队头数据拿出
QueueDataType QueueFront(Queue* pq)
{
    assert(pq);
    assert(!QueueEmpty(pq));
    return pq->head->Data;
}

//队尾数据拿出
QueueDataType QueueBack(Queue* pq)
{
    assert(pq);
    assert(!QueueEmpty(pq));
    return pq->tail->Data;
}

2.5队列元素个数计算

    队列元素个数的计算可以采用遍历队列来获取，但是此种方式的时间复杂度为O(N)，当然也可以定义一个全局变量来进行记录，但是此种状况容易代码混乱。本文采用的方式是在创建队列结构时在结构内部定义了一个size来记录数据个数，不会引起代码混乱。size在插入结点或者删除结点的时候随之变化，因此元素个数可直接返回size。

函数代码：

int QueueSize(Queue* pq)
{
    assert(pq);
    return pq->size;
}

2.6队列判空与队列销毁

    判空函数的实现并不复杂，当队列为空时，对应的链表中head指针和tail指针都将指向NULL，我们只需要返回判断即可。

    队列销毁函数就是将队列创建的结点一一释放，其做法与单链表释放一样，采用循环遍历释放即可。

函数代码：

//队列判空
bool QueueEmpty(Queue* pq)
{
    assert(pq);
    return pq->head == NULL;
}
//销毁队列
void QueueDestroy(Queue* pq)
{
    assert(pq);
    QueueNode* cur = pq->head;
    while ( cur)
    {
        QueueNode* next = cur->next;
        free(cur);
        cur = next;
    }
    pq->head = pq->tail = NULL;
}

总结

    只要了解了顺序表和单链表的结构与功能的实现，栈和队列的实现相对简单。本文采用顺序表实现栈，链表实现队列，但是不代表只能这么实现，仁者见仁智者见智，每种实现方式都有存在的意义。C语言标准并没有明确规定，栈与队列必须使用顺序表还是链表实现，两种实现方式均可，但是顺序表具备尾插尾删的优势，因此栈的实现多半采用该结构。链表更适合头删操作，因此队列多采用该种结构进行实现。顺序表与单链表的具体实现方式可以观看本人的系列文章，已放入推荐文章中。本文所讲解的具体代码已放入仓库中，可自行下载参考。

栈实现代码链接：栈的顺序表结构实现 · 67cbfd9 · 冰冰棒/数据结构仓库 - Gitee.com

队列实现代码链接：队列的实现与队列练习题 · 4ff55d4 · 冰冰棒/数据结构仓库 - Gitee.com