AI学习笔记目录:sheng的学习笔记-AI目录-CSDN博客
基础知识
什么是EM算法
EM(Expectation-Maximum)算法也称期望最大化算法,曾入选“数据挖掘十大算法”中,可见EM算法在机器学习、数据挖掘中的影响力。EM算法是最常见的隐变量估计方法,在机器学习中有极为广泛的用途,例如常被用来学习高斯混合模型(Gaussian mixture model,简称GMM)的参数;隐式马尔科夫算法(HMM)、LDA主题模型的变分推断等等。本文就对EM算法的原理做一个详细的总结。
EM算法简介
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation-Maximization Algorithm)。EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其算法基础和收敛有效性等问题在Dempster、Laird和Rubin三人于1977年所做的文章《Maximum likelihood from incomplete data via the EM algorithm》中给出了详细的阐述。其基本思想是:首先根据己经给出的观测数据,估计出模型参数的值;然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计,然后反复迭代,直至最后收敛,迭代结束。
数学知识
极大似然估计
问题描述
假如我们需要调查学校的男生和女生的身高分布 ,我们抽取100个男生和100个女生,将他们按照性别划分为两组。然后,统计抽样得到100个男生的身高数据和100个女生的身高数据。如果我们知道他们的身高服从正态分布,但是这个分布的均值 𝜇 和方差 𝛿2 是不知道,这两个参数就是我们需要估计的。
问题:我们知道样本所服从的概率分布模型和一些样本,我们需要求解该模型的参数。如图1所示。

我们已知的条件有两个:样本服从的分布模型、随机抽取的样本。我们需要求解模型的参数。根据已知条件,通过极大似然估计,求出未知参数。总的来说:极大似然估计就是用来估计模型参数的统计学方法。
用数学知识解决现实问题

最大似然函数估计值的求解步骤

Jensen不等式
定义



EM算法详解
问题描述
我们目前有100个男生和100个女生的身高,但是我们不知道这200个数据中哪个是男生的身高,哪个是女生的身高,即抽取得到的每个样本都不知道是从哪个分布中抽取的。这个时候,对于每个样本,就有两个未知量需要估计:
- 这个身高数据是来自于男生数据集合还是来自于女生?
- 男生、女生身高数据集的正态分布的参数分别是多少?

(1)初始化参数:先初始化男生身高的正态分布的参数:如均值=1.65,方差=0.15
(2)计算每一个人更可能属于男生分布或者女生分布;
(3)通过分为男生的n个人来重新估计男生身高分布的参数(最大似然估计),女生分布也按照相同的方式估计出来,更新分布。
(4)这时候两个分布的概率也变了,然后重复步骤(1)至(3),直到参数不发生变化为止。
EM算法推导流程



EM算法流程

小结
上面介绍的传统EM算法对初始值敏感,聚类结果随不同的初始值而波动较大。总的来说,EM算法收敛的优劣很大程度上取决于其初始参数。
EM算法可以保证收敛到一个稳定点,即EM算法是一定收敛的。
EM算法可以保证收敛到一个稳定点,但是却不能保证收敛到全局的极大值点,因此它是局部最优的算法,当然,如果我们的优化目标 𝑙(𝜃,𝜃𝑙) 是凸的,则EM算法可以保证收敛到全局最大值,这点和梯度下降法这样的迭代算法相同
EM算法是迭代求解最大值的算法,同时算法在每一次迭代时分为两步,E步和M步。一轮轮迭代更新隐含数据和模型分布参数,直到收敛,即得到我们需要的模型参数。
一个最直观了解EM算法思路的是K-Means算法。在K-Means聚类时,每个聚类簇的质心是隐含数据。我们会假设K个初始化质心,即EM算法的E步;然后计算得到每个样本最近的质心,并把样本聚类到最近的这个质心,即EM算法的M步。重复这个E步和M步,直到质心不再变化为止,这样就完成了K-Means聚类。当然,K-Means算法是比较简单的,高斯混合模型(GMM)也是EM算法的一个应用。
EM算法实例



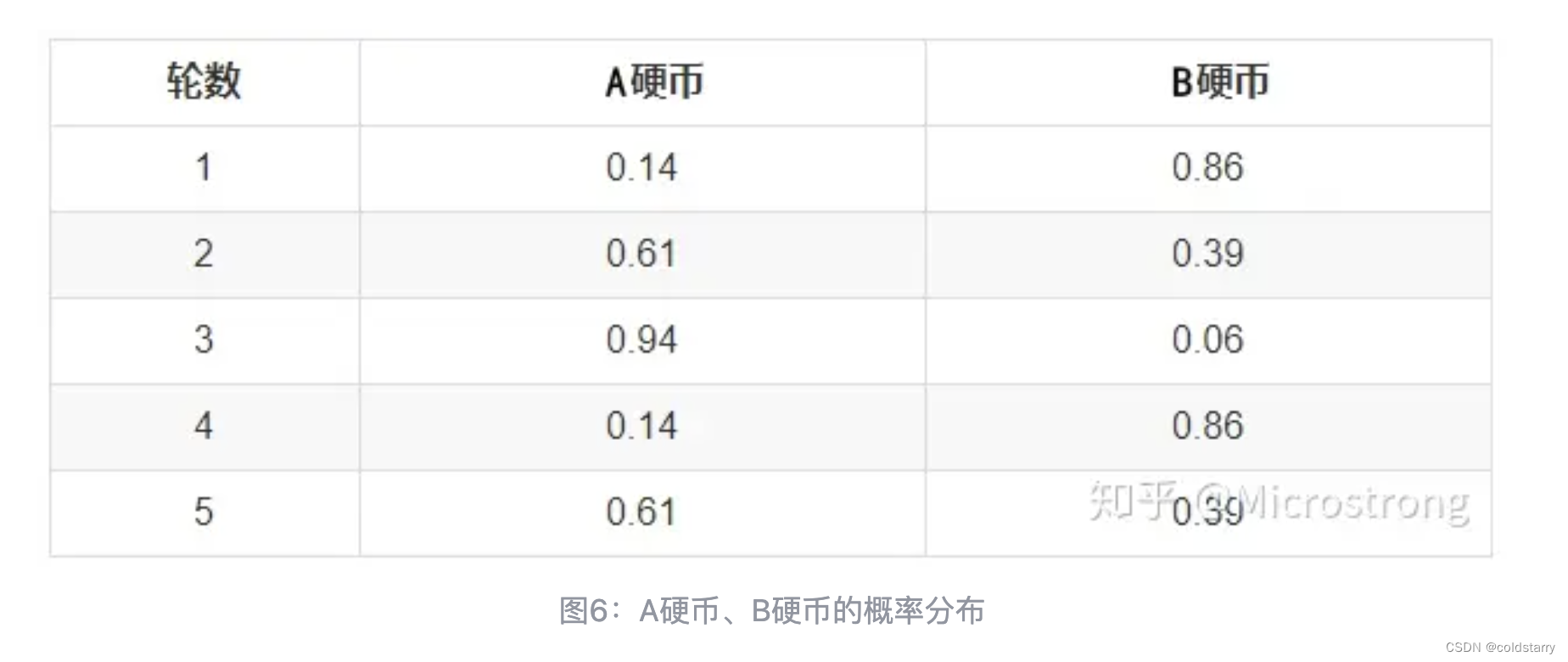
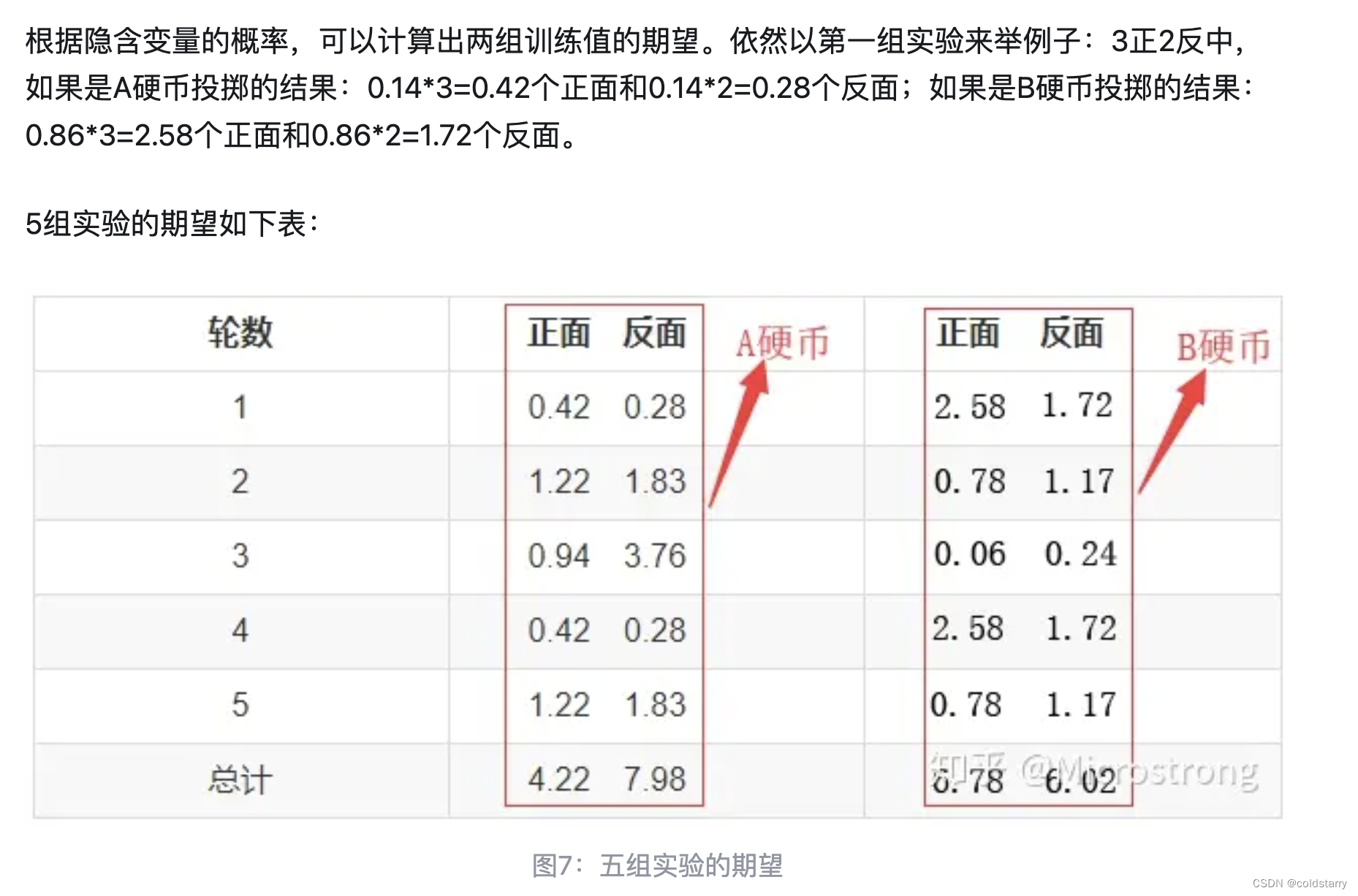

参考文章
EM算法详解 - 知乎
版权归原作者 coldstarry 所有, 如有侵权,请联系我们删除。