1. 认识复杂度和简单排序算法

1. 认识复杂度和简单排序算法

常数时间的操作，一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作。
例子:

int a = arr[i];

时间复杂度为一个算法流程中，常数操作数量的一个指标。常用O(读作big O)来表示。具体来说，先要对一个算法流程非常熟悉，然后去写出这个算法流程中，发生了多少常数操作，进而总结出常数操作数量的表达式。
在表达式中，只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分如果为f(N)，那么时间复杂度为O(f(N))。
评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，也就是“常数项时间”。

1. 选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：

1. 第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置。
2. 然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。
3. 以此类推，直到全部待排序的数据元素的个数为零。

选择排序是不稳定的排序方法。时间复杂度O(n^2)， 空间复杂度O(1)。
例如给定一组数据，[4, 2, 3, 6, 5]其排序过程如以下所示
第一次: [

2

, 4, 3, 6, 5]
第二次: [

2, 3

, 4, 6, 5]
第三次: [

2, 3, 4

, 6, 5]
第四次: [

2, 3, 4, 5

, 6]
第五次: [

2, 3, 4, 5, 6

]

以下是@五分钟学算法大佬的动画，侵删。

java代码实现:

packagepaixu;importjava.util.Arrays;publicclassCode01_SelectionSort{publicstaticvoidmain(String[] args){int[] arr ={4,2,3,6,5};selectionSort(arr);System.out.println(Arrays.toString(arr));}publicstaticvoidselectionSort(int[] arr){if(arr ==null|| arr.length <2){return;}for(int i =0; i < arr.length -1; i++){int minIndex = i;for(int j = i +1; j < arr.length; j++){
                minIndex = arr[j]< arr[minIndex]? j : minIndex;}swap(arr, i, minIndex);}}publicstaticvoidswap(int[] arr,int i,int j){int tmp = arr[i];
        arr[i]= arr[j];
        arr[j]= tmp;}}

2. 冒泡排序

冒泡排序的英文Bubble Sort，是一种最基础的交换排序。之所以叫做冒泡排序，因为每一个元素都可以像小气泡一样，根据自身大小一点一点向数组的一侧移动。冒泡排序算法的原理如下：

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

冒泡排序是稳定的排序方法。时间复杂度O(n^2)， 空间复杂度O(1)。

java代码:

packagepaixu;importjava.util.Arrays;publicclassCode02_BubbleSort{publicstaticvoidmain(String[] args){int[] arr ={6,4,1,2,9,3,7,8,10,5};bubbleSort(arr);System.out.println(Arrays.toString(arr));}publicstaticvoidbubbleSort(int[] arr){if(arr ==null|| arr.length <2){return;}for(int e = arr.length -1; e >0; e--){boolean flag =true;for(int i =0; i < e; i++){if(arr[i]> arr[i +1]){swap(arr, i, i +1);
                    flag =false;}}if(flag){break;}}}publicstaticvoidswap(int[] arr,int i,int j){
        arr[i]= arr[i]^ arr[j];
        arr[j]= arr[i]^ arr[j];
        arr[i]= arr[i]^ arr[j];//        int tmp = arr[i];//        arr[i] = arr[j];//        arr[j] = tmp;}}

3. 异或运算

异或运算资源来自 https://blog.csdn.net/weixin_43614026/article/details/104341932

如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。异或也叫半加运算，其运算法则相当于不带进位的二进制加法：二进制下用1表示真，0表示假，则异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1），这些法则与加法是相同的，只是不带进位，所以 异或常被认作不进位加法。（来源于搜狗百科）

例如，计算 1011101^1000011: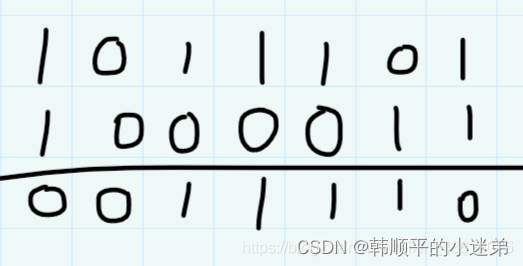

异或性质与扩展
（用不进位相加较好理解）

• 0 ^ N = N
• N ^ N = 0

异或运算满足交换律和结合律

• c =a ^ b =b ^ a
• c =（ a ^ b ）^ c = a ^ ( b ^ c )

不用额外变量交换两个数：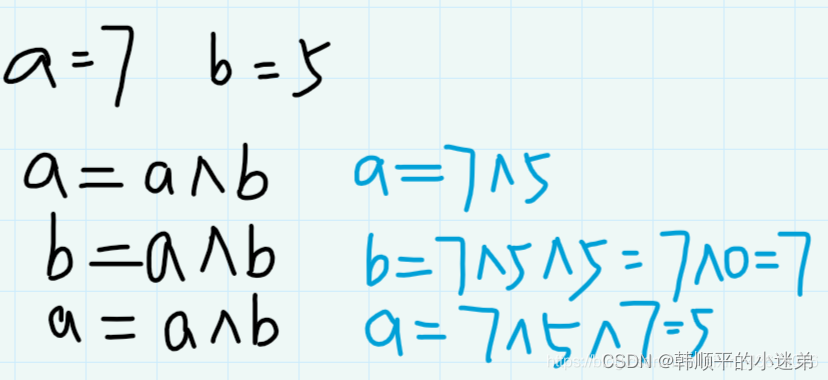

• 一个数组中有一种数出现了奇数次，其他数都出现了偶数次，怎么找到这个数？ 例如，该数组为 a[]={1, 2, 2, 3, 3} 将所有的数全部异或运算，运算结果就是出现了奇数次的数。
• 一个数组中有两种出现了奇数次，其他数都出现了偶数次，怎么找到这两个数？ 例如，该数组为a[]={1,2,4,4,5,5}，分析步骤如下:

1. 让该数组中所有的数字做异或运算，那么设结果 eor == a ^ b != 0 ;
2. 因为eor 不为 0 ，则可以假设 a 与 b在某位上，比如在第三位上，a第三位是1，则b的第三位为0；
3. 在其余的出现偶数次的数字中，找出所有在第三位为1的数；
4. 用变量 eor’ 与这个数组中所有第三位为1的数做异或运算 ，则 eor’ 最终的答案为a，因为所有第三位为1的数字，除了a，其余为偶数 个，异或运算后为0。(因为除了a 与 b ，其余数字的个数都为偶数个，那么可以确定第三位为1的和第三位为0的个数都为偶数个。因为 eor = a ^ b,且其余偶数运算之后结果为0，如果第三位为1的数字个数为奇数，那么第三位为0的数字个数也为奇数，那么将他们全部进行异或运算后，第三位数字为1，不为0，与实际不符。)
5. 再用eor与eor’做异或运算，即a ^ b ^ a = b;

以下给出该题解的代码：首先了解如何取到该数最右端的1，就是该数取反+1再&该数 （核心：int rightOne = eor & ( ~ eor + 1 ); ）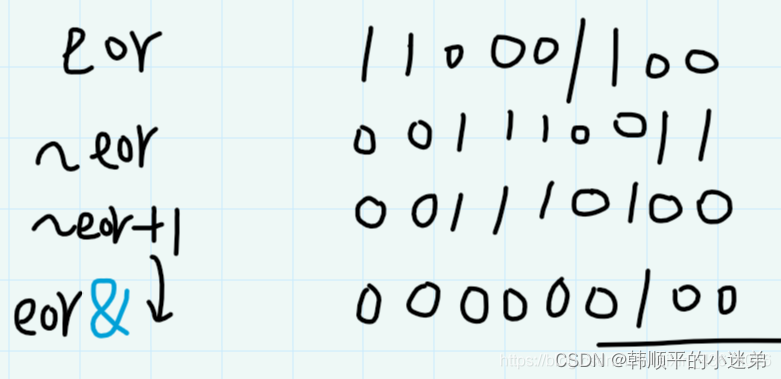

java代码:

packagepaixu.class01;publicclassCode07_EvenTimesOddTimes{publicstaticvoidmain(String[] args){int[] arr ={1,2,4,4,5,5};printOddTimesNum2(arr);}publicstaticvoidprintOddTimesNum2(int[] arr){int eor =0, onlyOne =0;for(int curNum : arr){
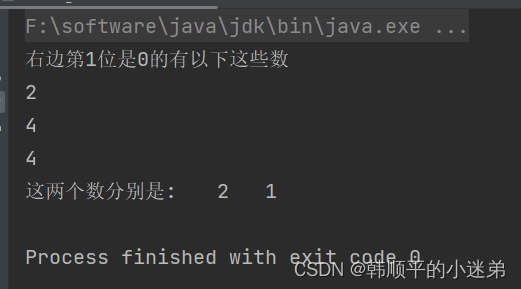
            eor ^= curNum;}//eor = a ^ b//eor != 0//eor 必然有一个位置上是 1int rightOne = eor &(~eor +1);//提取出最右的1System.out.println("右边第"+ rightOne +"位是0的有以下这些数");for(int cur : arr){if((cur & rightOne)==0){System.out.println(cur);
                onlyOne ^= cur;}}System.out.println("这两个数分别是:\t"+ onlyOne +"\t"+(onlyOne ^ eor));}}

4. 插入排序

插入排序的原理：
一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数增 1的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动 。
选择排序的基本思想是：

将未排序的元素一个一个地插入到有序的集合中，插入时把所有有序集合从后向前扫一遍，找到合适的位置插入。

插入排序是稳定的排序方法。时间复杂度O(n^2)， 空间复杂度O(1)。
下图来源 https://blog.csdn.net/hcz666/article/details/126488359。插入排序的过程如下：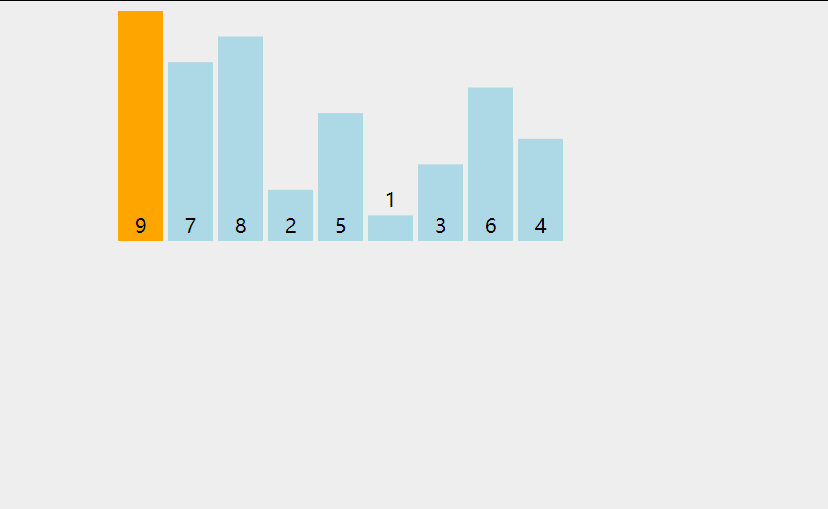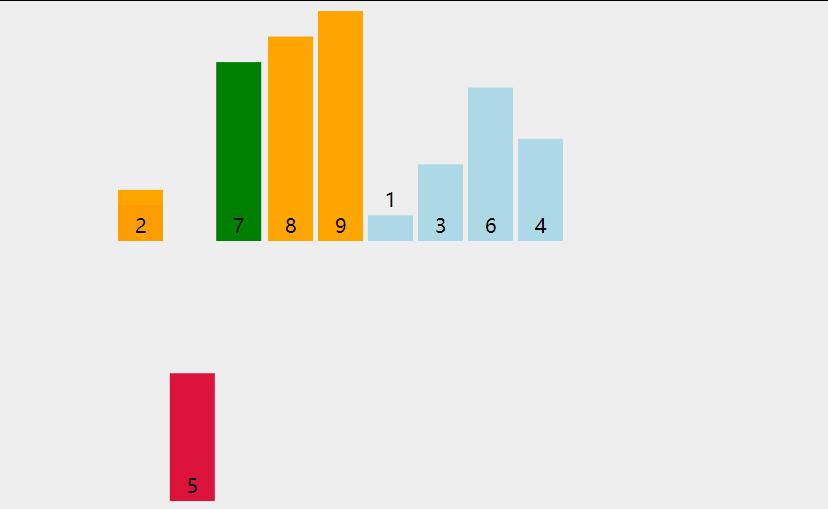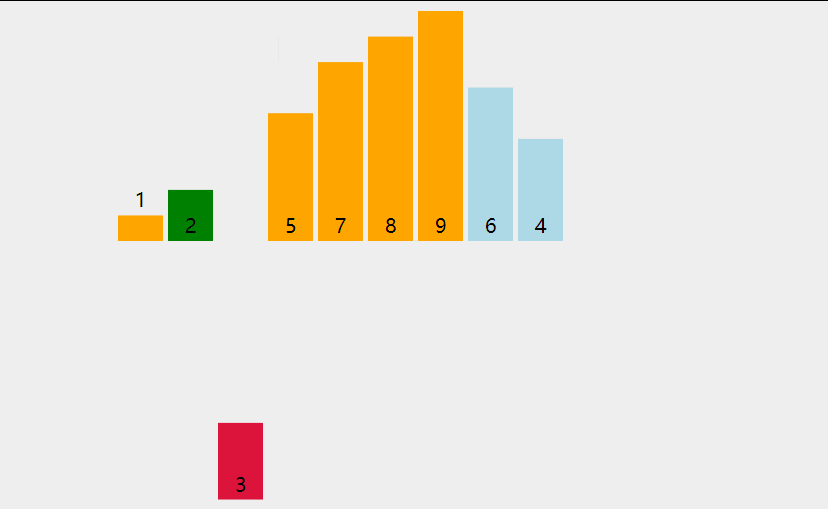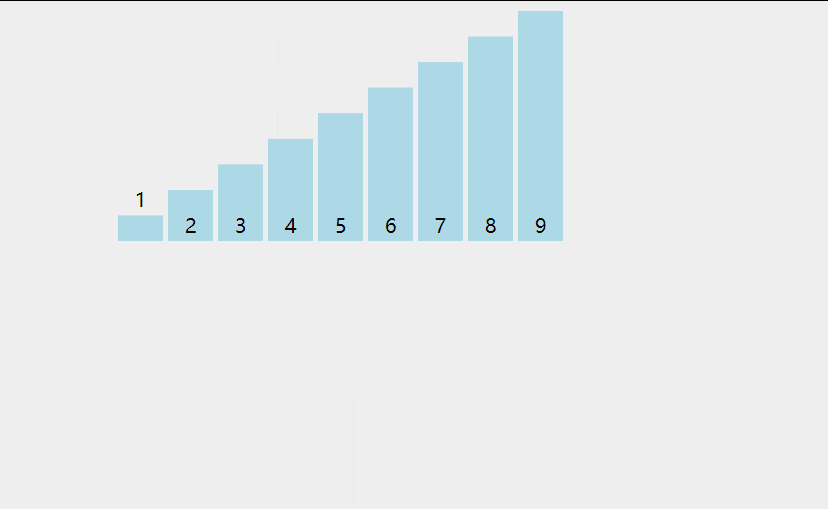

java代码:

packagepaixu.class01;importjava.util.Arrays;publicclassCode03_InsertSort{publicstaticvoidmain(String[] args){int[] arr ={9,7,8,2,5,1,3,6,4};insertionSort(arr);System.out.println(Arrays.toString(arr));}publicstaticvoidinsertionSort(int[] arr){if(arr ==null|| arr.length <2){return;}//0~0 有序//0~i 想有序for(int i =1; i < arr.length; i++){// 0~i 做到有序for(int j = i -1; j >=0&& arr[j]> arr[j +1]; j--){swap(arr, j, j +1);}}}publicstaticvoidswap(int[] arr,int i,int j){
        arr[i]= arr[i]^ arr[j];
        arr[j]= arr[i]^ arr[j];
        arr[i]= arr[i]^ arr[j];}}

5. 二分法的详解与扩展

• 在一个有序数组中，找某个数是否存在。时间复杂度O(logN) java代码:

packagepaixu.class01;publicclassCode04_BSExist{publicstaticvoidmain(String[] args){int[] sortedArr ={1,2,3,4,5,6,7,8,9};System.out.println(exist(sortedArr,5));}publicstaticbooleanexist(int[] sortedArr,int num){intL=0;intR= sortedArr.length -1;while(L<=R){int mid =L+((R-L)>>1);if(sortedArr[mid]== num){System.out.println("目标数下标:"+ mid);returntrue;}if(sortedArr[mid]> num){R= mid -1;}else{L= mid +1;}}returnfalse;}}

• 在一个有序数组中， 找>=某个数最左侧的位置

java代码

packagepaixu.class01;publicclassCode05_BSNearLeft{publicstaticvoidmain(String[] args){int[] arr ={1,2,3,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5,6,6,6,6};System.out.println("最左边的值为:"+nearestIndex(arr,6));}// 在arr上，找满足>=value的最左位置publicstaticintnearestIndex(int[] arr,int value){intL=0;intR= arr.length -1;int index =-1;while(L<=R){int mid =L+((R-L)>>1);if(arr[mid]>= value){R= mid -1;
                index = mid;}else{L= mid +1;}}return index;}}

• 局部最小值问题题目描述 局部最小值定义：

1. 最左边边界处，如果最左边的数小于左边第二个数，则最左边为局部最小值。
2. 最右边边界处，如果最右边的数小于右边第二个数，则最右边为局部最小值。
3. 中间处，如果一个数小于它两边的数，则这个数就是局部最小值。

说白了，就是二维坐标系中的任意一个最低点，都是局部最小值。现在，有一个数组，相邻的两个数不相等，请求出一个数组中的一个局部最小值。
算法思路

1. 首先，先观察最左边的第一个和第二个数，判断是否是局部最小值。
2. 然后，再观察最右边第一个和第二个数，判断是否是局部最小值。
3. 如果最左边和最右边有一个是局部最小值，则此题结束。
4. 否则，说明一个什么问题？说明左边的曲线是向下递减的，右边的曲线也是向上递增的，对吧？那么，中间是必定有局部最小值的，这是在高数最大值最小值中有类似的定义，对吧？
5. 然后，直接用二分法，选取中间的数，判断其是不是局部最小值？如果不是的话，观察他左右趋势，假如，它左边一个数比他小，说明什么？说明它左边是递增的，而此时最左边的递减的，通过上面分析4的判断，说明它左边存在局部最小值，然后，再其左边区间，再次二分法，直到找到局部最小值。

总结:
这题代码其实就是二分查找。关键是此题的思路，这是重点，此题说明了，二分查找并不一定只能求解有序数组中的某个数。在一些能够直接排除掉一半区间的例子中，也同样可以使用二分法来解决，将时间复杂度直接降低到O(logn)。
就比如此题，可以根据一个区间两边的递增递减性，来判断区间内是否有局部最小值，那么，就可以直接用二分法从中间划分，然后根据判断条件，可以直接排除掉一半区间。

java代码:

packagepaixu.class01;publicclassCode09_FindOneLessValueIndex{publicstaticvoidmain(String[] args){int[] arr ={6,5,3,4,6,7,8};int[] arr1 ={1,2,3,4,5,6,7,8};int[] arr2 ={2,1,3,4,5,6,8,7};System.out.println("(中间情况)arr局部最小索引为:"+getLessIndex(arr)+"\t值为"+ arr[getLessIndex(arr)]);System.out.println("(左边情况)arr1局部最小索引为:"+getLessIndex(arr1)+"\t值为"+ arr1[getLessIndex(arr1)]);System.out.println("(右边情况)arr2局部最小索引为:"+getLessIndex(arr2)+"\t值为"+ arr2[getLessIndex(arr2)]);}publicstaticintgetLessIndex(int[] arr){if(arr ==null|| arr.length ==0){return-1;// no exist}//1.先观察最左边的第一个和第二个数，判断是否是局部最小值if(arr.length ==1|| arr[0]< arr[1]){return0;}//2.再观察最右边第一个和第二个数，判断是否是局部最小值if(arr[arr.length -1]< arr[arr.length -2]){return arr.length -1;}//3.局部最小值在中间intL=1;intR= arr.length -2;while(L<=R){int mid =L+((R-L)>>1);if(arr[mid]< arr[mid -1]&& arr[mid]< arr[mid+1]){return mid;}if(arr[mid]< arr[mid+1]){R= mid -1;}else{L= mid +1;}}return-1;}}

6. 对数器的概率和使用

1. 有一个你想要测的方法a
2. 实现复杂度不好但是容易实现的方法b
3. 实现一个随机样本产生器
4. 把方法a和方法b跑相同的随机样本，看看得到的结果是否一样。
5. 如果有一个随机样本使得比对结果不一致，打印样本进行人工干预，改对方法a或者方法b
6. 当样本数量很多时比对测试依然正确，可以确定方法a已经正确。