笛卡尔树的构建过程与性能优化策略

本文收录于专栏：算法之翼

笛卡尔树的构建过程与性能优化策略

笛卡尔树（Cartesian Tree）是一种结合了堆和二叉搜索树性质的数据结构，具有重要的应用场景，如区间查询和动态数组处理。本文将介绍笛卡尔树的构建过程，并对其平衡性进行深入分析，同时提供相应的代码实例。

什么是笛卡尔树？

笛卡尔树是一种特殊的二叉树，满足以下两个性质：

1. 堆性质：每个节点的键值（key）满足父节点的键值大于或等于其子节点的键值。
2. 二叉搜索树性质：节点的序号（index）满足二叉搜索树的特性，即左子树节点的序号小于根节点，右子树节点的序号大于根节点。

可以将笛卡尔树看作是一种融合了堆和二叉搜索树特性的结构，用来处理需要同时维护优先级和序列关系的问题。

笛卡尔树的应用

笛卡尔树通常用于解决以下问题：

1. 动态序列数据的区间最小值/最大值查询。
2. 区间划分与归并问题。
3. 文本编辑器的自动格式调整。

笛卡尔树的构建过程

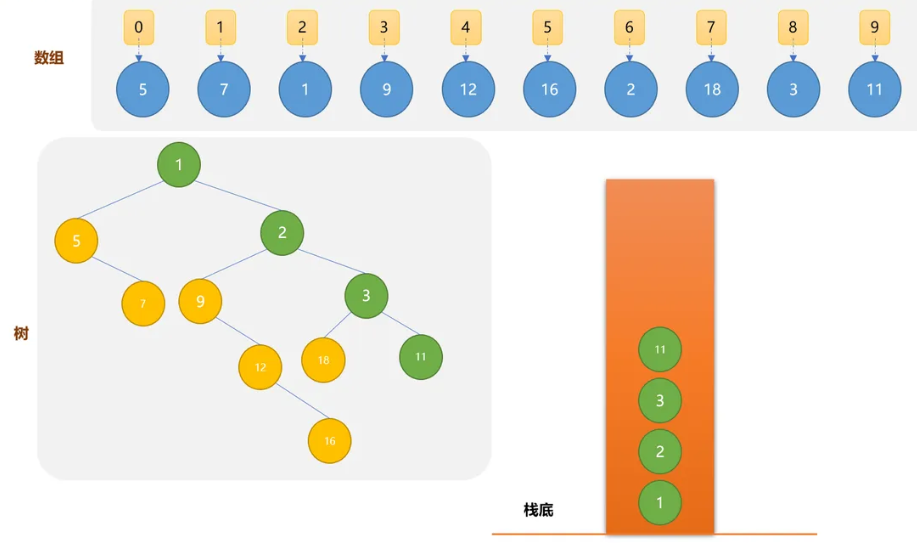
构建笛卡尔树有多种方法，本文介绍的构建方式基于中序遍历顺序。假设我们有一组数据对

(index, key)

，其中

index

是数据在序列中的位置，

key

是优先级，我们将通过这些对来构造笛卡尔树。

算法步骤

1. 按照 index 顺序依次处理数据对 (index, key)。
2. 对于每个新的节点，找到其适当的父节点。如果当前节点的 key 小于父节点的 key，则将其作为父节点的子树根。
3. 使用栈来维护当前的节点序列，以便快速找到父节点并更新子树结构。

代码实例

下面是一个用 Python 实现的笛卡尔树构建过程：

classTreeNode:def__init__(self, index, key):
        self.index = index  # 序号
        self.key = key      # 键值
        self.left =None# 左子树
        self.right =None# 右子树defbuild_cartesian_tree(data):
    stack =[]
    root =Nonefor index, key inenumerate(data):
        current = TreeNode(index, key)# 维护栈，确保栈顶节点的key小于当前节点while stack and stack[-1].key > key:
            current.left = stack.pop()if stack:
            stack[-1].right = current
        else:
            root = current

        stack.append(current)return root

# 数据集，index为数组下标，key为对应的值
data =[3,2,6,1,9,5]
root = build_cartesian_tree(data)# 笛卡尔树的中序遍历definorder_traversal(node):if node:
        inorder_traversal(node.left)print(f'Index: {node.index}, Key: {node.key}')
        inorder_traversal(node.right)# 打印树的中序遍历结果
inorder_traversal(root)

代码说明

• TreeNode 类定义了笛卡尔树的节点结构，包括 index、key 以及 left 和 right 子树。
• build_cartesian_tree 函数通过遍历 data 构建笛卡尔树，维护了一个栈来确保堆的性质，同时根据二叉搜索树的性质调整左右子树。
• inorder_traversal 函数用于验证生成的树是否符合二叉搜索树的特性，按序打印节点信息。

笛卡尔树的平衡性分析

笛卡尔树的平衡性取决于数据中

key

的分布情况。以下是几种特殊情况下的平衡性分析：

最优情况

如果

key

的分布是“理想的”，例如数据基本有序（升序或降序），笛卡尔树将趋近于一棵平衡树。此时树的高度为

O(log n)

，可以达到最优的查询和插入性能。

最差情况

如果

key

的分布是极端的，例如所有

key

都是严格递增或递减，笛卡尔树将退化为一棵链式结构，类似于一个线性链表。此时树的高度为

O(n)

，查询和插入的复杂度也相应地增加到线性时间。

一般情况

在实际应用中，

key

的分布往往是随机的，因此笛卡尔树的平均高度约为

O(log n)

，其性能接近于平衡二叉树，能够在大多数情况下提供高效的查询和插入操作。

平衡性优化

为了提高笛卡尔树的平衡性，可以在插入新节点时随机选择

key

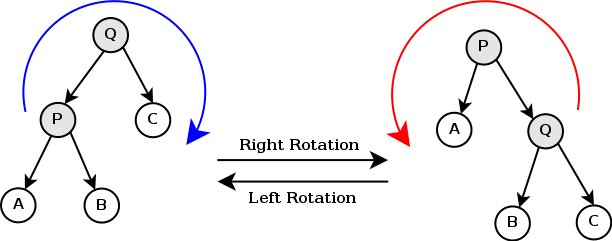
，或者采用类似于 AVL 树或红黑树的旋转操作，以维持树的高度接近于对数级别。

笛卡尔树的插入操作

在笛卡尔树中，插入操作需要保持树的两个性质：堆性质和二叉搜索树性质。插入一个新的节点时，我们可以采用类似于构建时的方式，保证堆性质的同时更新树的左右子树。

插入算法步骤

1. 从根节点开始，找到插入位置，保证新的节点遵循二叉搜索树的性质。
2. 如果新节点的 key 小于当前节点的 key，则需要调整树结构，保证堆性质，可能需要将新节点插入到树的某个子树中，或者进行节点的旋转操作。
3. 在插入过程中，继续维护笛卡尔树的平衡性。

插入操作的代码实现

我们可以在之前的笛卡尔树代码基础上扩展插入操作：

definsert(root, index, key):
    new_node = TreeNode(index, key)# 如果树为空，直接返回新节点ifnot root:return new_node
    
    # 寻找插入位置if index < root.index:
        root.left = insert(root.left, index, key)# 插入后需要检查堆性质if root.left and root.left.key < root.key:
            root = rotate_right(root)else:
        root.right = insert(root.right, index, key)# 插入后检查堆性质if root.right and root.right.key < root.key:
            root = rotate_left(root)return root

# 右旋操作，用于保持堆性质defrotate_right(node):
    new_root = node.left
    node.left = new_root.right
    new_root.right = node
    return new_root

# 左旋操作，用于保持堆性质defrotate_left(node):
    new_root = node.right
    node.right = new_root.left
    new_root.left = node
    return new_root

# 插入操作示例
root =None
data =[(0,3),(1,2),(2,6),(3,1),(4,9),(5,5)]for index, key in data:
    root = insert(root, index, key)

inorder_traversal(root)

代码说明

• insert 函数实现了笛卡尔树的插入逻辑。我们首先根据 index 寻找插入位置，同时保证二叉搜索树的性质。插入新节点后，检查是否需要旋转来维持堆性质。
• rotate_right 和 rotate_left 函数分别实现了右旋和左旋，用来调整树结构，保证堆的性质。

插入的时间复杂度

在最优情况下（树为平衡二叉树），插入操作的时间复杂度为

O(log n)

。在最坏情况下（树退化为链表），插入操作的时间复杂度为

O(n)

。为了保证插入操作的效率，我们可以在插入时通过旋转操作保持树的平衡性。

笛卡尔树的删除操作

删除操作与插入类似，也需要保持笛卡尔树的两个性质。删除一个节点时，我们首先需要找到该节点，然后删除它，并通过旋转操作调整子树结构，保证堆和二叉搜索树的性质。

删除算法步骤

1. 找到要删除的节点，确保二叉搜索树的性质不被破坏。
2. 将该节点从树中删除，如果它有子节点，则需要通过旋转操作将子节点接到正确的位置。
3. 维护树的堆性质，确保子树的根节点 key 大于等于其子节点的 key。

删除操作的代码实现

下面是删除操作的实现：

defdelete(root, index):ifnot root:returnNone# 寻找要删除的节点if index < root.index:
        root.left = delete(root.left, index)elif index > root.index:
        root.right = delete(root.right, index)else:# 找到要删除的节点ifnot root.left andnot root.right:returnNoneelifnot root.left:
            root = rotate_left(root)elifnot root.right:
            root = rotate_right(root)else:# 比较左右子树的key值，选择合适的旋转方向if root.left.key < root.right.key:
                root = rotate_right(root)else:
                root = rotate_left(root)# 继续递归删除当前节点
        root = delete(root, index)return root

# 删除操作示例
root = delete(root,3)# 删除index为3的节点
inorder_traversal(root)

代码说明

• delete 函数用于删除笛卡尔树中的节点。在删除节点后，我们通过旋转操作调整子树结构，保持堆和二叉搜索树的性质。
• 该实现递归地查找并删除节点，保证删除后的树仍然满足笛卡尔树的性质。

删除的时间复杂度

和插入操作一样，删除操作的时间复杂度取决于树的高度。在最优情况下，删除操作的时间复杂度为

O(log n)

，而在最坏情况下（树退化为链表），时间复杂度为

O(n)

。

笛卡尔树的平衡性维护

为了在笛卡尔树中高效地进行插入和删除操作，我们需要保持树的平衡性。前面提到，通过旋转操作可以保持堆性质，但这些旋转操作在维护堆性质的同时，也会破坏树的平衡性。因此，在实际应用中，我们可以引入类似 AVL 树或红黑树的平衡机制，使得笛卡尔树在操作后能够快速恢复平衡。

一种常见的方法是：

• 随机化插入：在插入时，随机生成 key 值，使得树的形状更趋向于平衡。
• 平衡旋转：通过适当的旋转操作在插入和删除后保持树的平衡性。

这些方法能够有效减少最坏情况下树退化为链表的风险，从而提高操作的平均时间复杂度。

笛卡尔树的应用场景

笛卡尔树的构建与平衡性分析不仅仅是一个理论问题，它在实际应用中具有多种用途，特别是在处理复杂的查询与动态数据集时，笛卡尔树可以高效地解决某些问题。下面将介绍几个笛卡尔树的典型应用场景。

1. 区间查询问题

笛卡尔树可以用于高效解决区间查询问题，尤其是当我们需要对区间进行动态调整时。因为笛卡尔树同时具备二叉搜索树的性质和堆的性质，它可以支持快速的区间最小值或最大值查询。

示例：区间最小值查询

考虑一个数组，我们需要频繁地查询某个区间的最小值。使用笛卡尔树构建这个数组后，基于二叉搜索树的性质可以快速定位到所需的区间，而堆性质确保了我们可以快速获得该区间的最小值。

defrange_min_query(root, left, right):ifnot root:returnfloat('inf')# 当前节点的索引在区间范围外if root.index < left:return range_min_query(root.right, left, right)elif root.index > right:return range_min_query(root.left, left, right)# 当前节点的索引在区间范围内，返回最小值returnmin(root.key, 
               range_min_query(root.left, left, right), 
               range_min_query(root.right, left, right))# 查询区间[1, 4]的最小值
min_value = range_min_query(root,1,4)print(f"The minimum value in range [1, 4] is: {min_value}")

2. 动态顺序统计

在笛卡尔树中，每个节点都可以维护子树的大小，这使得我们能够快速计算节点在有序集合中的排名。结合笛卡尔树的二叉搜索树性质，我们可以实现动态的顺序统计操作，如查找某个节点在当前集合中的排名，或者根据排名查找节点。

**示例：查找第

k

小的元素**

defkth_smallest(root, k):ifnot root:returnNone
    
    left_size = root.left.size if root.left else0# 当前节点就是第k小的元素if left_size +1== k:return root.index
    
    # 第k小的元素在左子树中if k <= left_size:return kth_smallest(root.left, k)# 第k小的元素在右子树中return kth_smallest(root.right, k - left_size -1)# 查找第3小的元素
kth = kth_smallest(root,3)print(f"The 3rd smallest element is: {kth}")

3. 笛卡尔树与其他数据结构的结合

笛卡尔树能够与其他数据结构（如平衡树或堆）结合使用，以解决某些复杂的动态查询问题。例如，可以在平衡树上维护多个笛卡尔树，以实现复杂的区间合并和查询操作。这种组合数据结构在某些领域（如计算几何）中非常有用。

笛卡尔树的平衡性优化

在实际应用中，构建一棵理想的笛卡尔树需要考虑树的平衡性，避免树结构退化为线性链表。为了保证树的平衡性，我们可以借鉴一些来自其他平衡树（如 AVL 树、红黑树）的技术。

1. 随机化构建

一种常见的平衡性优化方法是采用随机化构建策略，即在构建笛卡尔树时，随机生成节点的

key

值，使得生成的树更趋于平衡。随机化构建的好处在于它能够在大多数情况下避免树的退化，提高操作的平均时间复杂度。

import random

defrandom_cartesian_tree(data):
    random.shuffle(data)
    root =Nonefor index, key in data:
        root = insert(root, index, key)return root

# 随机化构建笛卡尔树
data =[(0,3),(1,2),(2,6),(3,1),(4,9),(5,5)]
root = random_cartesian_tree(data)
inorder_traversal(root)

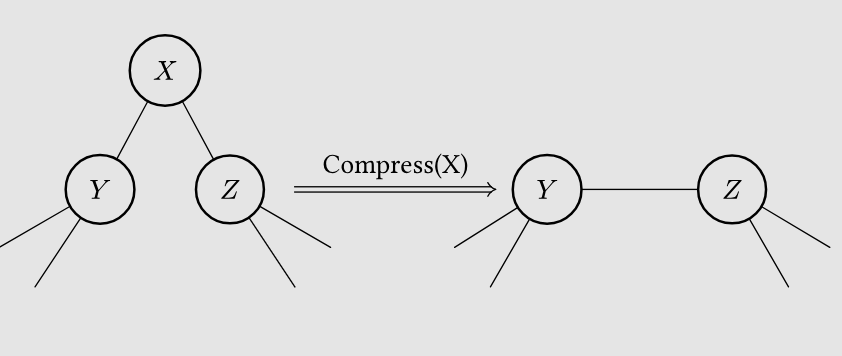
2. 旋转操作优化

另一种方法是通过增加旋转操作来主动平衡树。在插入和删除操作时，我们可以通过左旋或右旋来确保树的平衡性。与 AVL 树或红黑树的旋转操作类似，这种方法能够确保树的高度始终保持在

O(log n)

以内。

结语

笛卡尔树是一种强大的数据结构，通过结合堆和二叉搜索树的性质，它能够高效解决多个复杂问题，如区间查询、顺序统计等。通过引入平衡性维护机制，笛卡尔树能够在动态数据集上提供稳定的性能表现。

在实际应用中，笛卡尔树不仅能够单独使用，还可以与其他数据结构结合，解决特定领域中的复杂问题。无论是在理论分析还是在实际场景中，笛卡尔树的构建与优化都是非常值得研究和应用的方向。