非参数检验之符号检验、Wilcoxon符号秩检验、游程检验

一、符号检验

广义符号检验是对连续变量π分位点 xn 进行的检验，而狭义的符号检验则是针对中位数M= Q0.5

进行的检验。

例2.1下面是世界上71个大城市的花费指数(包括租金)按递增次序排列如下(这里上海是44位，其指数为63.5）：

27.8 27.8 29.1 32.2 32.7 32.7 36.4 36.5 37.5 37.7 38.8 41.9 45.2 45.8 46 47.6 48.2 49.9 51.8 52.7 54.9 55 55.3 55.5 58.2 60.8 62.7 63.5 64.6 65.3 65.3 65.3 65.4 66.2 66.7 67.7 71.2 71.7 73.9 74.3 74.5 76.2 76.6 76.8 77.7 77.9 79.1 80.9 81 82.6 85.7 86.2 86.4 89.4 89.5 90.3 90.8 91.8 92.8 95.2 97.5 98.2 99.1 99.3 100 100.6 104.1 104.6 105 109.4 122.4

请检验以下问题：

（1）有人说64是中位数（样本中位数为67.7，大于64）

（2）有人说64是下四分位数（样本下四分位数为50.85，小于64）

回答如下：

若想知道样本下四分位点 $Q_{0.25}$ 是否小于64的检验.形式上，我们的检验是:

$H0:Q_{0.25}=64\Leftrightarrow H1:Q_{0.25}<64$

（1）这里的64就是 $q_{0}$ .按照零假设，小于64的样本点个数 $Q_{0.25}S^-$ 的实现值 $s^-$ 应该大约占样本的1/4，或者 $S^-$ 服从Bin(n,0.25)分布.如果偏离得太远，就有问题了.容易算出 $S^-$ =28， $s^+$ =43和n= $s^-+s^+$ =71.根据上面的说明，对于这个例子，p值=1- $P_{H0}$ (K≤ $s^-$ -1)=1- $P_{H0}$ (K≤28-1)=1- $P_{H0}$ (K≤27)≈0.00515.因此，可以对于显著性水平α=0.01，拒绝零假设，即下四分位点 $Q_{0.25}$ 应该小于64.再看关于64是否为中位数的检验，

$H_0:M(=Q__{0.5})=M_0\Leftrightarrow H_1:M>64$

（2）同样， $s^-=28, s^+=43$ 和 $n=s^-+s^+=71$ *.*但是这里涉及的零假设下的分布为Bin(71,0.5),而不是刚才的Bin(71,0.25).取k=min( $s^-,s^+$ )=28,p值=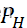。(K≤k)=(K≤28) ≈0.04796.

R代码：

sign.test=function(x,p,M0)   #x为数据，p为分位数，M0为待检验的的数
{s1=sum(x<M0);s2=sum(x>M0);n=s1+s2
p1=pbinom(s1,n,p);p2=1-pbinom(s1-1,n,p)
if (p1>p2) m1="H0: M>=M0"
else m1="H0: M<=M0"
p.value=min(p1,p2);p.value2=2*p.value
list(c("s+"=s2,"s-"=s1,"n'"=n),c("原假设"=m1,"单边p值"=p.value,"双边p值"=p.value2))
}
setwd("C:/Users/Lenovo/Desktop/data")
x1<-read.table("ExpensiveCities.TXT",sep=" ")
sign.test(x1,0.5,64)
sign.test(x1,0.25,64)

代码运行结果：

二、Wilcoxon符号秩检验

在Wilcoxon符号秩检验中，它把观测值和零假设的中心位置之差的绝对值的秩分别按照不同的符号相加作为其检验统计量。它适用于T检验中的成对比较，但并不要求成对数据之差di服从正态分布，只要求对称分布即可。检验成对观测数据之差是否来自均值为0的总体（产生数据的总体是否具有相同的均值）。

例2.3下面是10个欧洲城镇每人每年平均消费的酒类相当于纯酒精数（单位：升）.数据已经按照升幂排列.

4.12 5.81 7.63 9.74 10.39 11.92 12.32 12:89 13.54 14.45

人们普遍认为欧洲各国人均年消费酒量的中位数相当于纯酒精8升，我们希望用上述数据来检验这种看法.

解题过程：

设即零假设为：对上述数据的计算得到中位数为因此，我们的备选假设为：符号秩检验步骤如下：设 $M_{0}$ =8,即零假设为H0：M=8.对上述数据的计算得到中位数为11.160.因此，我们的备选假设为H1：M>8.Wilcoxon符号秩检验步骤如下：

（1）对计算，它们代表这些样本点到的距离，对于例数据，则计算，得到、、、、、、、、、(1)对i=1,…,n,计算| $X_i$ − $M_{0}$ l，它们代表这些样本点到M0的距离，对于例2.3数据，则计算| $X_i$ −8|,i=1,…，10,得到：

3.88、2.19、0.37、1.74、2.39、3.92、4.32、4.89、5.54、6.45.

(3)把上面的n个绝对值排序，并找出它们的n个秩.如果有相同的样本点，每个点取平均秩.对于例2.3数据，这些秩为5、3、1、2、4、6、7、8、9、10

（3）令 $W^+$ 等于 $X_i-M_0>0$ 的 $|X_i-M_0|$ 的秩的和.而W−等于 $X_i-M_0<0$ 的 $|X_i-M_0|$ 的秩的和.注意： $W^++W^-=n(n+1)/2$ .对于例2.3数据，加上符号的秩为−5、−3、−1、2、4、6、7、8、9、10

因此， $W^+=2+4+6+7+8+9+10=46$ 和 $W^-=5+3+1=9.$

(4）对双边检验 $H_0...M=M_0\Leftrightarrow H_1...M\neq M_0$ ，在零假设下，W+和W−应差不多，因而，当其中之一很小时，应怀疑零假设，在此，取检验统计量 $W=min(W^+,W^-)$ .类似地，对于单边检验 $H_0...M\leqslant M_0\Leftrightarrow H1...M>M_0$ ,取 $W=W^-$ ，对单边检验: $H_0...M\geqslant M_0\Leftrightarrow H1...M<M_0$ ,取 $W=W^+$ .对于例2.3的问题，取 $W=W^-=9$ .

(5)根据得到的W值，利用统计软件或查Wilcoxon符号秩检验的分布表以得到在零假设下的p值.得到p值为0.032.

(6）如果p值较小（比如小于或等于给定的显著性水平，譬如0.05）则可以拒绝零假设.如果p值较大则没有充分证据来拒绝零假设，但不意味着接受零假设.对于例2.3的问题，如果给定α=0.05,由于p值（=0.032）小于α,我们可以拒绝零假设，认为欧洲人均酒精年消费多于8升.

R代码：

y<-c(4.12,5.81,7.63,9.74,10.39,11.92,12.32,12.89,13.54,14.45)
wilcox.test(y-8,alt="greater")
wilcox.test(y-12.5,alt="less")
walsh=NULL;for(i in 1:10)for(j in i:10)
walsh=c(walsh,(y[i]+y[j])/2);walsh=sort(walsh)
qsignrank(0.025,10)

代码运行结果如下：

三、游程检验

游程检验亦称“连贯检验”，是根据样本标志表现排列所形成的游程的多少进行判断的检验方法。游程检验是一种非参数性统计假设的检验方法，它是游程总数检验和最大游程检验的总称，用于两个独立样本的比较和观测结果随机性的检验测试。

游程检验检验问题可以表达为：

数据出现顺序随机数据出现顺序随机 $H_0$ 数据出现顺序随机⇔ $H_1$ 数据出现顺序随机

例2.6如在工厂的全面质量管理中,生产出来的20个工件的尺寸按顺序为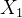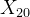（ $X_1$ ,…, $X_{20}$ )（单位cm）12.27、9.92、10.81、11.79、11.87、10.90、11.22、10.80、10.33、9.30、9.81、8.85、9.32、8.67、9.32、9.53、9.58、8.94、7.89、10.77人们想要知道生产出来的工件的尺寸变化是否只是由于随机因素，还是有其它非随机因素.

解题过程：

先找出它们的中位数为 $X_{med$ =9.865,再把大于 $X_{med$ 的记为1，小于的记为0,于是产生一串1和0：

1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 1

也就是说，变成了前面的情况.这时R=3，m=n=10而按照上面的公式（只要算两项）,P(R<=3) =P(R=2)+P(R=3)=0.00006即p值为0.0001.于是可以在水平a>0.0001时拒绝零假设.这里，算的是P(R<=3）而不是P(R>=3）是因为显然R=3离最小可能的值2要比最大可能的值20要近，因此可以说，在生产过程中有非随机因素起作用。

根据我们的R程序得到精确的双边检验的p值为0.00012，而相应的渐近的p值为0.00024.精确的p值和渐近p值差别较大，显然，这源于样本量不够大。

R代码：

run.test=function(y,cut=0){ if(cut!=0)x=(y>cut)*1 else x=y
N=length(x);k=1;for(i in 1:(N-1))if (x[i]!=x[i+1])k=k+1;r=k;
m=sum(1-x);n=N-m;
P1=function(m,n,k){
  2*choose(m-1,k-1)/choose(m+n,n)*choose(n-1,k-1)}
P2=function(m,n,k){choose(m-1,k-1)*choose(n-1,k)/choose(m+n,n)
  +choose(m-1,k)*choose(n-1,k-1)/choose(m+n,n)}
r2=floor(r/2);if(r2==r/2){pv=0;for(i in 1:r2) pv=pv+P1(m,n,i);
for(i in 1:(r2-1)) pv=pv+P2(m,n,i)} else {pv=0
for(i in 1:r2) pv=pv+P1(m,n,i)
for(i in 1:r2) pv=pv+P2(m,n,i)};if(r2==r/2)
  pv1=1-pv+P1(m,n,r2) else pv1=1-pv+P2(m,n,r2);
z=(r-2*m*n/N-1)/sqrt(2*m*n*(2*m*n-m-n)/(m+n)^2/(m+n-1));
ap1=pnorm(z);ap2=1-ap1;tpv=min(pv,pv1)*2;
list(m=m,n=n,N=N,R=r,Exact.pvalue1=pv,
     Exact.pvalue2=pv1,Aprox.pvalue1=ap1, Aprox.pvalue2=ap2,
     Exact.2sided.pvalue=tpv,Approx.2sided.pvalue=min(ap1,ap2)*2)}
x=c(12.27,9.92,10.81,11.79,11.87,10.90,11.22,10.80,10.33,9.30,9.81,8.85,9.32,8.67,9.32,9.53,9.58,8.94,7.89,10.77)
x=as.matrix(x)#设置成矩阵数据
y=factor(sign(x-median(x)));run.test(x>median(x))

代码运行结果：

标签：人工智能 r语言

本文转载自: https://blog.csdn.net/qq_58594320/article/details/128650471
版权归原作者 JIA...Thriteen 所有，如有侵权，请联系我们删除。

非参数检验之符号检验、Wilcoxon符号秩检验、游程检验

一、符号检验

例2.1下面是世界上71个大城市的花费指数(包括租金)按递增次序排列如下(这里上海是44位，其指数为63.5）：

R代码：

二、Wilcoxon符号秩检验

例2.3下面是10个欧洲城镇每人每年平均消费的酒类相当于纯酒精数（单位：升）.数据已经按照升幂排列.

R代码：

三、游程检验

R代码：

发表评论

“非参数检验之符号检验、Wilcoxon符号秩检验、游程检验”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航