卷进大厂系列之LeetCode刷题笔记：设计链表（中等）

学算法，刷力扣，加油卷，进大厂！

题目描述

力扣题目链接

设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性：val 和 next。val 是当前节点的值，next 是指向下一个节点的指针/引用。如果要使用双向链表，则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。

在链表类中实现这些功能：

• get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
• addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
• addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
• addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
• deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

示例：

MyLinkedList linkedList =newMyLinkedList();
linkedList.addAtHead(1);
linkedList.addAtTail(3);
linkedList.addAtIndex(1,2);//链表变为1-> 2-> 3
linkedList.get(1);//返回2
linkedList.deleteAtIndex(1);//现在链表是1-> 3
linkedList.get(1);//返回3

提示：

• 所有val值都在 [1, 1000] 之内。
• 操作次数将在 [1, 1000] 之内。
• 请不要使用内置的 LinkedList 库。

涉及算法

道题目属于中等题型，涉及到数据结构中的链表。这道题目呢，要求我们去根据要求设计链表，而不是单单让我们根据题目要求使用链表这个数据结构。那我们就要根据链表一些特性进行设计：

• 链表是由节点组成的，在链表的每个节点中，由两部分组成，即数据域（存放数据）和指针域（指向下一个节点的指针）；
• 链表不能像数组一样可以直接定位元素位置，因此它的查找比较慢；
• 链表的删除和添加都是直接通过指针来添加的，因此不存在像数组一样的覆盖，这样就快了很多（如下图）

单链表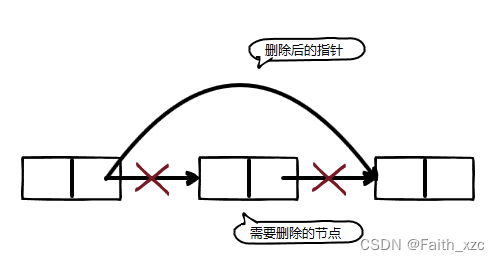

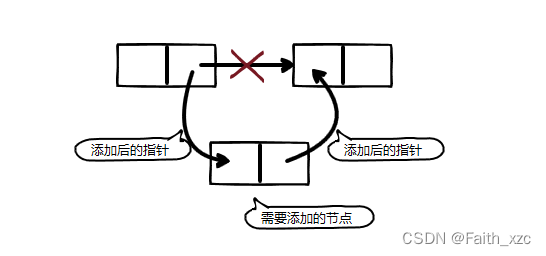
那么根据题目我们可以提炼出的关键点：

• 可以使用单链表或者双链表
• 单链表中的两个属性值，val 是当前节点的值，next 是指向下一个节点的指针/引用；双链表的话，在此基础上添加一个属性，prev 以指示链表中的上一个节点

解决这道题目呢，我们需要做的就是根据前面说到的链表的特性结合题目要求，设计链表类，然后实现指定的操作就可以了。（本文使用单链表实现，双链表后续补充）

题目解答

Java题解一

使用单链表

• 使用单链表的话，需要给MyLinkedList 类中，添加一个虚拟的头结点，这样的话，方便题目要求的在链表的第一个位置添加；
• 然后根据前面我们画的删除和添加的图发现，如果是删除元素，我们需要找到这个元素的前驱和后继节点；添加元素的话，需要根据其位置找到它的前驱节点和后继节点；
• 为了方便链表的查找，我们给MyLinkedList 类中设置一个size属性，表示存储链表元素的个数。

根据以上分析，实现代码如下：

//定义单链表类classListNode{int val;//当前节点的值ListNode next;//指向下一个节点的指针ListNode(){}ListNode(int val){this.val = val;}}classMyLinkedList{//size 存储链表元素的个数int size;//虚拟头结点ListNode head;//初始化链表publicMyLinkedList(){
        size =0;
        head =newListNode(0);}//获取第index节点的数值publicintget(int index){//如果index非法，返回-1if(index <0|| index >= size ){return-1;}//定义移动的节点ListNode curNode = head;//包含一个虚拟节点，所以查找第index +1 个节点for(int i =0; i <= index; i++){
            curNode = curNode.next;}return curNode.val;}//在链表最前面插入一个节点publicvoidaddAtHead(int val){addAtIndex(0,val);}//在链表最后面插入一个节点publicvoidaddAtTail(int val){addAtIndex(size,val);}publicvoidaddAtIndex(int index,int val){//排除index大于链表长和小于0的情况if(index > size ){return;}if(index <0){
            index =0;}//定义前驱节点ListNode pre = head;//链表长度加一++size;//循环查找直到indexfor(int i =0; i < index; i++){
            pre = pre.next;//往后查找}//定义插入的节点addListListNode addList =newListNode(val);//将节点插入
        addList.next = pre.next;
        pre.next = addList;}publicvoiddeleteAtIndex(int index){//排除index大于链表长和小于0的情况if(index >= size || index <0){return;}//定义前驱节点ListNode pre = head;//链表长度减一
        size--;//循环查找直到indexfor(int i =0; i < index; i++){
            pre = pre.next;//往后查找}//将节点删除
        pre.next = pre.next.next;}}

复杂度分析

时间复杂度：

• addAtHead： \O(1)
• addAtInder，get，deleteAtIndex: O(k)，其中 k 指的是元素的索引。
• addAtTail：O(N)，其中 N 指的是链表的元素个数。

空间复杂度：

• 所有的操作都是 O(1)。