摘要
继上周学习了贝叶斯基础的理论,本周将朴素贝叶斯和贝叶斯网络运用到实践中去,通过对代码的逐行分析,更加深入理解了贝叶斯。接着前两周提出“训练集达不到最优化”的问题,继续探究了批次、动量、学习率的影响因素。最终得出,小批次的数据集具有更高的精确度;动量可以解决局部最小值的困境;均方差和自适应学习率会使得学习率进行动态的改变,优化了学习率大不收敛和学习率小速度慢的问题。
Abstract
Following last week's study of the theory underlying Bayes, this week we put Simple Bayes and Bayesian Networks into practice, analyzing the code line by line to gain a deeper understanding of Bayes. After the problem of “training set is not optimized” raised in the previous two weeks, we continued to explore the influence of batch, momentum and learning rate. Finally, we concluded that small batch data sets have higher accuracy; momentum can solve the dilemma of local minima; mean squared deviation and adaptive learning rate can make the learning rate change dynamically, which optimizes the problem of non-convergence for large learning rate and slow speed for small learning rate.
一、贝叶斯理论的代码实践
1、朴素贝叶斯
step1 创建数据集
x1 = [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3]
x2 = ['S','M','M','S','S','S','M','M','L','L','L','M','M','L','L']
y = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1]
df = pd.DataFrame({'x1':x1, 'x2':x2, 'y':y})
print(df.head())
X = df[['x1', 'x2']]
y = df[['y']]
print(X.head())
print(y.head())
x1、x2是两类不同的特征,每个特征中含有相同或不同的表现;y是代表类别,该例中分为1、-1两个类别。利用dataframe的数据结构使数据排列成表格的样式。 需要提前导入numpy和pandas库。
NumPy主要用于处理数值数据,提供了ndarray数组来容纳数据,支持并行计算,底层使用C语言编写,效率高。Pandas主要用于处理类表格数据,提供了Series和DataFrame数据结构。NumPy适合处理统一的数组数据,而Pandas更适合处理结构化数据。
运行结果如下:
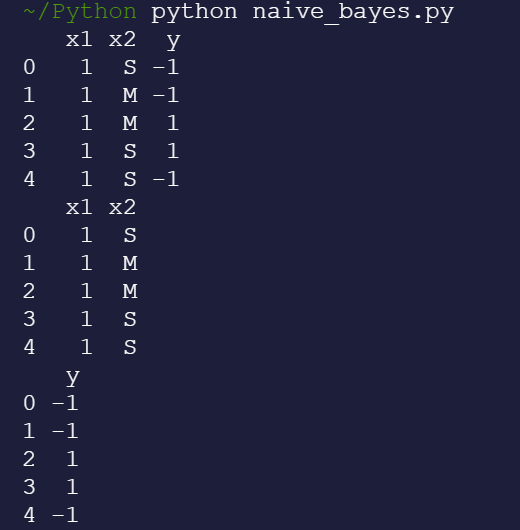
利用head()方法打印出表格的前五行。
step2 朴素贝叶斯计算概率
def nb_fit(X, y):
classes = y[y.columns[0]].unique() #挑出所有类别
class_count = y[y.columns[0]].value_counts() #统计每种类别所含数目
class_prior = class_count / len(y) #计算处每种类别在所有样本中占的几率,也就是类先验概率
print(class_count)
print(class_prior)
prior = dict()
for col in X.columns: #依次取出x1、x2的那一列
for j in classes: #依次取出1、-1两种类别
p_x_y = X[(y == j).values][col].value_counts() #不同类别中x1、x2的各个相同特征的统计
for i in p_x_y.index:
prior[(col, i, j)] = p_x_y[i] / class_count[j] #每个类别中该特征出现的概率,也就是似然条件概率
return classes, class_prior, prior
classes, class_prior, prior = nb_fit(X, y)
print(classes) #类别
print(class_prior)#类先验概率
print(prior) #条件概率
由贝叶斯定理的公式可知,想要计算出类后验概率,来将含有多个特征的物体分到概率较大的类别中, 就需要提前计算出类先验概率class_prior和条件概率prior。朴素贝叶斯可以假设各个特征之间相互独立,所以可以简化计算,省去计算全概率的步骤。(理论见周报四:CSDN)
运行结果如下:
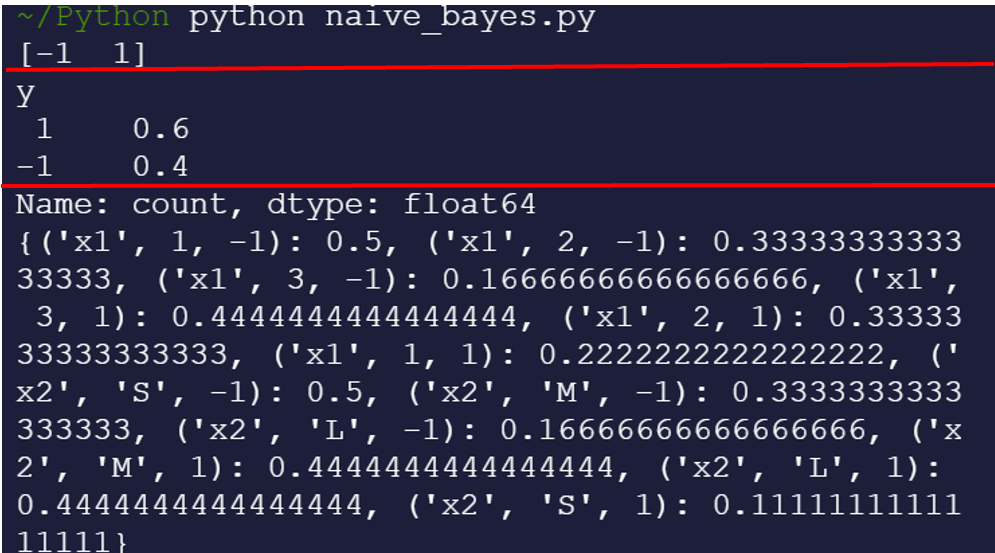
以红线划分,第一格是类别,第二格是手动统计出来的类先验概率,第三格是每一种特征的不同表现在两个类别中分别的发生概率(条件概率)。
step3 根据训练集来预测新的数据
X_test = {'x1': 2, 'x2': 'S'}
def predict(X_test):
res = []
for c in classes:
p_y = class_prior[c]#类先验概率
p_x_y = 1
for i in X_test.items():
p_x_y *= prior[tuple(list(i)+[c])] #条件概率(所有特征的条件概率依次相乘)
res.append(p_y*p_x_y)#用连乘的方式计算每个类别的后验概率的简化h1、h2(类先验概率和条件概率的乘积,忽略总概率)
return classes[np.argmax(res)] #选取概率值最大的类别
print('测试数据预测类别为:', predict(X_test))
我们把得到的类先验概率和各个特征的条件概率带入朴素贝叶斯公式中去,从而得到预测类别。
运行结果如下:

2、贝叶斯网络
一般来说,现实情况较复杂,特征多且之间存在着千丝万缕的关系,所以朴素贝叶斯满足不了,进而提出了贝叶斯网络。
step1 建立网络结构
from pgmpy.factors.discrete import TabularCPD
from pgmpy.models import BayesianModel
letter_model = BayesianModel([('D', 'G'),
('I', 'G'),
('G', 'L'),
('I', 'S')])
网络结构如下图:
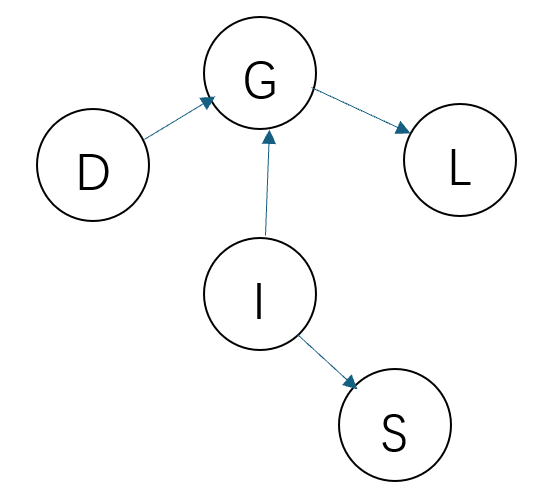
其中G是学生成绩、D是考试难度、L是推荐信质量、I是个人天赋、S是SAT考试分数。
step2 填入节点参数
# 学生成绩的条件概率分布
grade_cpd = TabularCPD(
variable='G', # 节点名称
variable_card=3, # 节点取值个数
values=[[0.3, 0.05, 0.9, 0.5], # 该节点的概率表
[0.4, 0.25, 0.08, 0.3],
[0.3, 0.7, 0.02, 0.2]],
evidence=['I', 'D'], # 该节点的依赖节点
evidence_card=[2, 2] # 依赖节点的取值个数
)
print(grade_cpd)
运行结果如下 :

可以看出,学生成绩的依赖G分别是个人天赋I和考试难度D。该条件概率分布表中,学生成绩分为G(0)、G(1)、G(2)三个等级,在“个人天赋好或坏”和在“考试难度高或低”的四种交叉情况下,学生成绩达到不同等级的概率。
剩余的四个节点D、L、I、S如上写法填入参数 difficulty_cpd,intel_cpd,letter_cpd, sat_cpd。
step3 节点加入到模型中
# 将各节点添加到模型中,构建贝叶斯网络
letter_model.add_cpds(
grade_cpd,
difficulty_cpd,
intel_cpd,
letter_cpd,
sat_cpd
)
** step4 推理预测**
# 导入pgmpy贝叶斯推断模块
from pgmpy.inference import VariableElimination
# 贝叶斯网络推断
letter_infer = VariableElimination(letter_model)
# 天赋较好且考试不难的情况下推断该学生获得成绩等级
prob_G = letter_infer.query(
variables=['G'],
evidence={'I': 1, 'D': 0})
print(prob_G)
运行结果如下:
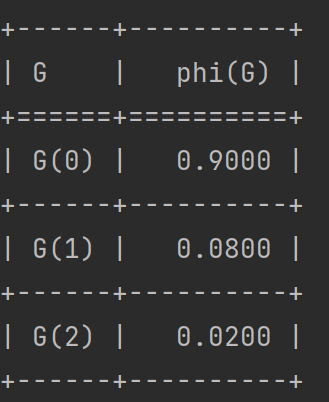
代码参考:Machine_Learning_Code_Implementation/charpter21_Bayesian_models/naive_bayes.ipynb at master · luwill/Machine_Learning_Code_Implementation · GitHub
报错:pgmpy已经安装好,但是并不能正常运行
解决:查看所有依赖包都安装好,未解决;python版本过高,应在3.7.x的版本,解决!
参考文章:【Python】pgmpy模块安装教程_pgmpy安装-CSDN博客
二、训练效果不好的解决方式
1、批次batch
取极端的两种情况如下:(左图为不分batch,右图为每个数据分为1个batch)

左图中整个数据集为1个batch,说明要updateN次,所有数据过完一遍后epoch1次;右图中数据集划分为N个batch,说明每个batch都要update1个数据,然后再epoch1次,总共update和epoch次数都为N。 可以看出,虽然largest batch中只epoch1次,但是效果比较显著;smallest batch中不停进行epoch,导致其每一轮的效果都不太明显,但是最终更加接近global minima。
batch size的大小影响着update、epoch的速度,进而影响了数据集训练的精确度,update、epoch和batch的关系经实验验证如下所示:

batch size设置越大,一个batch中所含数据数越多,所划分的batch个数越少,epoch的次数越少。
一个batch训练完update一次,那么batch size越大,按理update的速度越慢(batch size较小的时候,GPU的并行计算可以将其update的速度差别忽略不计);
所有batch训练完epoch一次,那么batch越少,按理epoch的速度越快(batch size较大的时候,epoch次数较小,GPU的并行计算仍然可以使epoch速度保持平稳)。
在实践中得到,small batch能够得到更大的精确度,如下:

出现这种情况的原因如下:

如果是large batch,那么只有一条梯度下降的路线,选择比较少,若是遇到local minima的情况就会导致optimization fail;如果是small batch,那么会有更多的batch,那么梯度下降的曲线就比较多,stuck的情况较少。
small batch v.s. large batch

由上图总结可以看出,small和large在不同情况下各有优势,总体来看还是small batch更优一点。
2、动量mometum
从物理学的角度来看,小球在走到local minima的时候,有可能还存在动量使小球翻过local minima从而不会出现stuck的情况。如下:

所以,提出了momentum融入gradient descent的方法,如下例所示:

该例中梯度下降的方向正好是gradient的反方向,动量是根据前面的gradient所计算得到的,最终每一次移动的方向都是gradient和movement的大小方向的向量和。其计算步骤总结如下:

3、学习率learning rate
有时候会出现stuck的情况,并不一定是达到了gradient接近零的情况(极值点),而是可能会出现震荡如下:
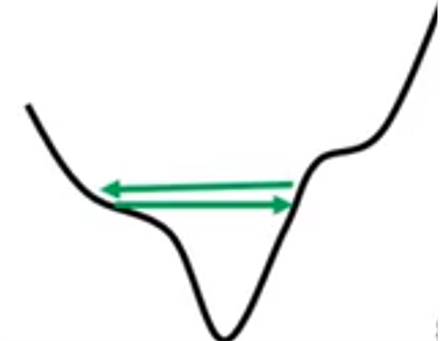
这样来回到达不了global minima无法使训练停止,原因是学习率设置不当。
上图中学习率过大,导致震荡,无法收敛;但如果学习率过小,会导致梯度下降缓慢,训练时间过长。所以,根据经验可得,学习率应该根据不同情况来动态调整。
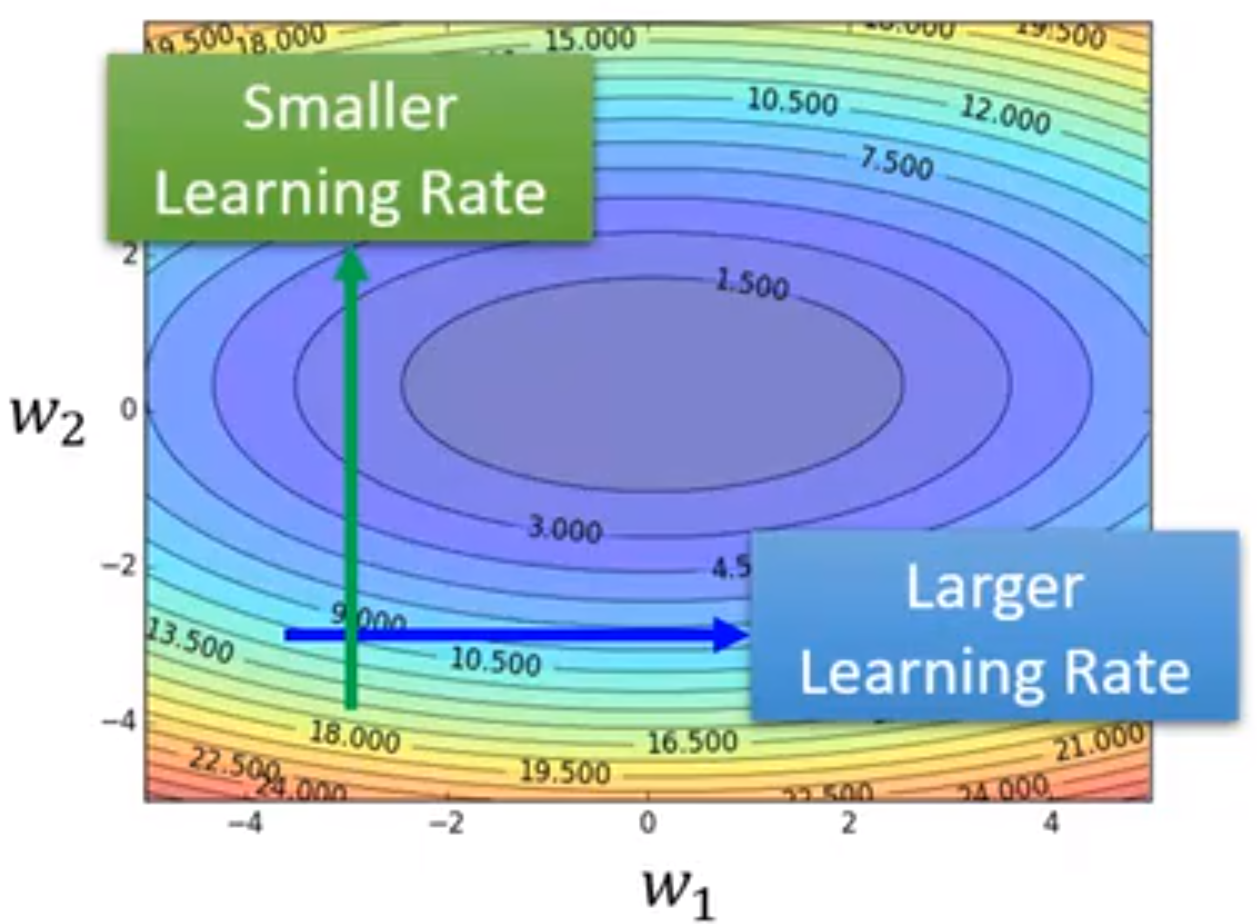
应该在梯度较小(平坦)的地方设置lager学习率,在梯度较大(陡峭)的地方设置smaller学习率。所以学习率是动态变化的,需要均方根计算,如下:

如果想要在同一方向上实现不同的学习率,那么需要用到自适应学习率RMSProp
RMSProp:一种自适应学习率的优化算法。它通过计算梯度平方的移动平均值来调整学习率,从而为每个参数提供不同的学习率,并在训练过程中自适应地调整。 核心思想是利用历史梯度的指数衰减平均来自适应地调整学习率。
下周继续学习learning rate的内容,Adam、learning rate scheduling等
总结
本周解决了前两周遗留的问题,对贝叶斯理论的理解更加深刻,进一步讨论了optimization fail的影响因素。下周将继续完成“学习率”部分,并且继续了解损失函数对optimization fail的影响及解决方案。
版权归原作者 本本的小橙子 所有, 如有侵权,请联系我们删除。