目录
参考学习b站资源:
数学建模学习交流
bp神经网络预测matlab代码实现过程
神经网络简介
1.项目源码
可在github下载(含原始样品数据):
https://github.com/chenshunpeng/BP-neural-network
2.神经网络介绍
最早的神经网络模型, 单层感知器perceptron,结构如下:
这是一个两层的神经网络,第一层为输入层,第二层为输出层。因为只有在输出层需要进行计算,就是说只有一层计算层,所以称之为单层感知器。从形式上看,仅仅是将MP模型中的输入信号当作了独立的一层神经元,但是本质上却有很大差别。
感知器模型中权重和阈值不再是固定的了,而是计算机"学习"出来的结果。引入了损失函数的概念,通过迭代不断调整权重和阈值,使得损失函数最小,以此来寻找最佳的权重和阈值。
单层感知器只可以解决线性可分的问题,在单层感知器的基础上,再引入一层神经元,构成一个2层的神经网络(要刨去输入层),结构如下: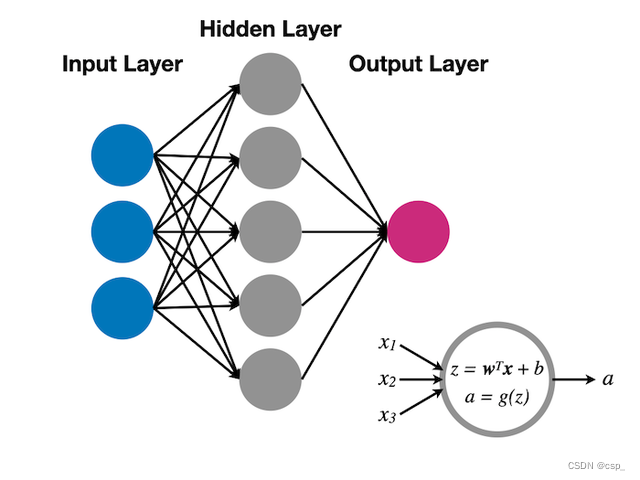
这样的一个神经网络模型,适用范围更广,涵盖了线性和非线性可分的场景。其中的每一层称之为layer, 除了输出层和输出层之外,还有中间的隐藏层。这样的神经网络模型,通过反向传播算法来求解。
增加一层的好处在于更好的数据表示和函数拟合的能力,在3层的基础上,再引入更多的隐藏层,就变成了深度神经网络,图示如下: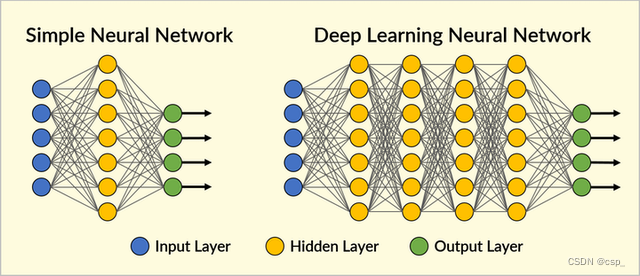
可以看到,每增加一层,模型的参数数量急剧增加,所以深度学习对计算资源的要求特别高,在实际使用中,模型训练时间非常的久。
虽然耗费计算资源,但是深度学习的优点也很突出,相比机器学习,模型自动完成特征提取,不需要人工的特征工程,这一点对于高维数据的处理特别重要
3.辛烷值的预测
【改编】辛烷值是汽油最重要的品质指标,传统的实验室检测方法存在样品用量大,测试周期长和费用高等问题,不适用于生产控制,特别是在线测试。近年发展起来的近红外光谱分析方法(NIR),作为一种快速分析方法,已广泛应用于农业、制药、生物化工、石油产品等领域。其优越性是无损检测、低成本、无污染,能在线分析,更适合于生产和控制的需要。
实验采集得到50组汽油样品(辛烷值已通过其他方法测量),并利用傅里叶近红外变换光谱仪对其进行扫描,扫描范围900~1700nm,扫描间隔为2nm,即每个样品的光谱曲线共含401个波长点,每个波长点对应一个吸光度。
- 请利用这50组样品的数据,建立这401个吸光度和辛烷值之间的模型。
- 现给你10组新的样本,这10组样本均已经过近红外变换光谱仪扫描,请预测这10组新样本的辛烷值。
Excel截图: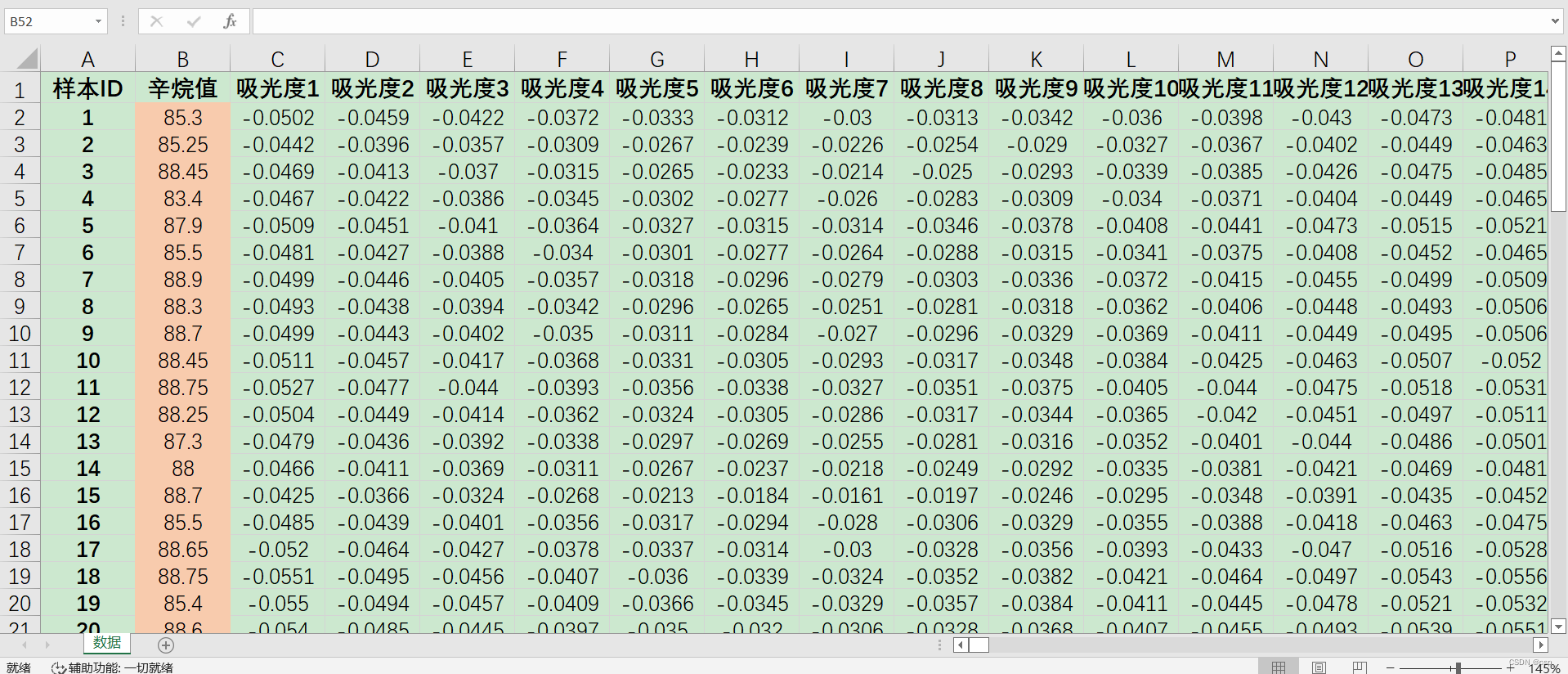
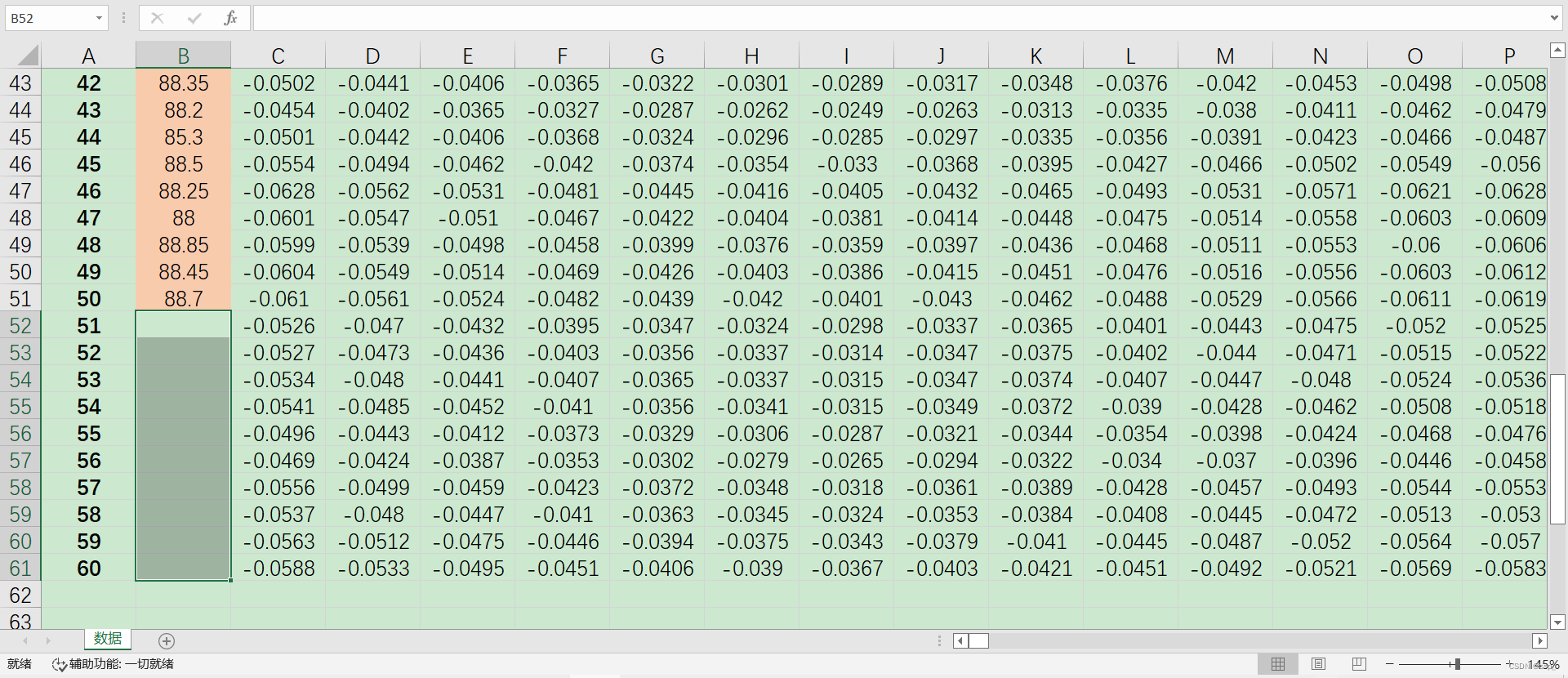
3.1.原始样品数据
因为数据太多,博客只放了一部分,完整Excel可以在github项目中下载:
https://github.com/chenshunpeng/BP-neural-network
首先导入数据:
new_X:需要预测的输入层数据
X:样品的输入层数据
Y:样品的输出层数据
3.2.matlab代码实现
%% 此程序为matlab编程实现的BP神经网络
% 清空环境变量
% clear
close all %关闭所有图形窗口
clc
%%第一步 读取数据
input=X;%载入输入数据
output=Y;%载入输出数据
%% 第二步 设置训练数据和预测数据
% 注意要将指标变为列向量
input_train =input(1:40,:)';
output_train =output(1:40,:)';
input_test =input(41:50,:)';
output_test =output(41:50,:)';%节点个数
inputnum=401;% 输入层节点数量
hiddennum=10;% 隐含层节点数量
outputnum=1;% 输出层节点数量
%% 第三本 训练样本数据归一化
[inputn,inputps]=mapminmax(input_train);%归一化到[-1,1]之间,inputps用来作下一次同样的归一化
[outputn,outputps]=mapminmax(output_train);%% 第四步 构建BP神经网络
net=newff(inputn,outputn,hiddennum,{'tansig','purelin'},'trainlm');% 建立模型,传递函数使用purelin,采用梯度下降法训练
W1= net. iw{1,1};%输入层到中间层的权值
B1= net.b{1};%中间各层神经元阈值
W2= net.lw{2,1};%中间层到输出层的权值
B2= net. b{2};%输出层各神经元阈值
%% 第五步 网络参数配置( 训练次数,学习速率,训练目标最小误差等)
net.trainParam.epochs=1000;% 训练次数,这里设置为1000次
net.trainParam.lr=0.01;% 学习速率,这里设置为0.01
net.trainParam.goal=0.00001;% 训练目标最小误差,这里设置为0.00001%% 第六步 BP神经网络训练
net=train(net,inputn,outputn);%开始训练,其中inputn,outputn分别为输入输出样本
%% 第七步 测试样本归一化
inputn_test=mapminmax('apply',input_test,inputps);% 对样本数据进行归一化
%% 第八步 BP神经网络预测
an=sim(net,inputn_test);%用训练好的模型进行仿真
%% 第九步 预测结果反归一化与误差计算
test_simu=mapminmax('reverse',an,outputps);%把仿真得到的数据还原为原始的数量级
error=test_simu-output_test;%预测值和真实值的误差
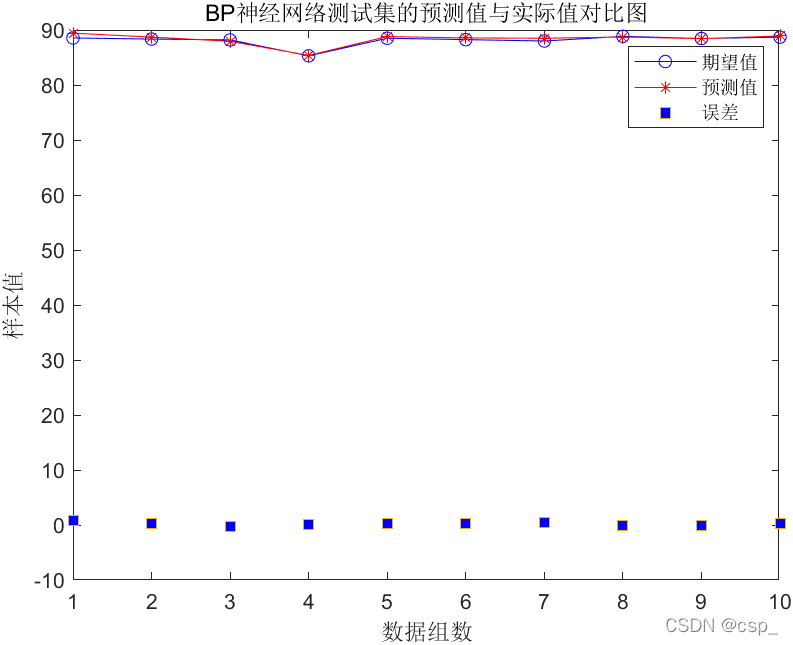
%%第十步 真实值与预测值误差比较
figure('units','normalized','position',[0.1190.20.380.5])plot(output_test,'bo-')
hold on
plot(test_simu,'r*-')
hold on
plot(error,'square','MarkerFaceColor','b')legend('期望值','预测值','误差')xlabel('数据组数')ylabel('样本值')title('BP神经网络测试集的预测值与实际值对比图')[c,l]=size(output_test);MAE1=sum(abs(error))/l;MSE1=error*error'/l;RMSE1=MSE1^(1/2);disp(['-----------------------误差计算--------------------------'])disp(['隐含层节点数为',num2str(hiddennum),'时的误差结果如下:'])disp(['平均绝对误差MAE为:',num2str(MAE1)])disp(['均方误差MSE为: ',num2str(MSE1)])disp(['均方根误差RMSE为: ',num2str(RMSE1)])
关于隐含层数的确定(这里是10),需要注意的是:
- 如果不用公式的话,可以逐步试验得到隐层节点数,就是先设置一个初始值,然后在这个值的基础上逐渐增加,比较每次网络的预测性能,选择性能最好的对应的节点数作为隐含层神经元节点数(逐步增加是因为确定隐含层节点数的基本原则是:在满足精度的前提下,取尽可能紧凑的结构,即取尽可能少的隐含层节点数)
- 如果用公式的话,一般有几个经验公式(建议了解一下神经网络的数学/理论部分),带入看哪个效果好,就取哪个为基准,再结合逐步试验法确定隐层节点数,但因为权值和阈值是每训练一次,调整一次,所以只能尽量趋于最优(好像也可以通过遗传算法、粒子群算法这样的优化算法来确定,就比较高深了)
训练结果:
-----------------------误差计算--------------------------
隐含层节点数为10时的误差结果如下:
平均绝对误差MAE为:0.30444
均方误差MSE为: 0.14714
均方根误差RMSE为: 0.38359
进行预测:
predict_y =zeros(10,1);% 初始化predict_y
pre_test=mapminmax('apply',new_X(:,:)',inputps);% 对预测数据进行归一化
for i =1:10
result =sim(net,pre_test(:,i));predict_y(i)= result;
end
disp('预测值为:')
predict_y=mapminmax('reverse',predict_y,outputps);%把预测结果还原
disp(predict_y)
结果:
预测值为:
87.963387.858188.806785.466685.315583.100586.326686.710689.194087.0632
需要注意的是,不同的神经网络模型参数会对预测值有影响,比如隐含层的个数(默认为10),测试集比例,训练方法等,另一方面,样本数量的局限或是模型的质量也都有可能对结果有很大的影响
3.3.工具箱实现
3.3.1.莱文贝格-马夸特方法
在Matlab的菜单栏点击APP,再点击Neural Fitting app(神经网络工具箱):
注意到左下角有一个模块:
点击后出现:
我们可以在这里看到对它的介绍:
可以简单了解一下:
之后接着进行操作:
注意选择样本在行上面(Matrix rows),也就是说每一行对应一个样本的所有数据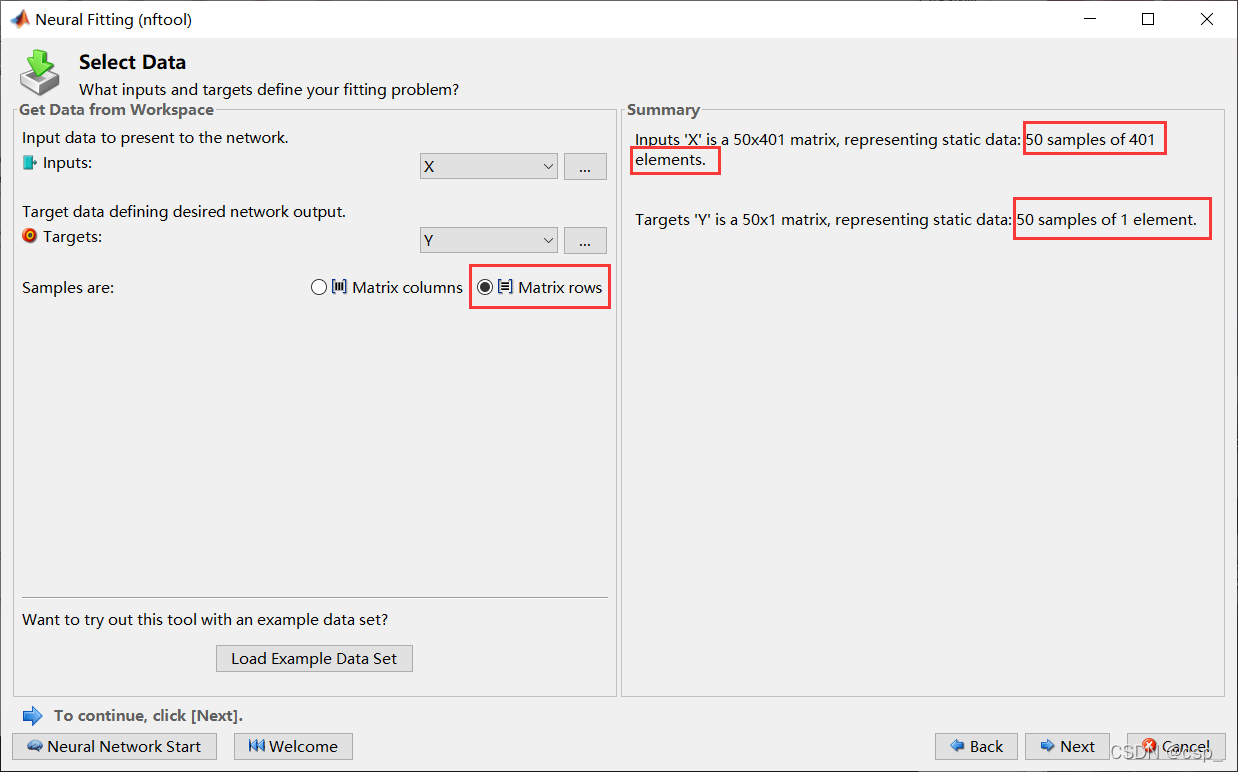
之后出现: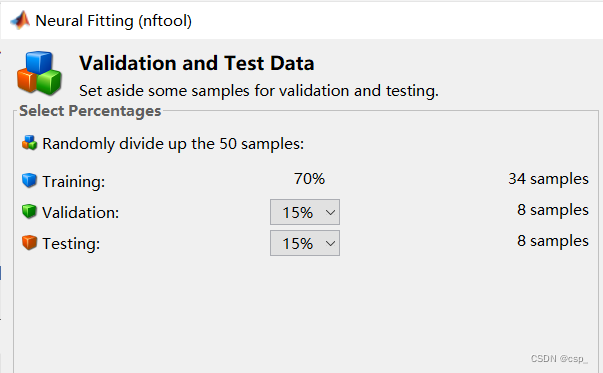
解释:
训练集(Training set) —— 用于模型拟合的数据样本。
验证集(Validation set)—— 是模型训练过程中单独留出的样本集,它可以用于调整模型的超参数和用于对模型的能力进行初步评估。在神经网络中,我们用验证数据集去寻找最优的网络深度,或者决定反向传播算法的停止点或者在神经网络中选择隐藏层神经元的数量;
测试集(Testing set) —— 用来评估模最终模型的泛化能力。但不能作为调参、选择特征等算法相关的选择的依据。
之后默认选择隐含层的个数为10(就是说有10个神经元进行预测,即output部分有10个):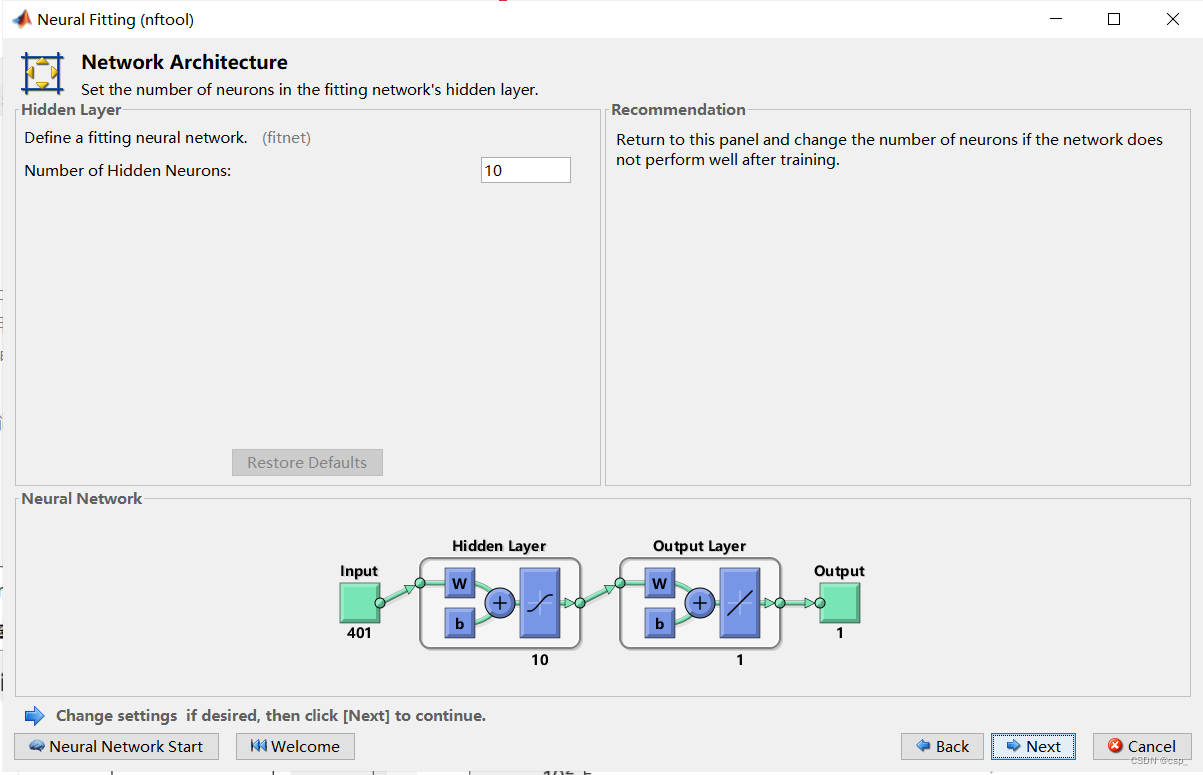
之后选择训练方法:
解释:
三种训练方法:
莱文贝格-马夸特方法(Levenberg–Marquardt algorithm)
贝叶斯正则化方法(Bayesian‐regularization)
量化共轭梯度法(Scaled Conjugate Gradient )
选择合适的进行训练即可
训练结果:
在时刻9(训练了9次)验证集valiadation出现了最低的均方误差,选择时刻9的模型为最佳模型:
横坐标:训练结束时的epochs数(神经网络一次前向传播+一次反向传播=一个epoch)
纵坐标:均方误差
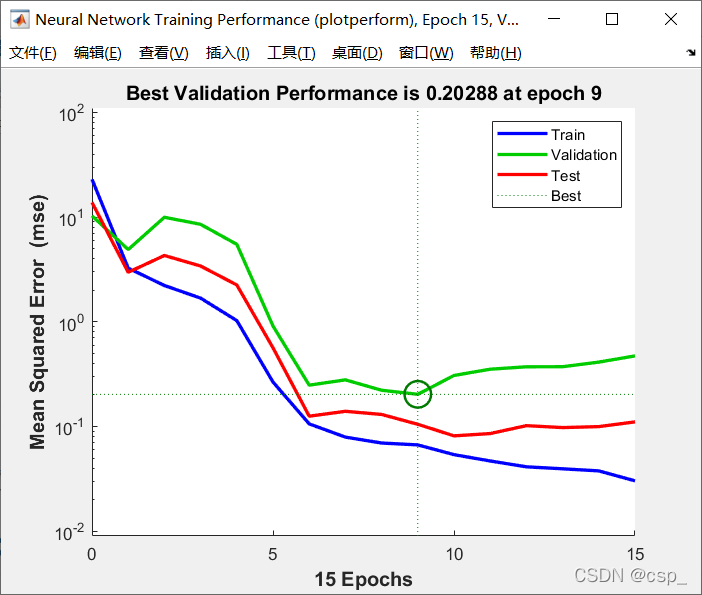
这三条线分别是:训练集(train)、验证集(validation)和测试集(test)
训练集(蓝线所用数据集):训练模型,得到模型参数
验证集(绿线所用数据集):评估模型,得到的最优网络
测试集(红线所用数据集):用之前得到的最优网络来评估模最终模型的泛化能力
解释一下为什么最佳模型的标注在绿线上:
首先使用训练集训练多个网络模型(假设为t1,t2,t3 … tn),再使用验证集测试这些网络,找到得分最高的那个网络(假设为t9)作为我们选择的最佳网络,所以最佳模型的标注在绿线上,红线则是网络模型将训练集和验证集合并训练而产生的(其实,绿线类似Kaggle中的Private Testing Set)
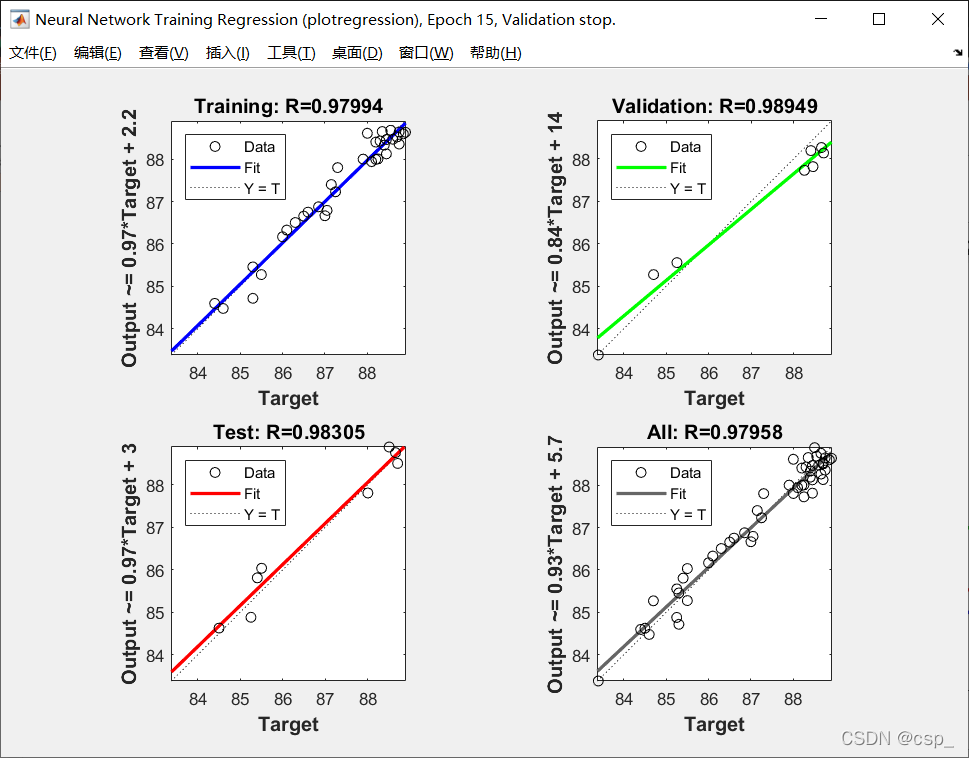
将拟合值对真实值回归,拟合优度越高,说明拟合的的效果越好:
对应的神经网络图: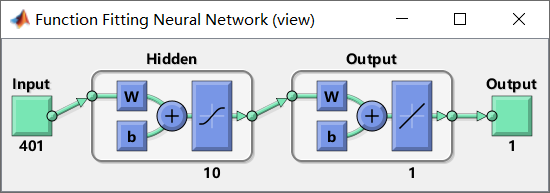
最后保存训练出来的神经网络模型:
其中 net 即训练出来的神经网络模型
进行预测:
% 写一个循环,预测接下来的十个样本的辛烷值
% 注意要将指标变为列向量,然后再用sim函数预测
predict_y =zeros(10,1);% 初始化predict_y
for i =1:10
result =sim(net,new_X(i,:)');predict_y(i)= result;
end
disp('预测值为:')disp(predict_y)
结果:
预测值为:
87.354787.123988.119484.995884.579685.427587.898686.492189.048387.4444
3.3.2.贝叶斯正则化方法
之后我们换一种训练方法(从 莱文贝格-马夸特方法 换到 贝叶斯正则化方法),发现训练了391次还没有结束,于是我就手动停止了(训练了长达19min):
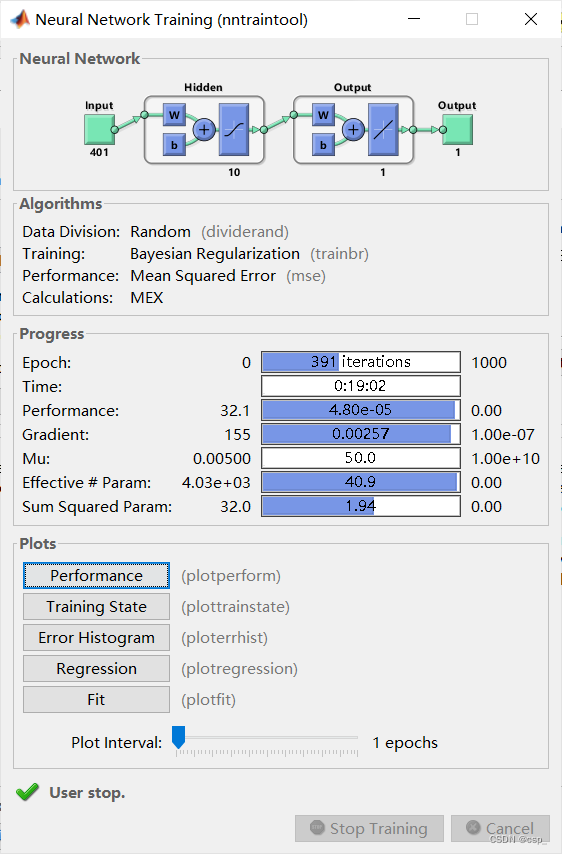
我们点击 (trainbr) 可以看到对贝叶斯正则化方法的详细介绍,及其局限性:
该函数使用雅可比矩阵进行计算,该函数假设性能是误差的平均值或平方和。
因此,使用该函数训练的网络必须使用mse或sse性能函数。
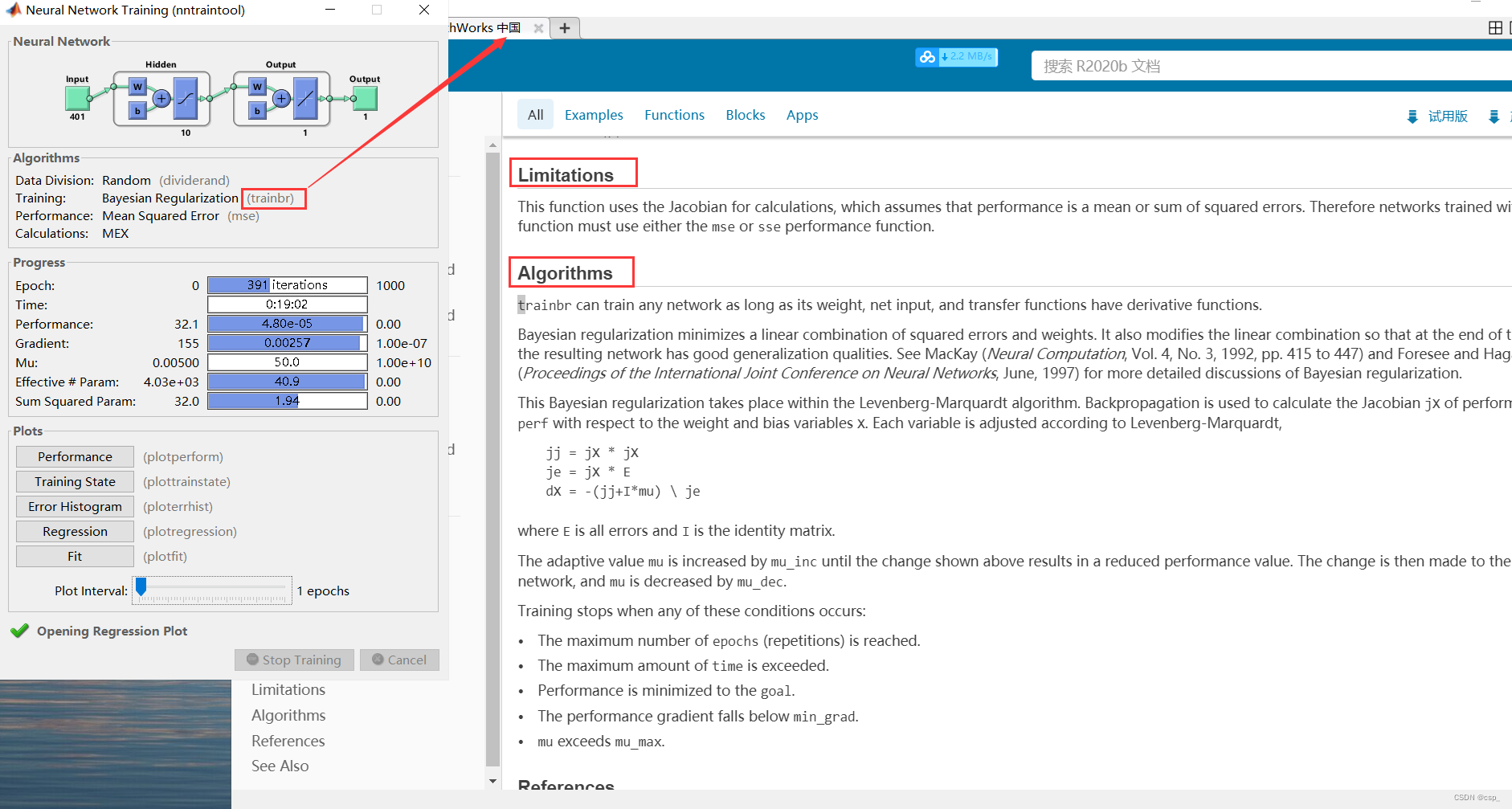
我们看训练的表现:
训练的MSE图(左图),回归图(右图):
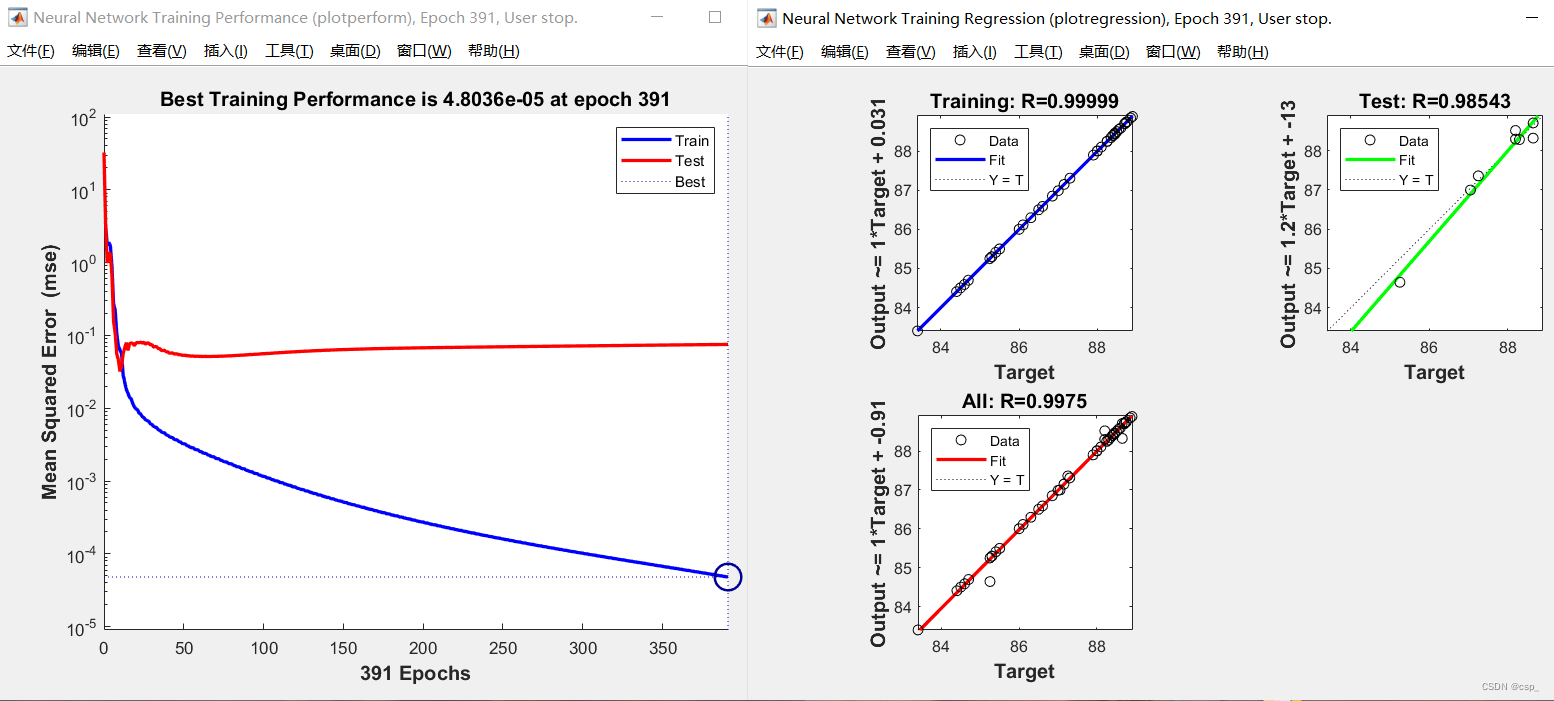
MSE图(左图)
横坐标: 训练结束时的epochs数【神经网络一次前向传播+一次反向传播=一个epoch】
纵坐标: 均方误差
从图中可以发现训练集最小均方误差一直在变小,测试集略微轻微增大,趋于稳定(但误差其实都已经非常非常小了)
回归图(右图)
横坐标: 样本原目标值
纵坐标: 神经网络输出预测值
可以得到原目标值和预测值的相关度;用系数R表示,若R越接近1,则表示线性化程度越高,结果越好
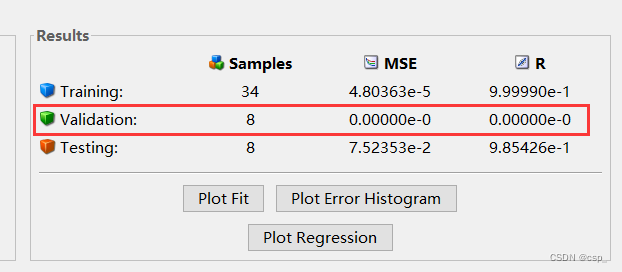
我们惊奇的发现没有
validation
,训检查了一下训练集(train)、验证集(validation)和测试集(test)在matlab工具箱中分别是70%,15%,15%的比例,没有问题,仔细看了一下原来是因为均方误差MSE和R指标在精度范围内已经为0,所以都不需要考虑它了!
训练的状态图(左图),误差直方图(右图):
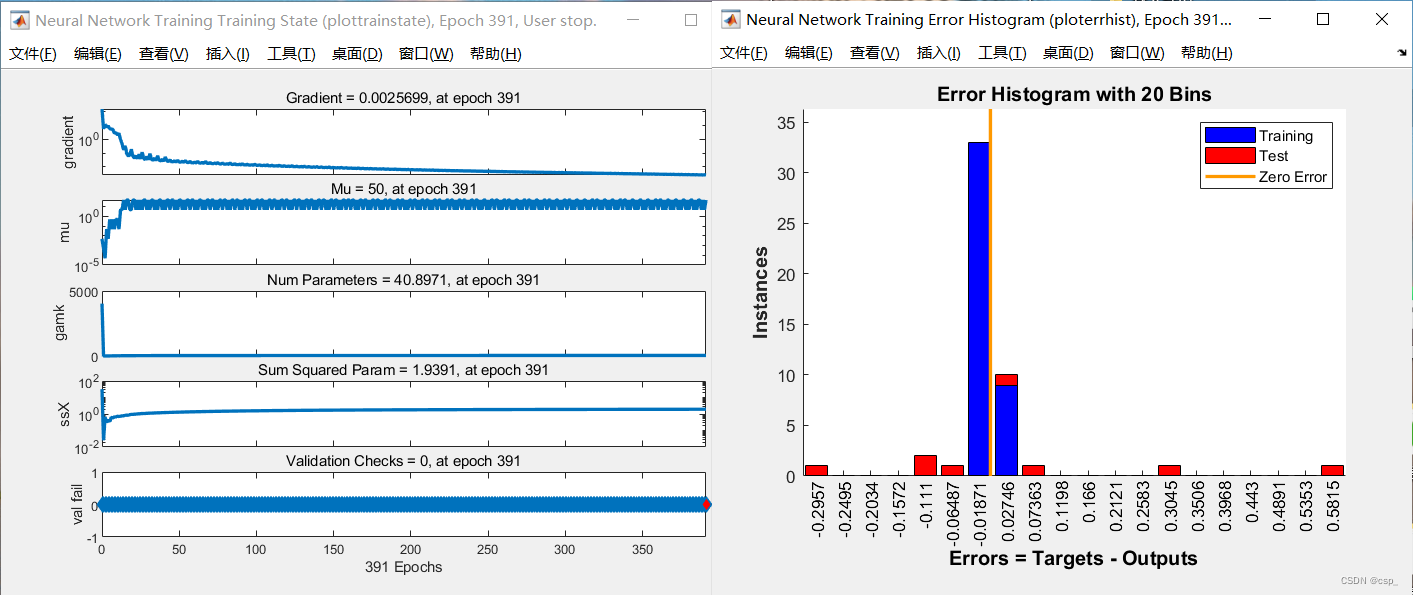
状态图(左图)
可以观察网络训练状态,判断是否终止训练
横坐标: epoch
纵坐标:
gradient:梯度,若梯度为0,则为图像最低点,即最优位置
mu:超参数
μ
\mu
μ(具体待研究)
val fail:可以理解为误差值(具体待研究)
validation check=0, at epoch 391
:代表到第391次训练时,训练误差的 连续增大epoch数 为0(其实就是第390次训练时训练误差比第391次大),设置
validation checks
是为了防止被训练的网络过拟合的
状态图的详细介绍可看帮助文档:
误差直方图(右图)
可以得到神经网络的输出值与样本原目标值的误差
横坐标: 误差区间的中位数;
纵坐标: 位于该误差区间的样本个数
之后可以通过这2个看训练的matlab代码:
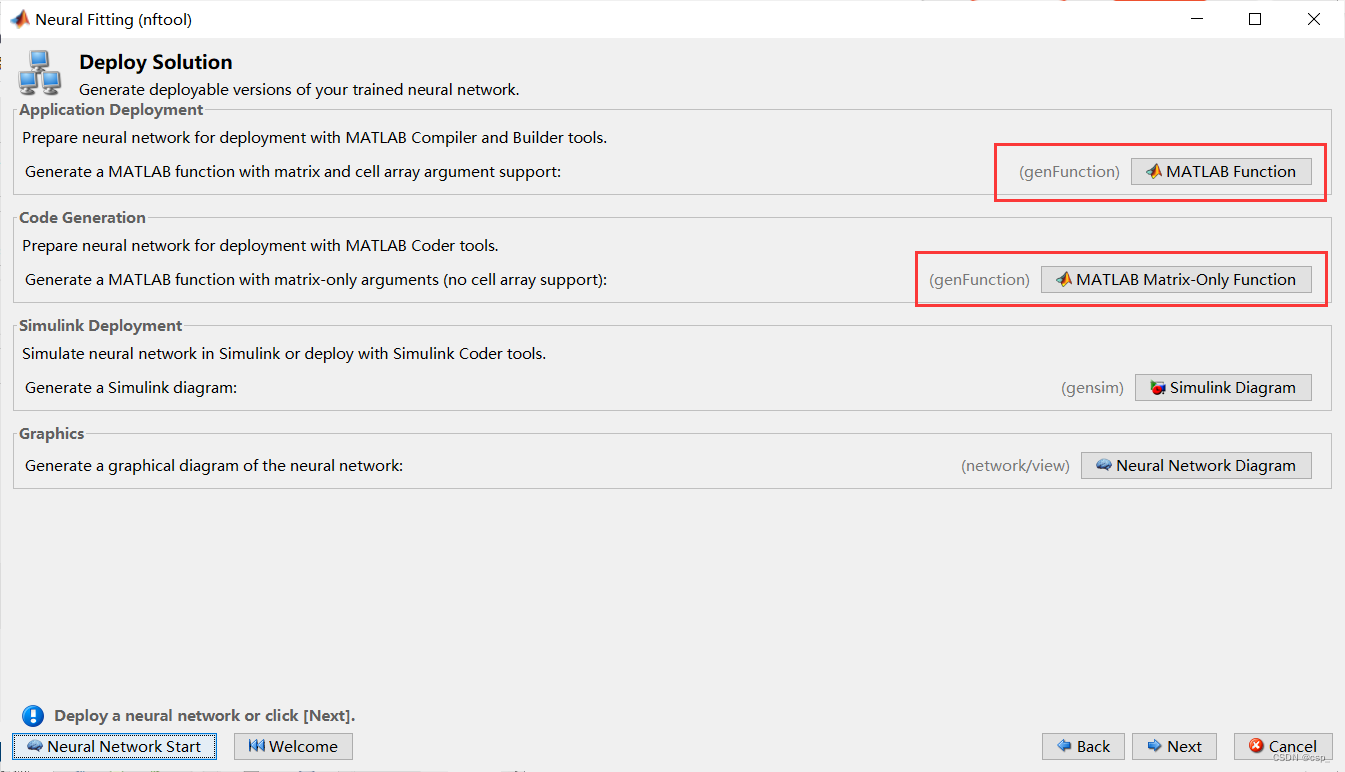
可以在这里体验神经网络的模拟部署:

大概是这样(具体功能可以自己了解)
可以看到神经网络图:

如下:
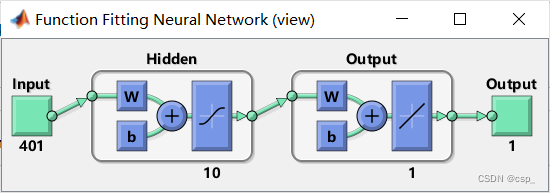
我们可以生成脚本,方便以后解决相同的问题:
代码:
% Solve an Input-Output Fitting problem with a Neural Network
% Script generated by Neural Fitting app
% Created 23-Jul-202219:10:11%% This script assumes these variables are defined:%%X- input data.%Y- target data.
x =X';
t =Y';% Choose a Training Function% For a list of all training functions type: help nntrain
%'trainlm'is usually fastest.%'trainbr' takes longer but may be better for challenging problems.%'trainscg' uses less memory. Suitable in low memory situations.
trainFcn ='trainbr';% Bayesian Regularization backpropagation.% Create a Fitting Network
hiddenLayerSize =10;
net =fitnet(hiddenLayerSize,trainFcn);% Choose Input and Output Pre/Post-Processing Functions
% For a list of all processing functions type: help nnprocess
net.input.processFcns ={'removeconstantrows','mapminmax'};
net.output.processFcns ={'removeconstantrows','mapminmax'};% Setup Division of Data for Training, Validation, Testing
% For a list of all data division functions type: help nndivision
net.divideFcn ='dividerand';% Divide data randomly
net.divideMode ='sample';% Divide up every sample
net.divideParam.trainRatio =70/100;
net.divideParam.valRatio =15/100;
net.divideParam.testRatio =15/100;% Choose a Performance Function% For a list of all performance functions type: help nnperformance
net.performFcn ='mse';% Mean Squared Error
% Choose Plot Functions
% For a list of all plot functions type: help nnplot
net.plotFcns ={'plotperform','plottrainstate','ploterrhist',...'plotregression','plotfit'};% Train the Network
[net,tr]=train(net,x,t);% Test the Network
y =net(x);
e =gsubtract(t,y);
performance =perform(net,t,y)% Recalculate Training, Validation and Test Performance
trainTargets = t .* tr.trainMask{1};
valTargets = t .* tr.valMask{1};
testTargets = t .* tr.testMask{1};
trainPerformance =perform(net,trainTargets,y)
valPerformance =perform(net,valTargets,y)
testPerformance =perform(net,testTargets,y)% View the Network
view(net)% Plots
% Uncomment these lines to enable various plots.%figure,plotperform(tr)%figure,plottrainstate(tr)%figure,ploterrhist(e)%figure,plotregression(t,y)%figure,plotfit(net,x,t)% Deployment
% Change the(false) values to(true) to enable the following code blocks.% See the help for each generation functionfor more information.if(false)% Generate MATLABfunctionfor neural network for application
% deployment inMATLAB scripts or withMATLAB Compiler and Builder
% tools, or simply to examine the calculations your trained neural
% network performs.genFunction(net,'myNeuralNetworkFunction');
y =myNeuralNetworkFunction(x);
end
if(false)% Generate a matrix-only MATLABfunctionfor neural network code
% generation withMATLAB Coder tools.genFunction(net,'myNeuralNetworkFunction','MatrixOnly','yes');
y =myNeuralNetworkFunction(x);
end
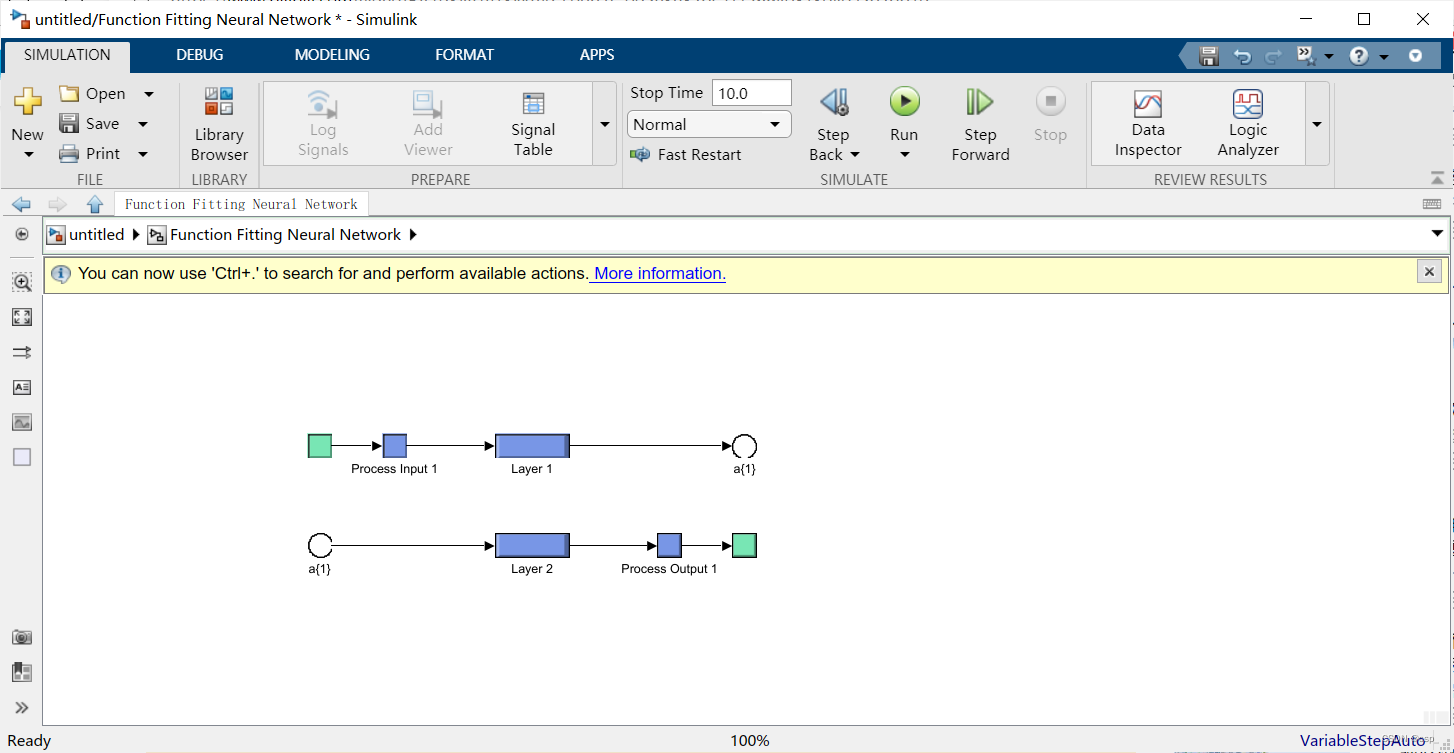
if(false)% Generate a Simulink diagram for simulation or deployment with.% Simulink Coder tools.gensim(net);
end
之后保存数据:
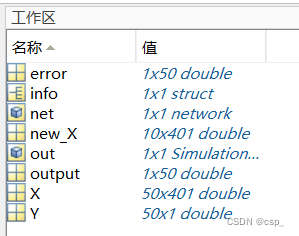
进行预测:
% 写一个循环,预测接下来的十个样本的辛烷值
% 注意要将指标变为列向量,然后再用sim函数预测
predict_y =zeros(10,1);% 初始化predict_y
for i =1:10
result =sim(net,new_X(i,:)');predict_y(i)= result;
end
disp('预测值为:')disp(predict_y)
结果:
预测值为:
87.155086.886787.913784.886585.334184.072486.503286.138388.862886.9989
4.辛烷值的预测(进阶版,预测辛烷值区间)
因为有人进行了提问:bp神经网络预测的问题,讨论区也有类似的问题,所以对辛烷值的预测进行了深入的讨论
上一个是预测一个辛烷值,这次我们将上一次的辛烷值做一个运算,生成一个辛烷值区间(其实就是想生成个一个区间的两个端点),自定义公式:
[
α
,
β
]
=
[
x
−
∣
x
r
a
n
d
i
(
[
9
,
11
]
)
∣
,
x
+
∣
x
r
a
n
d
i
(
[
11
,
13
]
)
∣
]
\left[ \alpha ,\beta \right] =\left[ x-\left| \dfrac{x}{randi([9,11])}\right| ,x+\left| \dfrac{x}{randi([11,13])}\right| \right]
[α,β]=[x−∣∣randi([9,11])x∣∣,x+∣∣randi([11,13])x∣∣]
我们生成
[
α
,
β
]
\left[ \alpha ,\beta \right]
[α,β]:
%init(1)是初始辛烷值,init(2)是α,init(3)是β
for i =1:50init(i,2)=init(1)-init(1)/randi([9,11]);init(i,3)=init(1)+init(1)/randi([11,13]);
end
数据如下(均保存2位小数):
辛烷值 α β
85.376.7792.4185.2577.5592.4188.4576.7791.8683.477.5592.4187.976.7792.4185.575.8293.0588.976.7793.0588.377.5593.0588.775.8293.0588.4575.8292.4188.7575.8291.8688.2576.7793.0587.377.5591.868876.7793.0588.775.8292.4185.576.7793.0588.6576.7791.8688.7575.8293.0585.475.8293.0588.676.7792.418775.8293.0587.1577.5593.0587.0577.5591.8687.2576.7792.4186.8575.8292.4188.6577.5592.4186.676.7793.058676.7792.4186.177.5592.4186.576.7791.8686.375.8291.8684.477.5591.8684.775.8293.0584.676.7791.8684.575.8291.8688.175.8292.4185.2576.7791.8688.477.5591.8688.277.5592.4188.477.5593.0588.5575.8291.8688.3576.7792.4188.277.5592.4185.376.7791.8688.577.5592.4188.2575.8293.058877.5593.0588.8576.7793.0588.4577.5591.8688.776.7792.41
现在我们开始愉快的预测:
首先导入数据:
new_X:需要预测的输入层数据
X:样品的输入层数据
Y:样品的输出层数据
其实就是把Y多增加1列:
4.1.matlab代码实现
%% 此程序为matlab编程实现的BP神经网络
% 清空环境变量
% clear
close all %关闭所有图形窗口
clc
%%第一步 读取数据
input=X;%载入输入数据
output=Y;%载入输出数据
%% 第二步 设置训练数据和预测数据
% 注意要将指标变为列向量
input_train =input(1:40,:)';
output_train =output(1:40,:)';
input_test =input(41:50,:)';
output_test =output(41:50,:)';%节点个数
inputnum=401;% 输入层节点数量
hiddennum=10;% 隐含层节点数量
outputnum=2;% 输出层节点数量
%% 第三本 训练样本数据归一化
[inputn,inputps]=mapminmax(input_train);%归一化到[-1,1]之间,inputps用来作下一次同样的归一化
[outputn,outputps]=mapminmax(output_train);%% 第四步 构建BP神经网络
net=newff(inputn,outputn,hiddennum,{'tansig','purelin'},'trainlm');% 建立模型,传递函数使用purelin,采用梯度下降法训练
W1= net. iw{1,1};%输入层到中间层的权值
B1= net.b{1};%中间各层神经元阈值
W2= net.lw{2,1};%中间层到输出层的权值
B2= net. b{2};%输出层各神经元阈值
%% 第五步 网络参数配置( 训练次数,学习速率,训练目标最小误差等)
net.trainParam.epochs=1000;% 训练次数,这里设置为1000次
net.trainParam.lr=0.01;% 学习速率,这里设置为0.01
net.trainParam.goal=0.00001;% 训练目标最小误差,这里设置为0.00001%% 第六步 BP神经网络训练
net=train(net,inputn,outputn);%开始训练,其中inputn,outputn分别为输入输出样本
%% 第七步 测试样本归一化
inputn_test=mapminmax('apply',input_test,inputps);% 对样本数据进行归一化
%% 第八步 BP神经网络预测
an=sim(net,inputn_test);%用训练好的模型进行仿真
%% 第九步 预测结果反归一化与误差计算
test_simu=mapminmax('reverse',an,outputps);%把仿真得到的数据还原为原始的数量级
error=test_simu-output_test;%预测值和真实值的误差
%%第十步 真实值与预测值误差比较
figure('units','normalized','position',[0.1190.20.380.5])plot(output_test,'bo-')
hold on
plot(test_simu,'r*-')
hold on
plot(error,'square','MarkerFaceColor','b')legend('期望值','预测值','误差')xlabel('数据组数')ylabel('样本值')title('BP神经网络测试集的预测值与实际值对比图')[c,l]=size(output_test);MAE1=sum(abs(error))/l;MSE1=error*error'/l;RMSE1=MSE1^(1/2);disp(['-----------------------误差计算--------------------------'])disp(['隐含层节点数为',num2str(hiddennum),'时的误差结果如下:'])disp(['平均绝对误差MAE为:',num2str(MAE1)])disp(['α的均方误差MSE为: ',num2str(MSE1(1,:))])disp(['β的均方误差MSE为: ',num2str(MSE1(2,:))])disp(['α的均方根误差RMSE为: ',num2str(RMSE1(1,:))])disp(['β的均方根误差RMSE为: ',num2str(RMSE1(2,:))])
之后开始训练:
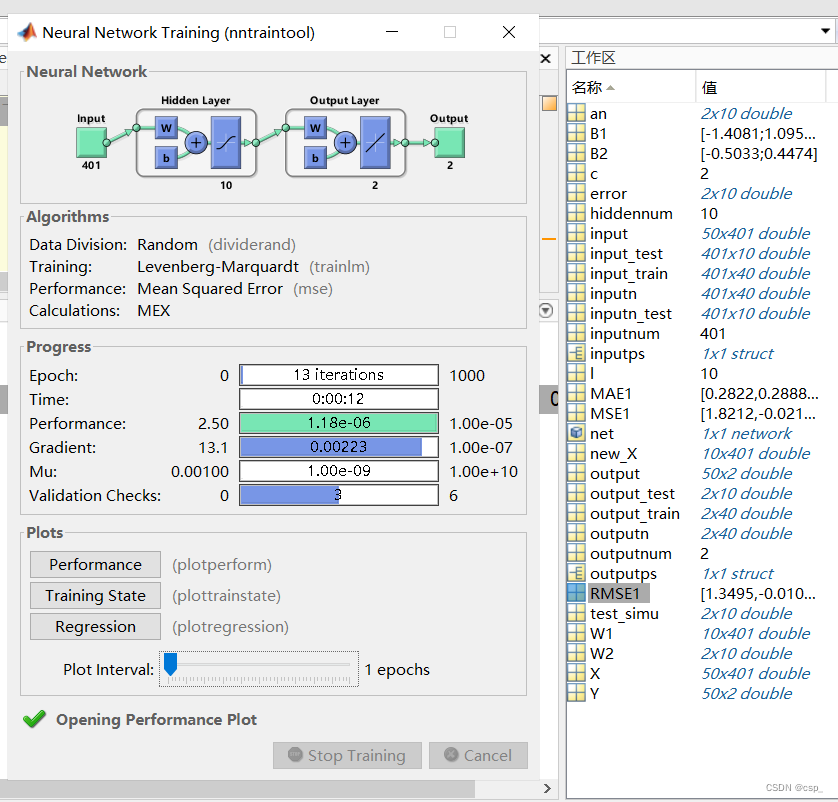
训练结果为:
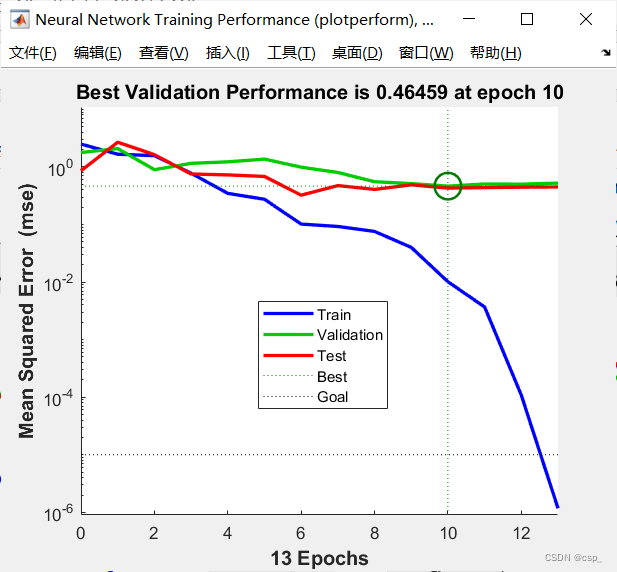
训练中间阶段:
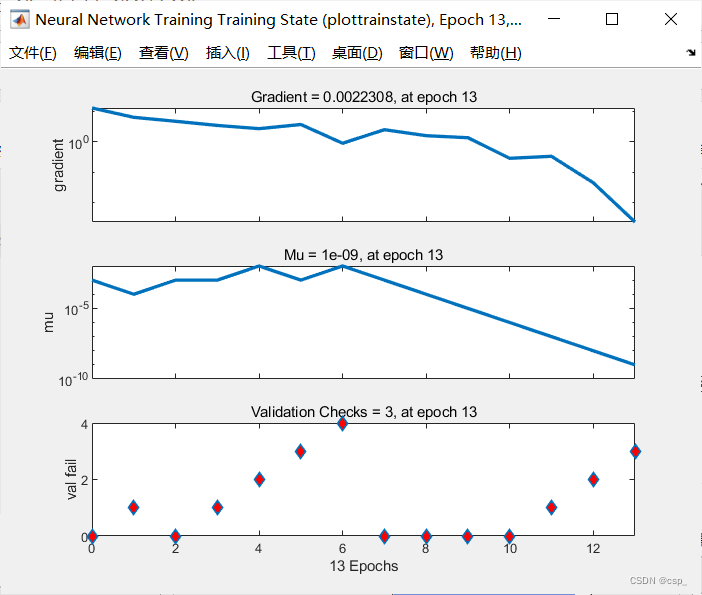
回归结果(数据虽然是瞎生成的,但结果好像还不错呢 ):
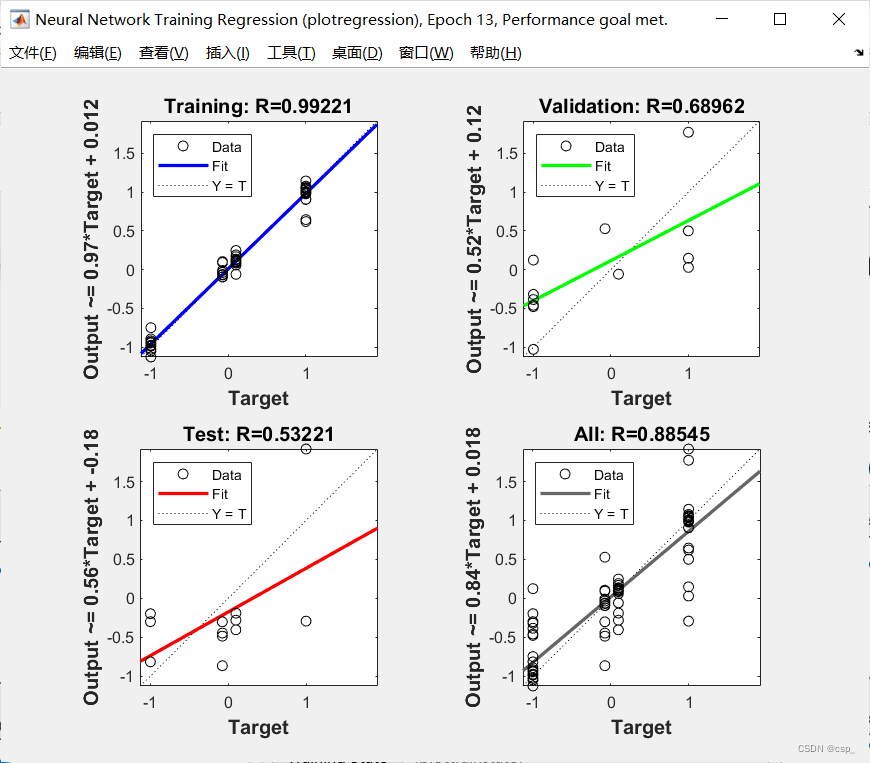
输出结果(图像有些小问题,应该是多条曲线的对比,有空会将它优化的QAQ ,但是整体思路都没问题):
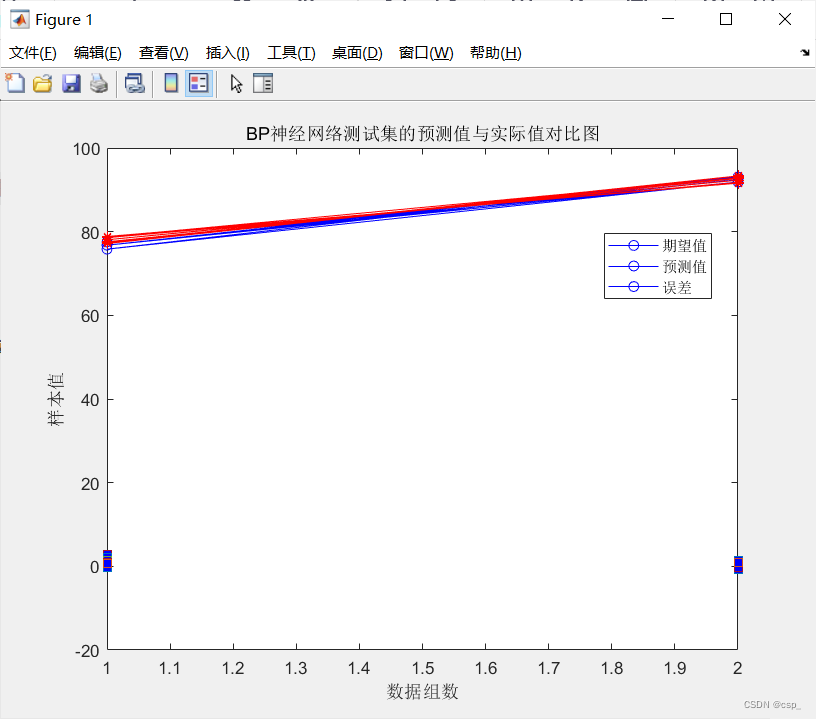
-----------------------误差计算--------------------------
隐含层节点数为10时的误差结果如下:
平均绝对误差MAE为:0.282230.288820.163510.173730.0782390.159540.0457160.110220.160830.16366
α的均方误差MSE为: 1.8212-0.021202
β的均方误差MSE为: -0.0212020.42378
α的均方根误差RMSE为: 1.3495-0.010599
β的均方根误差RMSE为: -0.0105990.6509
进行预测,竟然报错了:
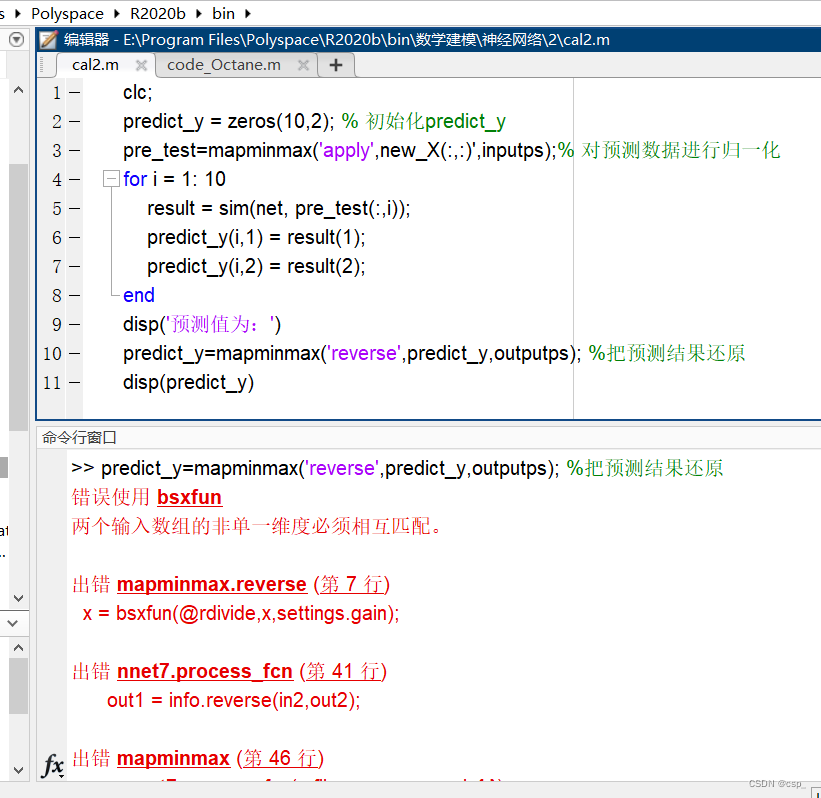
错误代码(就当教训了):
clc;
predict_y =zeros(10,2);% 初始化predict_y
pre_test=mapminmax('apply',new_X(:,:)',inputps);% 对预测数据进行归一化
for i =1:10
result =sim(net,pre_test(:,i));predict_y(i,1)=result(1);predict_y(i,2)=result(2);
end
disp('预测值为:')
predict_y=mapminmax('reverse',predict_y,outputps);%把预测结果还原
disp(predict_y)
我们查看predict_y,没问题:
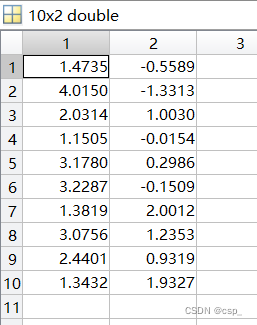
那么就是
mapminmax
函数的问题,修改如下:
clc;
predict_y =zeros(10,2);% 初始化predict_y
pre_test=mapminmax('apply',new_X(:,:)',inputps);% 对预测数据进行归一化
for i =1:10
result =sim(net,pre_test(:,i));predict_y(i,1)=result(1);predict_y(i,2)=result(2);
end
disp('预测值为:')
predict_y=predict_y';
predict_y=mapminmax('reverse',predict_y,outputps);%把预测结果还原
disp(predict_y)
结果:
预测值为:
77.959680.158078.442177.680279.433979.477977.880379.345478.795777.846992.122591.662993.051892.445992.632692.365293.645793.190093.009593.6050
看一下predict_y,也没问题:

我们再转置回来得到正确结果:
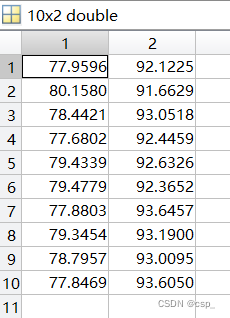
那么为啥要这么修改呢,我们细细品(#^.^#) ,这要回到神经网络构建的时候了:
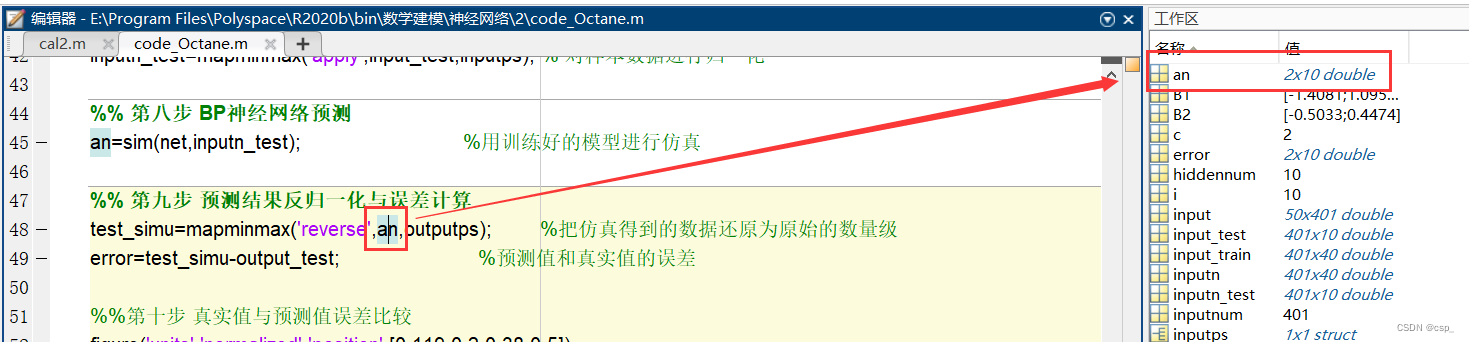
这两部分要对应上哇,哈哈,完结撒花
4.2.工具箱实现
类比之前实现的方法,其实是不难实现的,读者可以自行完成
目前课业压力较大,这段时间大概率会忽略博客评论,敬请谅解
版权归原作者 csp_ 所有, 如有侵权,请联系我们删除。