为什么要以均方误差作为损失函数?(将模型在每个训练样本上的预测误差加和,来衡量整体样本的准确性)
解:利用均方误差画出来的图像有如下特点
- 曲线的最低点是可导的。
- 越接近最低点,曲线的坡度逐渐放缓,有助于通过当前的梯度来判断接近最低点的程度(是否逐渐减少步长,以免错过最低点)
标准神经网络的构成:
神经网络的标准结构中每个神经元由加权和与非线性变换构成,然后将多个神经元分层的摆放并连接形成神经网络。
深度学习的基本步骤:
1.数据处理 ( 数据预处理 )
2.模型设计 ( 网络结构的设计 )
3.训练配置 ( 优化器,计算资源 )
4.正式训练 ( 前向计算,损失函数,后向传播 )
5.模型保存 ( 保存训练好的模型,以备预测调用 )
深度学习模型的三要素:
模型结构三要素(模型假设、评价函数和优化算法)
在学习深度学习的时候,可以遵循深度学习的基本步骤,对于深度学习模型来讲,处理模型的三要素不同之外,其余均相同,步骤一致。
数据处理:
数据处理包含五个部分:数据导入、数据形状变换、数据集划分、数据归一化处理和封装
load data
函数。数据预处理后,才能被模型调用。
划分数据集:
数据集划分成训练集和测试集,其中训练集用于确定模型的参数,测试集用于评判模型的效果。
数据归一化处理:
对每个特征进行归一化处理,使得每个特征的取值缩放到0~1之间。这样做有两个好处:一是模型训练更高效,二是特征前的权重大小可以代表该变量对预测结果的贡献度(因为每个特征值本身的范围相同)。特征输入归一化后,不同参数输出的Loss是一个比较规整的曲线,学习率可以设置成统一的值 ;特征输入未归一化时,不同特征对应的参数所需的步长不一致,尺度较大的参数需要大步长,尺寸较小的参数需要小步长,导致无法设置统一的学习率。
通过遍历feature_num里的每一个数据,将Max和Min的记录下来,并通过Max-Min作为基数(即Min=0,Max=1)进行数据的归一化处理:其中Max为样本数据的最大值,Min为样本数据的最小值。可参考下示公式:
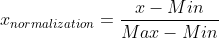
for i in range(feature_num):
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
数据处理操作封装成
load data
函数,以便下一步模型的调用
模型设计是深度学习模型关键要素之一,也称为网络结构设计,相当于模型的假设空间,即实现模型“前向计算”(从输入到输出)的过程。
随机数种子的作用是:保持程序每次运行结果的一致性。
模型设计完成后,需要通过训练配置寻找模型的最优值,即通过损失函数来衡量模型的好坏。
回归问题中,均方误差是一种比较常见的形式,分类问题中通常会采用交叉熵作为损失函数
计算损失函数时需要把每个样本的损失函数值都考虑到,所以我们需要对单个样本的损失函数进行求和,并除以样本总数N ( 均方误差的公式 )
模型训练过程是深度学习模型的关键要素之一,其目标是让定义的损失函数LossLossLoss尽可能的小。
梯度下降法:
在现实中存在大量的函数正向求解容易,但反向求解较难,被称为单向函数,这种函数在密码学中有大量的应用。密码锁的特点是可以迅速判断一个密钥是否是正确的(已知xxx,求yyy很容易),但是即使获取到密码锁系统,也无法破解出正确得密钥(已知yyy,求xxx很难)。
这种情况特别类似于一位想从山峰走到坡谷的盲人,他看不见坡谷在哪(无法逆向求解出Loss导数为0时的参数值),但可以伸脚探索身边的坡度(当前点的导数值,也称为梯度)。那么,求解Loss函数最小值可以这样实现:从当前的参数取值,一步步的按照下坡的方向下降,直到走到最低点。计算直到损失函数不在下降为止!!
第一要保证L是下降的,第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们:沿着梯度的反方向,是函数值下降最快的方向,简单理解,函数在某一个点的梯度方向是曲线斜率最大的方向,但梯度方向是向上的,所以下降最快的是梯度的反方向。
下示为machine learning中线性回归解的梯度下降求解:

更新梯度:
net.w[5] = net.w[5] - eta * gradient_w5
- 相减:参数需要向梯度的反方向移动。
- eta:控制每次参数值沿着梯度反方向变动的大小,即每次移动的步长,又称为学习率。
随机梯度下降法( Stochastic Gradient Descent,SGD):
梯度下降每次损失函数和梯度计算都是基于数据集中的全量数据,对于小型数据集来讲,是适合的,但是后面遇到大型数据集就不适用了,如果每次都使用全量数据进行计算,效率非常低。
由于参数每次只沿着梯度反方向更新一点点,因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体,基于这部分数据计算梯度和损失来更新参数,这种方法被称作随机梯度下降法(Stochastic Gradient Descent,SGD)。
SGD的核心要素:
- mini-batch:每次迭代时抽取出来的一批数据被称为一个mini-batch。
- batch_size:一个mini-batch所包含的样本数目称为batch_size。
- epoch:当程序迭代的时候,按mini-batch逐渐抽取出样本,当把整个数据集都遍历到了的时候,则完成了一轮训练,也叫一个epoch。启动训练时,可以将训练的轮数num_epochs和batch_size作为参数传入。
为了实现随机抽样的效果,我们先将train_data里面的样本顺序随机打乱,然后再抽取mini_batch。随机打乱样本顺序,需要用到
np.random.shuffle(A)
函数.,A为需要乱序的向量,矩阵等
大量实验发现,模型受训练后期的影响更大,类似于人脑总是对近期发生的事情记忆的更加清晰。为了避免数据样本集合的顺序干扰模型的训练效果,需要进行样本乱序操作。当然,如果训练样本的顺序就是样本产生的顺序,而我们期望模型更重视近期产生的样本(预测样本会和近期的训练样本分布更接近),则不需要乱序这个步骤。
使用随机梯度下降(SGD)时,训练代码修改如下:
将每个随机抽取的mini-batch数据输入到模型中用于参数训练。训练过程的核心是两层循环:
- 第一层循环,代表样本集合要被训练遍历几次,称为“epoch”,代码如下:
for epoch_id in range(num_epochs):
- 第二层循环,代表每次遍历时,样本集合被拆分成的多个批次,需要全部执行训练,称为“iter (iteration)”,代码如下:
for iter_id,mini_batch in emumerate(mini_batches):
在两层循环的内部是经典的四步训练流程:前向计算->计算损失->计算梯度->更新参数,

梯度下降与随机梯度下降对比:

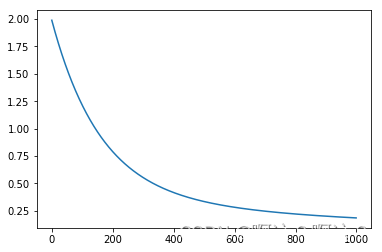
上述Loss的变化,随机梯度下降加快了训练过程,但由于每次仅基于少量样本更新参数和计算损失,所以损失下降曲线会出现震荡
链式法则:
链式法则是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。复合函数的导数将是构成复合这有限个函数在相应点的导数的乘积,就像锁链一样一环套一环,故称链式法则。如下图所示,如果求最终输出对内层输入(第一层)的梯度,等于外层梯度(第二层)乘以本层函数的梯度。

版权归原作者 啊这?啊这? 所有, 如有侵权,请联系我们删除。