注：本套试卷为人工智能专业期末考试试卷，该门课对于人工智能专业同学为考试课，对其他专业同学为专业限选课程（考查课），所以该题仅作为人工智能专业同学复习参考。
百度网盘资源下载（含word原版与pdf版）：https://pan.baidu.com/s/1OEAxweaYijzsgypU2282fg
提取码：hit6
一.填空题（每空1分，共22分）
1.通过对矩阵进行高斯消元来对矩阵进行A=LU分解，假设原矩阵为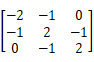
，则L=____________，U=____________。
2.假设函数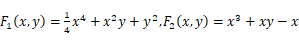
，分别计算其二阶Hessian矩阵
____________，
____________。
3.m×n的矩阵，假设其行空间维数为r，零空间维数为s，则r+s=____________。
4.矩阵特征值中，当几何重数GM____代数重数AM时，矩阵不能对角化。
5.逆时针旋转角度θ的2×2单位旋转矩阵为：____________。
6.δ(t)与____________构成一对傅里叶变换对。
7.对于强噪信道的输入输出分别为X，Y，则I(X;Y)=____________，对于一般的信道，则I(X;Y)=____________。（用X,Y的熵和联合熵的表达式表示）
8.回归问题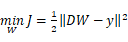
的解析解W=____________，其梯度下降法的迭代公式为：____________。
9.对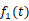
和
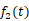分别进行傅里叶变换可得
和
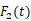，则对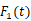
*
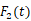进行傅里叶逆变换可得：____________。
10.设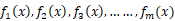
均为凸函数，请问凸函数的交集________（是/不是）凸函数。
11.最优化问题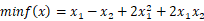
，取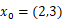
，则该点处的梯度方向为____________，最快下降方向为____________。
12.线性规划问题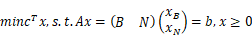
，设基本解为
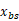，则其基本形式为____________（或者用文字描述要满足的条件也可以）。
13.最优化方法中，最小化可微目标函数f(x)，在点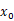
处的梯度表示为
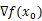，该点处的方向向量表示为
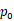，则方向
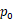称为点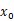
处的下降方向，如果梯度向量
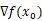与方向向量满足如下关系：____________。
14.优化问题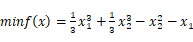
的严格局部极小值为____________。
15.函数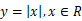
在x=0点的次微分为____________。
16.
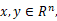则点y到集合
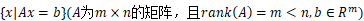的投影为____________。
二.判断题（每个括号1分，共14分）
17.矩阵的行空间与零空间正交，矩阵的列空间与其转置矩阵的零空间正交（ ）
18.矩阵A的特征值是2,2,5，则矩阵必定可逆（ ）
19.矩阵A的唯一特征向量是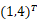
的倍数，则必定不可逆（ ）；有重复的特征值（ ）；不能对角化为
（ ）
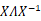20.离散信源熵的最大值是当信源符号相互独立，概率分布均匀的时候获得（ ）
21.如果某个系统算子为g(n)=af(n)+b，则该系统是线性系统（ ）
22.图像的2维傅里叶变换后，可得幅度谱和相位谱，其中相位谱更重要（ ）
23.求解方程中，系数矩阵的条件数越大越好（ ）
24.Sherman-Morrison公式的主要作用是将n×n矩阵求逆问题转化为一个低阶k×k矩阵的求逆问题，从而降低求逆的复杂度（ ）
25.相对熵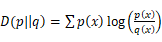
非负（ ）
26.线性规划问题的最优解必定是其基本可行解（ ）
27.可以采用混合同余法生成均匀分布的随机数（ ）
28.常用的随机变量模拟方法有逆变换法、拒绝抽样法等方法（ ）
二.简答题（每题4分，共28分）
（试卷上题号打错了，此处及以后特意保留）
29.简述奈奎斯特(Nyquist)采样定理的基本内容并解释混叠产生的原因。
30.高斯消元法和LU分解的复杂性一样，为何还需要做LU分解，请举例说明。
31.请结合课程内容解释逼近思想。
32.请介绍PCA基本原理。
33.请形式化描述K-means算法用于矢量量化的稀疏表示问题。
34.请描述贝叶斯准则、最大后验概率准则、最大似然准则的基本假设及其表达方式。
35.请介绍有约束优化问题及其对偶问题的形式化表达方式，并介绍弱对偶与强对偶定理的基本内容。
三.计算和证明题（第36题8分，第37题10分，第38题8分，共26分）
36.请判断函数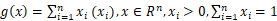
的凹凸性，并给出证明。
37.给定线性规划问题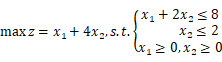
，请：
a).将其转化为标准形式。
b).给出基本可行解，并计算其最优值。
38.给出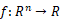函数
的共轭函数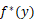
的定义，并计算
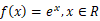的共轭函数。
四.论述题（每题5分，共10分）
39.通过对实际问题进行形式化建模，表达为优化问题，然后获取数据并进行标注，进一步根据数据采用有监督机器学习算法来拟合数据的分布，请根据本课程内容，谈谈你对人工智能应用的基本理解（如基本流程、存在的问题与挑战、以后的发展趋势等都可以）。
40.请谈谈对课程内容的建议。
版权归原作者 CulfateBurner 所有， 如有侵权，请联系我们删除。