图解AI数学基础 | 概率与统计

1.概率论及在AI中的使用

概率（Probability），反映随机事件出现的可能性大小。事件AAA出现的概率，用P(A)P(A)P(A)表示。

概率论（Probability Theory），是研究随机现象数量规律的数学分支，度量事物的不确定性。

机器学习大部分时候处理的都是不确定量或随机量。因此，相对计算机科学的其他许多分支而言，机器学习会更多地使用概率论。很多典型的机器学习算法模型也是基于概率的，比如朴素贝叶斯（Naive Bayesian）等。

在人工智能领域，概率论有广泛的应用：

• 可以借助于概率方法设计算法（概率型模型，如朴素贝叶斯算法）。
• 可以基于概率与统计进行预测分析（如神经网络中的softmax）。

2.随机变量（Random Variable）

简单地说，随机变量是指随机事件的数量表现，是可以『随机』地取不同值的『变量』。通常，用大写字母来表示随机变量本身，而用带数字下标的小写字母来表示随机变量能够取到的值。

• 例如，XXX为随机变量，x1x_{1}x1、x2x_{2}x2、xix_{i}xi是随机变量XXX可能的取值。

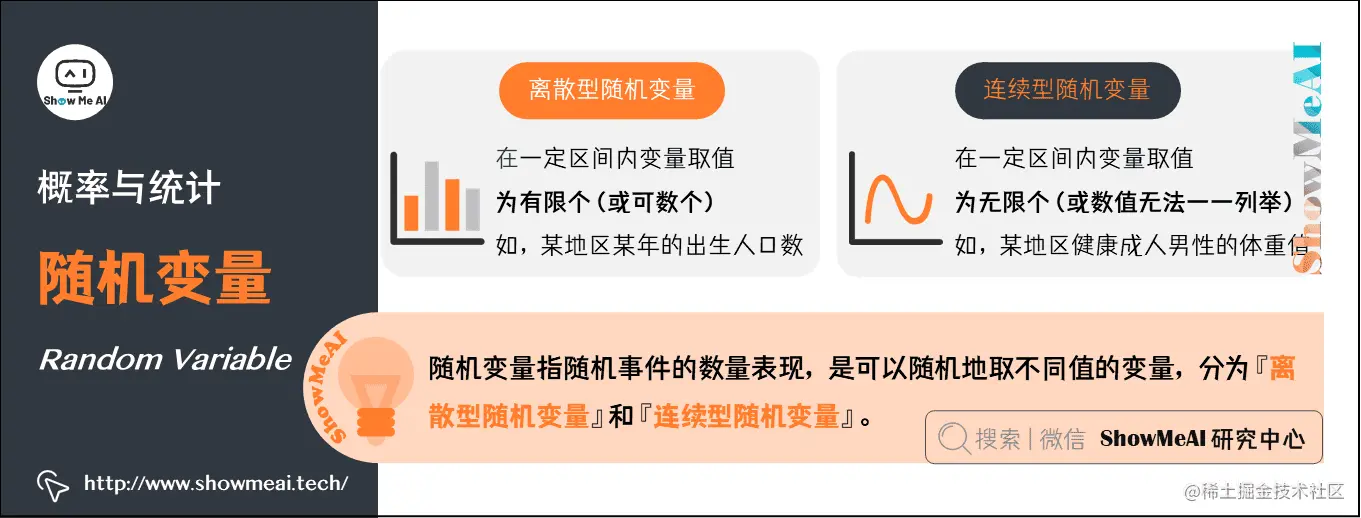
随机变量可以分为『离散型随机变量』和『连续型随机变量』：

• 离散型随机变量（discrete random variable）：即在一定区间内变量取值为有限个（或可数个）。例如，某地区某年的出生人口数。
• 连续型随机变量（continuous random variable）：即在一定区间内变量取值为无限个（或数值无法一一列举出来）。例如，某地区男性健康成人的体重值。

3.随机向量（Random Vector）

将几个随机变量按顺序放在一起，组成向量的形式，就是随机向量。

在样本空间全部都一样的情况下，一个nnn维的随机向量是x(ξ)→=(x1(ξ)x2(ξ)⋯xn(ξ))x \overrightarrow{(\xi)}=\left(\begin{array}{c} x_{1}(\xi) \ x_{2}(\xi) \ \cdots \ x_{n}(\xi) \end{array}\right)x(ξ)=⎝⎛x1(ξ)x2(ξ)⋯xn(ξ)⎠⎞

其中，ξ\xiξ就是样本空间中的样本点。随机变量是１维随机向量的特殊情况。

4.概率分布（Probability Distribution）

广义上，概率分布用于表述随机变量取值的概率规律。或者说，给定某随机变量的取值范围，概率分布表示该随机事件出现的可能性。

狭义地，概率分布指随机变量地概率分布函数，也称累积分布函数（Cumulative Distribution Function，CDF）。

离散型随机变量的概率分布：

• 使用分布列描述离散型随机变量的概率分布，即给出离散型随机变量的全部取值及每个值的概率。
• 常见的离散型随机变量的分布有：单点分布、0-1分布、几何分布、二项分布、泊松分布等。

连续型随机变量的概率分布：

如果随机变量XXX的分布函数为F(x)F(x)F(x)，存在非负函数f(x)f (x)f(x)使对于任意实数xxx有F(x)=∫−∞xf(t)dtF(x)=\int_{-\infty}^{x} f(t) d tF(x)=∫−∞xf(t)dt，则称XXX为连续型随机变量 ，其中函数f(x)f(x)f(x)称为XXX的概率密度函数。

常见的连续型随机变量的分布有：正态分布、均匀分布、指数分布、t−t-t−分布、F−F-F−分布、ξ2−\xi^{2}-ξ2−分布等。

机器学习中一个典型的概率分布应用，是分类问题中，很多模型最终会预估得到样本属于每个类别的概率，构成1个概率向量，表征类别概率分布。

5.条件概率（Conditional Probability）

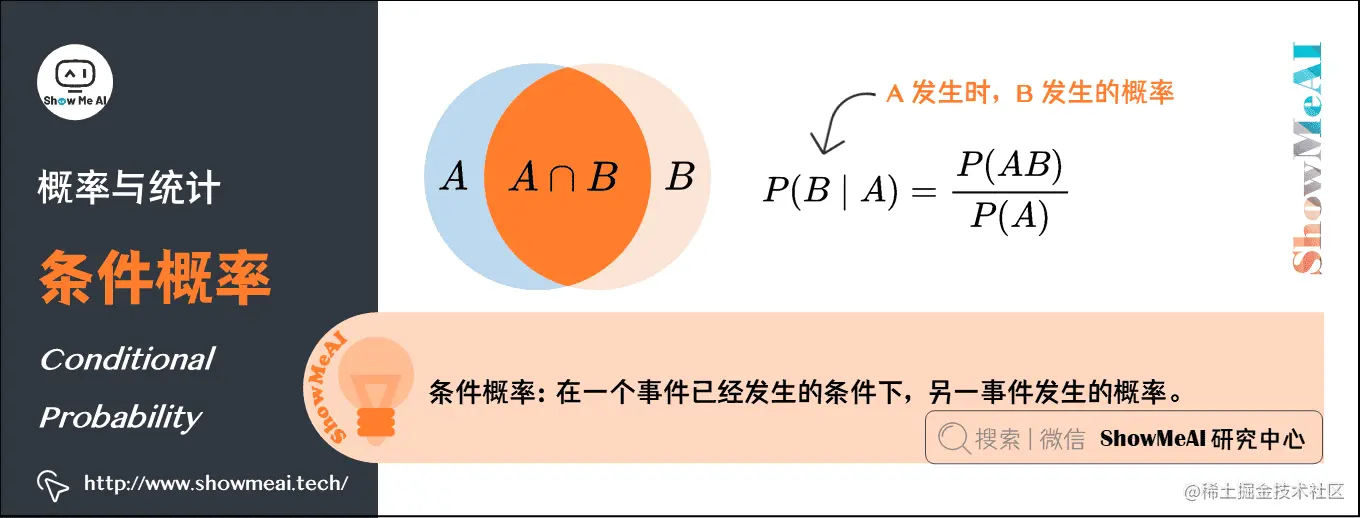
很多情况下我们感兴趣的是，某个事件在给定其它事件发生时出现的概率，这种概率叫条件概率。

给定AAA时BBB发生的概率记为P(B∣A)P(B \mid A)P(B∣A)，概率的计算公式为：P(B∣A)=P(AB)P(A)P(B \mid A)=\frac{P(A B)}{P(A)}P(B∣A)=P(A)P(AB)

6.贝叶斯公式（Bayes’ Theorem）

先看看什么是“先验概率”和“后验概率”，以一个例子来说明：

先验概率：某疾病在人群中发病率为0.1%，那某人没有做检验之前，预计患病率为P( 患病 )=0.1%P(\text { 患病 })=0.1 %P( 患病 )=0.1%，这个概率就叫做『先验概率』。

后验概率：该疾病的检测准确率为95%，即该病患者检测显示阳性的概率为95%（检测显示阴性的概率为5%），即P( 显示阳性|患病 )=95%P(\text { 显示阳性|患病 })=95%P( 显示阳性|患病 )=95%；或者说未患病的检测者，检测结果显示阴性的概率为95%，检测显示阳性的概率为5%。那么，检测显示为阳性时，此人的患病概率P( 患病| 显示阳性)P(\text { 患病| 显示阳性})P( 患病| 显示阳性)就叫做『后验概率』。

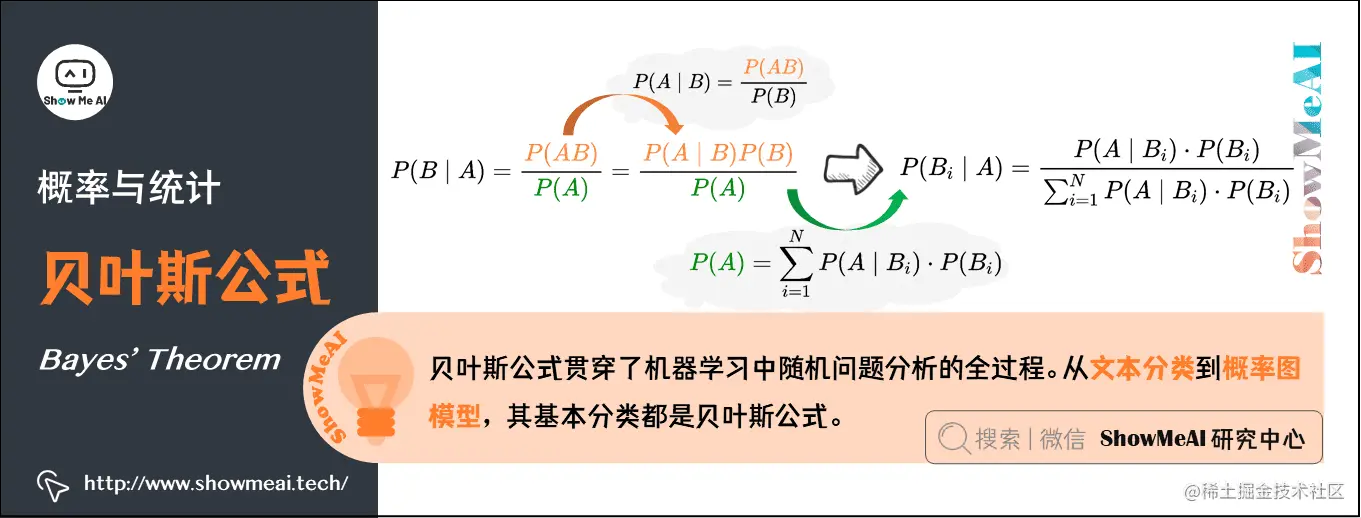
贝叶斯公式：贝叶斯提供了一种利用『先验概率』计算『后验概率』的方法：

• 条件概率公式：P(B∣A)=P(AB)P(A)P(B \mid A)=\frac{P(A B)}{P(A)}P(B∣A)=P(A)P(AB)，P(A∣B)=P(AB)P(B)P(A \mid B)=\frac{P(A B)}{P(B)}P(A∣B)=P(B)P(AB)
• 由条件概率公式变换得到乘法公式：P(AB)=P(B∣A)P(A)=P(A∣B)P(B)P(A B)=P(B \mid A) P(A)=P(A \mid B) P(B)P(AB)=P(B∣A)P(A)=P(A∣B)P(B)
• 将条件概率公式和乘法公式结合：P(B∣A)=P(A∣B)⋅P(B)P(A)P(B \mid A)=\frac{P(A \mid B) \cdot P(B)}{P(A)}P(B∣A)=P(A)P(A∣B)⋅P(B)
• 引入全概率公式：P(A)=∑i=1NP(A∣Bi)⋅P(Bi)P(A)=\sum_{i=1}^{N} P\left(A \mid B_{i}\right) \cdot P\left(B_{i}\right)P(A)=∑i=1NP(A∣Bi)⋅P(Bi)
• 将全概率代入P(B∣A)P(B \mid A)P(B∣A)，可以得到贝叶斯公式：P(Bi∣A)=P(A∣Bi)⋅P(Bi)∑i=1NP(A∣Bi)⋅P(Bi)P\left(B_{i} \mid A\right)=\frac{P\left(A \mid B_{i}\right) \cdot P\left(B_{i}\right)}{\sum_{i=1}^{N} P\left(A \mid B_{i}\right) \cdot P\left(B_{i}\right)}P(Bi∣A)=∑i=1NP(A∣Bi)⋅P(Bi)P(A∣Bi)⋅P(Bi)

上述例子的计算结果： P( 患病 ∣ 显示阳性 )=P( 显示阳性|患病 )P( 患病 )P( 显示阳性 )=P( 显示阳性|患病 )P( 患病 )P( 显示阳性|患病 )P( 患病 )+P( 显示阳性|无病) P( 无病 )=95%∗0.1%95%∗0.1%+5%∗99.9%=1.86%\begin{aligned} P(\text { 患病 } \mid \text { 显示阳性 }) &=\frac{P(\text { 显示阳性|患病 }) P(\text { 患病 })}{P(\text { 显示阳性 })} \ &=\frac{P(\text { 显示阳性|患病 }) P(\text { 患病 })}{P(\text { 显示阳性|患病 }) P(\text { 患病 })+P(\text { 显示阳性|无病) } P(\text { 无病 })} \ &=\frac{95 % * 0.1 %}{95 % * 0.1 %+5 % * 99.9 %}=1.86 % \end{aligned}P( 患病 ∣ 显示阳性 )=P( 显示阳性 )P( 显示阳性|患病 )P( 患病 )=P( 显示阳性|患病 )P( 患病 )+P( 显示阳性|无病) P( 无病 )P( 显示阳性|患病 )P( 患病 )=95%∗0.1%+5%∗99.9%95%∗0.1%=1.86%

贝叶斯公式贯穿了机器学习中随机问题分析的全过程。从文本分类到概率图模型，其基本分类都是贝叶斯公式。

期望、方差、协方差等主要反映数据的统计特征。机器学习的一个很大应用就是数据挖掘等，因此这些基本的统计概念也是很有必要掌握。另外，像后面的EM算法中，就需要用到期望的相关概念和性质。

7.期望（Expectation）

在概率论和统计学中，数学期望是试验中每次可能结果的概率乘以其结果的总和。期望是最基本的数学特征之一，反映随机变量平均值的大小。

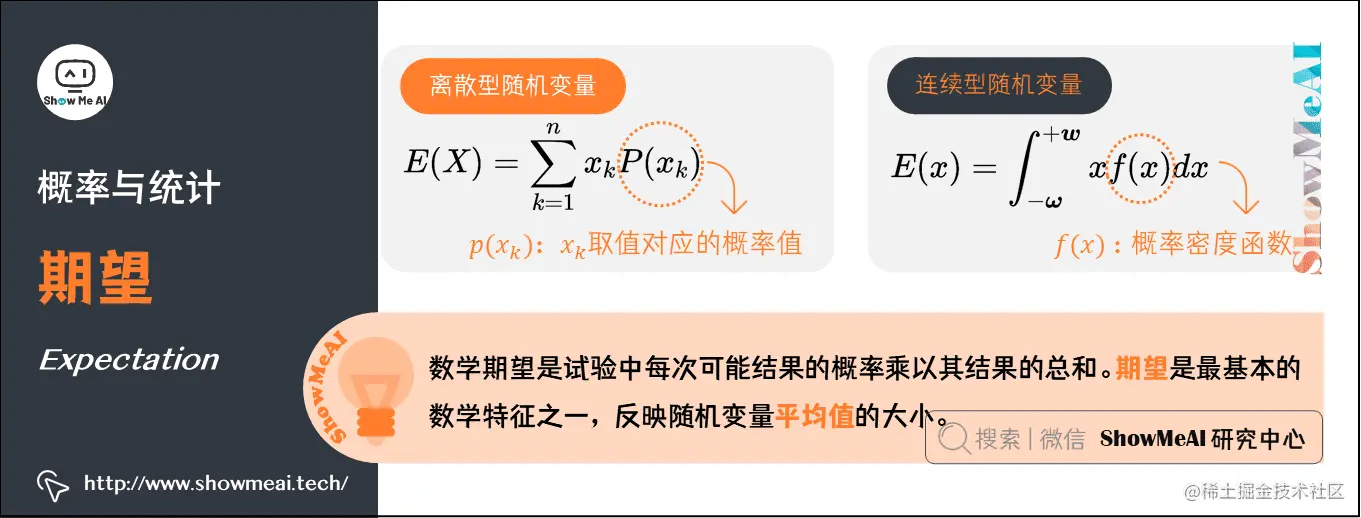
假设XXX是一个离散型随机变量，其可能的取值有{x1,x2,…,xn}\left{x_{1}, x_{2}, \ldots, x_{n}\right}{x1,x2,…,xn}，各取值对应的概率取值为P(xk)P\left(x_{k}\right)P(xk)，k=1,2,…,nk=1, 2, \ldots, nk=1,2,…,n。其数学期望被定义为：

E(X)=∑k=1nxkP(xk)E(X)=\sum_{k=1}^{n} x_{k} P\left(x_{k}\right)E(X)=∑k=1nxkP(xk)

假设xxx是一个连续型随机变量，其概率密度函数为f(x)f(x)f(x)，其数学期望被定义为：

E(x)=∫−ω+wxf(x)dxE(x)=\int_{-\boldsymbol{\omega}}^{+\boldsymbol{w}} x f(x) d xE(x)=∫−ω+wxf(x)dx

8.方差（Variance）

在概率论和统计学中，样本方差，是各个样本数据分别与其平均数之差的平方和的平均数。方差用来衡量随机变量与其数学期望之间的偏离程度。

离散型：（μ\muμ表示期望）

D(X)=∑k=1n(xk−μ)2D(X)=\sum_{k=1}^{n} \left(x_{k}-\mu\right)^{2}D(X)=∑k=1n(xk−μ)2

一个快速计算方差的公式（即平方的期望减去期望的平方）：

D(X)=E{[X−E(X)]2}=E(X2)−[E(X)]2D(X)=E\left{[X-E(X)]{2}\right}=E\left(X{2}\right)-[E(X)]^{2}D(X)=E{[X−E(X)]2}=E(X2)−[E(X)]2

连续型：（μ\muμ表示期望）

D(x)=∫(x−μ)2f(x)dxD(x)=\int(x-\mu)^{2} f(x) d xD(x)=∫(x−μ)2f(x)dx

9.协方差（Covariance）

在概率论和统计学中，协方差被用于衡量两个随机变量XXX和YYY之间的总体误差。期望值分别为E[X]E[X]E[X]与E[Y]E[Y]E[Y]的两个实随机变量XXX与YYY之间的协方差为：

Cov(X,Y)=E[X−E(X)][Y−E(Y)]=E(XY)−E(X)E(Y)Cov(X,Y) =E { [X-E(X)][Y-E(Y)] } =E(XY)-E(X)E(Y)Cov(X,Y)=E[X−E(X)][Y−E(Y)]=E(XY)−E(X)E(Y)

以下是几个常用等式： Cov(X,Y)=Cov(Y,X)Cov(X, Y)=Cov(Y, X)Cov(X,Y)=Cov(Y,X) Cov(X,X)=D(X)Cov(X, X)=D(X)Cov(X,X)=D(X) D(X+Y)=D(X)+D(Y)+2Cov(X,Y)D(X+Y)=D(X)+D(Y)+2 Cov(X, Y)D(X+Y)=D(X)+D(Y)+2Cov(X,Y) Cov(X,Y)=E(XY)−E(X)E(Y)Cov(X, Y)=E(X Y)-E(X) E(Y)Cov(X,Y)=E(XY)−E(X)E(Y)

10.相关系数（Correlation coefficient）

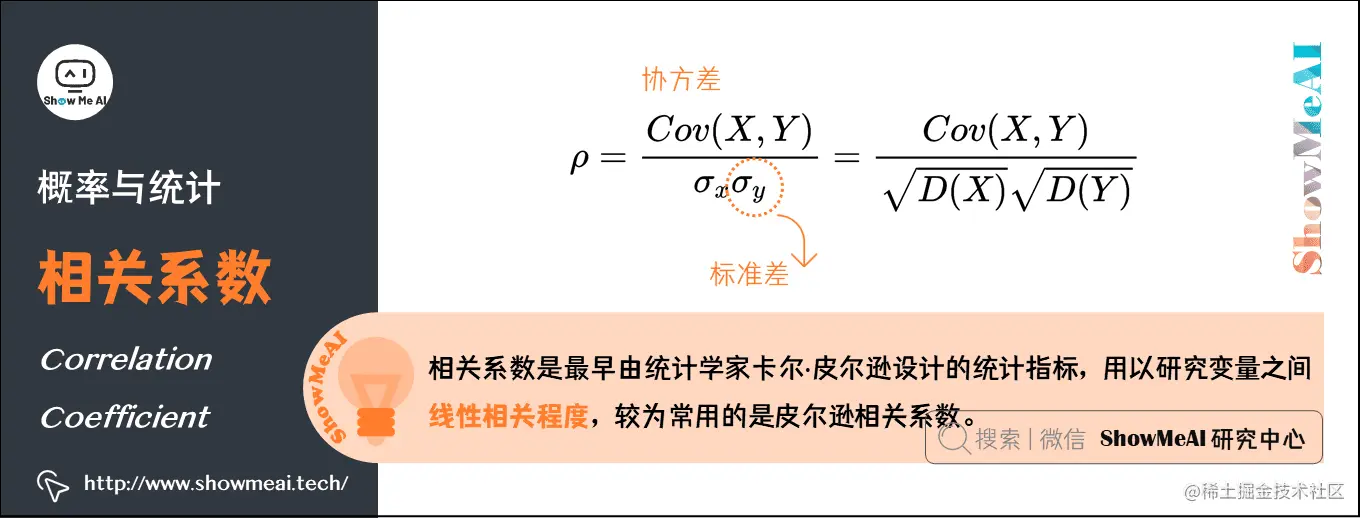
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标，用以研究变量之间线性相关程度。相关系数有多种定义方式，较为常用的是皮尔逊相关系数。从协方差中会得到引申，就是关联系数，即：（σ\sigmaσ是标准差）

ρ=Cov(X,Y)σxσy\rho = \frac{Cov(X,Y)}{\sigma _{x} \sigma _{y}}ρ=σxσyCov(X,Y)

这个公式还有另外的一个表达形式：

ρ=Cov(X,Y)D(X)D(Y)\rho = \frac{Cov(X,Y)}{\sqrt{D(X)} \sqrt{D(Y)}}ρ=D(X)D(Y)Cov(X,Y)

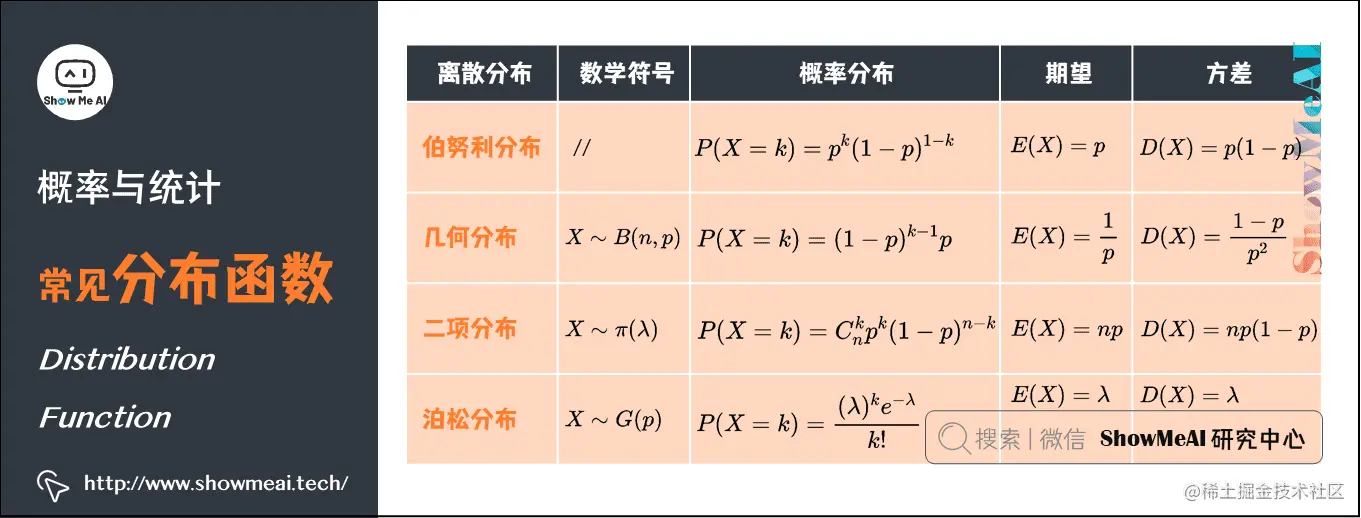
11.常见分布函数

1）伯努利分布（Bernoulli Distribution）（离散型）

在概率论和统计学中，伯努利分布也叫0-1分布，是单个二值型离散随机变量的分布。

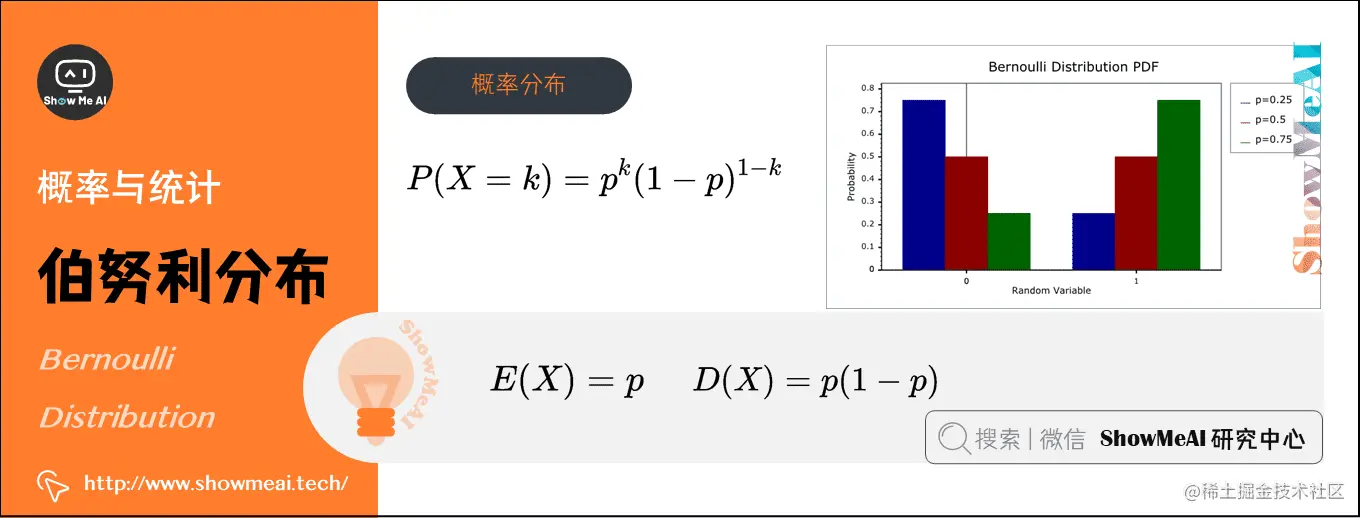
• 概率分布函数：P(X=k)=pk(1−p)1−kP(X=k)=p{k}(1-p){1-k}P(X=k)=pk(1−p)1−k
• 期望：E(X)=pE(X)=pE(X)=p
• 方差：D(X)=p(1−p)D(X)=p(1-p)D(X)=p(1−p)

2）几何分布（Geometric Distribution）（离散型）

在概率论和统计学中，几何分布是离散型概率分布，数学符号为X∼G§X\sim G§X∼G§。其定义为：在nnn次伯努利试验中，试验kkk次才得到第一次成功的机率（即前k−1k-1k−1次皆失败，第kkk次成功的概率）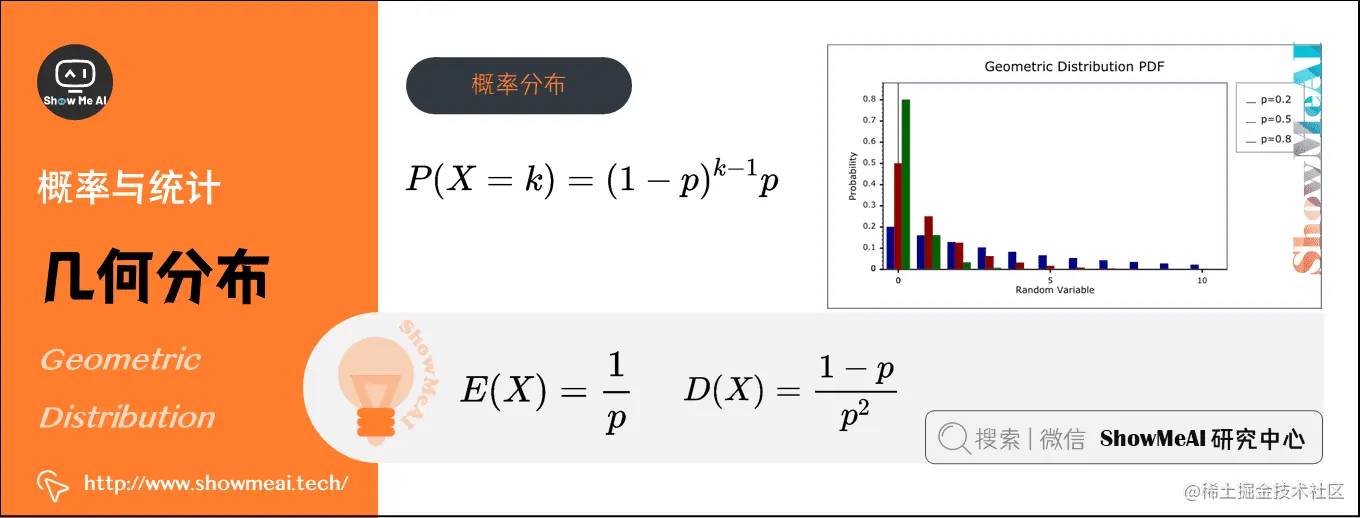

• 概率分布函数：P(X=k)=(1−p)k−1pP(X=k)=(1-p)^{k-1} pP(X=k)=(1−p)k−1p
• 期望：E(X)=1pE(X)=\frac{1}{p}E(X)=p1
• 方差：D(X)=1−pp2D(X)=\frac{1-p}{p^{2}}D(X)=p21−p

3）二项分布（Binomial Distribution）（离散型）

在概率论和统计学中，二项分布即重复nnn次伯努利试验，各次试验之间都相互独立，并且每次试验中只有两种可能的结果，而且这两种结果发生与否相互对立，数学符号为X∼B(n,p)X∼B(n,p)X∼B(n,p)。

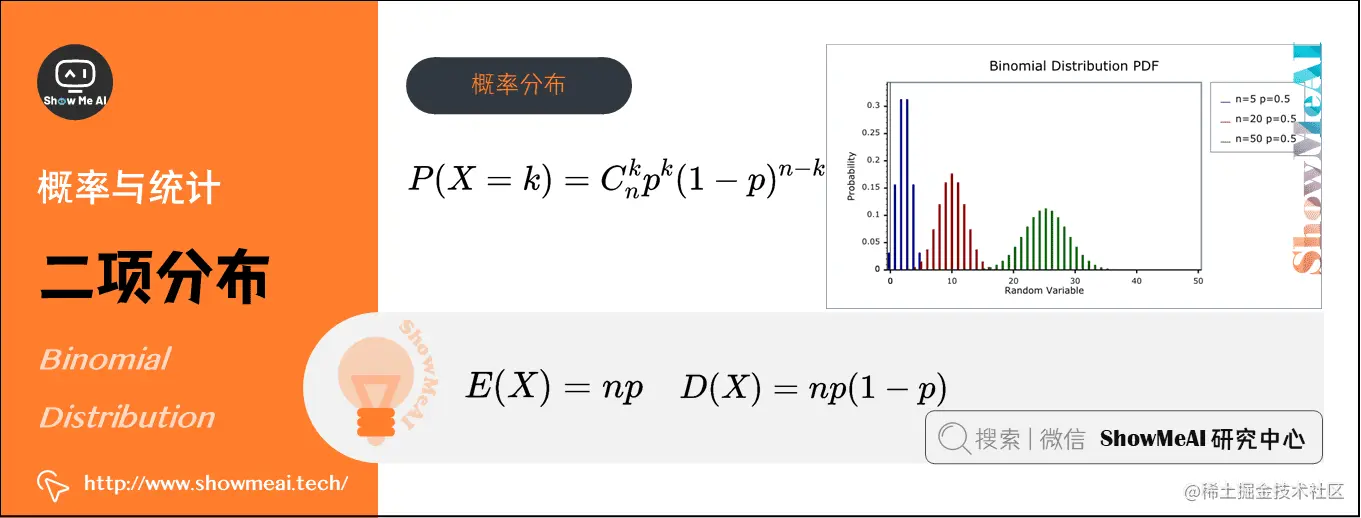如果每次试验时，事件发生的概率为ppp，不发生的概率为1−p1-p1−p，则nnn次重复独立试验中发生kkk次的概率为：P(X=k)=Cnkpk(1−p)n−kP(X=k)=C_{n}^{k} p{k}(1-p){n-k}P(X=k)=Cnkpk(1−p)n−k

• 期望：E(X)=npE(X)=n pE(X)=np
• 方差：D(X)=np(1−p)D(X)=n p(1-p)D(X)=np(1−p)

4）泊松分布（Poisson Distribution）（离散型）

在概率论和统计学中，泊松分布是一种统计与概率学里常见到的离散概率分布，用于描述某段时间内事件具体的发生概率，数学符号为X∼π(λ)X∼\pi \left ( \lambda \right )X∼π(λ)。

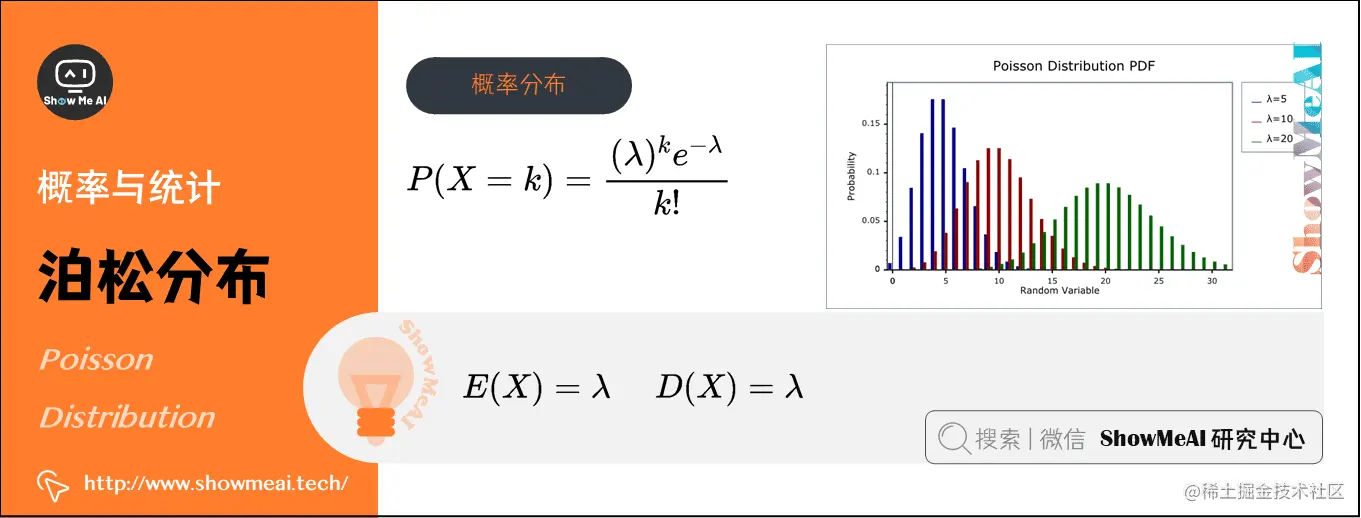泊松分布的参数λ\lambdaλ表示单位时间(或单位面积)内随机事件的平均发生次数，其概率分布函数为：P(X=k)=(λ)ke−λk!P(X=k)=\frac{(\lambda )^{k} e^{-\lambda}}{k !}P(X=k)=k!(λ)ke−λ

• 期望：E(X)=λE(X)=\lambdaE(X)=λ
• 方差：D(X)=λD(X) = \lambdaD(X)=λ

例如，某医院平均每小时出生2.5个婴儿（ λ=2.5 ），那么接下来一个小时，会出生几个婴儿？

• 没有婴儿出生（k=0k=0k=0）的概率为：P(X=0)=(2.5)0⋅e−2.50!≈0.082P(X=0)=\frac{(2.5)^{0} \cdot e^{-2.5}}{0 !} \approx 0.082P(X=0)=0!(2.5)0⋅e−2.5≈0.082
• 有1个婴儿出生（k=1k=1k=1）的概率为：P(X=1)=(2.5)1⋅e−2.51!≈0.205P(X=1)=\frac{(2.5)^{1} \cdot e^{-2.5}}{1 !} \approx 0.205P(X=1)=1!(2.5)1⋅e−2.5≈0.205
• 有2个婴儿出生（k=2k=2k=2）的概率为：P(X=2)=(2.5)2⋅e−2.52!≈0.257P(X=2)=\frac{(2.5)^{2} \cdot e^{-2.5}}{2 !} \approx 0.257P(X=2)=2!(2.5)2⋅e−2.5≈0.257
  k012···p0.0820.2050.257···

  通常，柏松分布也叫等待概率，是一种比二项分布应用场景更为丰富的概率模型，在数控、电商优化中也经常能见到它的影子。

5）正态分布（Normal Distribution）（连续型）

在概率论和统计学中，正态分布又叫高斯分布（Gaussian Distribution），其曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形。数学符号为X∼N(μ,σ2)X∼N\left(\mu, \sigma^{2}\right)X∼N(μ,σ2)。

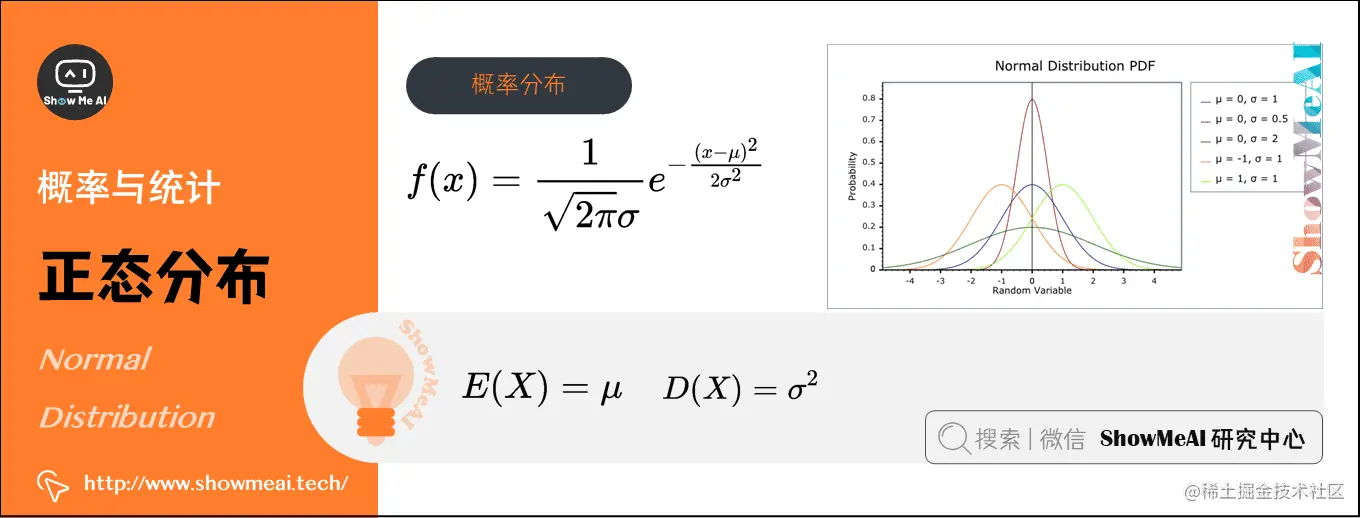若随机变量XXX服从一个数学期望为μ\muμ、方差为σ2\sigma^{2}σ2的正态分布，其概率分布函数：f(x)=12πσe−(x−μ)22σ2f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e {-\frac{(x-\mu){2}}{2 \sigma^{2}}}f(x)=2πσ1e−2σ2(x−μ)2

• 期望：E(X)=μE(X)=\muE(X)=μ
• 方差：D(X)=σ2D(X)=\sigma^{2}D(X)=σ2

6）均匀分布（Uniform Distribution）（连续型）

在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。

均匀分布由两个参数aaa和bbb定义，数学符号为X∼U(a,b)X∼U (a, b)X∼U(a,b)（其中，aaa为数轴上较小值，bbb为数轴上较大值）。

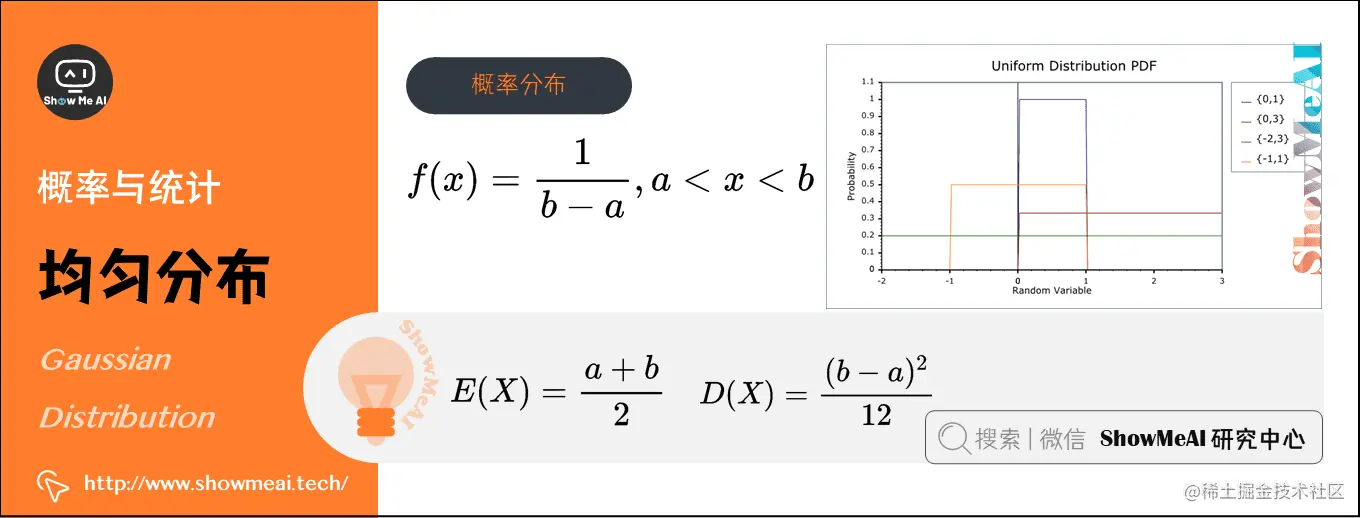其概率分布函数：$f(x)=\frac{1}{b-a} , a

• 期望：E(X)=a+b2E(X)=\frac{a+b}{2}E(X)=2a+b
• 方差：D(X)=(b−a)212D(X) = \frac{(b-a)^{2}}{12}D(X)=12(b−a)2

7）指数分布（Exponential Distribution）（连续型）

在概率论和统计学中，指数分布与其他分布的最大不同之处在于，随机变量XXX指的是不同独立事件发生的时间间隔值，时间越长事件发生的概率指数型增大(减小)，数学符号为X∼E(λ)X∼E(\lambda)X∼E(λ)。

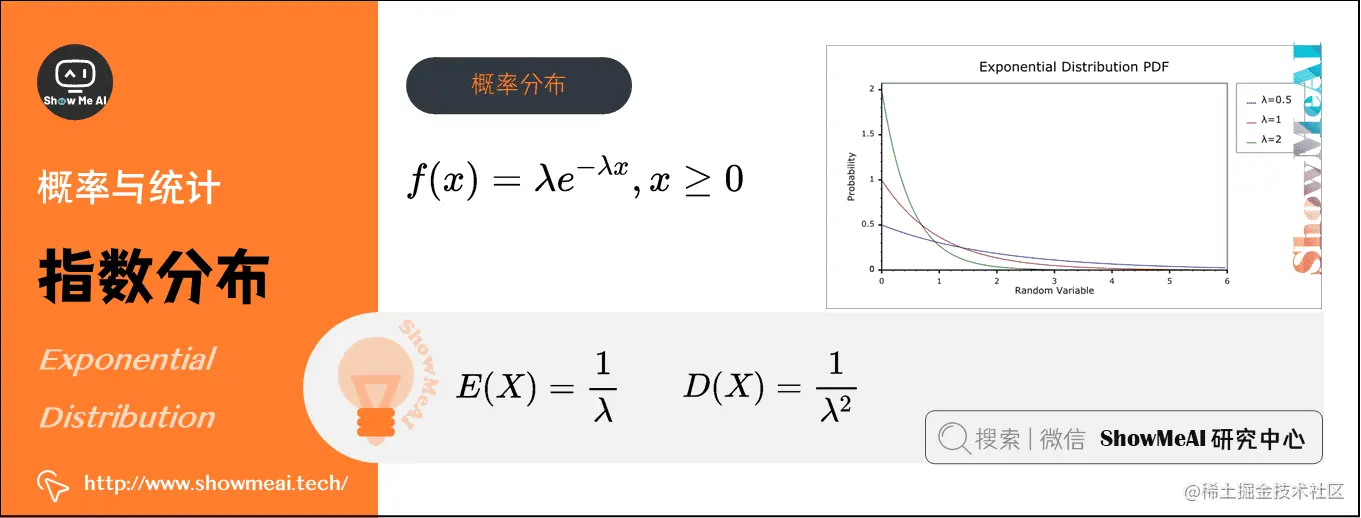指数分布的参数λ\lambdaλ表示单位时间(或单位面积)内随机事件的平均发生次数，其概率分布函数为：f(x)=λe−λx,x≥0f(x) = \lambda e^{-\lambda x}, x\ge 0f(x)=λe−λx,x≥0

• 期望：E(X)=1λE(X)=\frac{1}{\lambda}E(X)=λ1
• 方差：D(X)=1λ2D(X)=\frac{1}{\lambda^{2}}D(X)=λ21

在我们日常的消费领域，通常的目的是求出在某个时间区间内，会发生随机事件的概率有多大。如：银行窗口服务、交通管理、火车票售票系统、消费市场研究报告中被广泛运用。

例如：某医院平均每小时出生2.5个婴儿（ λ=2.5 ）。如果到下一个婴儿出生需要的间隔时间为 t (即时间 t 内没有任何婴儿出生）。

• 间隔15分钟（X=14X=\frac{1}{4}X=41）后才有婴儿出生的概率为：f(14)=2.5e−2.5⋅14≈0.9197f(\frac{1}{4}) = 2.5 e^{-2.5 \cdot \frac{1}{4}} \approx 0.9197f(41)=2.5e−2.5⋅41≈0.9197
• 间隔30分钟（X=12X=\frac{1}{2}X=21）后才有婴儿出生的概率为：f(12)=2.5e−2.5⋅12≈0.7163f(\frac{1}{2}) = 2.5 e^{-2.5 \cdot \frac{1}{2}} \approx 0.7163f(21)=2.5e−2.5⋅21≈0.7163

一些总结：

12.拉格朗日乘子法（Lagrange Multiplier）

在求解最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。

在机器学习的过程中，我们经常遇到在有限制的情况下，最大化表达式的问题。如： maxf(x,y）s.t.g(x,y)=0maxf(x,y）s.t. \quad g(x,y)=0maxf(x,y）s.t.g(x,y)=0

此时我们可以构造L(x,y,λ)=f(x,y)−λ(g(x,y)−c)L(x,y,\lambda )=f(x,y) − \lambda \left ( g(x,y) -c \right )L(x,y,λ)=f(x,y)−λ(g(x,y)−c)，其中λ\lambdaλ称为拉格朗日乘子。接下来要对拉格朗日函数L(x,y,λ)L(x,y,\lambda )L(x,y,λ)求导，令其为0，解方程即可。

以下是图文解释：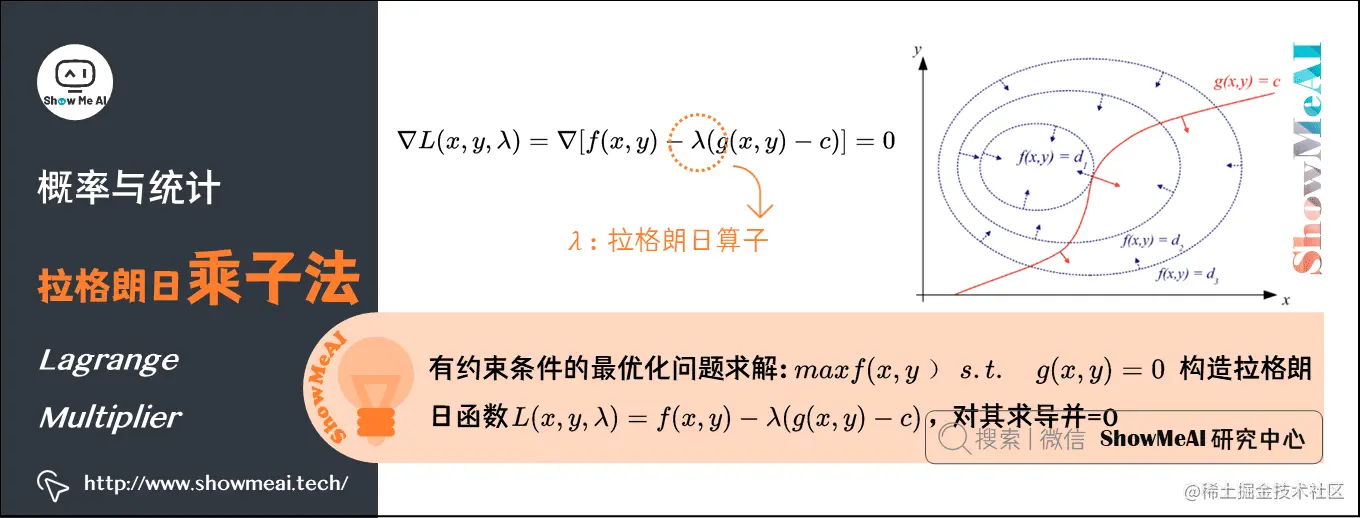

红线标出的是约束g(x,y)=cg(x,y)=cg(x,y)=c的点的轨迹。蓝线是f(x,y)f(x,y)f(x,y)的等高线。箭头表示斜率，和等高线的法线平行，从梯度的方向上来看显然有d1>d2d_{1}>d_{2}d1>d2。

红色的线是约束。如果没有这条约束，f(x,y)f(x,y)f(x,y)的最小值应该会落在最小那圈等高线内部的某一点上。现在加上了约束，正好落在这条红线上的点才可能是满足要求的点。也就是说，应该是在f(x,y)f(x,y)f(x,y)的等高线正好和约束线g(x,y)g(x,y)g(x,y)相切的位置。

对约束也求梯度∇g(x,y)\nabla g(x,y)∇g(x,y)（如图中红色箭头所示），可以看出要想让目标函数f(x,y)f(x,y)f(x,y)的等高线和约束相切g(x,y)g(x,y)g(x,y)，则他们切点的梯度一定在一条直线上。也即在最优化解的时候∇f(x,y)=λ∇g(x,y)−C\nabla f(x,y)=λ \nabla g(x,y)-C∇f(x,y)=λ∇g(x,y)−C，即∇[f(x,y)+λ(g(x,y)−c)]=0,λ≠0\nabla [f(x,y)+λ(g(x,y)−c)]=0,λ≠0∇[f(x,y)+λ(g(x,y)−c)]=0,λ=0。

那么拉格朗日函数L(x,y,λ)=f(x,y)−λ(g(x,y)−c)L(x,y,\lambda )=f(x,y) − \lambda \left ( g(x,y) -c \right )L(x,y,λ)=f(x,y)−λ(g(x,y)−c)在达到极值时与f(x,y)f(x,y)f(x,y)相等，因为F(x,y)F(x,y)F(x,y)达到极值时g(x,y)−cg(x,y)−cg(x,y)−c总等于零。

简单的说，L(x,y,λ)L(x,y,λ)L(x,y,λ)取得最优化解的时候，也就是L(x,y,λ)L(x,y,λ)L(x,y,λ)取极值的时候。此时L(x,y,λ)L(x,y,λ)L(x,y,λ)的导数为0，即∇L(x,y,λ)=∇[f(x,y)−λ(g(x,y)−c)]=0\nabla L(x,y,\lambda )=\nabla \left [ f(x,y) − \lambda \left ( g(x,y) -c \right ) \right ] =0∇L(x,y,λ)=∇[f(x,y)−λ(g(x,y)−c)]=0，可以得出f(x,y)f(x,y)f(x,y)与g(x,y)g(x,y)g(x,y)梯度共线，此时就是在条件约束g(x,y)g(x,y)g(x,y)下，f(x,y)f(x,y)f(x,y)的最优化解。

在支持向量机模型（SVM）的推导中，很关键的一步就是利用拉格朗日对偶性，将原问题转化为对偶问题。

13.最大似然估计（Maximum Likelihood Estimate）

最大概似估计（MLE）是一种粗略的数学期望，指在模型已定、参数θ\thetaθ未知的情况下，通过观测数据估计未知参数θ\thetaθ的一种思想或方法。

最大似然估计的哲学内涵就是：我们对某个事件发生的概率未知，但我们做了一些实验，有过一些对这个事件的经历(经验)，那么我们认为，这个事件的概率应该是能够与我们做的实验结果最吻合。当然，前提是我们做的实验次数应当足够多。

举个例子，假设我们要统计全国人口的身高。首先假设这个身高服从服从正态分布，但是该分布的均值。我们没有人力与物力去统计全国每个人的身高，但是可以通过采样，获取部分人的身高，然后通过最大似然估计来获取上述假设中的正态分布的均值。

最大似然函数的求解思想是：给定样本取值后，该样本最有可能来自参数θ\thetaθ为何值的总体。即：寻找θˉMLE\bar{\theta}_{M LE}θˉMLE使得观测到样本数据的可能性最大。 最大似然函数估计值的一般求解步骤是：

• 写出似然函数

L(θ1,θ2,⋯ ,θn)={∏i=1np(xi;θ1,θ2,⋯ ,θn)∏i=1nf(xi;θ1,θ2,⋯ ,θn)L\left(\theta_{1}, \theta_{2}, \cdots, \theta_{n}\right)=\left{\begin{array}{l} \prod_{i=1}^{n} p\left(x_{i} ; \theta_{1}, \theta_{2}, \cdots, \theta_{n}\right) \ \prod_{i=1}^{n} f\left(x_{i} ; \theta_{1}, \theta_{2}, \cdots, \theta_{n}\right) \end{array}\right.L(θ1,θ2,⋯,θn)={∏i=1np(xi;θ1,θ2,⋯,θn)∏i=1nf(xi;θ1,θ2,⋯,θn)

• 对似然函数取对数
• 两边同时求导数
• 令导数为0解出似然方程

在机器学习中也会经常见到极大似然的影子。比如后面的逻辑斯特回归模型（LR），其核心就是构造对数损失函数后运用极大似然估计。

ShowMeAI相关文章推荐

• 图解线性代数与矩阵论
• 图解概率与统计
• 图解微积分与最优化

ShowMeAI系列教程推荐

• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程