文章目录
前言
Apollo星火计划课程链接如下
星火计划2.0基础课：https://apollo.baidu.com/community/online-course/2
星火计划2.0专项课：https://apollo.baidu.com/community/online-course/12
1. 开放空间规划算法总体介绍
开放空间算法的配置主要在
valet_parking_config.pb.txt
中,分为4个部分：
OPEN_SPACE_ROI_DECIDER
、
OPEN_SPACE_TRAJECTORY_PROVIDER
、
OPEN_SPACE_TRAJECTORY_PARTITION
、
OPEN_SPACE_FALLBACK_DECIDER
。
// /home/yuan/apollo-edu/modules/planning/conf/scenario/valet_parking_config.pb.txt
stage_config:{
stage_type: VALET_PARKING_PARKING
enabled:true
task_type: OPEN_SPACE_ROI_DECIDER
task_type: OPEN_SPACE_TRAJECTORY_PROVIDER
task_type: OPEN_SPACE_TRAJECTORY_PARTITION
task_type: OPEN_SPACE_FALLBACK_DECIDER
1.1 Task: OPEN_SPACE_ROI_DECIDER
根据道路边界，车位边界生成可行驶区域
ps:若可行驶区域里有障碍物，还需要把障碍物的边界考虑进去。
1.2 Task: OPEN_SPACE_TRAJECTORY_PROVIDER
规划粗糙无碰撞轨迹
规划出一条无碰撞的轨迹主要分为以下两个步骤：首先是用混合Astar算法以及RS曲线规划出一条无碰撞的可行轨迹，但是这个轨迹有以下问题：轨迹曲线可能会产生突变，不满足车辆运动学要求。所以需要进一步平滑，这就用到了IAPS/OBCA算法对轨迹进行平滑处理，产生一条无碰撞且满足车辆动力学约束的轨迹。
1.3 Task: OPEN_SPACE_TRAJECTORY_PARTITION
对轨迹进行平滑
这个任务根据对车辆的轨迹是前进的轨迹还是倒车的轨迹进行分割，再根据自车的位置，来决定发送哪一条轨迹以及判断是否需要切换轨迹。
1.4 Task: OPEN_SPACE_FALLBACK_DECIDER
检查规划的轨迹是否与障碍物是否发生碰撞。若发生碰撞，就会进入FALLBACK的状态，规划出一条停车的轨迹，再重新进行路径规划。
2. 基于混合A *的路径规划算法
Astar算法在机器人路径规划领域应用颇多，在这里就不细细展开了，想了解的读者们还请参考这篇文章——
自动驾驶路径规划——A*（Astar）算法
2.1 hybrid A*的简要思想
接下来谈谈Astar算法存在的问题，
可以看到，Astar算法产生的路径并不平滑，不满足车辆的运动学约束。
根据车辆的动力学模型，实际车辆的航向与车辆后轴中心的速度方向是一致的。因此，我们可以把车辆的运动路径等效为后轴中心点的一段段不同曲率半径的弧线组成，如下图所示。
通过车辆的前轮转角，可以计算出车辆后轴的转弯半径。
tan
(
δ
)
=
L
R
\tan (\delta ) = \frac{L}{R}
tan(δ)=RL 我们可以对前轮转角进行采样，不同的前轮转角对应了不同的转弯半径，每个采样周期内，行驶一段固定长度的弧长，这样我们就可以得到下图所示的平滑路径。 如此一来，Astar原本的栅格地图对于现在的轨迹并不适用，所以需要新增
θ
\theta
θ航向角这个变量去描述车辆的轨迹，即原本的二维节点
(
x
,
y
)
(x,y)
(x,y)变为了三维节点
(
x
,
y
,
θ
)
(x,y,\theta)
(x,y,θ)。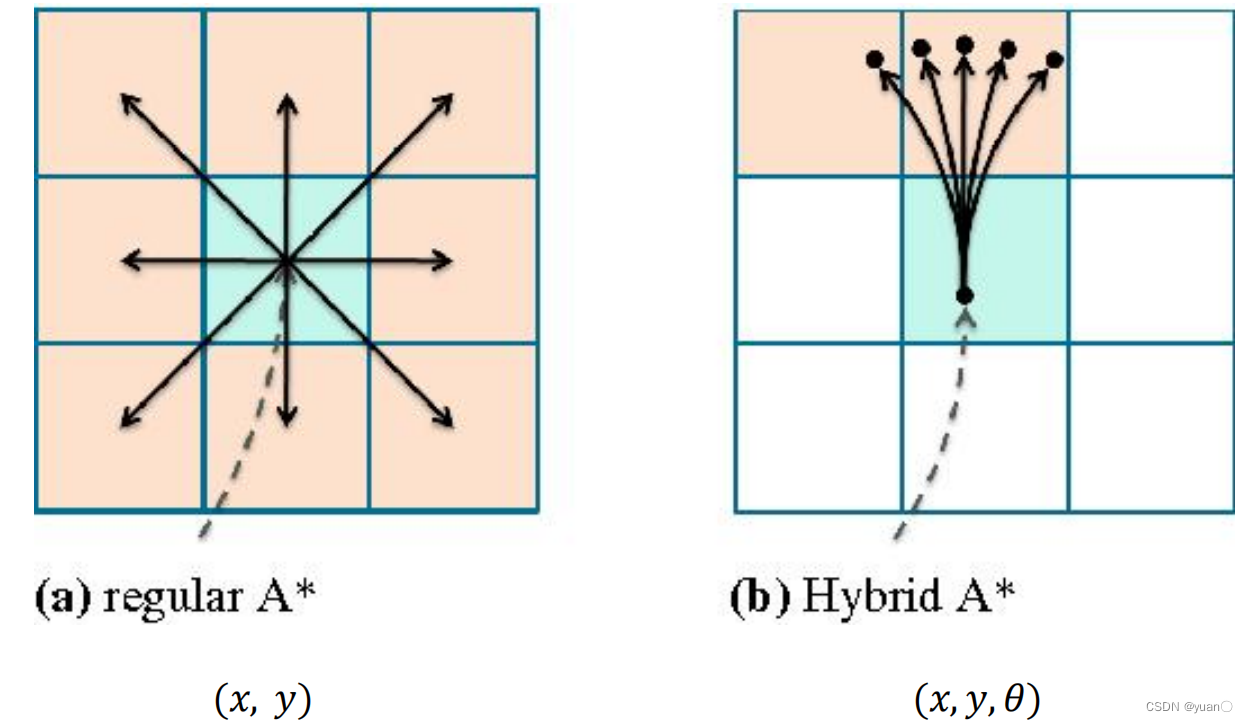 下面是Apollo中3维节点的格式。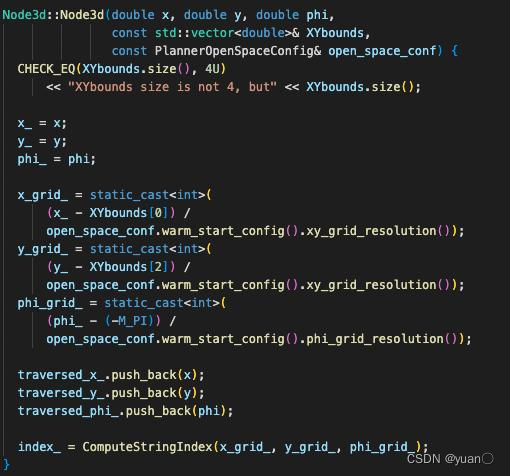
其中
x_grid
、
y_grid
、
phi_grid
分别是
(
x
,
y
,
θ
)
(x,y,\theta)
(x,y,θ)的索引，即
(
x
,
y
,
θ
)
(x,y,\theta)
(x,y,θ)方向上的长度除以精度。通过三个索引组成的字符串是否相同，来判断节点是否遍历过了。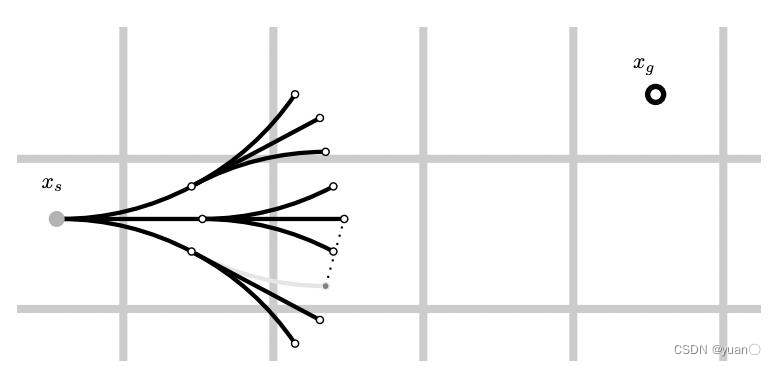 因为单纯通过搜索难以到达终点，所以我们需要对路径节点进行解析扩展。
2.2 RS曲线
1990 Optimal paths for a car that goes both forwards and backwards. J. A. Reeds, L. A. Shepp. Pacific J. Math. 145(2): 367-393 (1990).
1990年，ReedShepp曲线被J. A. Reeds, L. A. Shepp提出：给定起点和终点，可以通过固定半径的圆弧和直线进行连接。圆弧和直线的组合一共有48种，他们证明，任意的最短路径的组合都在48种组合之中。他们还给出了48种组合的解析解及其求解方法。
其中，
C
C
C代表圆弧，
S
S
S代表直线，|代表方向的变换
不过这种方法是无法判断障碍物的，所以需要有个障碍物检测的步骤，将与障碍物碰撞的路径过滤掉。
2.3 Apollo中Hybrid A*算法的求解过程
下面是Apollo中Hybrid A*算法的求解过程。
代码片段
// /home/yuan/apollo-edu/modules/planning/open_space/coarse_trajectory_generator/hybrid_a_star.cc
grid_a_star_heuristic_generator_->GenerateDpMap(ex, ey, XYbounds_,
obstacles_linesegments_vec_);
ADEBUG <<"map time "<<Clock::NowInSeconds()- map_time;// load open set, pq
open_set_.emplace(start_node_->GetIndex(), start_node_);
open_pq_.emplace(start_node_->GetIndex(), start_node_->GetCost());// Hybrid A* begins
size_t explored_node_num =0;double astar_start_time =Clock::NowInSeconds();double heuristic_time =0.0;double rs_time =0.0;while(!open_pq_.empty()){// take out the lowest cost neighboring nodeconst std::string current_id = open_pq_.top().first;
open_pq_.pop();
std::shared_ptr<Node3d> current_node = open_set_[current_id];// check if an analystic curve could be connected from current// configuration to the end configuration without collision. if so, search// ends.constdouble rs_start_time =Clock::NowInSeconds();if(AnalyticExpansion(current_node)){break;}constdouble rs_end_time =Clock::NowInSeconds();
rs_time += rs_end_time - rs_start_time;
close_set_.emplace(current_node->GetIndex(), current_node);for(size_t i =0; i < next_node_num_;++i){
std::shared_ptr<Node3d> next_node =Next_node_generator(current_node, i);// boundary check failure handleif(next_node ==nullptr){continue;}// check if the node is already in the close setif(close_set_.find(next_node->GetIndex())!= close_set_.end()){continue;}// collision checkif(!ValidityCheck(next_node)){continue;}if(open_set_.find(next_node->GetIndex())== open_set_.end()){
explored_node_num++;constdouble start_time =Clock::NowInSeconds();CalculateNodeCost(current_node, next_node);constdouble end_time =Clock::NowInSeconds();
heuristic_time += end_time - start_time;
open_set_.emplace(next_node->GetIndex(), next_node);
open_pq_.emplace(next_node->GetIndex(), next_node->GetCost());}}}
第一步基于动态规划算法求解每个二维节点的代价值，将其作为混合Astar的一个启发函数
GenerateDpMap
。
grid_a_star_heuristic_generator_->GenerateDpMap(ex, ey, XYbounds_,
obstacles_linesegments_vec_);
接着定义了两个集合开放集合
open_set_
闭合集合
close_set_
以及一个优先队列
open_pq_
.保存开放集合，并将起点加入开放集中。
// load open set, pq
open_set_.emplace(start_node_->GetIndex(), start_node_);
open_pq_.emplace(start_node_->GetIndex(), start_node_->GetCost());
close_set_.emplace(current_node->GetIndex(), current_node);
再定义一个whlie循环，并在每次循环时弹出代价值最小的节点。
while(!open_pq_.empty()){// take out the lowest cost neighboring nodeconst std::string current_id = open_pq_.top().first;
open_pq_.pop();
std::shared_ptr<Node3d> current_node = open_set_[current_id];
在循环中，会对当前节点的状态到目标节点的状态是否有一个无碰撞的RS曲线（用
AnalyticExpansion
函数进行判断），若找到解析解，则直接退出循环
if(AnalyticExpansion(current_node)){break;}
若没有，则将该节点加入close集之中
close_set_.emplace(current_node->GetIndex(), current_node);
并对节点进行拓展(
Next_node_generator
)，访问其相邻节点。并对拓展节点进行碰撞检测。
for(size_t i =0; i < next_node_num_;++i){
std::shared_ptr<Node3d> next_node =Next_node_generator(current_node, i);// boundary check failure handleif(next_node ==nullptr){continue;}// check if the node is already in the close setif(close_set_.find(next_node->GetIndex())!= close_set_.end()){continue;}// collision checkif(!ValidityCheck(next_node)){continue;}
若节点没有被遍历过，也没有和障碍物发生碰撞，则将其加入open集中，并计算该节点的代价值（
CalculateNodeCost
）
if(open_set_.find(next_node->GetIndex())== open_set_.end()){
explored_node_num++;constdouble start_time =Clock::NowInSeconds();CalculateNodeCost(current_node, next_node);constdouble end_time =Clock::NowInSeconds();
heuristic_time += end_time - start_time;
open_set_.emplace(next_node->GetIndex(), next_node);
open_pq_.emplace(next_node->GetIndex(), next_node->GetCost());}
Hybrid Astar + ReedShepp曲线规划效果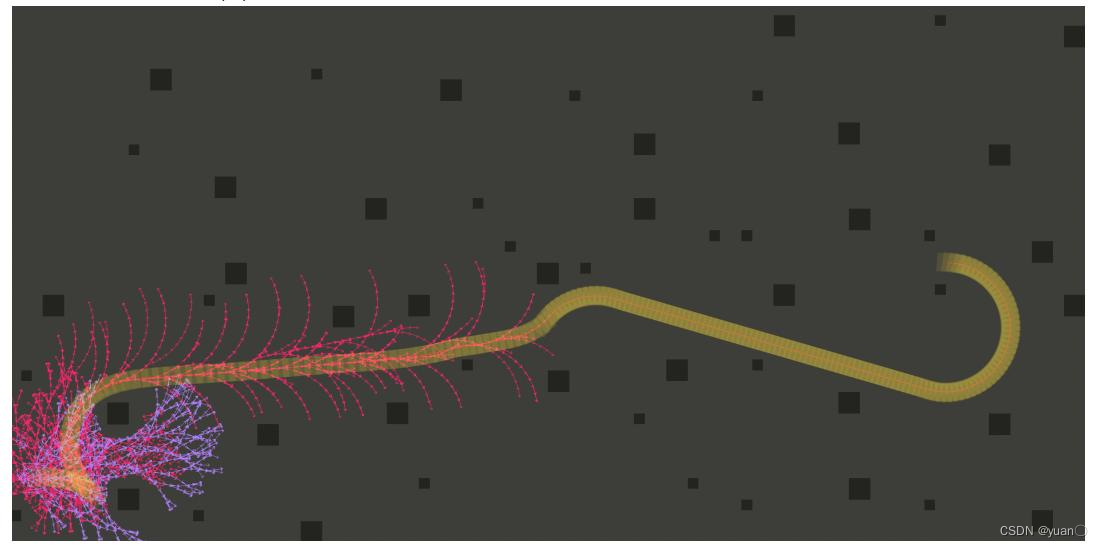
可以看到由于部分轨迹并不平滑，所以需要平滑算法进一步的平滑。
3. 基于OBCA的轨迹规划算法
3.1 OBCA算法的特点
OBCA算法
• OBCA算法是基于模型预测控制（MPC）建立模型，并用优化算法进行求解
• 可以加入障碍物约束
• 可以实现横纵向联合规划
• 可以产生满足车辆运动学约束的轨迹
参考文献
1.TDR-OBCA: A Reliable Planner for Autonomous Driving in Free-SpaceEnvironment https://arxiv.org/abs/2009.11345（Apollo改进）
2.Optimization-Based Collision Avoidance https://arxiv.org/abs/1711.03449（OBCA原论文）
3.2 模型预测控制MPC
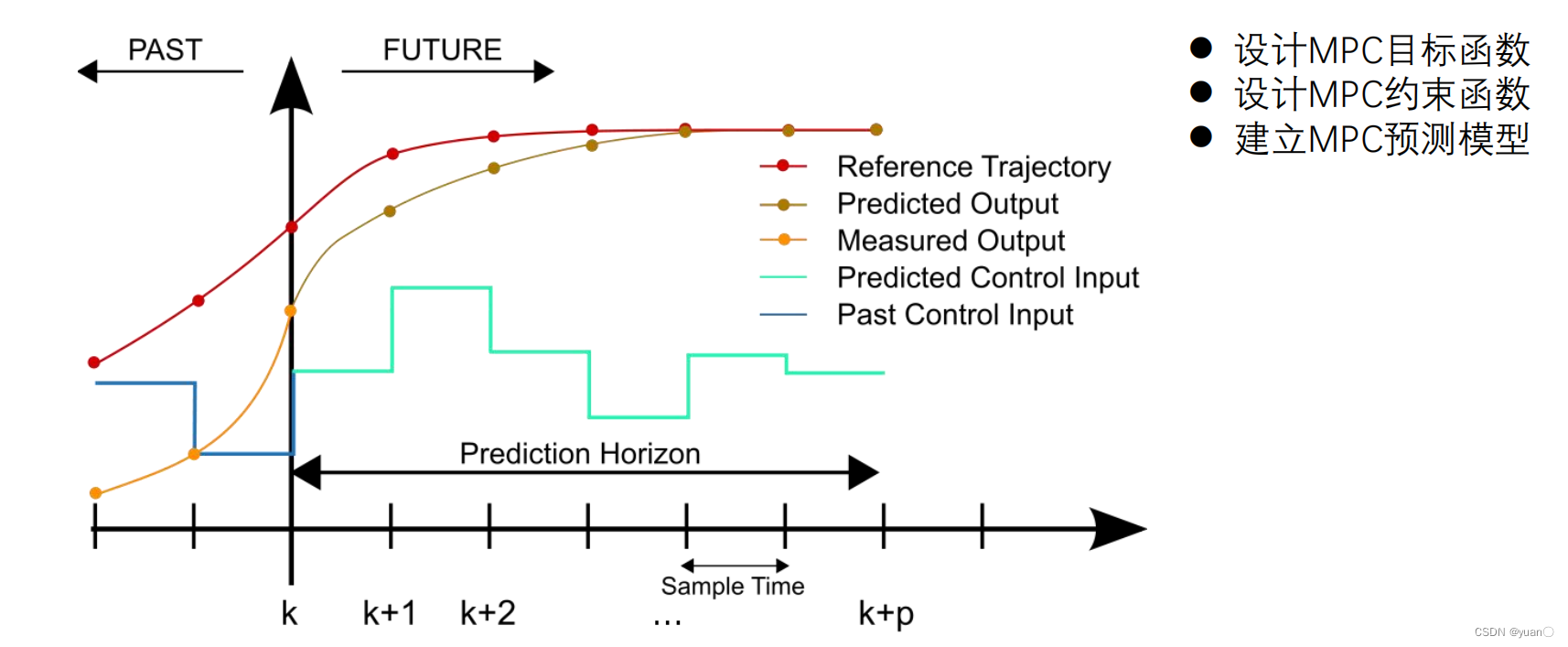
模型预测控制会通过一个采样时间将未来时域离散成多断，在给定控制模型和参考值曲线，计算使预测输出与参考输出最接近的输入序列，并将输入的第一个分量作用于系统.
因为模型预测控制问题最后还是要转化为一个优化问题，所以需要设计目标函数与约束函数；同时MPC也是一个预测问题，所以需要建立预测模型。
3.3 模型预测控制状态方程
接下来看看MPC模型预测控制状态方程是如何建立的。首先定义自车状态变量，包括自车在第
k
k
k时间的坐标
(
x
,
y
)
(x,y)
(x,y),速度
v
v
v,航向角
ϕ
\phi
ϕ。
x
(
k
)
=
(
x
x
(
k
)
x
y
(
k
)
x
v
(
k
)
x
ϕ
(
k
)
)
x(k) = \left( {\begin{array}{ccccccccccccccc}{{x_x}(k)}\\{{x_y}(k)}\\{{x_v}(k)}\\{{x_\phi }(k)}\end{array}} \right)
x(k)=xx(k)xy(k)xv(k)xϕ(k) 以及输入
u
k
u_k
uk,
u
k
u_k
uk包括了主车的前轮转角
δ
(
k
)
\delta (k)
δ(k)与加速度
a
(
k
)
]
a(k)]
a(k)]。
u
(
k
)
=
[
δ
(
k
)
,
a
(
k
)
]
T
u(k) = {[\delta (k),a(k)]^T}
u(k)=[δ(k),a(k)]T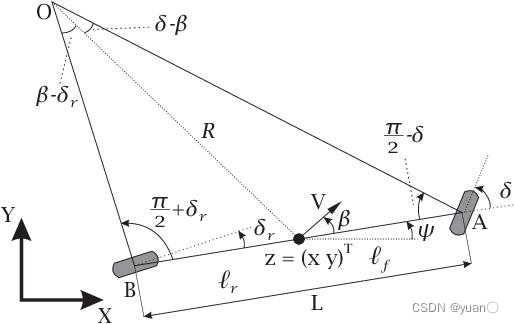 运动控制模型是车辆的二自由度运动模型，下列式子为第
k
+
1
k+1
k+1时间与第
k
k
k时间的状态对应关系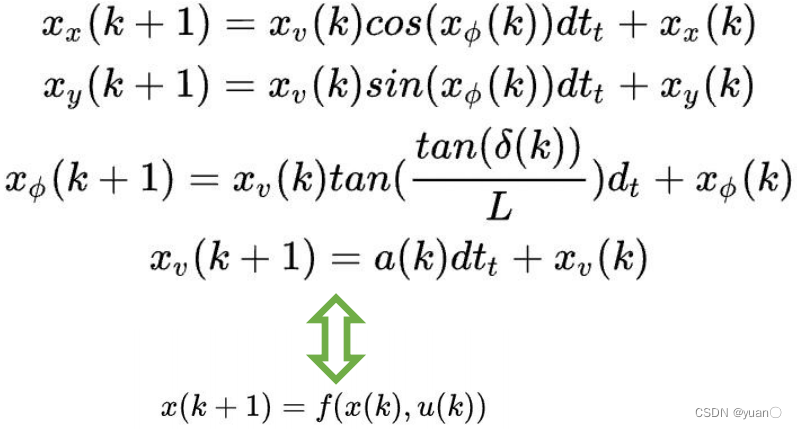： 在控制算法中，我们需要的是
u
u
u的第一个分量；在轨迹算法中，我们需要将所有状态作为最后输出的轨迹。
3.4 利用超平面构建障碍物约束
OBCA算法主要考虑了障碍物的约束，且是利用超平面去构造障碍物的约束。
构造完之后，通过如下向量约束进行表示：
- 当 x 1 < x 2 x_1 < x_2 x1<x2时, A m = ( − a 1 ) b m = b X = ( x y ) A m X ≤ b m \begin{array}{c}{A_m} = \left( {\begin{array}{ccccccccccccccc}{ - a}\1\end{array}} \right)\{b_m} = b\X = \left( {\begin{array}{ccccccccccccccc}x\y\end{array}} \right)\{A_m}X \le {b_m}\end{array} Am=(−a1)bm=bX=(xy)AmX≤bm
- 当 x 1 > x 2 x_1 > x_2 x1>x2时 A m = ( a − 1 ) b m = − b X = ( x y ) A m X ≤ b m \begin{array}{c}{A_m} = \left( {\begin{array}{ccccccccccccccc}a\{ - 1}\end{array}} \right)\{b_m} = - b\X = \left( {\begin{array}{ccccccccccccccc}x\y\end{array}} \right)\{A_m}X \le {b_m}\end{array} Am=(a−1)bm=−bX=(xy)AmX≤bm
通过求解
A
A
A和
B
B
B的坐标，即可以得到
A
m
A_m
Am和
b
m
b_m
bm.
对于障碍物，其在空间中可以用四条边进行描述，障碍物约束可以表示为：
其中
A
m
=
{
A
a
b
A
b
c
A
d
c
A
d
a
,
b
m
=
{
b
a
b
b
b
c
b
d
c
b
d
a
{A^m} = \left\{ {\begin{array}{ccccccccccccccc}{{A_{ab}}}\\{{A_{bc}}}\\{{A_{dc}}}\\{{A_{da}}}\end{array}} \right.,{b^m} = \left\{ {\begin{array}{ccccccccccccccc}{{b_{ab}}}\\{{b_{bc}}}\\{{b_{dc}}}\\{{b_{da}}}\end{array}} \right.
Am=⎩⎨⎧AabAbcAdcAda,bm=⎩⎨⎧babbbcbdcbda
自车的表述方式也是类似的，也可以用超平面进行构造。自车占用空间
B
\mathbb{B}
B可以表示为：
B
:
=
{
e
:
G
e
≤
g
}
\mathbb{B}: = \{ e:Ge \le g\}
B:={e:Ge≤g} 式中：
G
=
[
1
0
−
1
0
0
1
0
−
1
]
,
g
=
[
1
2
ω
2
l
2
ω
2
]
G = \left[ {\begin{array}{ccccccccccccccc}1\\0\\{ - 1}\\0\end{array}\begin{array}{ccccccccccccccc}0\\1\\0\\{ - 1}\end{array}} \right],g = \left[ {\begin{array}{ccccccccccccccc}{\frac{1}{2}}\\{\frac{\omega }{2}}\\{\frac{l}{2}}\\{\frac{\omega }{2}}\end{array}} \right]
G=10−10010−1,g=212ω2l2ω 自车在第
k
k
k时间状态
E
\mathbb{E}
E所占用的空间可以通过旋转和平移得到：
R
(
x
(
k
)
)
R(x(k))
R(x(k))为旋转矩阵，
t
(
x
(
k
)
)
t(x(k))
t(x(k))为平移矩阵。
若要满足主车占用空间和障碍物空间无碰撞，则障碍物的占用空间和主车的占用空间的交集为空：
同时还需定义主车和障碍物最小距离（
d
i
s
t
dist
dist是主车向量延任意方向平移与障碍物发生重合时，范数最小的函数，简单的说，就是两个集合间最小的距离）：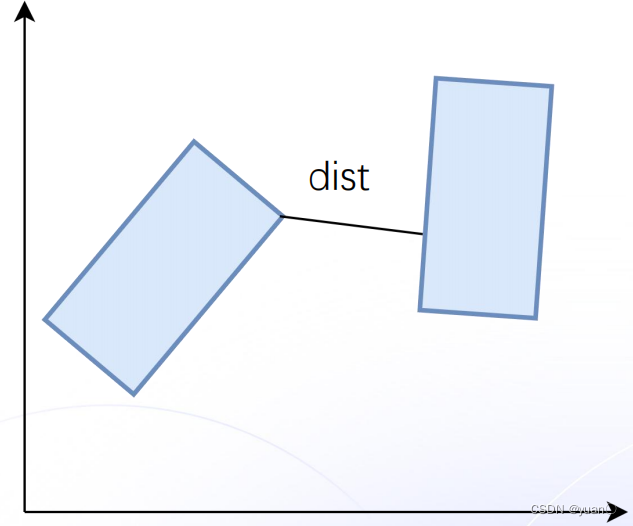
如果要保证和障碍物距离>d_min则有：
λ
m
，
μ
m
{\lambda _m}，{\mu _m}
λm，μm为拉格朗日乘数。
接下来看看这些式子是如何得到的。首先原问题为主车在
E
\mathbb{E}
E的位置距离障碍物的距离。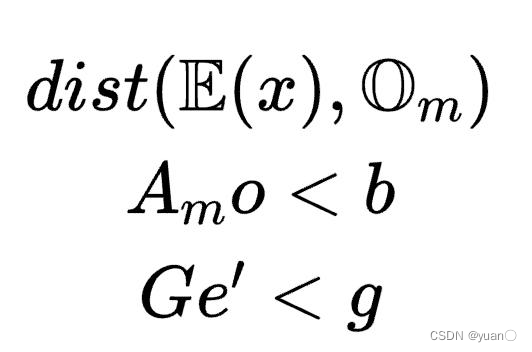
e
e
e为自车占用空间
E
(
x
)
\mathbb{E}(x)
E(x)里任意的一个点，
o
o
o为障碍物占用空间
O
m
\mathbb{O}_m
Om里的任意一个点，分别满足如下约束：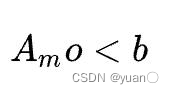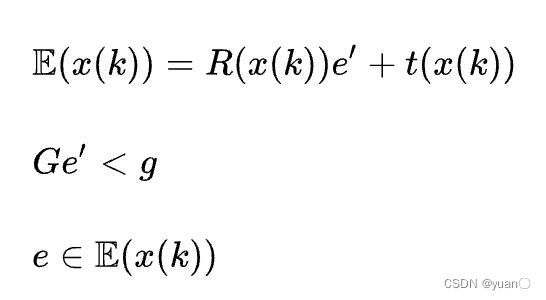
自车占用空间
E
(
x
)
\mathbb{E}(x)
E(x)里任意的一个点，
o
o
o为障碍物占用空间
O
m
\mathbb{O}_m
Om里的任意一个点之间最小的欧几里得距离（
e
e
e,
o
o
o构成的范数）大于
d
m
i
n
d_{min}
dmin，则有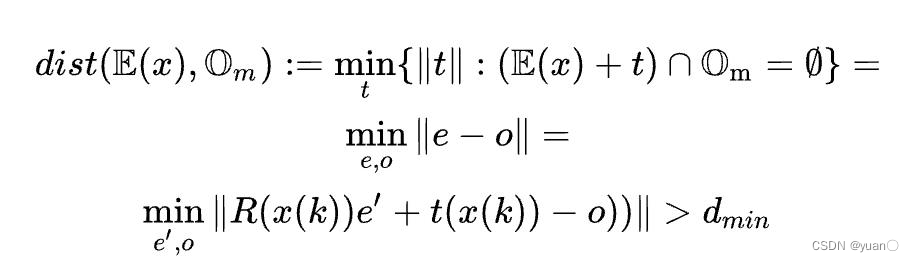： 这里将
e
e
e变为
R
(
x
(
k
)
)
e
′
+
t
(
x
(
k
)
)
R(x(k))e' + t(x(k))
R(x(k))e′+t(x(k))，
e
′
e'
e′为原点占用空间里的一个点，通过旋转和平移得到
e
e
e点的位置。
由于范数中包含两个优化变量，不好计算。所以引入新的优化变量
w
w
w和约束。
w
=
R
(
x
(
k
)
)
e
′
+
t
(
x
(
k
)
)
−
o
w = R(x(k))e' + t(x(k)) - o
w=R(x(k))e′+t(x(k))−o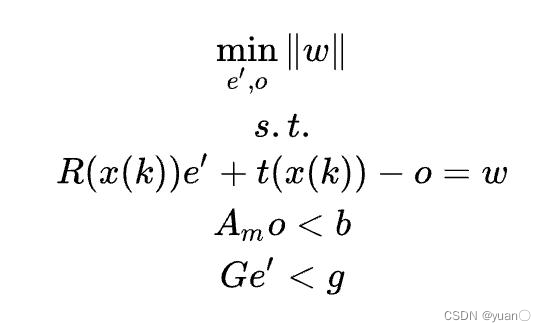 于是便将问题转化为了求解当
w
w
w的二范数最小时，
e
′
e'
e′和
o
o
o的取值。然而，在凸优化的问题里，这类有条件的极值问题是不大好研究的。所以需要将有条件的极值问题转化为无条件的极值问题。
我们将有条件的极值问题称为原问题，如下表述：
其拉格朗日函数为：
通过拉格朗日函数，可以将有约束条件的问题转化为无约束条件的对偶问题。
接着，把
L
(
x
,
λ
,
υ
)
L(x,\lambda ,\upsilon )
L(x,λ,υ)中的
λ
,
υ
\lambda ,\upsilon
λ,υ看作常量，求解在
x
x
x定义域内对拉格朗日函数取极小值，就获得了拉格朗日的对偶函数（拉格朗日函数在
x
x
x定义域内的下确界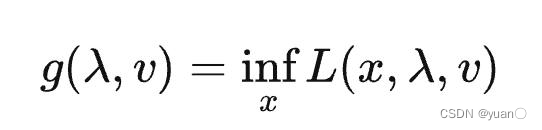）： 原问题的对偶问题即为拉格朗日函数的对偶函数取极大值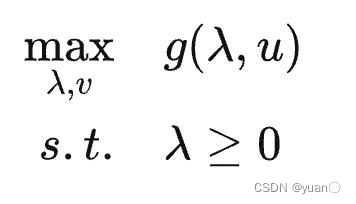： 我们一般将原问题定义为
p
∗
p^*
p∗,对偶问题定义为
d
∗
d^*
d∗。
min
x
f
0
(
x
)
=
p
∗
max
λ
,
υ
g
(
λ
,
υ
)
=
d
∗
\begin{array}{l}\mathop{\min }\limits_x {f_0}(x) = {p^ * }\\ \mathop{\max }\limits_{\lambda ,\upsilon } g(\lambda ,\upsilon ) = {d^*}\end{array}
xminf0(x)=p∗λ,υmaxg(λ,υ)=d∗
对于凸优化问题，
p
∗
≥
d
∗
{p^ * } \ge {d^*}
p∗≥d∗
再回到原问题：
引入拉格朗日变量
μ
，
λ
，
z
μ，λ，z
μ，λ，z，则其拉格朗日对偶函数为
3.5 MPC约束设计
- 规划的轨迹和障碍物保持一定距离
- 规划的轨迹起点和终点满足给定的状态
- 状态的迭代满足运动学约束：
- 状态量满足规划极限（ x x x, y y y, v v v的值有所限制，航向角可以任意取值）
- 输入量满足车辆极限（最大的加速度以及横摆角速度）
3.6 MPC目标函数设计
MPC的目标函数是对预测时域每个状态
x
(
k
)
x(k)
x(k)的损失函数的求和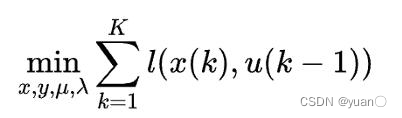： 损失函数有以下要求：
- 跟踪参考路径变化： x ( k ) → x r e f x(k) \to {x_{ref}} x(k)→xref
- 加速度尽可能小： u ( k ) ↓ u(k) \downarrow u(k)↓
- 第一个输入分量和当前状态输入尽可能接近： u ( 1 ) → u ~ u(1) \to \tilde u u(1)→u~
- 输入量变化率尽可能小： u ˙ ( k ) ↓ \dot u(k) \downarrow u˙(k)↓
下式为
c
o
s
t
cost
cost代价函数，每一项
c
o
s
t
cost
cost都用二范数进行表示。
3.7 OBCA算法（DISTANCE_APPROACH_IPOPT_FIXED_TS）
如此，可以将OBCA的规划问题转化为非线性问题，用IPOPT求解。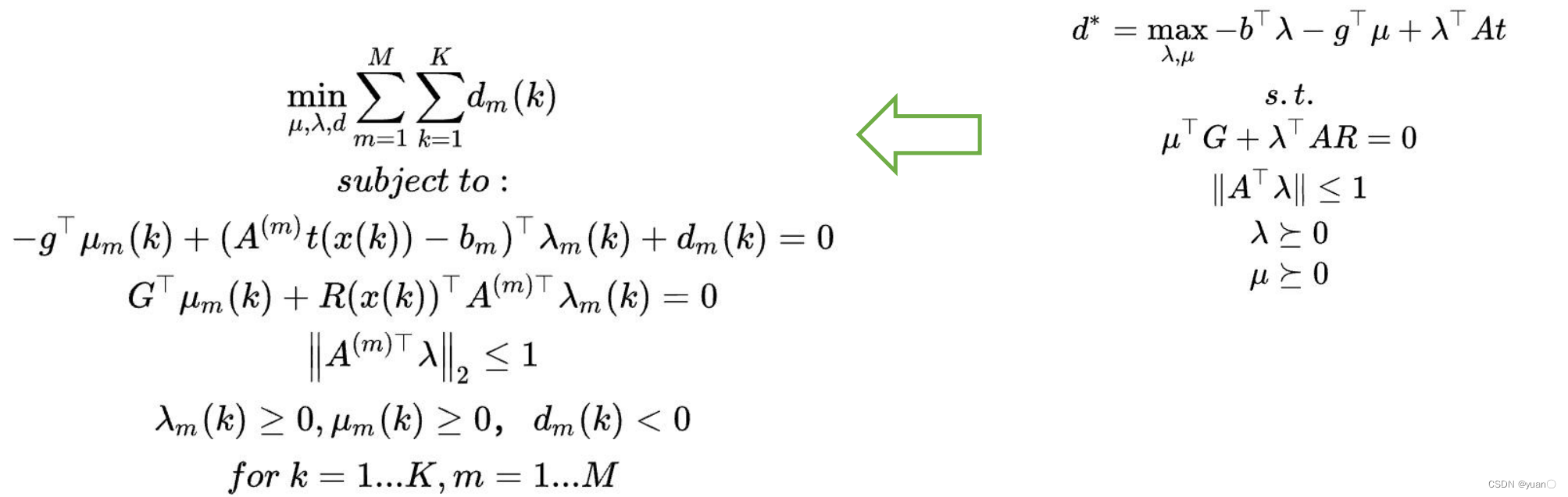
对偶变量也需初始化，将极大值问题转化为极小值问题，利于求解。
除了OBCA（DISTANCE_APPROACH_IPOPT_FIXED_TS）外，Apollo还有一些衍生算法。
3.8 OBCA 衍生算法
3.8.1 采样时间可变（ DISTANCE_APPROACH_IPOPT ）
原来的采样时间为
t
S
t_S
tS,无论怎么优化都会在最后时刻才达到终点。于是增加一个采样时间系数
t
(
k
)
t(k)
t(k)，采样时间就变为
t
s
∗
t
(
k
)
t_s*t(k)
ts∗t(k)，从而缩短了采样的时间。
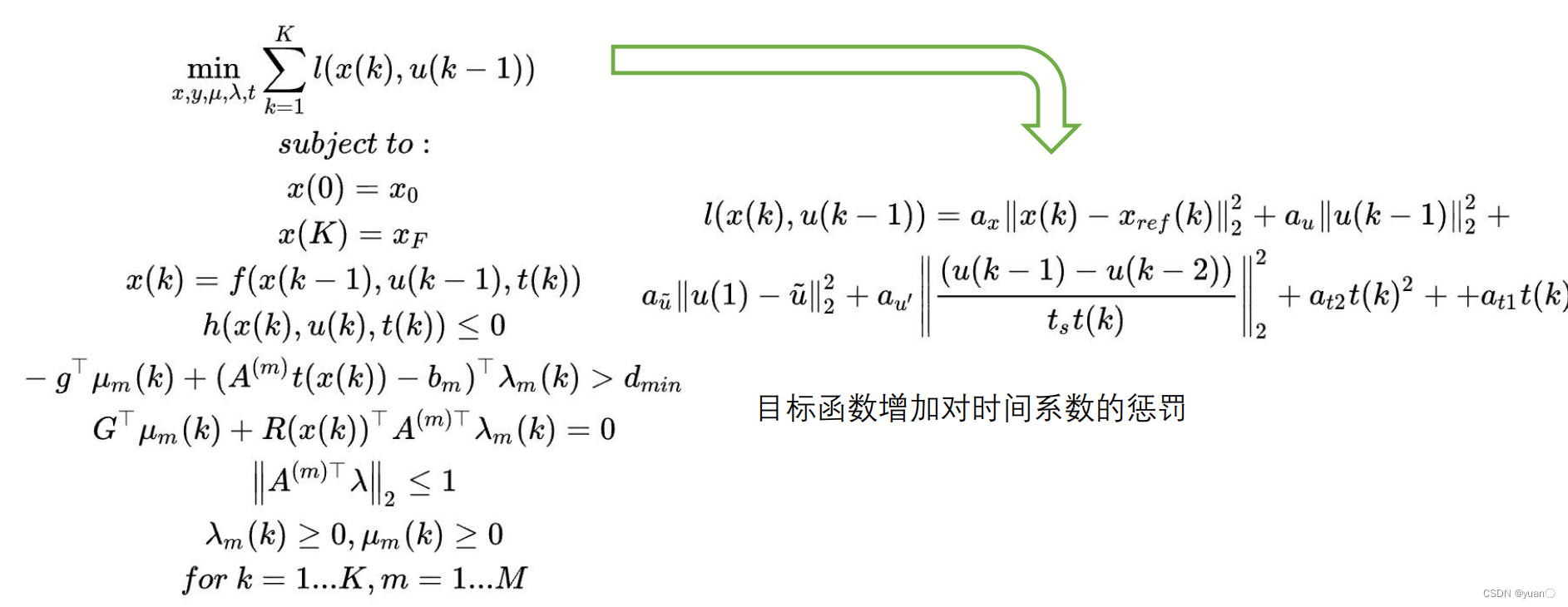
3.8.2 终点松弛（ DISTANCE_APPROACH_IPOPT_RELAX_END）
4. 基于DL-IAPS的路径规划算法
虽然OBCA算法通过凸优化的强对偶性很好地解决了在开放空间和障碍物的无碰撞的约束，但算法的鲁棒性与效率较低。因此Apollo设计了以一种横纵向解耦合算法。
横纵向解耦的开放空间轨迹规划算法
Zhou J, He R, Wang Y, et al. Dl-iaps and pjso: A path/speed decoupled trajectory optimization and its application in autonomous driving[J]. arXiv preprint arXiv:2009.11135, 2020.
DL-IAPS算法是分段式的路径规划算法。OBCA算法是依据完整的路径进行平滑，而DL-IAPS算法则是根据混合
A
∗
A^*
A∗产生的路径，判断轨迹是前进还是倒车后退，进行分段平滑，同时保证平滑后的路径不会与障碍物发生碰撞并满足最大的曲率约束。
该算法采样的速度规划算法为PJSO算法，与基于二次规划的速度规划算法是比较类似的（
Apollo星火计划学习笔记——Apollo速度规划算法原理与实践）。在DL-IAPS规划出的路径上分别对位置、速度以及加速度进行采样，并通过二次规划进行求解。
4.1 DL-IAPS （Dual Loop Iterative Anchoring Path Smoothing）
算法伪代码
主要包含了两层循环，外层循环是处理和障碍物碰撞约束的一个循环，内层循环是路径平滑的循环。对于开放空间的路径规划问题，难点在于障碍物约束的求解。
DL-IAPS类似于参考线的平滑算法（Apollo星火计划学习笔记——参考线平滑算法解析及实现（以U型弯道场景仿真调试为例）），但在每一个循环之后，会将结果和所有的障碍物进行碰撞检查，若发生碰撞，则将boundingbox矩形框调小，再次进行平滑，如此迭代，直到能满足约束。
参考线一般来自于地图的车道线，所以其曲率不大，同时由于参考线平滑的点的数目比较多，对实时性的要求比较高，参考线平滑算法采用了不考虑曲率约束的基于二次规划的平滑算法。
但对于开放空间的路径规划而言，得到的参考路径来自于混合Astar的搜索结果，参考路线本身的曲率是比较大的，因此需要把曲率约束考虑进去。
Apollo采用了一种SQP序列二次规划算法来解决非线性的约束问题。
首先对约束函数进行线性化，将其泰勒展开：
保留一次项，得到下式
很明显，这里需要知道约束函数在
X
0
X_0
X0的值
F
(
X
0
)
F({X_0})
F(X0)以及导数值
F
′
(
X
0
)
F'({X_0})
F′(X0)。在序列二次规划中，可以利用上一次平滑的结果，作为这次的参考点，同时对优化点增加一个可信区间约束（下式），避免两次规划的点之间约束过远。
将上述问题简化为二次规划问题。其目标函数包含两项，第一项为相邻平滑度的代价，第二项为曲率约束的松弛变量。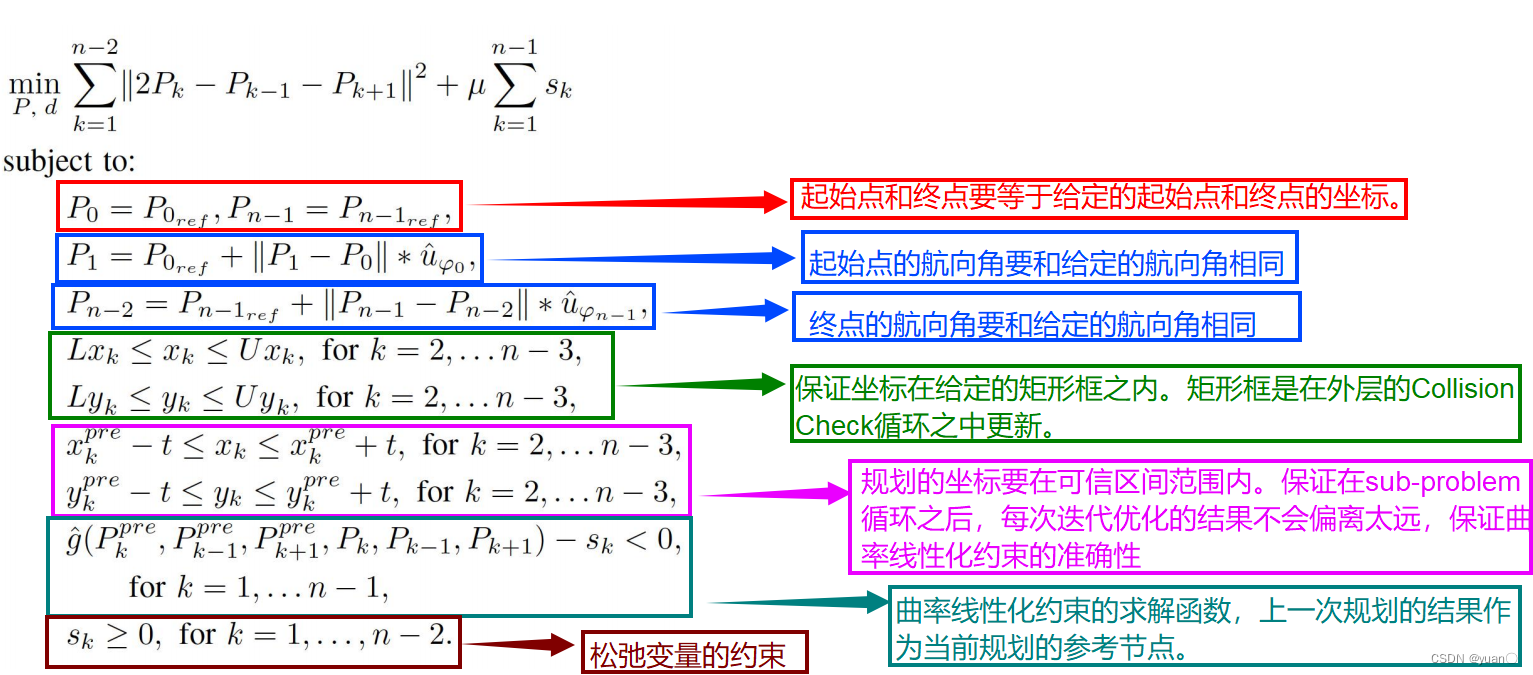
下图为Open Space Planner的整体架构。首先通过Open Space Decider确定可行驶区域，再利用混合Astar算法搜索出一条粗糙的轨迹。再利用DL-IAPS算法对得到的粗糙轨迹进行曲率平滑，得到一条满足曲率约束且无碰撞的路径。接着对平滑后的路径进行速度规划，最后生成一条轨迹。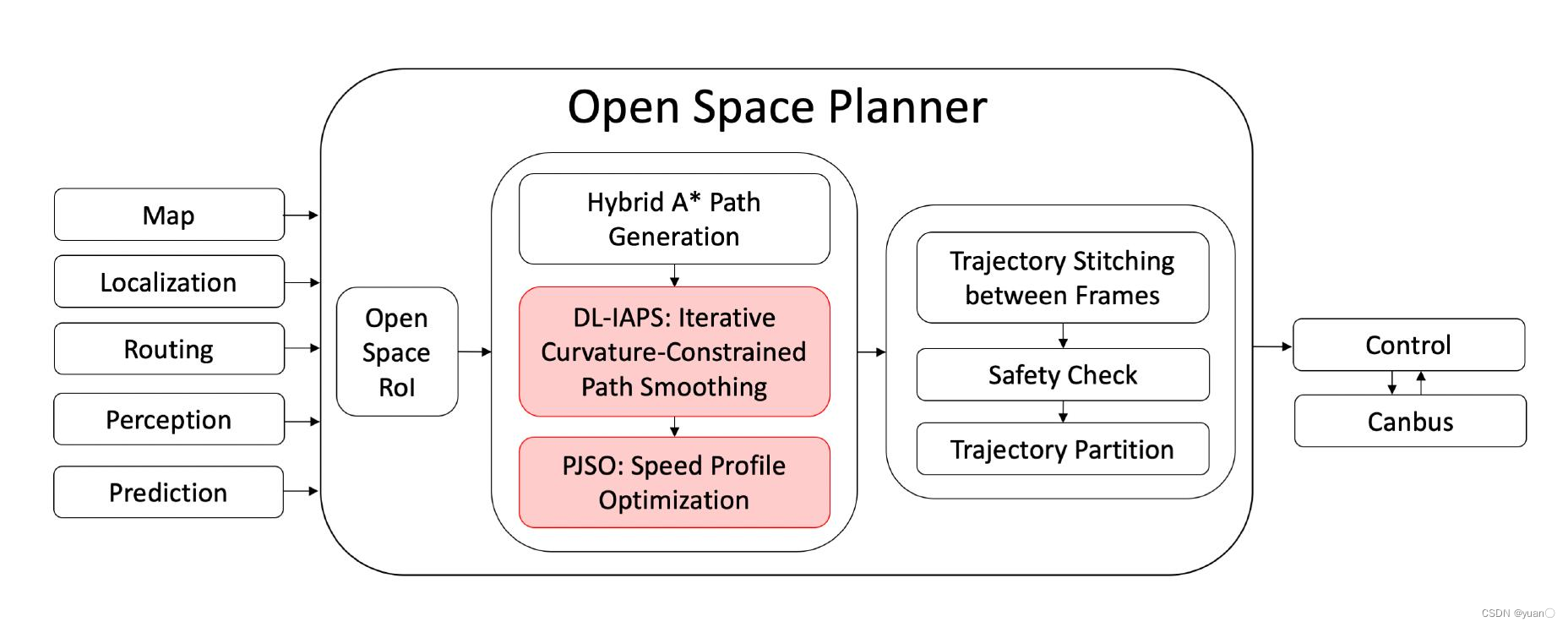
各算法间的比较。改进算法具有加大效率优势。
5. 开放空间规划算法实践
云实验地址——Apollo规划之开放空间规划
首先启动DreamView
bash scripts/bootstrap.sh
模式选择
Mkz Standard Debug
，地图选择
ApolloVirutal Map
，打开
Sim_Control
模式，打开
PNCMonitor
，等待屏幕中间区域出现Mkz车模型和地图后即表示成功进入仿真模式。
点击左侧Tab栏Module Controller，启动Planning,Prediction，Routing，TaskManager模块，如果需要录制数据则打开Recorder模块。
5.1 自主泊车场景实践
模块启动完成后，找到地图中间的停车位，分别选择停车位前道路上一个点和其中的一个停车位作为终点，点击Send Request，发布路由请求。在右侧的pnc monitor中可以看到设置的可行驶区域边界，warm start曲线是规划的粗糙的轨迹(混合Astar)，smooth是平滑后的曲线.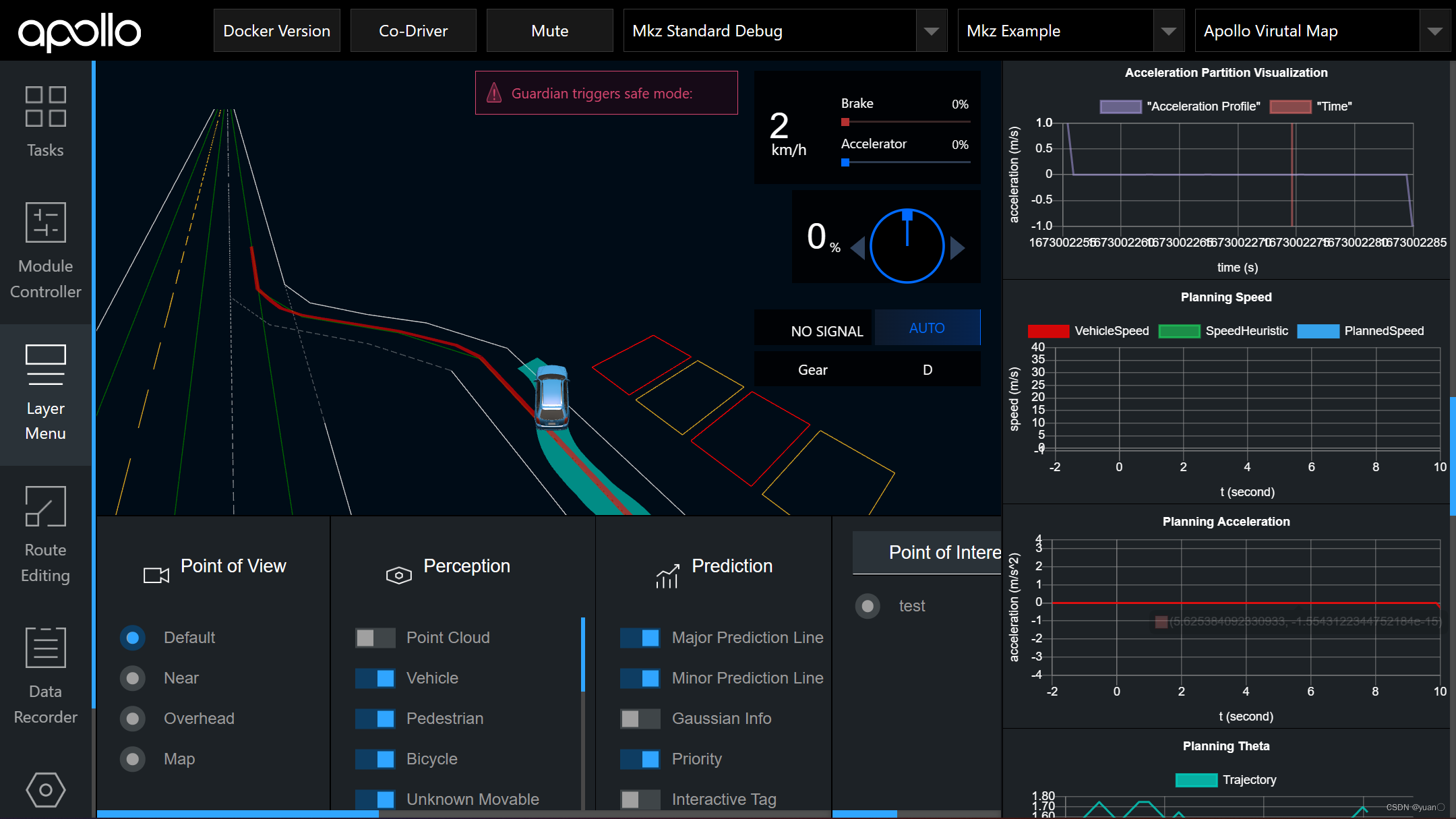
自主泊车经过以下三个阶段。
OBCA算法的轨迹
调高
planning_config.pb.txt
中
distance approach
算法跟随
warm start
路径的权重
weight_x
,
weight y
,
weight_phi
，重启planning算法，观察规划轨迹有何区别.
distance_approach_config {
weight_steer:0.3
weight_a:1.1
weight_steer_rate:3.0
weight_a_rate:2.5
weight_x:0.0//改为2.0
weight_y:0.0//改为2.0
weight_phi:0.0//改为2.0
weight_v:0.0
可以看到，轨迹更加贴近于混合Astar规划出来的轨迹。
planning.conf
中将
use_iterative_anchoring_smoother
设置为true,
enable_parallel_trajectory_smoothing
设置为true，采用DL-IAPS算法平滑，观察规划轨迹有何不同
--enable_smoother_failsafe
--enable_parallel_trajectory_smoothing=true--nouse_s_curve_speed_smooth
--use_iterative_anchoring_smoother=true
DL-IAPS算法直接将第一段平滑为直线。
5.2 靠边停车场景实践:
将
planning.conf
中的
enable_scenario_pull_over
由false改为true，打开靠边停车场景
地图选择San Mateo，重新打开Routing , planning,prediction,taskmanager模块，在scenario_set中选择靠边停车场景进行仿真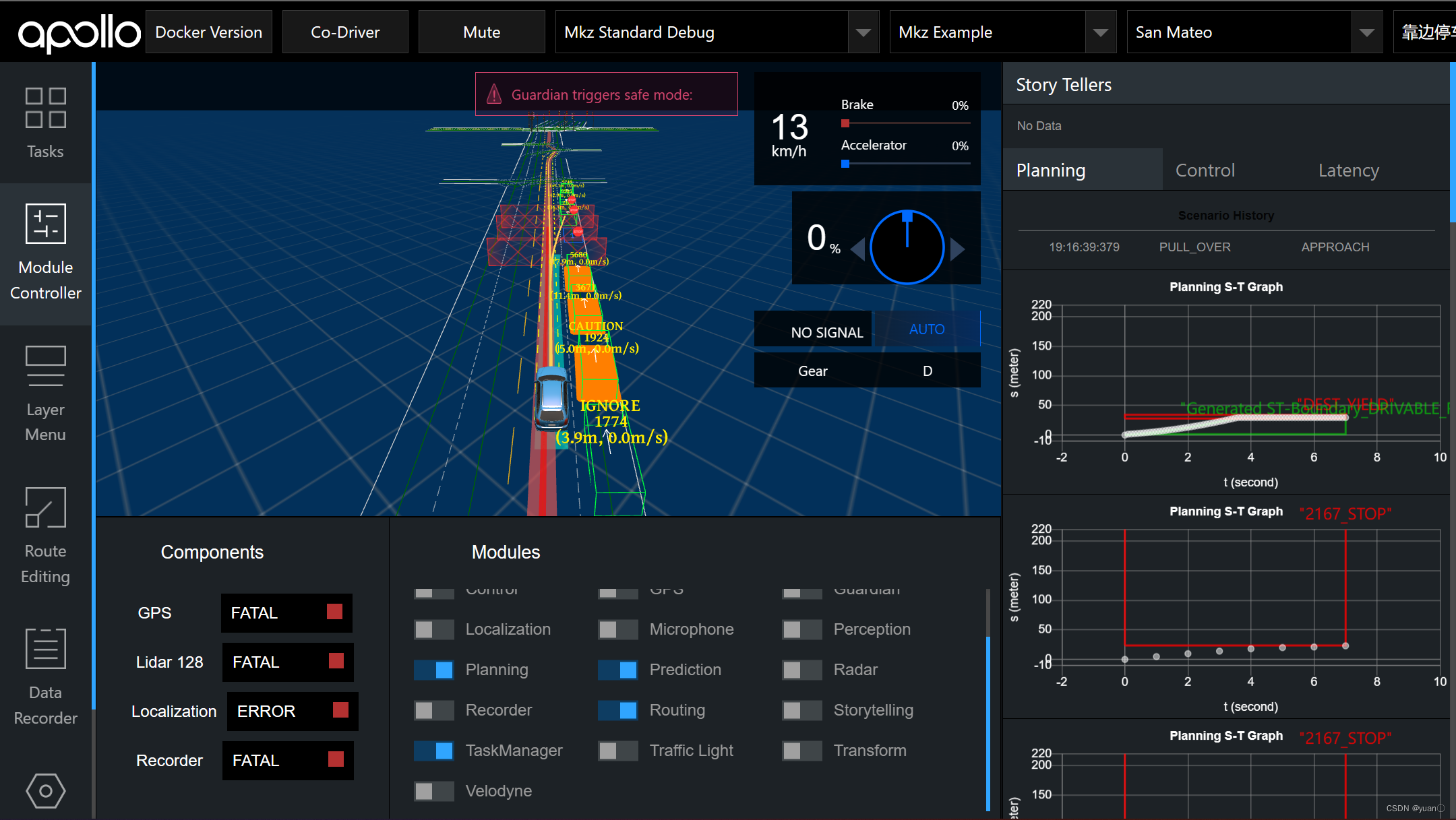
因为周围有障碍物，所以规划轨迹有所不同。
5.3 python脚本实验
打开notebook，输入以下指令。
%matplotlib notebook
run modules/tools/open_space_visualization/distance_approach_visualizer.py
垂直泊车运行
脚本代码
#!/usr/bin/env python3################################################################################ Copyright 2018 The Apollo Authors. All Rights Reserved.## Licensed under the Apache License, Version 2.0 (the "License");# you may not use this file except in compliance with the License.# You may obtain a copy of the License at## http://www.apache.org/licenses/LICENSE-2.0## Unless required by applicable law or agreed to in writing, software# distributed under the License is distributed on an "AS IS" BASIS,# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.# See the License for the specific language governing permissions and# limitations under the License.###############################################################################import math
import time
import sys
from matplotlib import animation
import matplotlib.patches as patches
import matplotlib.pyplot as plt
import numpy as np
from distance_approach_python_interface import*
result_file ="/tmp/open_space_osqp_ipopt.csv"# def SmoothTrajectory(visualize_flag):defSmoothTrajectory(visualize_flag, sx, sy, sphi):# initialze object
OpenSpacePlanner = DistancePlanner()# parameter(except max, min and car size is defined in proto)
num_output_buffer =10000#sphi = 0.0# 更改scenario，进行不同场景下的泊车
scenario ="backward"#scenario = "parallel"if scenario =="backward":
left_boundary_x =[-13.6407054776,0.0,0.0515703622475]
left_boundary_y =[0.0140634663703,0.0,-5.15258191624]
down_boundary_x =[0.0515703622475,2.8237895441]
down_boundary_y =[-5.15258191624,-5.15306980547]
right_boundary_x =[2.8237895441,2.7184833539,16.3592013995]
right_boundary_y =[-5.15306980547,-0.0398078878812,-0.011889513383]
up_boundary_x =[16.3591910364,-13.6406951857]
up_boundary_y =[5.60414234644,5.61797800844]if scenario =="parallel":
left_boundary_x =[-13.64,0.0,0.0]
left_boundary_y =[0.0,0.0,-2.82]
down_boundary_x =[0.0,9.15]
down_boundary_y =[-2.82,-2.82]
right_boundary_x =[9.15,9.15,16.35]
right_boundary_y =[-2.82,0.0,0.0]
up_boundary_x =[16.35,-13.64]
up_boundary_y =[5.60,5.60]
bound_x = left_boundary_x + down_boundary_x + right_boundary_x + up_boundary_x
bound_y = left_boundary_y + down_boundary_y + right_boundary_y + up_boundary_y
bound_vec =[]for i inrange(0,len(bound_x)):
bound_vec.append(bound_x[i])
bound_vec.append(bound_y[i])if scenario =="backward":# obstacles for distance approach(vertices coords in clock wise order)
ROI_distance_approach_parking_boundary =(
c_double *20)(*bound_vec)
OpenSpacePlanner.AddObstacle(
ROI_distance_approach_parking_boundary)# parking lot position
ex =1.359
ey =-3.86443643718
ephi =1.581
XYbounds =[min(bound_x),max(bound_x),min(bound_y),max(bound_y)]if scenario =="parallel":# obstacles for distance approach(vertices coords in clock wise order)
ROI_distance_approach_parking_boundary =(
c_double *20)(*bound_vec)
OpenSpacePlanner.AddObstacle(
ROI_distance_approach_parking_boundary)# parking lot position
ex =3.29
ey =-1.359
ephi =0
XYbounds =[min(bound_x),max(bound_x),min(bound_y),max(bound_y)]
x =(c_double * num_output_buffer)()
y =(c_double * num_output_buffer)()
phi =(c_double * num_output_buffer)()
v =(c_double * num_output_buffer)()
a =(c_double * num_output_buffer)()
steer =(c_double * num_output_buffer)()
opt_x =(c_double * num_output_buffer)()
opt_y =(c_double * num_output_buffer)()
opt_phi =(c_double * num_output_buffer)()
opt_v =(c_double * num_output_buffer)()
opt_a =(c_double * num_output_buffer)()
opt_steer =(c_double * num_output_buffer)()
opt_time =(c_double * num_output_buffer)()
opt_dual_l =(c_double * num_output_buffer)()
opt_dual_n =(c_double * num_output_buffer)()
size =(c_ushort *1)()
XYbounds_ctype =(c_double *4)(*XYbounds)
hybrid_time =(c_double *1)(0.0)
dual_time =(c_double *1)(0.0)
ipopt_time =(c_double *1)(0.0)
success =True
start = time.time()print("planning start")ifnot OpenSpacePlanner.DistancePlan(sx, sy, sphi, ex, ey, ephi, XYbounds_ctype):print("planning fail")
success =False# exit()
planning_time = time.time()- start
print("planning time is "+str(planning_time))
x_out =[]
y_out =[]
phi_out =[]
v_out =[]
a_out =[]
steer_out =[]
opt_x_out =[]
opt_y_out =[]
opt_phi_out =[]
opt_v_out =[]
opt_a_out =[]
opt_steer_out =[]
opt_time_out =[]
opt_dual_l_out =[]
opt_dual_n_out =[]if visualize_flag:# load result
OpenSpacePlanner.DistanceGetResult(x, y, phi, v, a, steer, opt_x,
opt_y, opt_phi, opt_v, opt_a, opt_steer, opt_time,
opt_dual_l, opt_dual_n, size,
hybrid_time, dual_time, ipopt_time)for i inrange(0, size[0]):
x_out.append(float(x[i]))
y_out.append(float(y[i]))
phi_out.append(float(phi[i]))
v_out.append(float(v[i]))
a_out.append(float(a[i]))
steer_out.append(float(steer[i]))
opt_x_out.append(float(opt_x[i]))
opt_y_out.append(float(opt_y[i]))
opt_phi_out.append(float(opt_phi[i]))
opt_v_out.append(float(opt_v[i]))
opt_a_out.append(float(opt_a[i]))
opt_steer_out.append(float(opt_steer[i]))
opt_time_out.append(float(opt_time[i]))for i inrange(0, size[0]*6):
opt_dual_l_out.append(float(opt_dual_l[i]))for i inrange(0, size[0]*16):
opt_dual_n_out.append(float(opt_dual_n[i]))# trajectories plot
fig1 = plt.figure(1, figsize =[9,6])
ax = fig1.add_subplot(111)for i inrange(0, size[0]):# warm start
downx =1.055* math.cos(phi_out[i]- math.pi /2)
downy =1.055* math.sin(phi_out[i]- math.pi /2)
leftx =1.043* math.cos(phi_out[i]- math.pi)
lefty =1.043* math.sin(phi_out[i]- math.pi)
x_shift_leftbottom = x_out[i]+ downx + leftx
y_shift_leftbottom = y_out[i]+ downy + lefty
warm_start_car = patches.Rectangle((x_shift_leftbottom, y_shift_leftbottom),3.89+1.043,1.055*2,
angle=phi_out[i]*180/ math.pi, linewidth=1, edgecolor='r', facecolor='none')#ax.add_patch(warm_start_car)
warm_start_arrow = patches.Arrow(
x_out[i], y_out[i],0.25* math.cos(phi_out[i]),0.25* math.sin(phi_out[i]),0.2, edgecolor='r',)#ax.add_patch(warm_start_arrow)# distance approach
downx =1.055* math.cos(opt_phi_out[i]- math.pi /2)
downy =1.055* math.sin(opt_phi_out[i]- math.pi /2)
leftx =1.043* math.cos(opt_phi_out[i]- math.pi)
lefty =1.043* math.sin(opt_phi_out[i]- math.pi)
x_shift_leftbottom = opt_x_out[i]+ downx + leftx
y_shift_leftbottom = opt_y_out[i]+ downy + lefty
smoothing_car = patches.Rectangle((x_shift_leftbottom, y_shift_leftbottom),3.89+1.043,1.055*2,
angle=opt_phi_out[i]*180/ math.pi, linewidth=1, edgecolor='y', facecolor='none')
smoothing_arrow = patches.Arrow(
opt_x_out[i], opt_y_out[i],0.25* math.cos(opt_phi_out[i]),0.25* math.sin(opt_phi_out[i]),0.2, edgecolor='y',)
ax.plot(x_out, y_out,"r")
ax.plot(opt_x_out, opt_y_out,"y")
ax.add_patch(smoothing_car)# ax.add_patch(smoothing_arrow)
ax.plot(sx, sy,"s")
ax.plot(ex, ey,"s")
ax.plot(left_boundary_x, left_boundary_y,"k")
ax.plot(down_boundary_x, down_boundary_y,"k")
ax.plot(right_boundary_x, right_boundary_y,"k")
ax.plot(up_boundary_x, up_boundary_y,"k")
plt.axis('equal')# input plot
fig2 = plt.figure(2, figsize =[9,6])
v_graph = fig2.add_subplot(411)
v_graph.title.set_text('v')
v_graph.plot(np.linspace(0, size[0], size[0]), v_out)
v_graph.plot(np.linspace(0, size[0], size[0]), opt_v_out)
a_graph = fig2.add_subplot(412)
a_graph.title.set_text('a')
a_graph.plot(np.linspace(0, size[0], size[0]), a_out)
a_graph.plot(np.linspace(0, size[0], size[0]), opt_a_out)
steer_graph = fig2.add_subplot(413)
steer_graph.title.set_text('steering')
steer_graph.plot(np.linspace(0, size[0], size[0]), steer_out)
steer_graph.plot(np.linspace(0, size[0], size[0]), opt_steer_out)
steer_graph = fig2.add_subplot(414)
steer_graph.title.set_text('phi')
steer_graph.plot(np.linspace(0, size[0], size[0]), opt_phi_out)# dual variables
fig3 = plt.figure(3, figsize =[9,6])
dual_l_graph = fig3.add_subplot(211)
dual_l_graph.title.set_text('dual_l')
dual_l_graph.plot(np.linspace(0, size[0]*6, size[0]*6), opt_dual_l_out)
dual_n_graph = fig3.add_subplot(212)
dual_n_graph.title.set_text('dual_n')
dual_n_graph.plot(np.linspace(0, size[0]*16, size[0]*16), opt_dual_n_out)
plt.show()returnTrueifnot visualize_flag:if success:# load result
OpenSpacePlanner.DistanceGetResult(x, y, phi, v, a, steer, opt_x,
opt_y, opt_phi, opt_v, opt_a, opt_steer, opt_time,
opt_dual_l, opt_dual_n, size,
hybrid_time, dual_time, ipopt_time)for i inrange(0, size[0]):
x_out.append(float(x[i]))
y_out.append(float(y[i]))
phi_out.append(float(phi[i]))
v_out.append(float(v[i]))
a_out.append(float(a[i]))
steer_out.append(float(steer[i]))
opt_x_out.append(float(opt_x[i]))
opt_y_out.append(float(opt_y[i]))
opt_phi_out.append(float(opt_phi[i]))
opt_v_out.append(float(opt_v[i]))
opt_a_out.append(float(opt_a[i]))
opt_steer_out.append(float(opt_steer[i]))
opt_time_out.append(float(opt_time[i]))# check end_pose distacne
end_pose_dist = math.sqrt((opt_x_out[-1]- ex)**2+(opt_y_out[-1]- ey)**2)
end_pose_heading =abs(opt_phi_out[-1]- ephi)
reach_end_pose =(end_pose_dist <=0.1and end_pose_heading <=0.17)else:
end_pose_dist =100.0
end_pose_heading =100.0
reach_end_pose =0return[success, end_pose_dist, end_pose_heading, reach_end_pose, opt_x_out, opt_y_out, opt_phi_out, opt_v_out, opt_a_out, opt_steer_out, opt_time_out,
hybrid_time, dual_time, ipopt_time, planning_time]returnFalseif __name__ =='__main__':
visualize_flag =True
sx =0.0
sy =3
sphi =0.0
SmoothTrajectory(visualize_flag, sx, sy, sphi)
sys.exit()
visualize_flag =False
planning_time_stats =[]
hybrid_time_stats =[]
dual_time_stats =[]
ipopt_time_stats =[]
end_pose_dist_stats =[]
end_pose_heading_stats =[]
test_count =0
success_count =0for sx in np.arange(-10,10,1.0):for sy in np.arange(2,4,0.5):print("sx is "+str(sx)+" and sy is "+str(sy))
test_count +=1
result = SmoothTrajectory(visualize_flag, sx, sy, sphi)# if result[0] and result[3]: # success cases onlyif result[0]:
success_count +=1
planning_time_stats.append(result[-1])
ipopt_time_stats.append(result[-2][0])
dual_time_stats.append(result[-3][0])
hybrid_time_stats.append(result[-4][0])
end_pose_dist_stats.append(result[1])
end_pose_heading_stats.append(result[2])print("success rate is "+str(float(success_count)/float(test_count)))print("min is "+str(min(planning_time_stats)))print("max is "+str(max(planning_time_stats)))print("average is "+str(sum(planning_time_stats)/len(planning_time_stats)))print("max end_pose_dist difference is: "+str(max(end_pose_dist_stats)))print("min end_pose_dist difference is: "+str(min(end_pose_dist_stats)))print("average end_pose_dist difference is: "+str(sum(end_pose_dist_stats)/len(end_pose_dist_stats)))print("max end_pose_heading difference is: "+str(max(end_pose_heading_stats)))print("min end_pose_heading difference is: "+str(min(end_pose_heading_stats)))print("average end_pose_heading difference is: "+str(sum(end_pose_heading_stats)/len(end_pose_heading_stats)))
module_timing = np.asarray([hybrid_time_stats, dual_time_stats, ipopt_time_stats])
np.savetxt(result_file, module_timing, delimiter=",")print("average hybrid time(s): %4.4f, with max: %4.4f, min: %4.4f"%(sum(hybrid_time_stats)/len(hybrid_time_stats)/1000.0,max(hybrid_time_stats)/1000.0,min(hybrid_time_stats)/1000.0))print("average dual time(s): %4.4f, with max: %4.4f, min: %4.4f"%(sum(dual_time_stats)/len(dual_time_stats)/1000.0,max(dual_time_stats)/1000.0,min(dual_time_stats)/1000.0))print("average ipopt time(s): %4.4f, with max: %4.4f, min: %4.4f"%(sum(ipopt_time_stats)/len(ipopt_time_stats)/1000.0,max(ipopt_time_stats)/1000.0,min(ipopt_time_stats)/1000.0))
平行泊车运行（失败了，脚本还存在着一些问题）
本文转载自: https://blog.csdn.net/sinat_52032317/article/details/128564014
版权归原作者 yuan〇 所有， 如有侵权，请联系我们删除。
版权归原作者 yuan〇 所有， 如有侵权，请联系我们删除。