使用Pytorch Geometric 进行链接预测代码示例

PyTorch Geometric (PyG)是构建图神经网络模型和实验各种图卷积的主要工具。在本文中我们将通过链接预测来对其进行介绍。

链接预测答了一个问题:哪两个节点应该相互链接?我们将通过执行“转换分割”，为建模准备数据。为批处理准备专用的图数据加载器。在Torch Geometric中构建一个模型，使用PyTorch Lightning进行训练，并检查模型的性能。

库准备

Torch 这个就不用多介绍了

Torch Geometric 图形神经网络的主要库，也是本文介绍的重点

PyTorch Lightning 用于训练、调优和验证模型。它简化了训练的操作

Sklearn Metrics和Torchmetrics 用于检查模型的性能。

PyTorch Geometric有一些特定的依赖关系，如果你安装有问题，请参阅其官方文档。

数据准备

我们将使用Cora ML引文数据集。数据集可以通过Torch Geometric访问。

 data = tg.datasets.CitationFull(root="data", name="Cora_ML")

默认情况下，Torch Geometric数据集可以返回多个图形。我们看看单个图是什么样子的

 data[0]
 > Data(x=[2995, 2879], edge_index=[2, 16316], y=[2995])

这里的 X是节点的特征。edge_index是2 x (n条边)矩阵(第一维= 2，被解释为:第0行-源节点/“发送方”，第1行-目标节点/“接收方”)。

链接拆分

我们将从拆分数据集中的链接开始。使用20%的图链接作为验证集，10%作为测试集。这里不会向训练数据集中添加负样本，因为这样的负链接将由批处理数据加载器实时创建。

一般来说，负采样会创建“假”样本(在我们的例子中是节点之间的链接)，因此模型学习如何区分真实和虚假的链接。负抽样基于抽样的理论和数学，具有一些很好的统计性质。

首先:让我们创建一个链接拆分对象。

 link_splitter = tg.transforms.RandomLinkSplit(
     num_val=0.2, 
     num_test=0.1, 
     add_negative_train_samples=False,
     disjoint_train_ratio=0.8)

disjoint_train_ratio调节在“监督”阶段将使用多少条边作为训练信息。剩余的边将用于消息传递(网络中的信息传输阶段)。

图神经网络中至少有两种分割边的方法:归纳分割和传导分割。转换方法假设GNN需要从图结构中学习结构模式。在归纳设置中，可以使用节点/边缘标签进行学习。本文最后有两篇论文详细讨论了这些概念，并进行了额外的形式化:([1]，[3])。

 train_g, val_g, test_g = link_splitter(data[0])
 
 > Data(x=[2995, 2879], edge_index=[2, 2285], y=[2995], edge_label=[9137], edge_label_index=[2, 9137])

在这个操作之后，我们有了一些新的属性:

edge_label ：描述边缘是否为真/假。这是我们想要预测的。

edge_label_index 是一个2 x NUM EDGES矩阵，用于存储节点链接。

让我们看看样本的分布

 th.unique(train_g.edge_label, return_counts=True)
 > (tensor([1.]), tensor([9137]))
 
 th.unique(val_g.edge_label, return_counts=True)
 > (tensor([0., 1.]), tensor([3263, 3263]))
 
 th.unique(val_g.edge_label, return_counts=True)
 > (tensor([0., 1.]), tensor([3263, 3263]))

对于训练数据没有负边(我们将训练时创建它们)，对于val/测试集——已经以50:50的比例有了一些“假”链接。

模型

现在我们可以在使用GNN进行模型的构建了一个

 class GNN(nn.Module):
     
     def __init__(
         self, 
         dim_in: int, 
         conv_sizes: Tuple[int, ...], 
         act_f: nn.Module = th.relu, 
         dropout: float = 0.1,
         *args, 
         **kwargs):
         super().__init__()
         self.dim_in = dim_in
         self.dim_out = conv_sizes[-1]
         self.dropout = dropout
         self.act_f = act_f
         last_in = dim_in
         layers = []
         
         # Here we build subsequent graph convolutions.
         for conv_sz in conv_sizes:
             # Single graph convolution layer
             conv = tgnn.SAGEConv(in_channels=last_in, out_channels=conv_sz, *args, **kwargs)
             last_in = conv_sz
             layers.append(conv)
         self.layers = nn.ModuleList(layers)
     
     def forward(self, x: th.Tensor, edge_index: th.Tensor) -> th.Tensor:
         h = x
         # For every graph convolution in the network...
         for conv in self.layers:
             # ... perform node embedding via message passing
             h = conv(h, edge_index)
             h = self.act_f(h)
             if self.dropout:
                 h = nn.functional.dropout(h, p=self.dropout, training=self.training)
         return h

这个模型中值得注意的部分是一组图卷积——在我们的例子中是SAGEConv。SAGE卷积的正式定义为:

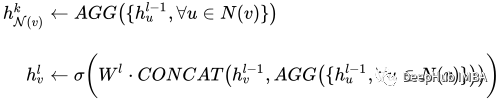
v是当前节点，节点v的N(v)个邻居。要了解更多关于这种卷积类型的信息，请查看GraphSAGE[1]的原始论文

让我们检查一下模型是否可以使用准备好的数据进行预测。这里PyG模型的输入是节点特征X的矩阵和定义edge_index的链接。

 gnn = GNN(train_g.x.size()[1], conv_sizes=[512, 256, 128])
 with th.no_grad():
     out = gnn(train_g.x, train_g.edge_index)
     
 out
 
 
 > tensor([[0.0000, 0.0000, 0.0051,  ..., 0.0997, 0.0000, 0.0000],
         [0.0107, 0.0000, 0.0576,  ..., 0.0651, 0.0000, 0.0000],
         [0.0000, 0.0000, 0.0102,  ..., 0.0973, 0.0000, 0.0000],
         ...,
         [0.0000, 0.0000, 0.0549,  ..., 0.0671, 0.0000, 0.0000],
         [0.0000, 0.0000, 0.0166,  ..., 0.0000, 0.0000, 0.0000],
         [0.0000, 0.0000, 0.0034,  ..., 0.1111, 0.0000, 0.0000]])

我们模型的输出是一个维度为:N个节点x嵌入大小的节点嵌入矩阵。

PyTorch Lightning

PyTorch Lightning主要用作训练，但是这里我们在GNN的输出后面增加了一个Linear层做为预测是否链接的输出头。

 class LinkPredModel(pl.LightningModule):
     
     def __init__(
         self,
         dim_in: int,
         conv_sizes: Tuple[int, ...], 
         act_f: nn.Module = th.relu, 
         dropout: float = 0.1,
         lr: float = 0.01,
         *args, **kwargs):
         super().__init__()
         
         # Our inner GNN model
         self.gnn = GNN(dim_in, conv_sizes=conv_sizes, act_f=act_f, dropout=dropout)
         
         # Final prediction model on links.
         self.lin_pred = nn.Linear(self.gnn.dim_out, 1)
         self.lr = lr
     
     def forward(self, x: th.Tensor, edge_index: th.Tensor) -> th.Tensor:
         # Step 1: make node embeddings using GNN.
         h = self.gnn(x, edge_index)
         
         # Take source nodes embeddings- senders
         h_src = h[edge_index[0, :]]
         # Take target node embeddings - receivers
         h_dst = h[edge_index[1, :]]
         
         # Calculate the product between them
         src_dst_mult = h_src * h_dst
         # Apply non-linearity
         out = self.lin_pred(src_dst_mult)
         return out
     
     def _step(self, batch: th.Tensor, phase: str='train') -> th.Tensor:
         yhat_edge = self(batch.x, batch.edge_label_index).squeeze()
         y = batch.edge_label
         loss = nn.functional.binary_cross_entropy_with_logits(input=yhat_edge, target=y)
         f1 = tm.functional.f1_score(preds=yhat_edge, target=y, task='binary')
         prec = tm.functional.precision(preds=yhat_edge, target=y, task='binary')
         recall = tm.functional.recall(preds=yhat_edge, target=y, task='binary')
         
         # Watch for logging here - we need to provide batch_size, as (at the time of this implementation)
         # PL cannot understand the batch size.
         self.log(f"{phase}_f1", f1, batch_size=batch.edge_label_index.shape[1])
         self.log(f"{phase}_loss", loss, batch_size=batch.edge_label_index.shape[1])
         self.log(f"{phase}_precision", prec, batch_size=batch.edge_label_index.shape[1])
         self.log(f"{phase}_recall", recall, batch_size=batch.edge_label_index.shape[1])
 
         return loss
     
     def training_step(self, batch, batch_idx):
         return self._step(batch)
     
     def validation_step(self, batch, batch_idx):
         return self._step(batch, "val")
     
     def test_step(self, batch, batch_idx):
         return self._step(batch, "test")
     
     def predict_step(self, batch):
         x, edge_index = batch
         return self(x, edge_index)
     
     def configure_optimizers(self):
         return th.optim.Adam(self.parameters(), lr=self.lr)

PyTorch Lightning的作用是帮我们简化了训练的步骤，我们只需要配置一些函数即可，我们可以使用以下命令测试模型是否可用

 model = LinkPredModel(val_g.x.size()[1], conv_sizes=[512, 256, 128])
 with th.no_grad():
     out = model.predict_step((val_g.x, val_g.edge_label_index))

训练

对于训练的步骤，需要特殊处理的是数据加载器。

图数据需要特殊处理——尤其是链接预测。PyG有一些专门的数据加载器类，它们负责正确地生成批处理。我们将使用:tg.loader.LinkNeighborLoader，它接受以下输入:

要批量加载的数据(图)。num_neighbors 每个节点在一次“跳”期间加载的最大邻居数量。指定邻居数目的列表1 - 2 - 3 -…-K。对于非常大的图形特别有用。

edge_label_index 哪个属性已经指示了真/假链接。

neg_sampling_ratio -负样本与真实样本的比例。

 train_loader = tg.loader.LinkNeighborLoader(
     train_g,
     num_neighbors=[-1, 10, 5],
     batch_size=128,
     edge_label_index=train_g.edge_label_index,
     
     # "on the fly" negative sampling creation for batch
     neg_sampling_ratio=0.5
 )
 
 val_loader = tg.loader.LinkNeighborLoader(
     val_g,
     num_neighbors=[-1, 10, 5],
     batch_size=128,
     edge_label_index=val_g.edge_label_index,
     edge_label=val_g.edge_label,
 
     # negative samples for val set are done already as ground-truth
     neg_sampling_ratio=0.0
 )
 
 test_loader = tg.loader.LinkNeighborLoader(
     test_g,
     num_neighbors=[-1, 10, 5],
     batch_size=128,
     edge_label_index=test_g.edge_label_index,
     edge_label=test_g.edge_label,
     
     # negative samples for test set are done already as ground-truth
     neg_sampling_ratio=0.0
 )

下面就是训练模型

 model = LinkPredModel(val_g.x.size()[1], conv_sizes=[512, 256, 128])
 trainer = pl.Trainer(max_epochs=20, log_every_n_steps=5)
 
 # Validate before training - we will see results of untrained model.
 trainer.validate(model, val_loader)
 
 # Train the model
 trainer.fit(model=model, train_dataloaders=train_loader, val_dataloaders=val_loader)

试验数据核对，查看分类报告和ROC曲线。

 with th.no_grad():
     yhat_test_proba = th.sigmoid(model(test_g.x, test_g.edge_label_index)).squeeze()
     yhat_test_cls = yhat_test_proba >= 0.5
     
 print(classification_report(y_true=test_g.edge_label, y_pred=yhat_test_cls))

结果看起来还不错:

               precision    recall  f1-score   support
 
          0.0       0.68      0.70      0.69      1631
          1.0       0.69      0.66      0.68      1631
 
     accuracy                           0.68      3262
    macro avg       0.68      0.68      0.68      3262
 weighted avg       0.68      0.68      0.68      3262

ROC曲线也不错

我们训练的模型并不特别复杂，也没有经过精心调整，但它完成了工作。当然这只是一个为了演示使用的小型数据集。

总结

图神经网络尽管看起来很复杂，但是PyTorch Geometric为我们提供了一个很好的解决方案。我们可以直接使用其中内置的模型实现，这方便了我们使用和简化了入门的门槛。

本文代码：

https://github.com/maddataanalyst/blogposts_code/blob/main/graph_nns_series/pyg_pyl_perfect_match/pytorch-geometric-lightning-perfect-match.ipynb

参考：

Hamilton, W., Ying, Z., & Leskovec, J. (2017). Inductive representation learning on large graphs. Advances in neural information processing systems, 30.
McCormick, C. (2017). Word2Vec Tutorial Part 2 — Negative Sampling.
Rossi, A., Tiezzi, M., Dimitri, G. M., Bianchini, M., Maggini, M., & Scarselli, F. (2018). Inductive–transductive learning with graph neural networks. In Artificial Neural Networks in Pattern Recognition: 8th IAPR TC3 Workshop, ANNPR 2018, Siena, Italy, September 19–21, 2018, Proceedings 8 (pp. 201–212). Springer International Publishing.

作者：Filip Wójcik

标签：深度学习图神经网络 Pytorch

使用Pytorch Geometric 进行链接预测代码示例

库准备

数据准备

模型

PyTorch Lightning

训练

总结

发表评论

“使用Pytorch Geometric 进行链接预测代码示例”的评论:

关于作者

Deephub

相关阅读

文章导航