Unit Scaling 是一种新的低精度机器学习方法,能够在没有损失缩放的情况下训练 FP16 和 FP8 中的语言模型。
使用FP16和BFLOAT16替代FP32可以将内存、带宽和计算需求的大幅减少,这也是目前越来越大的模型所需要的。
背景介绍
随着支持fp8的硬件的发展,在不影响效率的前提下,进一步降低精度也成为了可能。但是这些较小的、低精度的格式在实践中并不总是易于使用。对于FP8来说则更加困难。因为这些较小的格式通常将用户限制在更窄的可表示值范围内。为了解决这个问题,Graphcore Research开发了一种新方法,我们称之为Unit Scaling。
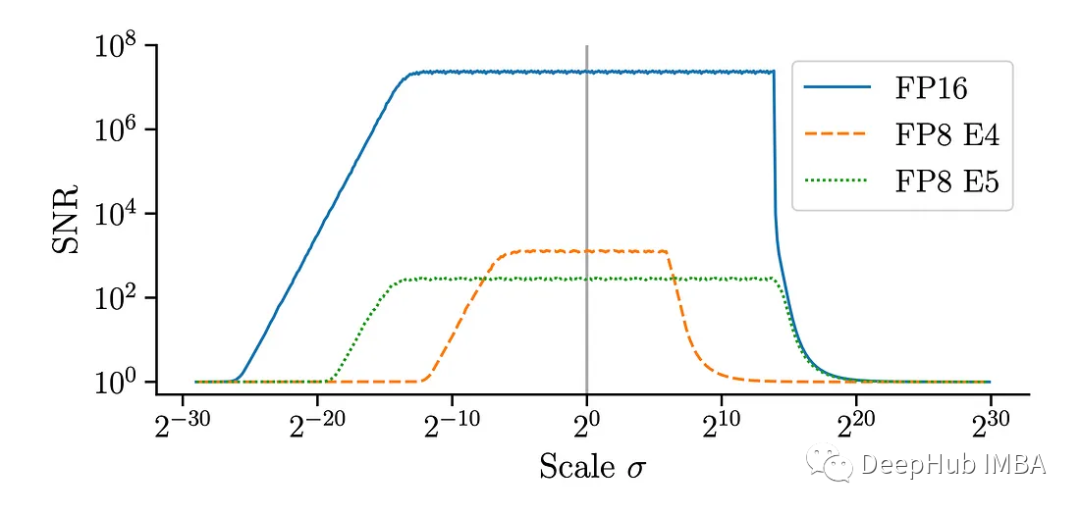
上图为FP16和FP8中量化的不同尺度的正态分布的信噪比(SNR)。对于较小的数字格式,信号在较窄的尺度范围内较强。
Unit Scaling是一种模型设计技术,它在初始化时根据缩放原则进行操作:也就是说对激活、权重和梯度的单位方差进行缩放。模型会自动生成针对低精度数字格式进行良好缩放的张量。并且使用更简单,并最大限度地减少这些表示的缺点,与低精度训练的替代方法不同,它引入的开销和额外的复杂性很小。
论文的方法取得了突破性的成果:首次在 FP16 甚至 FP8 中准确地训练了 BERT Base 和 BERT Large 模型,并且没有缩放的性能损失。模型也不需要额外的超参数,可以直接使用。
对于关心结果并因此希望在 FP16 和 FP8 中进行训练的人来说,Unit Scaling提供了一个直接的解决方案。
FP16/FP8训练的现有方法
FP16和FP8训练需要某种形式的缩放来保持值在范围内。目前的做法如下:
1、(静态)损失缩放
缩小范围对于训练期间的向反向传播是具有挑战性的通常会导致梯度下溢。为了解决这个问题,最常见的方法是将损失乘以超参数以增加梯度的大小 [1]。由于没有原则性的方法来提前选择损失的规模,所以这个超参数通常需要多次运行。
2、自动损失缩放
通过基于运行时的梯度溢出(或直方图)[2] 动态调整损失比例,可以避免超参数扫描的需要。但是这种自动方案会增加开销和复杂性。
3、张量缩放
上述方法的另一个缺点是它们只提供单一的全局损失尺度。另外一种解决方案是根据张量统计 [3] 重新缩放值。这也是一种自动/运行时方案,很复杂且难以有效实施。

Unit Scaling
Unit Scaling 在前向和反向传播中引入局部缩放因子控制值的范围。选择的范围是基于每个操作符如何影响值规模的理解,而并不是使用运行时分析得到的。通过选择正确的比例因子,每个操作都大致保持其输入的比例。通过将其应用于所有操作,可以控制整个模型中传播初始(单位)比例,从而实现全局的缩放。
这种方法比自动缩放方案更简单,因为唯一的额外开销是应用缩放因子。对于 BERT Large,这会将 FLOPs 增加 0.2%,应该可以忽略不计。
模型可以通过应用以下方法进行Unit Scaling:
- 用单位方差初始化无偏差参数
- 计算所有操作的理想比例因子
- 识别非切边并限制使用它们的操作具有相同的缩放比例
- 用加权的加法替换加法
下面我们将更详细地解释这些规则。
1、理想的比例因子
我们可以对一些操作进行数学分析,以确定它们如何影响输入的方差。
比如基本矩阵乘法 XW(其中 X 是 (b × m) 矩阵,W 是 (m × n) 矩阵)的输出方差为 σ(X)² · σ(W)² · m。要缩放此操作,我们必须确保 σ(X)² = σ(W)² = 1,然后将 1/√m 乘法添加到输出。
对于反向传播,需要引入了两个新的矩阵乘法,理想的比例因子为 1/√n 和 1/√b。其他操作也可以类似分析,输出方差不容易分析,所以可以使用经验方法来找到缩放因子。
在论文作者中提供了更详细的分析,以及常见操作的概要及其理想的比例因子。
2、切边
直接将这些理想的比例因子应用于正向和反向传播中会产生无效的梯度。为了避免这种情况,某些操作需要使用共享的缩放因子。
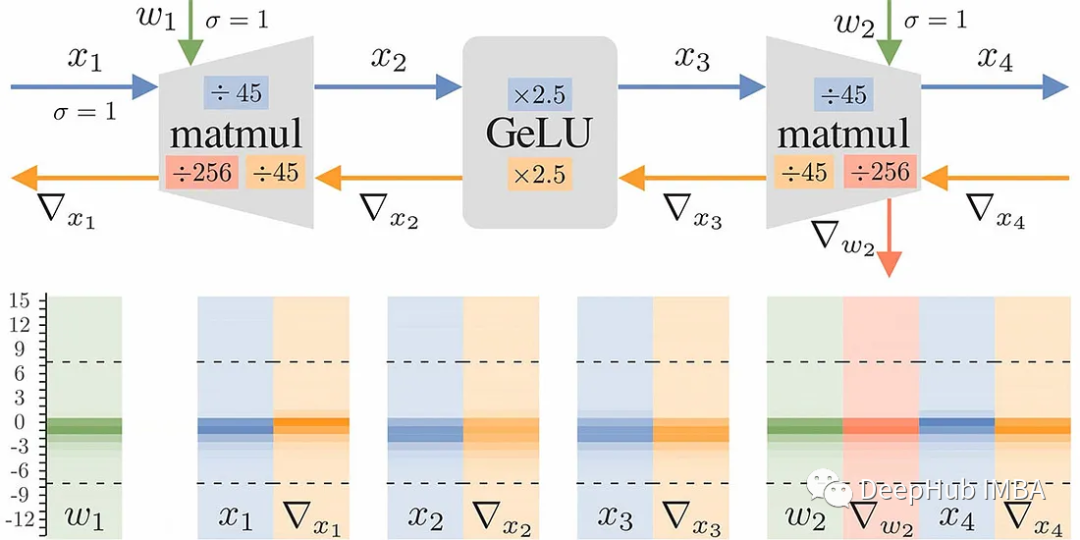
我们使用前向计算图并找到所有没有用切边表示的变量(如果去掉这些边,会将图分割成两个不相连的更小的图)。比如,下面是一个transformer的FFN层:
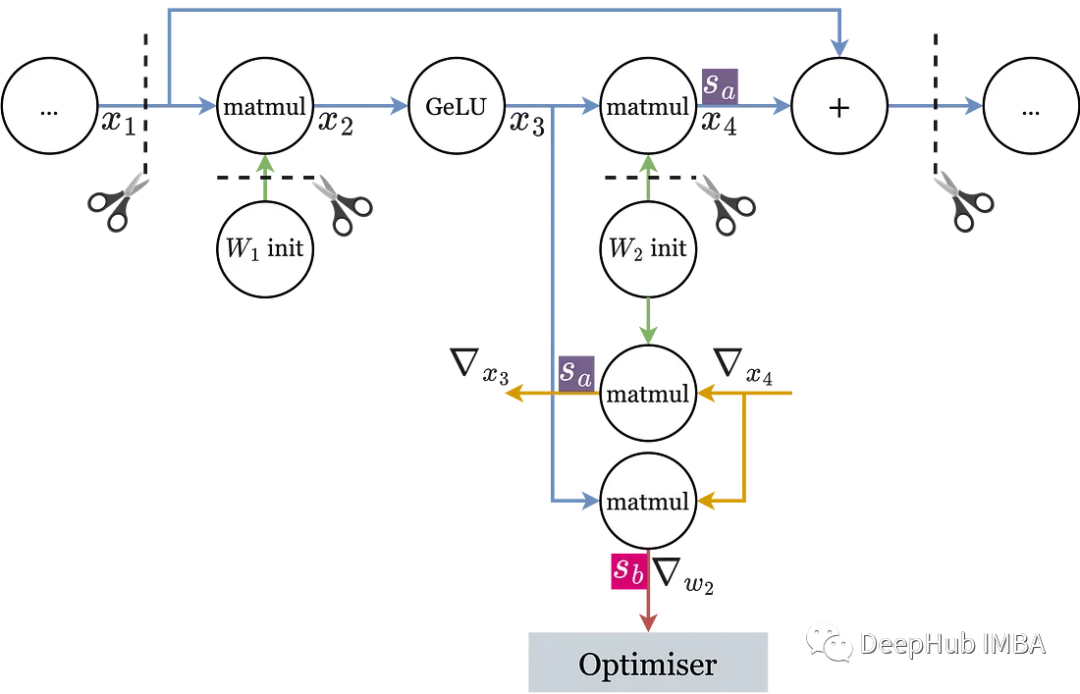
在权重、输入和输出变量上有切边。该图还显示了为第二个matmul的反向传播生成的梯度操作(我们只考虑正向图的切边)。
因为 x₃ 不是切边,所以可以限制 ∇x₃ 的 matmul 使用与前向传播中相同的比例因子,但是由于 w2 是切边,它允许有自己的反向缩放因子,所以为受约束的操作选择共享比例因子,采用之前计算的理想比例因子的几何平均值。
这个规则听起来很复杂,但实际上它通常可以归结为一个简单的过程:为权重梯度提供它们自己的比例因子(也就是模型中的任何编码器/解码器层)。
3、加权加法操作
最后一步是用加权的加法替换加法操作。根据设计的单位缩放产生的变量具有相等的尺度,如果我们将两个张量相加,它们实际上都具有相等的权重。但是在某些情况下,例如残差连接就需要一个不平衡的权重来获得良好的性能。所以将加法操作替换为加权(和单位缩放)加法等效操作。
对于残差连接,可以推导出以下方案:
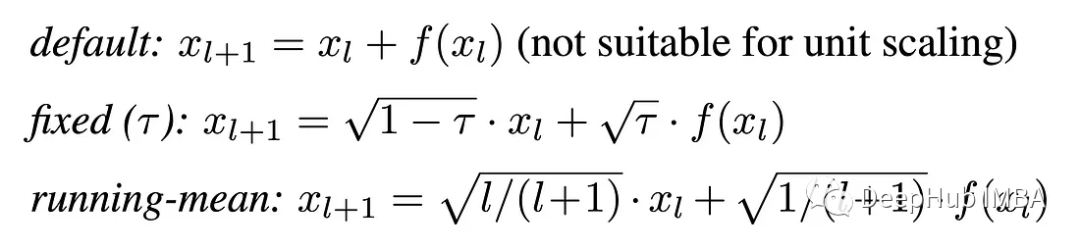
代码实现
下面的代码展示了一个在PyTorch中实现Unit Scaling的FFN层。
首先定义创建基本操作的缩放版本,例如scaled_projection:
classScaledGrad(autograd.Function):
@staticmethod
defforward(ctx, X, alpha, beta):
ctx.save_for_backward(tensor(beta, dtype=X.dtype))
returnalpha*X
@staticmethod
defbackward(ctx, grad_Y):
beta, =ctx.saved_tensors
returnbeta*grad_Y, None, None
defscaled(X, alpha=1, beta=1):
"""forward: Y = X * alpha, backward: grad_X = grad_Y * beta"""
returnScaledGrad.apply(X, alpha, beta)
defscaled_projection(X, W):
(b, _), (m, n) =X.shape, W.shape
alpha=beta_X= (m*n) **-(1/4) beta_W=b**-(1/2)
X=scaled(X, beta=beta_X)
W=scaled(W, beta=beta_W)
returnscaled(matmul(X, W), alpha)
这样我们就可以创建完整的层。我们只演示一个标准FFN和它的缩放版本:
classFFN(nn.Module):
def__init__(self, d, h):
super().__init__()
self.norm=LayerNorm(d)
sigma= (d*h) **-(1/4)
self.W_1=Parameter(randn(d, h) *sigma)
self.W_2=Parameter(randn(h, d) *sigma)
defforward(self, X):
Z=self.norm(X)
Z=matmul(Z, self.W_1) Z=gelu(Z)
Z=matmul(Z, self.W_2) returnX+Z
classScaledFFN(nn.Module):
def__init__(self, d, h, tau):
super().__init__()
self.norm=ScaledLayerNorm(d) # Not defined here
self.W1=Parameter(randn(d, h))
self.W2=Parameter(randn(h, d))
self.tau=tau
defforward(self, X):
a= (1-self.tau) ** (1/2)
b=self.tau** (1/2)
Z=self.norm(scaled(X, beta=b))
Z=scaled_projection(Z, self.W1)
Z=scaled_gelu(Z) # Not defined here
Z=scaled_projection(Z, self.W2)
returnX*a+scaled(Z, b) # fixed(𝜏) weighted add
结果展示
实验结果表明,这个方法在广泛的模型中是有效的,并且可以开箱即用,不需要额外的超参数调优。
1、小规模的实验
第一组实验验证了在不同模型架构上的广泛适用性。在FP32和FP16中训练了大量具有和不具有Unit Scaling的小型字符级语言模型,并比较了结果。
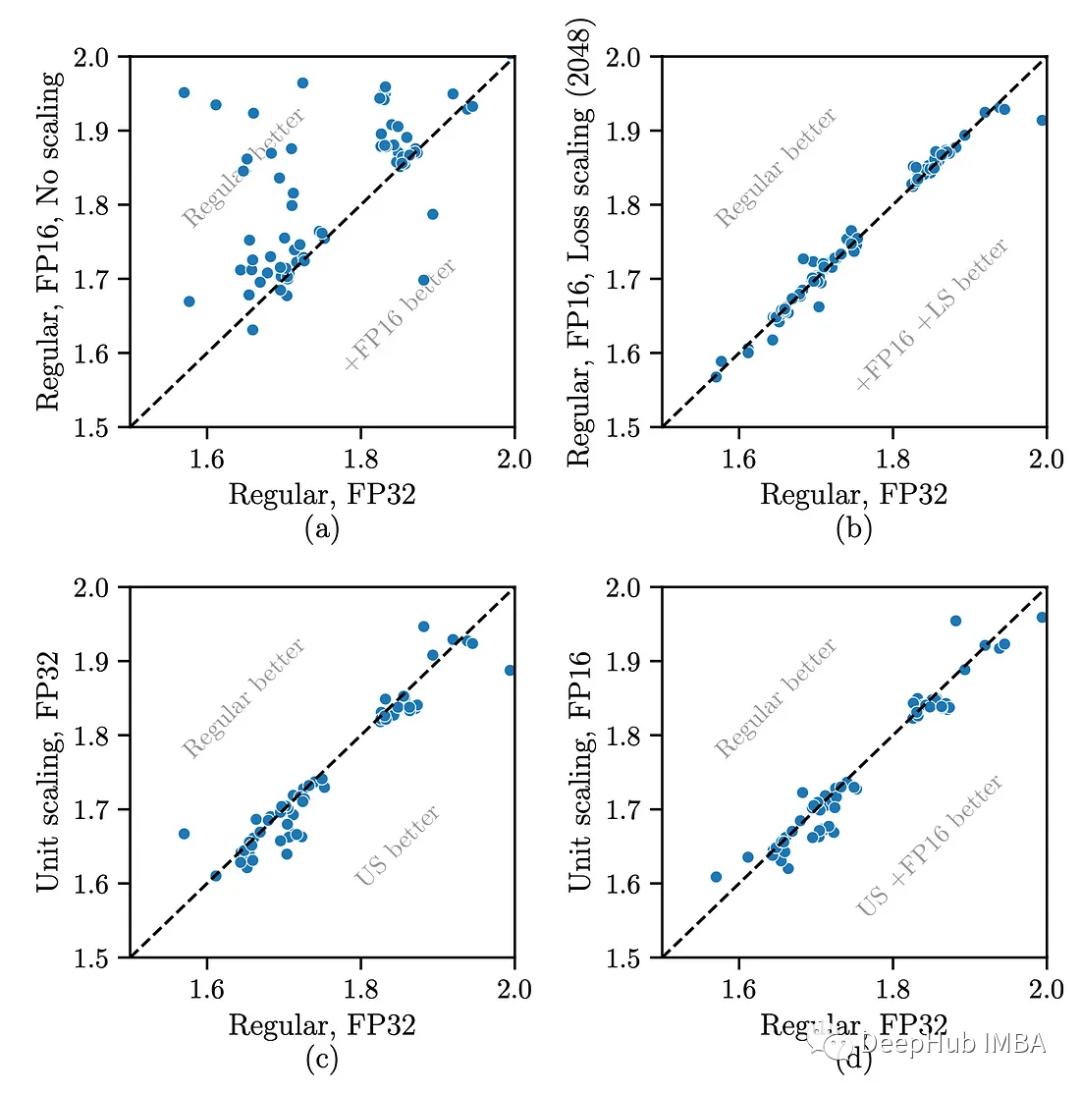
在几乎所有情况下,它都与基线性能匹配,甚至略有提高。当从FP32切换到FP16时,不需要调优。
2、大规模的实验
第二组实验在一个更大、更现实的生产级模型BERT[4]上验证了有效性。对单Unit Scaling模型进行调整,使其与标准BERT实现保持一致,然后使用来自英文维基百科文章的文本对其进行训练。
我们对SQuAD v1.0和SQuAD v2.0评估任务的结果如下:
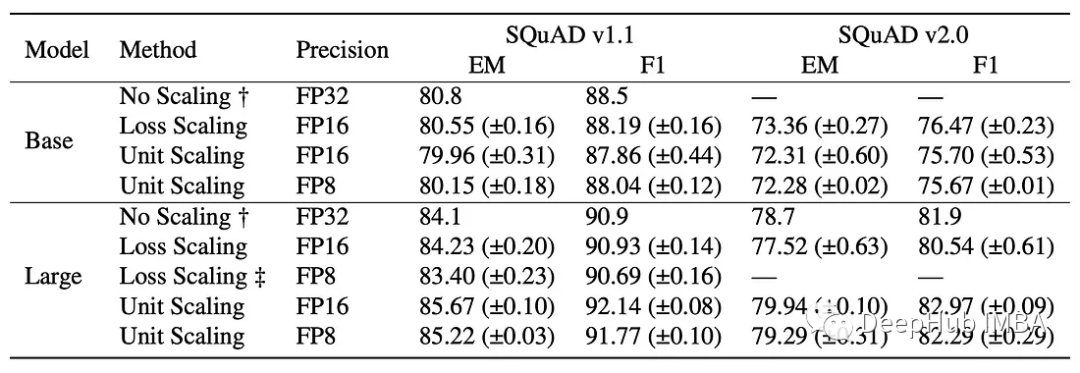
Unit Scaling能够获得与标准(基线)模型相同的性能,并且在所有情况下都可以直接使用。基线模型和Unit Scaling模型并不完全相同,但是它们下游性能的偏差很小(Unit Scaling的BERT Base略低于基线,BERT Large略高于基线)。
FP8的实现是基于Graphcore、AMD和Qualcomm最近提出的标准化格式。Graphcore研究之前证明了在FP8中训练损失缩放BERT而没有退化[5],论文也证明了通过Unit Scaling也可以实现同样的效果。
要使FP8优于FP16,不需要额外的技术。只是简单地将matmul输入量化到FP8中,并能够准确地训练(FP8 E4变体中的权重和激活,以及E5中的梯度)。
低精度训练的未来
随着支持FP8的硬件在人工智能社区的采用越来越多,有效、直接且有原则的模型缩放方法也变得越来越重要。Unit Scaling可以适用于广泛的模型和优化器,并且计算开销最小。
下一代大型模型可能会广泛使用低精度格式,所以这种缩放的方法非常的必要。低精度训练的效率优势是巨大的,Unit Scaling也证明了低精度并不一定会 降低模型的表现。
论文地址:https://arxiv.org/abs/2303.11257
引用
[1] P. Micikevicius et al., Mixed precision training (2018). 6th International Conference on Learning Representations
[2] O. Kuchaiev et al., Mixed-precision training for nlp and speech recognition with openseq2seq (2018), arXiv preprint arXiv:1805.10387
[3] P. Micikevicius et al., FP8 formats for deep learning (2022). arXiv preprint arXiv:2209.05433
[4] J. Devlin et al., BERT: Pre-training of deep bidirectional transformers for language understanding (2019). NAACL-HLT
[5] B. Noune et al., 8-bit numerical formats for deep neural networks (2019). arXiv preprint arXiv:2206.02915
本文作者:Charlie Blake