动手学深度学习——卷积层

从全连接到卷积

1、简单例子：分类猫和狗的图片

使用一个还不错的相机采集图片（12M像素）

RGB图片有36M元素

使用100大小的单隐藏层MLP，模型有3.6B元素，远多于世界上所有猫和狗总数（900M狗，600M猫）

2、重新考察全连接层

将输入和输出变形为矩阵（宽度，高度）；将权重变形为4-D张量（h,w）到（h‘，w’）

V是W的重新索引

3、二维交叉相关

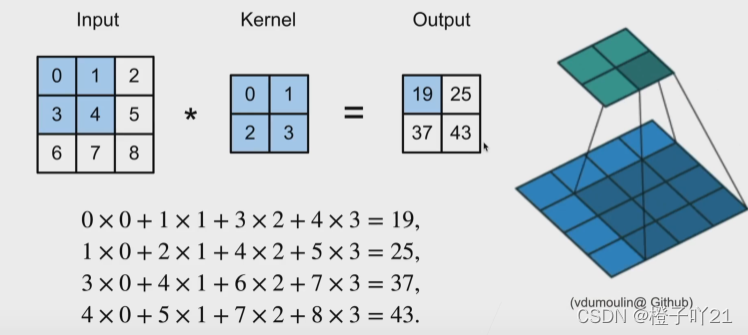
4、二维卷积层

5、 交叉相关和卷积

由于对称性，在实际应用中没有任何区别。

6、一维和三维交叉相关

一维：文本、语言、时序序列。

二维：就是主要应用在图片上。

三维：视频、医学图像、气象地图。

总结：

卷积层将输入和核矩阵进行价交叉相关，加上偏移后得到输出；核矩阵和偏移是科学系的参数；核矩阵的大小是超参数。

代码实现：

import torch
from torch import nn

"""二维互相关运算"""
def corr2d(X, K):
     h, w = K.shape #行数和列数
     Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
     for i in range(Y.shape[0]):
         for j in range(Y.shape[1]):
               Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
     return Y
#构造数组X和核数组K
X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
K = torch.tensor([[0, 1], [2, 3]])
print(corr2d(X, K))

"""
二维卷积层
⼆维卷积层将输⼊和卷积核做互相关运算，并加上⼀个标量偏差来得到输出。卷积层的模型参数包括了卷积核和标量偏差。
在训练模型的时候，通常我们先对卷积核随机初始化，然后不断迭代卷积核和偏差。
下⾯基于 corr2d 函数来实现⼀个⾃定义的⼆维卷积层。
在构造函数 __init__ ⾥我们声明 weight和 bias 这两个模型参数。
前向计算函数 forward 则是直接调⽤ corr2d 函数再加上偏差。
"""
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size)) #取一个随机值，是一个可学的参数，kernel_size就是一个超参数。3x3的矩阵。
        self.bias = nn.Parameter(torch.randn(1))#偏移，标量，初始化为0.
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias
#卷积窗⼝形状为pxq 的卷积层称为 pxq卷积层。同样，pxq 卷积或 pxq卷积核说明卷积核的⾼和宽分别为 p和q 。

"""图像中物体边缘检测"""
"""卷积层的简单应⽤：检测图像中物体的边缘，即找到像素变化的位置。⾸先我们构造
⼀张6x8 的图像（即⾼和宽分别为6像素和8像素的图像）。它中间4列为⿊（0），其余为⽩（1）"""
X=torch.ones(6,8) #构造一个6*8的数组
X[:,2:6]=0  #每一行的第二个元素到第六个元素为0
print(X)
""" 构造⼀个⾼和宽分别为1和2的卷积核K,当它与输⼊做互相关运算时，如果横向相邻元素相同，输出为0；否则输出为⾮0"""
K=torch.tensor([[1,-1]])
print(K)
"""将输⼊ X 和我们设计的卷积核 K 做互相关运算"""
Y=corr2d(X,K)
print(Y)

"""通过数据学习核数组"""
"""，它使⽤物体边缘检测中的输⼊数据 X 和输出数据 Y 来学习我们构造的核数组K 。
我们⾸先构造⼀个卷积层，其卷积核将被初始化成随机数组。
接下来在每⼀次迭代中，我们使⽤平⽅误差来⽐较 Y 和卷积层的输出，然后计算梯度来更新权重。"""
# 构造⼀个核数组形状是(1, 2)的⼆维卷积层
conv2d = Conv2D(kernel_size=(1, 2))

step = 20 #迭代次数
lr = 0.01
for i in range(step):
    Y_hat = conv2d(X)
    l = ((Y_hat - Y) ** 2).sum()
    l.backward()

 # 梯度下降
    conv2d.weight.data -= lr * conv2d.weight.grad
    conv2d.bias.data -= lr * conv2d.bias.grad

 # 梯度清0
    conv2d.weight.grad.fill_(0)
    conv2d.bias.grad.fill_(0)
    if (i + 1) % 5 == 0:
        print('Step %d, loss %.3f' % (i + 1, l.item()))
#输出学习到的卷积核的参数
print("weight: ", conv2d.weight.data)
print("bias: ", conv2d.bias.data)