SVM(Support Vector Machines)支持向量机算法原理以及应用详解+Python代码实现

前言

博主大大小小参与过数十场数学建模比赛，SVM经常在各种建模比赛的优秀论文上见到该模型，一般直接使用SVM算法是比较少的，现在都是在此基础理论之上提出优化算法。但是SVM的基础理论是十分重要的思想，放眼整个分类算法中，SVM是最好的现成的分类器。这里说的‘现成’指的是分类器不加修改即可直接使用。在神经网络没有出现之前，SVM的优化模型可以算得上是预测分类神器了，在机器学习中SVM仍旧是最为出名的算法之一了，本篇博客将致力于将SVM算法以及原理每一个知识点都讲明白，希望没有讲明白的点大家可以在评论区指出。

一、引论

我们使用SVM支持向量机一般用于分类，得到低错误率的结果。SVM能够对训练集意外的数据点做出很好的分类决策。那么首先我们应该从数据层面上去看SVM到底是如何做决策的，这里来看这样一串数据集集合在二维平面坐标系上描绘的图：

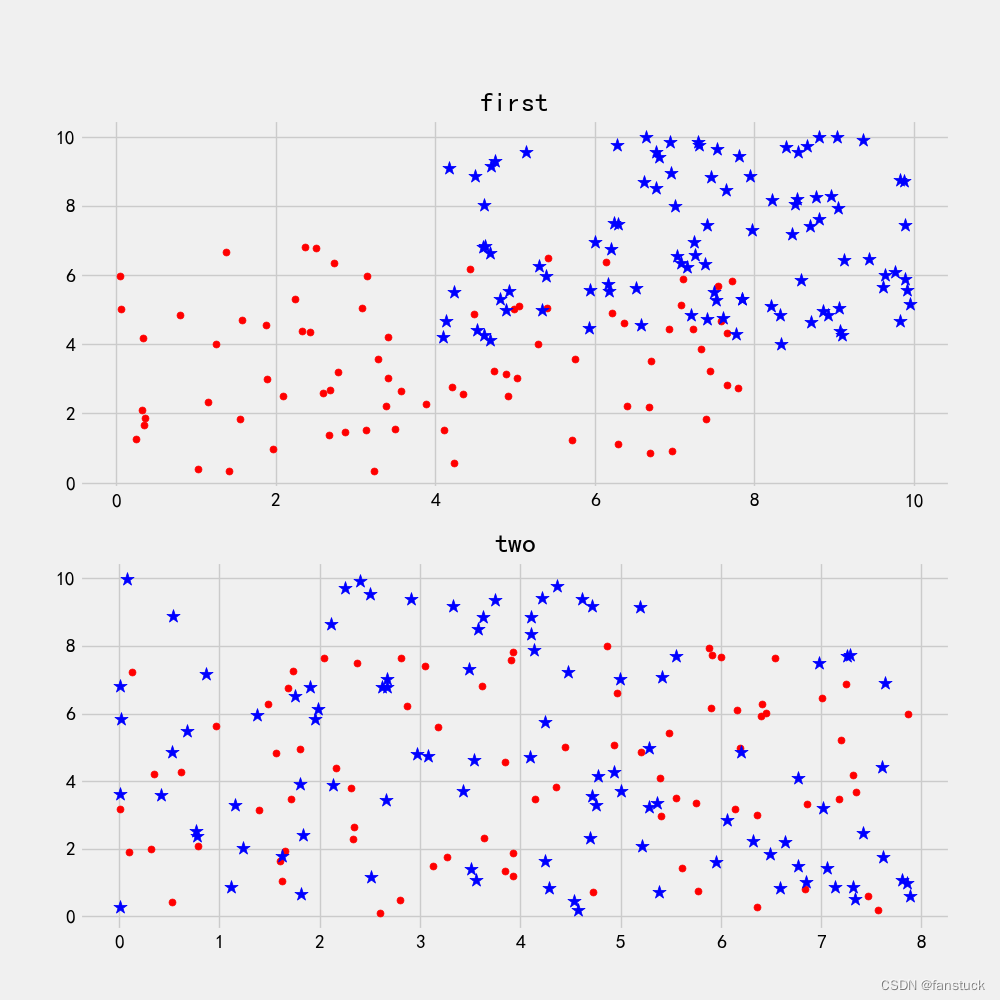
现在我们需要考虑，是否能够画出一条直线将圆形点和星星点分开。像first第一张图片来看，圆点和星点就分的很开，很容易就可以在图中画出一条直线将两组数据分开。而看第二张图片，圆点和星点几乎都聚合在一起，要区分的话十分困难。

我们要划线将他们区分开来的话，有有无数条可以画，但是我们难以找到一条最好区分度最高的线条将它们几乎完全区分。那么在此我们需要了解两个关于数据集的基本概念：

二、理论铺垫

线性可分性（linear separability）

第一张图片的数据就是线性可分的，肉眼可见的线性可分。而第二张图片的数据一看就是线性不可分的。当然我们这样直率的观测也没有错，但是这仅是建立在二维平面数据可视化的基础之上，若是特征维度更高，例如：

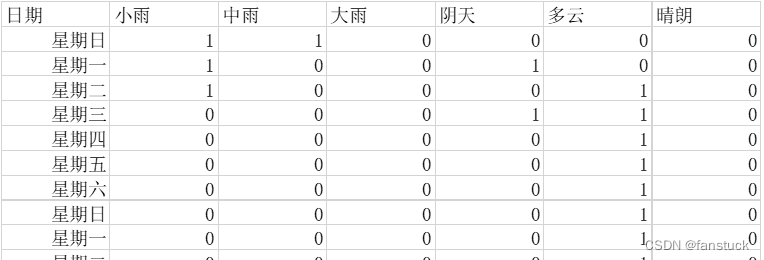
超出我们可视化的技术之外我们如何判断他们是否可分呢？

所有要判断线性可分性需要对线性可分性下个定义：

在分类问题中给定输入数据和学习目标： $X=\left \{ x_{1},...,x_{N} \right \}$ , $y=\left \{ y_{1},...,y_{N} \right \}$ ,其中输入数据的每个样本都包含多个特征并由此构成特征空间（feature space）： $X=\left [ x_{1},...,x_{N} \right ]\epsilon x$ ,而学习目标为二元变量 $y\epsilon \left \{ -1,1 \right \}$ 表示负类（negative class）和正类（positive class）。

若输入数据所在的特征空间存在作为决策边界（decision boundary）的超平面将学习目标按正类和负类分开，并使任意样本的点到平面距离(point to plane distance)大于等于1：

decision boundary： $\omega ^{X}+b=0$

point to plane distance: $y_{i}\left ( \omega ^{T}+b \right )\geq 1$

则称该分类问题具有线性可分性，参数 $\omega$ ,分别为超平面的法向量和截距。

到这里肯定有很多小伙伴会问啥是决策边界什么是超平面啊，莫慌马上给出定义：

超平面

而对机器学习来说，涉及的多是高维空间（多维度）的数据分类，高维空间的SVM，即为超平面。机器学习的最终目的就是要找到最合适的（也即最优的）一个分类超平面（Hyper plane），从而应用这个最优分类超平面将特征数据很好地区分为两类。

大家看图就懂了：

在数学中，超平面（Hyperplane）是n维欧式空间中余维度等于1的线性子空间。这是平面中的直线、空间中的平面之推广。设F为域（可考虑 $F=R$ ）。

n维空间 $F^{n}$ 中的超平面是由方程：

$a_{1}x_{1}+...+a_{n}x_{n}=b$

定义的子集，其中 $a_{1},....,a_{n}\epsilon F$ 是不全为零的常数。

在线性代数的脉络下，F-矢量空间V中的超平面是指形如： $\left \{ v\epsilon V:f\left ( v \right )=0 \right \}$

的子空间，其中 $f:V\rightarrow F$ 是任一非零的线性映射。

在射影几何中，同样可定义射影空间 $P^{n}$ 中的超平面。在齐次坐标（ $x_{0}:...:x_{n}$ )下超平面可由以下方程定义：

$a_{1}x_{1}+...+a_{n}x_{n}=0$ ，其中 $a_{0},...,a_{n}$ 是不全为零的常数。

总而言之：超平面H是从n维空间到n-1维空间的一个映射子空间，它有一个n维向量和一个实数定义。设d是n维欧式空间R中的一个非零向量，a是实数，则R中满足条件dX=a的点X所组成的集合称为R中的一张超平面。

决策边界

SVM是一种优化的分类算法，其动机是寻找一个最佳的决策边界，使得从决策边界与各组数据之间存在margin，并且需要使各侧的margin最大化。那么这个决策边界就是不同类之间的界限。

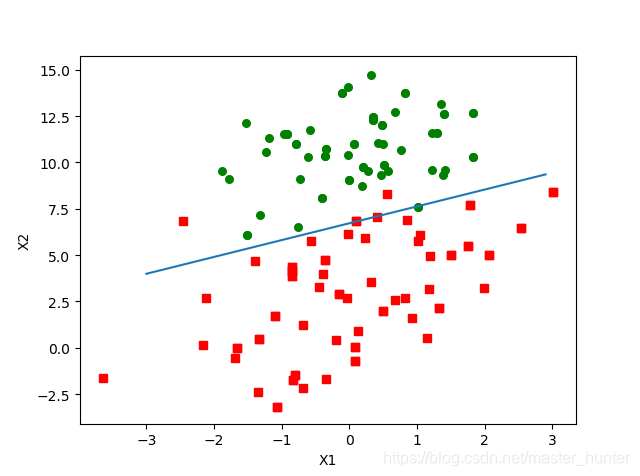
总而言之：在具有两个类的统计分类问题中，决策边界或决策表面是超平面，其将基础向量空间划分为两个集合，一个集合。分类器将决策边界一侧的所有点分类为属于一个类，而将另一侧的所有点分类为属于另一个类。

支持向量（support vector）

在了解了超平面和决策边界我们发现SVM的核心任务是找到一个超平面作为决策边界。那么满足该条件的决策边界实际上构造了2个平行的超平面作为间隔边界以判别样本的分类：

所有在上间隔边界上方的样本属于正类，在下间隔边界下方的样本属于负类。两个间隔边界的距离 $d=\frac{2}{\left \| \omega \right \|}$ 被定义为边距（margin），位于间隔边界上的正类和负类样本为支持向量（support vector）。

损失函数（loss function）

拿我们的first的数据集来看：

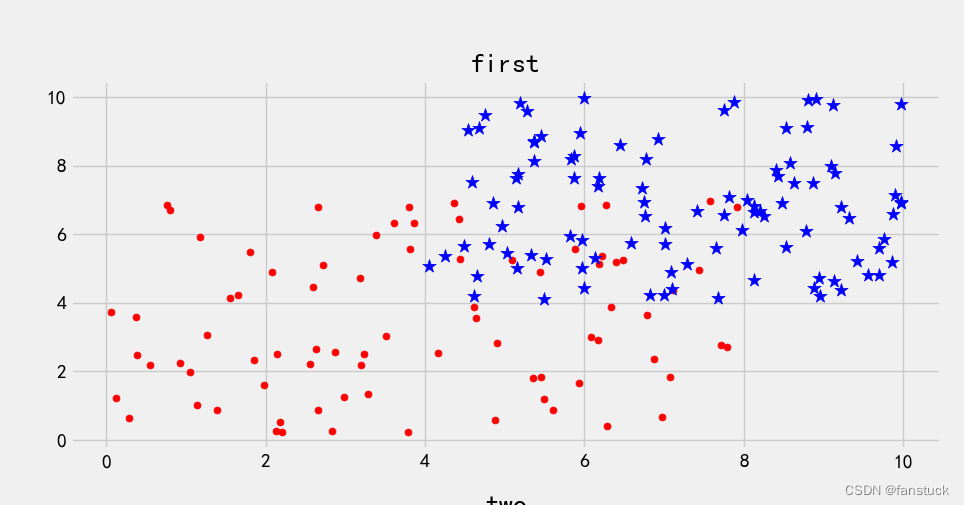
无论我们怎么画直线总有损失的点没有正确分类到。在一个分类问题不具有线性可分性时，使用超平面作为决策边界会带来分类损失，即部分支持向量不再位于间隔边界上，而是进入了间隔边界内部，或落入决策边界的错误一侧。

损失函数可以对分类损失进行量化，其按数学意义可以得到的形式是0-1损失函数：

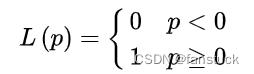
0-1损失函数是一个不连续的分段函数，不利于求解其最小化问题，因此在应用可构造其代理损失（surrogate loss）。代理损失是与原损失函数具有相合性（consistency）的损失函数，最小化代理损失所得的模型参数也是最小化原损失函数的解。也就是说我们需要损失函数计算最小的决策边界。这里给出二元分类（binary classification）中0-1损失函数的代理损失：
名称表达式铰链损失函数（hinge loss function） $L\left ( y\hat{},y \right )=max(0,1-y\hat{}y)$ 交叉熵损失函数（cross-entropy loss function） $L\left ( y\hat{},y \right )=-ylog(y\hat{})-(1-y)log(1-y\hat{})$ 指数损失函数（exponential loss function） $L\left ( y\hat{},y \right )=exp(-y\hat{}y)$
SVM使用的是铰链损失函数: $L(p)=max(0,1-p)$ .

经验风险（empirical risk）与结构风险（structural risk）

按统计学习理论，分类器在经过学习并应用于新数据时会产生风险，风险的类型可分为经验风险和结构风险。

empirical risk：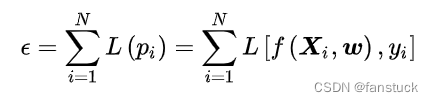

structural risk：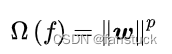

式中 $f$ 表示分类器，经验风险由损失函数定义，描述了分类器所给出的分类结果的准确程度；结构风险由分类器参数矩阵的范数定义，描述了分类器自身的复杂程度以及稳定程度，复杂的分类器容易产生过拟合，因此是不稳定的。若一个分类器通过最小化经验风险和结构风险的线性组合以确定其模型参数：

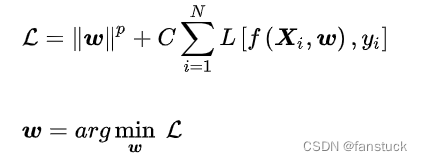
则对该分类器的求解是一个正则化问题，常数 $C$ 是正则化系数。当 $p$ =2时，该式被称为 $L_{2}$ 正则化或Tikhonov正则化（Tikhonov regularization）。SVM的结构风险 $p=2$ 表示，在线性可分问题下硬边界SVM的经验风险可以归0，因此其是一个完全最小化结构风险的分类器；在线性不可分问题中，软边界SVM的经验风险不可归0，因此其是一个 $L_{2}$ 正则化分类器，最小化结构风险和经验风险的线性组合。

核方法

一些线性不可分的问题可能是非线性可分的，即特征空间存在超平面将正类和负类分开。使用非线性函数可以将非线性可分问题从原始的特征空间映射至更高维的空间（希尔伯特空间（Hilbert space） $H$ ）从而转化为线性可分问题，此时作为决策边界的超平面表示如下：

$\omega ^{T}\phi (X)+b=0$

式中 $\phi :X\rightarrow H$ 为映射函数。由于映射函数具有复杂的形式，难以计算其内积，因此可使用核方法（kernel method），即定义映射函数的内积为核函数：

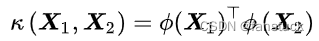
以回避内积的显式计算。

常见的核函数

名称解析式多项式核（polynomial kernel） $\kappa (X_{1},X_{2})=(X_{1}^T,X_{2})^n$ 径向基函数核（RBF kernel） $\kappa (X_{1},X_{2})=exp(-\frac{\left \| X_{1}-X_{2} \right \|^2}{2\delta ^2})$ 拉普拉斯核（Laplacian kernel） $\kappa (X_{1},X_{2})=exp(-\frac{\left \| X_{1}-X_{2} \right \|}{\delta })$ Sigmoid核（Sigmoid kernel） $\kappa (X_{1},X_{2})=tanh[a(X_{1}^TX_{2})-b], a,b>0$
当多项式核的阶为1时，其被称为线性核，对应的非线性分类器退化为线性分类器。RBF核也被称为高斯核（Gaussian kernel），其对应的映射函数将样本空间映射至无限维空间。

三、算法流程

在了解了上述算法原理以后，我们便对SVM算法有了个大致清晰的认知，那么SVM是如何挖掘到损失最小的超平面的呢？

SVM的求解可以使用二次凸优化问题的数值方法，例如内点法（Interior Point Method, IPM）和序列最小优化算法（Sequential Minimal Optimization, SMO），在拥有充足学习样本时也可使用随机梯度下降。

这里我们采用SMO序列最小优化算法计算：

SMO序列最小优化算法

SMO是一种坐标下降法（coordinate descent）以迭代方式求解SVM的对偶问题，其设计是在每个迭代步选择拉格朗日乘子中的两个变量 $\alpha _{i},\alpha _{j}$ 并固定其他参数，将原优化问题简化至一维子可行域，此时约束条件有如下等价形式：

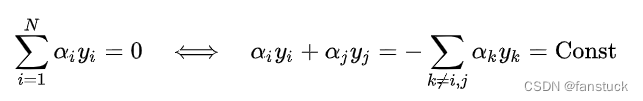
将上式右侧带入SVM的对偶问题并消去求和项中的 $\alpha _{j}$ 可以得到仅关于 $a_{i}$ 的二次规划问题，该优化问题有闭式解可以快速计算。在此基础上，SMO有如下计算框架:

初始所有化拉格朗日乘子；
识别一个不满足KKT条件的乘子，并求解其二次规划问题；
反复执行上述步骤直到所有乘子满足KKT条件或参数的更新量小于设定值。

可以证明，在二次凸优化问题中，SMO的每步迭代都严格地优化了SVM的对偶问题，且迭代会在有限步后收敛于全局极大值。SMO算法的迭代速度与所选取乘子对KKT条件的偏离程度有关，因此SMO通常采用启发式方法选取拉格朗日乘子。

Python sklearn代码实现：

为了方便展示效果，我们仍旧用first的数据集进行：

sklearn.svm.SVC语法格式为：

class sklearn.svm.SVC(  *, 
                        C=1.0, 
                        kernel='rbf',
                        degree=3, 
                        gamma='scale', 
                        coef0=0.0, 
                        shrinking=True, 
                        probability=False, 
                        tol=0.001, 
                        cache_size=200, 
                        class_weight=None, 
                        verbose=False, 
                        max_iter=- 1, 
                        decision_function_shape='ovr', 
                        break_ties=False, 
                        random_state=None)

该实现基于 libsvm，更多详细信息可以去官网上查阅：sklearn.svm.SVC.

# 导入模块
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# 鸢尾花数据
iris = datasets.load_iris()
X = iris.data[:, :2] # 为便于绘图仅选择2个特征
y = iris.target
# 测试样本（绘制分类区域）
xlist1 = np.linspace(X[:, 0].min(), X[:, 0].max(), 200)
xlist2 = np.linspace(X[:, 1].min(), X[:, 1].max(), 200)
XGrid1, XGrid2 = np.meshgrid(xlist1, xlist2)
# 非线性SVM：RBF核，超参数为0.5，正则化系数为1，SMO迭代精度1e-5, 内存占用1000MB
svc = svm.SVC(kernel='rbf', C=1, gamma=0.5, tol=1e-5, cache_size=1000).fit(X, y)
# 预测并绘制结果
Z = svc.predict(np.vstack([XGrid1.ravel(), XGrid2.ravel()]).T)
Z = Z.reshape(XGrid1.shape)
plt.contourf(XGrid1, XGrid2, Z, cmap=plt.cm.hsv)
plt.contour(XGrid1, XGrid2, Z, colors=('k',))
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', linewidth=1.5, cmap=plt.cm.hsv)
plt.show()

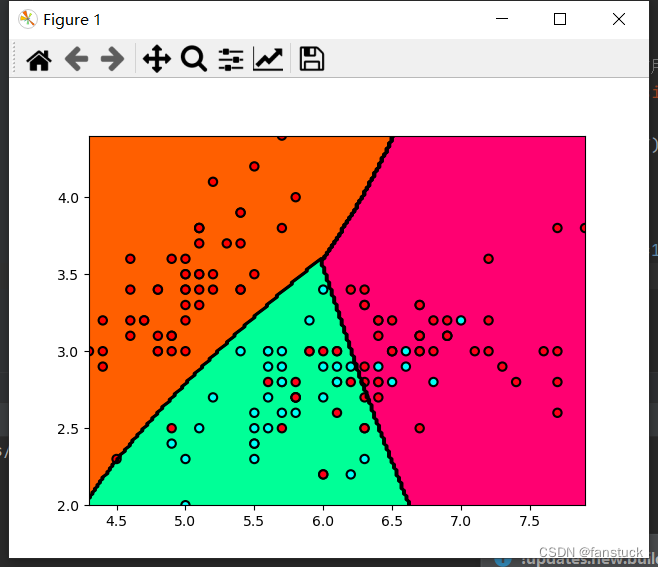
Python源代码实现+手写字识别分类：

from numpy import *

def selectJrand(i, m):  # 在某个区间范围内随机选择一个整数
    # i为第一个alhpa的下表，m是所有alpha的数目
    j = i  # we want to select any J not equal to i
    while (j == i):
        j = int(random.uniform(0, m))
    return j

def clipAlpha(aj, H, L):  # 在数值太大的时候对其进行调整
    # aj是H是下限，是L的上限
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

def kernelTrans(X, A, kTup):  # calc the kernel or transform data to a higher dimensional space
    # X是数据，A是
    m, n = shape(X)
    K = mat(zeros((m, 1)))
    # 这里为了简单，我们只内置了两种核函数，但是原理是一样的，需要的话再写其他类型就是了
    # 线性核函数：k(x,x_i)=x*x_i,它不需要再传入参数。
    if kTup[0] == 'lin':
        K = X * A.T  # linear kernel，线性核函数
    elif kTup[0] == 'rbf':  # 高斯核函数，传入的参数作为detla
        for j in range(m):
            deltaRow = X[j, :] - A
            K[j] = deltaRow * deltaRow.T  # 2范数
        K = exp(K / (-1 * kTup[1] ** 2))  # divide in NumPy is element-wise not matrix like Matlab
        # numpy中，/表示对矩阵元素进行计算而不是计算逆（MATLAB）
    else:
        raise NameError('Houston We Have a Problem -- \
    That Kernel is not recognized')  
    return K

# 定义了一个类来进行SMO算法
class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters
        # kTup储存核函数信息，它是一个元组，元组第一个元素是一个描述核函数类型的字符串，其他两个元素是核函数可能需要的参数
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]  # m是样本个数，也是a的个数
        self.alphas = mat(zeros((self.m, 1)))  # 初始化a序列，都设置为0
        self.b = 0
        # 第一列给出的是eCache是否有效的标志位，而第二位是实际的E值
        self.eCache = mat(zeros((self.m, 2)))  # first column is valid flag
        # 如果第一位是1，说明现在的这个Ek是有效的
        self.K = mat(zeros((self.m, self.m)))  # 使用核函数计算后的数据，就是内积矩阵，方便直接调用内积结果
        for i in range(self.m):
            self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)

def calcEk(oS, k):  # 计算第k个样本的Ek
    fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

def selectJ(i, oS, Ei):  # this is the second choice -heurstic, and calcs Ej
    # 选定了a_1之后选择a_2
    # 选择a_2
    maxK = -1;
    maxDeltaE = 0;
    Ej = 0  # 选择|E1-E2|最大的E2并返回E2和j
    # 先将E1存进去，以便于之后的统一化进行
    oS.eCache[i] = [1, Ei]  # set valid #choose the alpha that gives the maximum delta E
    '''
    numpy函数返回非零元素的目录。
    返回值为元组， 两个值分别为两个维度， 包含了相应维度上非零元素的目录值。   
    可以通过a[nonzero(a)]来获得所有非零值。
    .A的意思是：getArray(),也就是将矩阵转换为数组
    '''
    # 获取哪些样本的Ek是有效的，ValidEcacheList里面存的是所有有效的样本行Index
    validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
    # 对每一个有效的Ecache都比较一遍
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:  # loop through valid Ecache values and find the one that maximizes delta E
            if k == i: continue  # don't calc for i, waste of time
            # 如果选到了和a1一样的，就继续，因为a1和a2必须选不一样的样本
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k;
                maxDeltaE = deltaE;
                Ej = Ek
        return maxK, Ej
    else:  # in this case (first time around) we don't have any valid eCache values
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

def updateEk(oS, k):  # after any alpha has changed update the new value in the cache
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]
    # 计算Ek并保存在类oS中

# 内循环寻找合适的a_2
def innerL(i, oS):
    Ei = calcEk(oS, i)  # 为什么这里要重新算呢？因为a_1刚刚更新了，和存储的不一样
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or (
            (oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 如果a1选的合适的话，不合适就直接结束了
        # 剩下的逻辑都一样，只不过不是使用x_ix_j，而是使用核函数
        j, Ej = selectJ(i, oS, Ei)  # this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy();
        alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H: print("L==H"); return 0
        eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j]  # changed for kernel
        if eta >= 0: print("eta>=0"); return 0
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        updateEk(oS, j)  # added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])  # update i by the same amount as j
        updateEk(oS, i)  # added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (
                    oS.alphas[j] - alphaJold) * oS.K[i, j]
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (
                    oS.alphas[j] - alphaJold) * oS.K[j, j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0

def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):  # 默认核函数是线性，参数为0（那就是它本身了）
    # 这个kTup先不管，之后用
    oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup)  # 初始化这一结构
    iter = 0
    # entireSet是控制开关，一次循环对所有样本点都遍历，第二次就只遍历非边界点
    entireSet = True;
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged: int = 0
        if entireSet:  # go over all
            for i in range(oS.m):
                alphaPairsChanged += innerL(i, oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1
        else:  # go over non-bound (railed) alphas
            # 把大于0且小于C的a_i挑出来，这些是非边界点，只从这些点上遍历
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1
        # 如果第一次是对所有点进行的，那么第二次就只对非边界点进行

        # 如果对非边界点进行后没有，就在整个样本上进行
        '''
        首先在非边界集上选择能够使函数值足够下降的样本作为第二个变量，
        如果非边界集上没有，则在整个样本集上选择第二个变量，
        如果整个样本集依然不存在，则重新选择第一个变量。
        '''
        if entireSet:  # 遍历一次后改为非边界遍历
            entireSet = False
        elif (alphaPairsChanged == 0):  # 如果alpha没有更新,计算全样本遍历
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b, oS.alphas

# 利用SVM进行分类，返回的是函数间隔，大于0属于1类，小于0属于2类。
def calcWs(alphas, dataArr, classLabels):
    X = mat(dataArr);
    labelMat = mat(classLabels).transpose()
    m, n = shape(X)
    w = zeros((n, 1))
    for i in range(m):
        w += multiply(alphas[i] * labelMat[i], X[i, :].T)
    return w

# 将图像转换为向量
def img2vector(filename):
    # 一共有1024个特征
    returnVect = zeros((1, 1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0, 32 * i + j] = int(lineStr[j])
    return returnVect

def loadImages(dirName):
    from os import listdir
    hwLabels = []
    # 利用listdir读文件名，这里的label写在了文件名里面
    trainingFileList = listdir(dirName)  # load the training set
    m = len(trainingFileList)
    trainingMat = zeros((m, 1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]  # take off .txt
        classNumStr = int(fileStr.split('_')[0])
        if classNumStr == 9:
            hwLabels.append(-1)
        else:
            hwLabels.append(1)
        trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr))
    return trainingMat, hwLabels

# 手写识别问题
def testDigits(kTup=('rbf', 10)):
    dataArr, labelArr = loadImages('trainingDigits')
    b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
    datMat = mat(dataArr);
    labelMat = mat(labelArr).transpose()
    svInd = nonzero(alphas.A > 0)[0]
    sVs = datMat[svInd]
    labelSV = labelMat[svInd];
    print("there are %d Support Vectors" % shape(sVs)[0])
    m, n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
        predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]): errorCount += 1
    print("the training error rate is: %f" % (float(errorCount) / m))
    dataArr, labelArr = loadImages('testDigits')
    errorCount = 0
    datMat = mat(dataArr);
    labelMat = mat(labelArr).transpose()
    m, n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
        predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
        if sign(predict) != sign(labelArr[i]): errorCount += 1
    print("the test error rate is: %f" % (float(errorCount) / m))
testDigits(kTup=('rbf', 20))

点关注，防走丢，如有纰漏之处，请留言指教，非常感谢

以上就是本期全部内容。我是fanstuck ，有问题大家随时留言讨论，我们下期见。

参阅：

SVM通俗详解

SVM百度百科

损失函数百度百科

超平面百度百科

标签：算法 python 机器学习

本文转载自: https://blog.csdn.net/master_hunter/article/details/125691694
版权归原作者 fanstuck 所有，如有侵权，请联系我们删除。