YOLOv5：IoU、GIoU、DIoU、CIoU、EIoU
前言
- 由于本人水平有限，难免出现错漏，敬请批评改正。
- 更多精彩内容，可点击进入YOLO系列专栏或我的个人主页查看
前提条件
- 熟悉Python
相关介绍
- Python是一种跨平台的计算机程序设计语言。是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。最初被设计用于编写自动化脚本(shell)，随着版本的不断更新和语言新功能的添加，越多被用于独立的、大型项目的开发。
- PyTorch 是一个深度学习框架，封装好了很多网络和深度学习相关的工具方便我们调用，而不用我们一个个去单独写了。它分为 CPU 和 GPU 版本，其他框架还有 TensorFlow、Caffe 等。PyTorch 是由 Facebook 人工智能研究院（FAIR）基于 Torch 推出的，它是一个基于 Python 的可续计算包，提供两个高级功能：1、具有强大的 GPU 加速的张量计算（如 NumPy）；2、构建深度神经网络时的自动微分机制。
IoU（Intersection over Union）
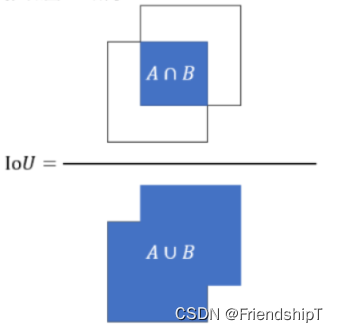
- 交并比（IoU）是一种用于衡量两个边界框之间重叠程度的指标。它是通过计算两个边界框的交集面积与并集面积之比来计算的。在目标检测中，IoU通常用于衡量预测框和真实框之间的重叠程度，以评估目标检测算法的准确性。如果IoU值越高，则表示预测框和真实框之间的重叠程度越高，因此预测结果越准确。
- 优点： - IoU是目标检测中最常用的指标之一，可以用来评价目标检测算法的准确性。 IoU可以帮助我们确定正样本和负样本。- IoU可以帮助我们评估输出框（predict box）和ground truth box之间的重叠程度。
- 缺点： - IoU只能衡量两个边界框之间的重叠程度，不能衡量其他因素，如形状、颜色等。- IoU不适用于所有类型的目标检测任务。
由于
I
o
U
IoU
IoU的公式定义，作为损失函数会出现的问题。比如，
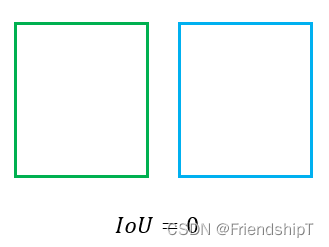
- 当预测框和目标框不相交时，IoU=0，无法反应两个框距离的远近，此时损失函数不可导，IoU无法优化两个框不相交的情况。
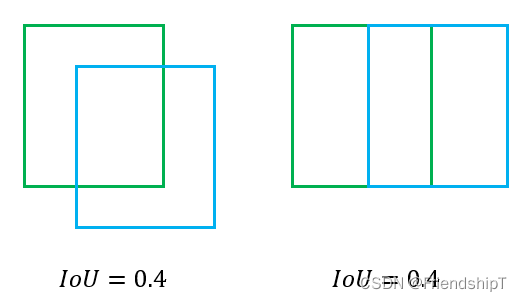
- 当IoU也相同时，会出现预测框和目标框相交位置不一样的情况，IoU无法区分两者相交情况的不同。
GIoU（Generalized-IoU）
- 在CVPR2019中，论文《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》 的提出了GIoU的思想。由于IoU是比值的概念，对目标物体的scale是不敏感的。然而检测任务中的BBox的回归损失(MSE loss, l1-smooth loss等）优化和IoU优化不是完全等价的，而且 Ln 范数对物体的scale也比较敏感，IoU无法直接优化没有重叠的部分。
- GIoU是一种用于目标检测的损失函数，它是IoU的改进版。GIoU的全称是Generalized Intersection over Union，它是一种度量和损失函数，用于衡量两个边界框之间的重叠程度。GIoU的目标是在损失函数中加入一个ground truth和预测框构成的闭包的惩罚，它的惩罚项是闭包减去两个框的并集后的面积在闭包中的比例越小越好。GIoU中，增加了相交尺度的衡量方式。
- 公式： G I o U = I o U − ∣ A c − U ∣ ∣ A c ∣ GIoU=IoU-\frac{|A_c-U|}{|A_c|} GIoU=IoU−∣Ac∣∣Ac−U∣ 公式的含义：先计算两个框的最小闭包区域面积 A c A_c Ac（即同时包含了预测框和真实框的最小框的面积），再计算出 I o U IoU IoU，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用 I o U IoU IoU减去这个比重得到 G I o U GIoU GIoU。
- 优点： - 它能够反映检测效果，即使在没有重叠区域的情况下，它也能够反映检测效果。- GIoU损失函数的目标是在损失函数中加入一个ground truth和预测框构成的闭包的惩罚，它的惩罚项是闭包减去两个框的并集后的面积在闭包中的比例越小越好。
- 缺点： - 计算量大，因为它需要计算两个框之间的交集和并集。此外，GIoU对于小目标和大目标之间的距离不敏感，这可能会导致一些问题.
由于
G
I
o
U
GIoU
GIoU的公式定义，作为损失函数
L
G
I
o
U
=
1
−
G
I
o
U
L_{GIoU}=1-GIoU
LGIoU=1−GIoU会出现的问题。比如，
- 预测框在目标框内部且预测框大小一致的情况，这时预测框和目标框的差集都是相同的，因此这三种状态的GIoU值也都是相同的，这时GIoU退化成了IoU，无法区分相对位置关系。
DIoU（Distance-IoU）
- DIoU是GIoU的改进版，它考虑了目标框和anchor之间的距离、重叠率和尺度，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。 基于IoU和GIoU存在的问题，作者提出了两个问题： - 直接最小化anchor框与目标框之间的归一化距离是否可行，以达到更快的收敛速度？- 如何使回归在与目标框有重叠甚至包含时更准确、更快？
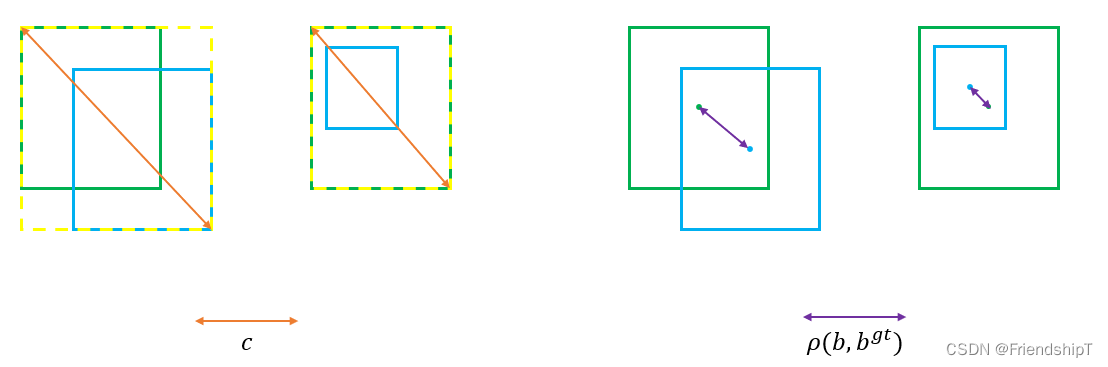
- 公式： D I o U = I o U − ρ 2 ( b , b g t ) c 2 DIoU=IoU-\frac{\rho2(b,b^{gt})}{c^2} DIoU=IoU−c2ρ2(b,bgt)
- 其中， b , b g t b,b^{gt} b,bgt 分别代表了预测框和真实框的中心点，且 ρ \rho ρ代表的是计算两个中心点间的欧式距离， c c c代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。
- 优点： - 它能够反映检测效果，即使在没有重叠区域的情况下，它也能够反映检测效果。- DIoU对于小目标和大目标之间的距离更加敏感，这可能会解决GIoU存在的问题。
由于
D
I
o
U
DIoU
DIoU的公式定义，作为损失函数
L
D
I
o
U
=
1
−
D
I
o
U
L_{DIoU}=1-DIoU
LDIoU=1−DIoU会出现的问题。比如，
- DIoU考虑了重叠面积和中心点距离，当目标框包裹预测框的时候，直接度量2个框的距离，因此DIoU收敛的更快，但并没有考虑到长宽比。
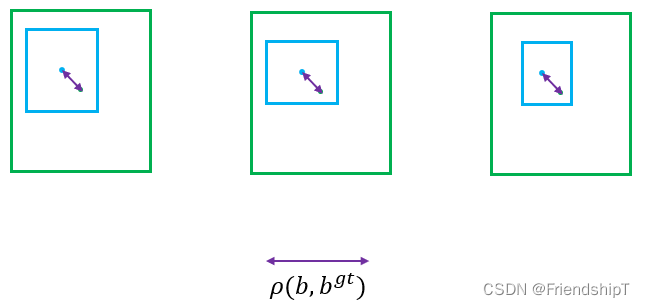从上图可以看到，不同长宽比的预测框， ρ \rho ρ两个中心点间的欧式距离相同。
CIoU （Complete-IoU）
- CIoU是DIoU的改进版，它在DIoU的基础上加入了长宽比的计算，使得目标框回归更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。
- 公式： C I o U = I o U − ρ 2 ( b , b g t ) c 2 − α v CIoU=IoU - \frac{\rho2(b,b^{gt})}{c^2} - \alpha v CIoU=IoU−c2ρ2(b,bgt)−αv
- 其中， b , b g t b,b^{gt} b,bgt分别代表了预测框和真实框的中心点，\rho代表的是计算两个中心点间的欧式距离， c c c代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离， α \alpha α是权重函数， v v v分别代表了预测框和真实框的长宽比之间的差异。
v v v是衡量长宽比一致性的参数，具体地， v v v的计算公式如下 v = 4 π 2 ( arctan ( w g t h g t ) − arctan ( w p h p ) ) v = \frac{4}{\pi^2}(\arctan(\frac{w^{gt}}{h^{gt}}) - \arctan(\frac{w_p}{h_p})) v=π24(arctan(hgtwgt)−arctan(hpwp)) 其中， w p w_p wp和 h p h_p hp分别代表了预测框的宽和高， w g t w^{gt} wgt和 h g t h^{gt} hgt分别代表了真实框的宽和高。C I o U CIoU CIoU的损失函数为 L C I o U = 1 − C I o U L_{CIoU} = 1 - CIoU LCIoU=1−CIoU
EIoU（Efficient-IoU）
- CIoU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。但是通过其公式中的v反映的纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性。针对这一问题，有学者在CIoU的基础上将纵横比拆开，提出了EIoU Loss，并且加入Focal聚焦优质的锚框，该方法出自于2021年的一篇文章《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》
- 公式： E I o U = I o U − ρ 2 ( b , b g t ) c 2 − ρ 2 ( w , w g t ) c w 2 − ρ 2 ( h , h g t ) c h 2 EIoU=IoU - \frac{\rho2(b,b^{gt})}{c^2} - \frac{\rho2(w,w^{gt})}{c_w^2} - \frac{\rho2(h,h^{gt})}{c_h^2} EIoU=IoU−c2ρ2(b,bgt)−cw2ρ2(w,wgt)−ch2ρ2(h,hgt)
- 其中 C w C_w Cw 和 C h C_h Ch 是覆盖两个Box的最小外接框的宽度和高度。
- EIoU的惩罚项是在CIoU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和锚框的长和宽，该损失函数包含三个部分：重叠损失，中心距离损失，宽高损失，前两部分延续CIoU中的方法，但是宽高损失直接使目标盒与锚盒的宽度和高度之差最小，使得收敛速度更快。EIoU损失函数惩罚项公式如下： L E I o U = 1 − E I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + ρ 2 ( w , w g t ) c w 2 + ρ 2 ( h , h g t ) c h 2 L_{EIoU}=1-EIoU=1- IoU + \frac{\rho2(b,b^{gt})}{c^2} + \frac{\rho2(w,w^{gt})}{c_w^2} + \frac{\rho2(h,h^{gt})}{c_h^2} LEIoU=1−EIoU=1−IoU+c2ρ2(b,bgt)+cw2ρ2(w,wgt)+ch2ρ2(h,hgt)
- 优点： - EIoU在CIoU的基础上分别计算宽高的差异值取代了纵横比。
YOLOv5源代码中加入EIoU
在YOLOv5项目utils\metrics.py代码中，bbox_iou函数只包含GIoU, DIoU, CIoU的计算，
defbbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):# Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
box2 = box2.T
# Get the coordinates of bounding boxesif x1y1x2y2:# x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]else:# transform from xywh to xyxy
b1_x1, b1_x2 = box1[0]- box1[2]/2, box1[0]+ box1[2]/2
b1_y1, b1_y2 = box1[1]- box1[3]/2, box1[1]+ box1[3]/2
b2_x1, b2_x2 = box2[0]- box2[2]/2, box2[0]+ box2[2]/2
b2_y1, b2_y2 = box2[1]- box2[3]/2, box2[1]+ box2[3]/2# Intersection area
inter =(torch.min(b1_x2, b2_x2)- torch.max(b1_x1, b2_x1)).clamp(0)* \
(torch.min(b1_y2, b2_y2)- torch.max(b1_y1, b2_y1)).clamp(0)# Union Area
w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
union = w1 * h1 + w2 * h2 - inter + eps
iou = inter / union
if CIoU or DIoU or GIoU:
cw = torch.max(b1_x2, b2_x2)- torch.min(b1_x1, b2_x1)# convex (smallest enclosing box) width
ch = torch.max(b1_y2, b2_y2)- torch.min(b1_y1, b2_y1)# convex heightif CIoU or DIoU:# Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
c2 = cw **2+ ch **2+ eps # convex diagonal squared
rho2 =((b2_x1 + b2_x2 - b1_x1 - b1_x2)**2+(b2_y1 + b2_y2 - b1_y1 - b1_y2)**2)/4# center distance squaredif CIoU:# https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
v =(4/ math.pi **2)* torch.pow(torch.atan(w2 / h2)- torch.atan(w1 / h1),2)with torch.no_grad():
alpha = v /(v - iou +(1+ eps))return iou -(rho2 / c2 + v * alpha)# CIoUreturn iou - rho2 / c2 # DIoU
c_area = cw * ch + eps # convex areareturn iou -(c_area - union)/ c_area # GIoU https://arxiv.org/pdf/1902.09630.pdfreturn iou # IoU
将EIoU计算加入到源代码中，修改代码如下：
defbbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, EIoU=False, eps=1e-7):# Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
box2 = box2.T
# Get the coordinates of bounding boxesif x1y1x2y2:# x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]else:# transform from xywh to xyxy
b1_x1, b1_x2 = box1[0]- box1[2]/2, box1[0]+ box1[2]/2
b1_y1, b1_y2 = box1[1]- box1[3]/2, box1[1]+ box1[3]/2
b2_x1, b2_x2 = box2[0]- box2[2]/2, box2[0]+ box2[2]/2
b2_y1, b2_y2 = box2[1]- box2[3]/2, box2[1]+ box2[3]/2# Intersection area
inter =(torch.min(b1_x2, b2_x2)- torch.max(b1_x1, b2_x1)).clamp(0)* \
(torch.min(b1_y2, b2_y2)- torch.max(b1_y1, b2_y1)).clamp(0)# Union Area
w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
union = w1 * h1 + w2 * h2 - inter + eps
iou = inter / union
if CIoU or DIoU or GIoU or EIoU:
cw = torch.max(b1_x2, b2_x2)- torch.min(b1_x1, b2_x1)# convex (smallest enclosing box) width
ch = torch.max(b1_y2, b2_y2)- torch.min(b1_y1, b2_y1)# convex heightif CIoU or DIoU or EIoU:# Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
c2 = cw **2+ ch **2+ eps # convex diagonal squared
rho2 =((b2_x1 + b2_x2 - b1_x1 - b1_x2)**2+(b2_y1 + b2_y2 - b1_y1 - b1_y2)**2)/4# center distance squaredif CIoU:# https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
v =(4/ math.pi **2)* torch.pow(torch.atan(w2 / h2)- torch.atan(w1 / h1),2)with torch.no_grad():
alpha = v /(v - iou +(1+ eps))return iou -(rho2 / c2 + v * alpha)# CIoUelif EIoU:
w=(w1-w2)*(w1-w2)
h=(h1-h2)*(h1-h2)return iou-(rho2/c2+w/(cw**2)+h/(ch**2))#EIoU 2021.12.29return iou - rho2 / c2 # DIoU
c_area = cw * ch + eps # convex areareturn iou -(c_area - union)/ c_area # GIoU https://arxiv.org/pdf/1902.09630.pdfreturn iou # IoU
小结
I o U IoU IoU：主要考虑**检测框和目标框重叠面积**。G I o U GIoU GIoU：在 I o U IoU IoU的基础上，解决**边界框不重合(IoU=0)时的问题**。D I o U DIoU DIoU：在 I o U IoU IoU和 G I o U GIoU GIoU的基础上，考虑**边界框中心点距离的信息**，解决 G I o U GIoU GIoU收敛慢的问题C I o U CIoU CIoU：在 D I o U DIoU DIoU的基础上，考虑**边界框宽高比的尺度信息**，提升回归精确度。E I o U EIoU EIoU:考虑了重叠面积，中心点距离、长宽边长真实差，基于 C I o U CIoU CIoU解决了纵横比(宽高比)的模糊。
损失函数优点缺点IoU具有尺度不变性，满足非负性；同一性；对称性；三角不等性等特点。1.如果两个框不相交，不能反映两个框距离远近。2.无法精确的反映两个框的重合度大小GIoU在基于IoU特性的基础上引入最小外接框解决检测框和真实框没有重叠时loss等于0问题。1.当检测框和真实框出现包含现象的时候GIoU退化成IoU。2.两个框相交时，在水平和垂直方向上收敛慢。DIoU在基于IoU特性的基础上考虑到GIoU的缺点，直接回归两个框中心点的欧式距离，加速收敛。回归过程中未考虑Bounding box的纵横比，精确度上尚有进一步提升的空间。CIoUCIoU就是在DIoU的基础上增加了检测框尺度的loss，增加了长和宽的loss，这样预测框就会更加的符合真实框。CIoU就是在DIoU的基础上增加了检测框尺度的loss，增加了长和宽的loss，这样预测框就会更加的符合真实框。EIoUEIoU在CIoU的基础上分别计算宽高的差异值取代了纵横比，同时引入Focal Loss解决难易样本不平衡的问题。——
参考
[1] https://github.com/ultralytics/yolov5
[2] https://arxiv.org/pdf/1902.09630.pdf
[3] https://arxiv.org/pdf/1608.01471.pdf
[4] https://arxiv.org/pdf/1911.08287.pdf
[5] https://arxiv.org/pdf/2101.08158.pdf
[6] https://blog.csdn.net/nan355655600/article/details/106246625
[7] https://zhuanlan.zhihu.com/p/94799295
[8] https://blog.csdn.net/weixin_45751396/article/details/127150065
[9] https://zhuanlan.zhihu.com/p/270663039
- 由于本人水平有限，难免出现错漏，敬请批评改正。
- 更多精彩内容，可点击进入YOLO系列专栏或我的个人主页查看
本文转载自: https://blog.csdn.net/FriendshipTang/article/details/129969044
版权归原作者 FriendshipT 所有， 如有侵权，请联系我们删除。
版权归原作者 FriendshipT 所有， 如有侵权，请联系我们删除。