基于Python实现五大常用分类算法(原理+代码)

读： 在机器学习和统计中，分类算法通过对已知类别训练集的计算和分析，从中发现类别规则并预测新数据的类别。分类被认为是监督学习的一个实例，即学习可以获得正确识别的观察的训练集的情况。

实现分类的算法，特别是在具体实现中，被称为分类器。本文将从实际应用案例出发，总结性介绍几种常用的单模型分类器。原理和代码均在文中，内容较长，建议收藏，后面需要用到时方便查看。

获取更多资源，关注VX公中号：python语言空间

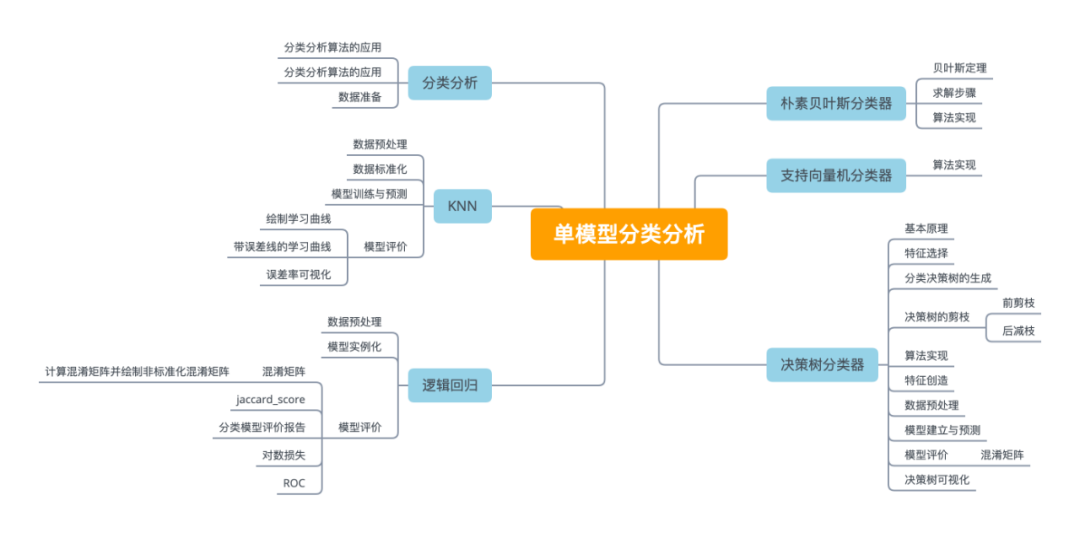
一般应用

分类分析用于提炼应用规则

• 利用构建算法过程中的分类规则；
• 以决策树为例：决策树分类节点表示局部最优化的显著特征值，每个节点下的特征变量以及对应的值的组合构成规则。

分类用于提取特征

• 从大量的输入变量中获得重要性特征，然后提取权重最高的几个特征。

分类用于处理缺失值

• 缺失值是分类变量，基于模型法填补缺失值；
• 基于已有其他字段，将缺失字段作为目标变量进行预测。

分类分析算法的选取

• 文本分类时用到最多的是朴素贝叶斯。
• 训练集比较小，那么选择高偏差且低方差的分类算法效果逢高，如朴素贝叶斯、支持向量机、这些算法不容易过拟合。
• 训练集比较大，选取何种方法都不会显著影响准确度。
• 省时好操作选着用支持向量机，不要使用神经网络。
• 重视算法准确度，那么选择算法精度高的算法，例如支持向量机、随机森林。
• 想得到有关预测结果的概率信息，使用逻辑回归。
• 需要清洗的决策规则，使用决策树。

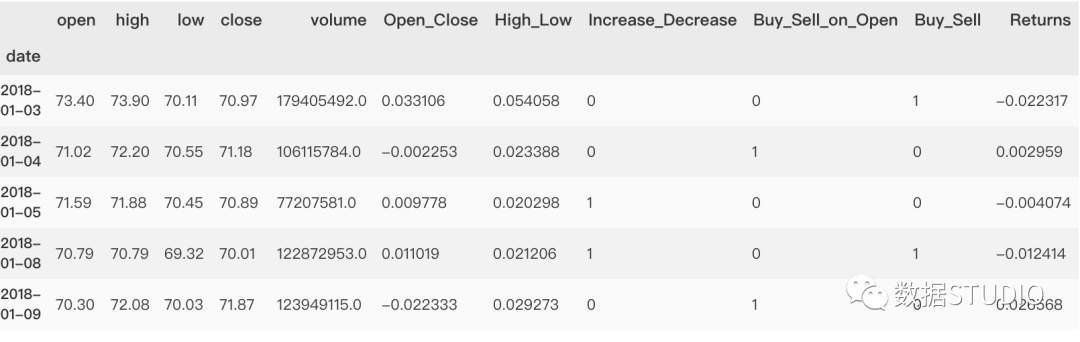
数据准备

本次分类分析使用股市数据。此处可参考金融数据准备。

KNN

K-Nearest Neighbors (KNN) 是一种懒惰学习算法和分类算法。此外，KNN是机器学习中最简单的方法。利用KNN进行分类，预测新点的分类。

数据预处理

从数据集

dataset

中选取需要用的数据作为输入数据和标签。

X = dataset.loc[ : , ['high','low','close']].values
y = dataset.loc[ : , ['Up_Down']].values

from sklearn.model_selection import train_test_split  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)  

数据标准化

数据标准化对于距离类模型，数据归一化是非常有必要的。这里使用

sklearn.preprocessing

中

StandardScaler

。

from sklearn.preprocessing import StandardScaler  
scaler = StandardScaler()  
scaler.fit(X_train)
X_train = scaler.transform(X_train)  
X_test = scaler.transform(X_test) 

模型训练与预测

from sklearn.neighbors import KNeighborsClassifier  
knn = KNeighborsClassifier(n_neighbors=5)  
knn.fit(X_train, y_train) 
y_pred = knn.predict(X_test)

模型评价

from sklearn.metrics import classification_report, confusion_matrix  
print(confusion_matrix(y_test, y_pred))  
print(classification_report(y_test, y_pred))

[[39 31]
 [32 44]]
              precision  recall  f1-score   support
          -1       0.55    0.56      0.55        70
           1       0.59    0.58      0.58        76
    accuracy                         0.57       146
   macro avg       0.57    0.57      0.57       146
weighted avg       0.57    0.57      0.57       146

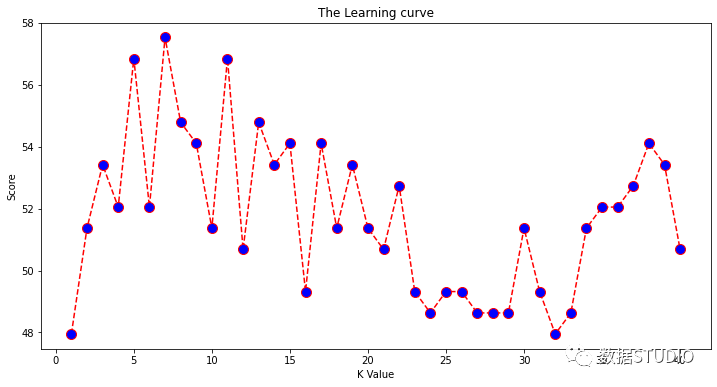
绘制学习曲线

分类以KNeighbors个数为x轴，模型得分为y轴，绘制学习曲线，以模型得分最高的n_neighbors为本次模型最终参数。

from sklearn.metrics import accuracy_score
score = []
for K in range(40):
    K_value = K+1
    knn = KNeighborsClassifier(n_neighbors = K_value, weights='uniform', algorithm='auto')
    knn.fit(X_train, y_train) 
    y_pred = knn.predict(X_test)
    score.append(round(accuracy_score(y_test,y_pred)*100,2))
    
plt.figure(figsize=(12, 6))  
plt.plot(range(1, 41), score, color='red', linestyle='dashed', marker='o',  
         markerfacecolor='blue', markersize=10)
plt.title('The Learning curve')  
plt.xlabel('K Value')  
plt.ylabel('Score') 

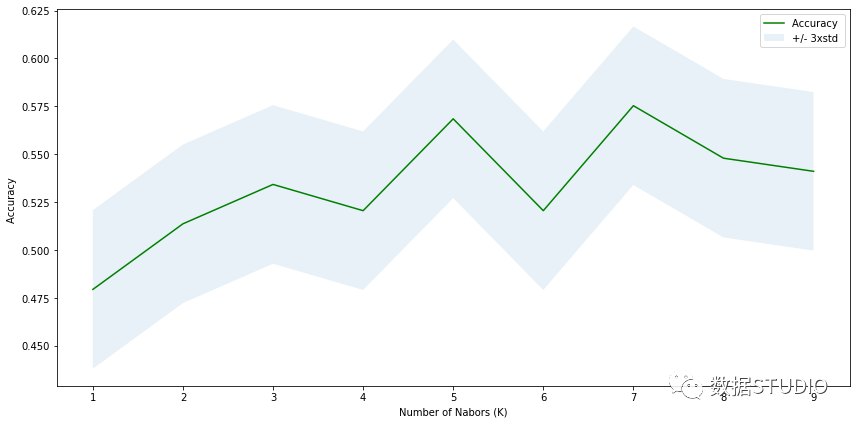
带误差线的学习曲线

from sklearn import metrics
Ks = 10
mean_acc = np.zeros((Ks-1))
std_acc = np.zeros((Ks-1))
ConfustionMx = [];
for n in range(1,Ks):
    
    # 模型训练和预测
    neigh = KNeighborsClassifier(n_neighbors = n).fit(X_train,y_train)
    yhat=neigh.predict(X_test)
    mean_acc[n-1] = metrics.accuracy_score(y_test, yhat)
    std_acc[n-1]=np.std(yhat==y_test)/np.sqrt(yhat.shape[0])

# 绘图
plt.figure(figsize=(12,6))
plt.plot(range(1,Ks),mean_acc,'g')
plt.fill_between(range(1,Ks),mean_acc - 1 * std_acc,mean_acc + 1 * std_acc, alpha=0.10)
plt.legend(('Accuracy ', '+/- 3xstd'))
plt.ylabel('Accuracy ')
plt.xlabel('Number of Nabors (K)')
plt.tight_layout()
plt.show()
# print( "The best accuracy was with", 
          mean_acc.max(), "with k=", 
          mean_acc.argmax()+1) 

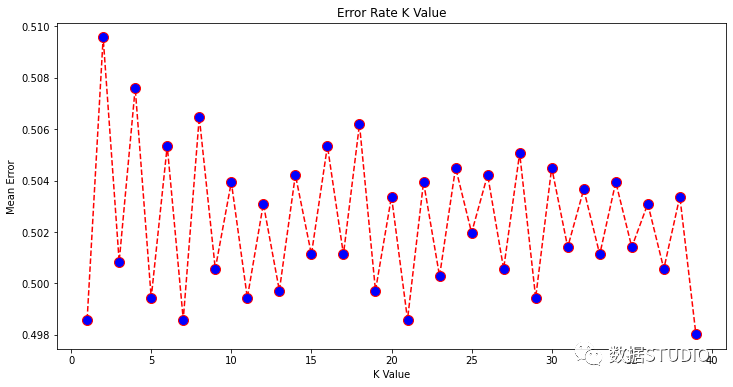
误差率可视化

error = []

# 计算K值在1-40之间多误差值
for i in range(1, 40):  
    knn = KNeighborsClassifier(n_neighbors=i)
    knn.fit(X_train, y_train)
    pred_i = knn.predict(X_test)
    error.append(np.mean(pred_i != y_test))
plt.figure(figsize=(12, 6))  
plt.plot(range(1, 40), error, color='red', linestyle='dashed', marker='o',  
         markerfacecolor='blue', markersize=10)
plt.title('Error Rate K Value')  
plt.xlabel('K Value')  
plt.ylabel('Mean Error')  

逻辑回归

逻辑回归是线性分类起，其本质是由线性回归通过一定的数学变化而来的。要理解逻辑回归，得先理解线性回归。线性回归是构造一个预测函数来映射输入的特性矩阵和标签的线性关系。线性回归使用最佳的拟合直线（也就是回归线）在因变量（）和一个或多个自变量（）之间建立一种关系。在这种技术中，因变量是连续的，自变量可以是连续的也可以是离散的，回归线的性质是线性的。

类比线性方程 ：

可以用矩阵的形式表示该方程，其中 x 与 w 均可以被看作一个列矩阵：

通过函数 ，线性回归使用输入的特征矩阵 来输出一组连续型的标签值

y_pred

，以完成各种预测连续型变量的任务。若标签是离散型变量，尤其是满足0-1分布的离散型变量，则可以通过引入联系函数(link function)，将线性回归方程 变换为 ，并且令 的值分布在 (0,1) 之间，且当 接近0时样本的标签为类别0，当 接近1时样本的标签为类别1，这样就得到了一个分类模型。而这个联系函数对于逻辑回归来说，就是

Sigmoid

函数

线性回归中 带入到

Sigmoid

函数中，即得到二元逻辑回归模型的一半形式：

其中 为逻辑回归的返回的标签值。假设已经训练好一组权值向量 。只要把我们需要预测的特征矩阵 带入到 方差中，得到输出值就是标签为类别1的概率，于是就能判断输入特征矩阵是属于哪个类别。

因此逻辑回归是不直接预测标签值，而是去预测标签为类别1的概率。一般地如果标签为类别1的概率大于0.5，就认为其为类别1，否在为类别2。

数据准备

定义x、y，数据标准化、划分训练集和测试集。

dataset['Buy_Sell'] = dataset['Buy_Sell'].astype('int')
X = np.asarray(dataset[['open', 'high', 'low', 'close', 'volume']])
y = np.asarray(dataset['Buy_Sell'])
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)

模型实例化

# 模型训练
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
LR = LogisticRegression(C=0.01, solver='liblinear').fit(X_train,y_train)
yhat = LR.predict(X_test)

# predict_proba是所有类的估计值的返回，按类的标签排序。
# 第1列是第1类P(Y=1|X)的概率，第二列是第0类P(Y=0|X)的概率

yhat_prob = LR.predict_proba(X_test)

模型评价

jaccard_score

雅卡尔指数（Jaccard index），又称为雅卡尔相似系数（Jaccard similarity coefficient），是用于比较样本集的相似性与多样性的统计量。雅卡尔系数能够量度有限样本集合的相似度，其定义为两个集合交集大小与并集大小之间的比例：

from sklearn.metrics import jaccard_score
jaccard_score(y_test, yhat)

混淆矩阵

from sklearn.metrics import classification_report, confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
                          normalize=False,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    This function prints and plots the confusion matrix.
    Normalization can be applied by setting `normalize=True`.
    """
    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
        print("Normalized confusion matrix")
    else:
        print('Confusion matrix, without normalization')
    print(cm)

    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=45)
    plt.yticks(tick_marks, classes)

    fmt = '.2f' if normalize else 'd'
    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, format(cm[i, j], fmt),
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

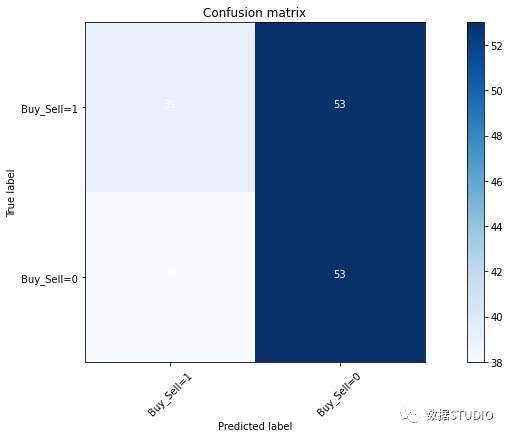
计算混淆矩阵并绘制非标准化混淆矩阵

cnf_matrix = confusion_matrix(y_test, yhat, labels=[1,0])
np.set_printoptions(precision=2)
plt.figure(figsize=(12,6))
plot_confusion_matrix(cnf_matrix, 
                      classes=['Buy_Sell=1','Buy_Sell=0'],
                      normalize= False,  
                      title='Confusion matrix')

Confusion matrix, without normalization
[[39 53]
 [38 53]]

分类模型评价报告

print (classification_report(y_test, yhat))

            precision   recall  f1-score   support
           0     0.50   0.58      0.54        91
           1     0.51   0.42      0.46        92
    accuracy                      0.50       183
   macro avg     0.50   0.50      0.50       183
weighted avg     0.50   0.50      0.50       183

对数损失

对数损失(对数损失)度量预测输出为0到1之间的概率值的分类器的性能。

from sklearn.metrics import log_loss
log_loss(y_test, yhat_prob)
>>> 0.690790520605071
LR2 = LogisticRegression(C=0.01, solver='sag').fit(X_train,y_train)
yhat_prob2 = LR2.predict_proba(X_test)
print ("LogLoss: : %.2f" % log_loss(y_test, yhat_prob2))
LogLoss: : 0.69

ROC

Receiver Operating Characteristic(ROC) 曲线显示了一种检测或一种检测组合的每一个可能截止点的敏感性和特异性之间的联系/权衡。此外，该曲线是比较两个工作特征真阳性率(TPR)和假阳性率(FPR)。曲线下面积(Area Under Curve, AUC)是代表二值分类的ROC曲线下的面积。

y_pred_proba = LR.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test,  y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)
plt.figure(figsize=(12,6))
plt.plot(fpr,tpr,label="data 1, auc="+str(auc))
plt.legend(loc=4)
plt.show()

朴素贝叶斯分类器

朴素贝叶斯分类器是一种基于概率统计的分类方法，在条件独立假设的基础上使用贝叶斯定理构建算法，能够通过提供后验概率估计来量化预测中的不确定性的概率分布模型。

一些特点

• 把目标类视为能导致数据实例生产的因素，朴素贝叶斯分类器也是生成类模型。
• 使用朴素贝叶斯假设，即使在给定类别标签的条件下，属性也可以很容易地计算高维设置中的类条件概率，常用与文本分类。
• 对孤立噪声和不相关属性具有鲁棒性。
• 通过计算其条件概率估计时忽略每个属性的缺失值，来处理训练集的缺失值。
• 相关属性会降低其性能。

贝叶斯定理

贝叶斯定理给出了条件概率 与 之间的关系。

• 目标类的后验概率 是给定属性 的数据实例中观察到类别标签 的概率。
• 给定类别的属性的类条件概率，测量从属于 类的实例分布中观察到 的可能性。
• 先验概率 独立于观察到的属性值。先验概率捕获了关于类别分布的先验知识。

朴素贝叶斯假设所有属性 的类条件概率可以被分解为类条件概率的乘积：(给定类别标签 ，属性 是相互独立的)

由于对于每个都是一样的，所以朴素贝叶斯方程：

在小数据集上仍然可以使用先验概率作为后验概率的估计，通过不断增加更多的属性，可以不断细化后验概率。

求解步骤

• 拟合和 , 拟合的方法就是直接从样本计算对应频率；
• 由得出联合概率分布。
• 由得出后验概率，通过后验概率进行分类。

算法实现

X = dataset[['open', 'high', 'low', 'volume', 'close','Returns']].values
y = dataset['Buy_Sell'].values

from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix

model = GaussianNB()
sss = StratifiedShuffleSplit(n_splits=5, test_size=0.50, random_state=None)
sss.get_n_splits(X, y)

cm_sum = np.zeros((2,2))

for train_index, test_index in sss.split(X, y):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)
    cm = confusion_matrix(y_test, y_pred)
    cm_sum = cm_sum + cm
print('\nNaive Bayes Gaussian Algorithms')
print('\nConfusion Matrix')
print('_'*20)
print('     Predicted')
print('     pos neg')
print('pos: %i %i' % (cm_sum[1,1], cm_sum[0,1]))
print('neg: %i %i' % (cm_sum[1,1], cm_sum[0,1]))

Naive Bayes Gaussian Algorithms

Confusion Matrix
____________________
     Predicted
     pos neg
pos: 483 467
neg: 483 467

校准的预测概率

from sklearn.naive_bayes import GaussianNB
from sklearn.calibration import CalibratedClassifierCV
X = dataset.drop(['Buy_Sell'], axis=1).values
Y = dataset['Buy_Sell'].values
# 创建高斯朴素贝叶斯实例
clf = GaussianNB()
# 使用sigmoid校准创建校准交叉验证
clf_sigmoid = CalibratedClassifierCV(clf, cv=2, method='sigmoid')
# 校准的概率
clf_sigmoid.fit(X, Y)
"""
CalibratedClassifierCV(base_estimator=GaussianNB(priors=None, var_smoothing=1e-09),
            cv=2, method='sigmoid')
"""

# 创建新观察数据
new_observation = [[.4, .4, .4, .4, .4, .4, .4, .4, .4]]
clf_sigmoid.predict_proba(new_observation)
array([[0.50353248, 0.49646752]])
clf_sigmoid.score(X,Y)
0.49743589743589745

决策树分类器

决策树是一种树状结构，她的每一个叶子结点对应着一个分类，非叶子结点对应着在某个属性上的划分，根据样本在该属性上的不同取值降气划分成若干个子集。

基本原理

数模型通过递归切割的方法来寻找最佳分类标准，进而最终形成规则。分类树用基尼系数最小化准则，进行特征选择，生成二叉树。

决策树的学习算法包含

特征选择、决策树的生成、决策树的剪枝过程

。

特征选择

选择对训练数据具有分类能力的特征，特征选择的准则是信息增益、或信息增益比，特征选择是决定用哪个特征来划分特征空间。

• 决策树通过信息增益准则选择特征。因为信息增益大的具有更强的分类能力。
• 具体方法：对于训练数据集，计算每个特征的信息增益，比较大小，选择信息增益大的那个特征。

分类决策树的生成

通过计算信息增益、信息增益比、基尼系数作为特征选择准则，从根节点开始，递归地产生决策树。这相当于利用不纯度不断选取局部最优特征，或将训练集分割为能够基本分类正确的子集。

CATA分类树的生成

用基尼系数选择最优特征，同时决定该特征的最优二值切分点。计算每个特征对数据集的基尼指数。对于每个特征 ，对其可能取的每个值 ，将数据集切分成两部分，并计算基尼指数。选择基尼系数最小的特征以及其切分点作为最优特征和最优切分点。不断循环直至满足条件停止。

决策树的剪枝

通过极小化决策树整体的损失函数或代价函数来实现。用的是正则化极大似然估计进行模型选择。损失函数定义为模型拟合程度和模型复杂度求和 ——

剪枝策略：预剪枝、后剪枝

预剪枝

定义

：决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化能力的提升，则停止划分并将该结点标记为叶子结点。

优缺点

：降低过拟合风险，减少训练和测试时间开销。但"贪心"本质带来欠拟合风险。

后剪枝

定义

：先从训练集生产一颗完整的决策树，自底向上地对非叶子结点进行考察，若该结点对应的子树替换为叶子结点能够带来决策树泛化能力的提升，则将该子树替换为叶结点。

优缺点

：欠拟合风险小，泛化能力优于预剪枝。但训练时间比未剪枝和预剪枝的时间开销大得多。

CATA树的剪枝

第一步

：从生成的决策树 底部进行剪枝，直到根节点，形成一个子树序列 。

第二步

：利用交叉验证在验证集上对子树序列进行测试，选择最优子树。
决策树算法算法描述ID3算法其核心是在决策树的各级节点上，使用信息增益方法的选择标准，来帮助确定生产每个节点时所对应采用的合适属性，不能自动分箱，不能剪枝C4.5算法相对于ID3改进是使用信息增益率来选择节点属性。
克服ID3点不足： ID3只适用于离散的描述属性，C4.5可以处理连续和离散属性；可以剪枝CART算法通过构建树、修剪树、评估树来构建一个二叉树。
通过控制树的结构来控制模型
当终节点是连续变量是——回归树
当终节点是分类变量是——分类树

算法实现

sklearn中的决策树实例

from sklearn.model_selection import train_test_split  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)

from sklearn.tree import DecisionTreeClassifier  
classifier = DecisionTreeClassifier()  
classifier.fit(X_train, y_train)

y_pred = classifier.predict(X_test)

from sklearn.metrics import classification_report, confusion_matrix  
print(confusion_matrix(y_test, y_pred))  
print(classification_report(y_test, y_pred))  

[[68  6]
 [10 62]]
              precision    recall  f1-score   support

        Down       0.87      0.92      0.89        74
          Up       0.91      0.86      0.89        72

    accuracy                           0.89       146
   macro avg       0.89      0.89      0.89       146
weighted avg       0.89      0.89      0.89       146

模型评价

混淆矩阵

import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import metrics

cm_matrix = metrics.confusion_matrix(y_test, y_pred)
cm_matrix

class_names=[0,1] # name  of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
sns.heatmap(pd.DataFrame(cm_matrix), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')
plt.show()
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

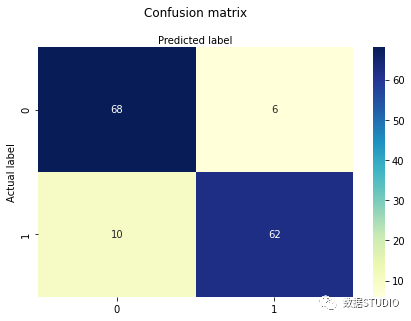
Accuracy: 0.8904109589041096

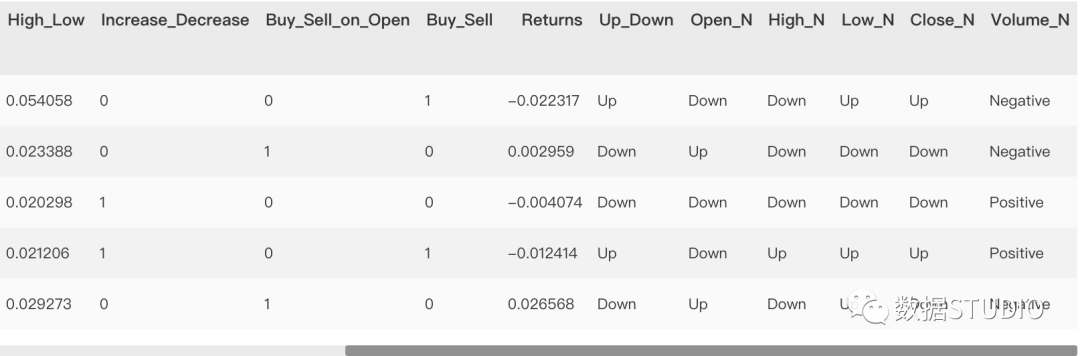
决策树用于特征创造

将每日来盘价、收盘价、交易量等进行环比，得到每天是增是减的分类型变量。

# 创造更多的时间
dataset['Open_N'] = np.where(dataset['open'].shift(-1) > dataset['open'],'Up','Down')
dataset['High_N'] = np.where(dataset['high'].shift(-1) > dataset['high'],'Up','Down')
dataset['Low_N'] = np.where(dataset['low'].shift(-1) > dataset['low'],'Up','Down')
dataset['Close_N'] = np.where(dataset['close'].shift(-1) > dataset['close'],'Up','Down')
dataset['Volume_N'] = np.where(dataset['volume'].shift(-1) > dataset['volume'],'Positive','Negative')
dataset.head()

数据预处理

X = dataset[['Open', 'Open_N', 'Volume_N']].values
y = dataset['Up_Down']

from sklearn import preprocessing
le_Open = preprocessing.LabelEncoder()
le_Open.fit(['Up','Down'])
X[:,1] = le_Open.transform(X[:,1]) 

le_Volume = preprocessing.LabelEncoder()
le_Volume.fit(['Positive', 'Negative'])
X[:,2] = le_Volume.transform(X[:,2]) 

from sklearn.model_selection import train_test_split  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)

模型建立与预测

from sklearn.tree import DecisionTreeClassifier  
classifier = DecisionTreeClassifier()  
classifier.fit(X_train, y_train)
# 实例化模型
Up_Down_Tree = DecisionTreeClassifier(criterion="entropy", max_depth = 4)
Up_Down_Tree
Up_Down_Tree.fit(X_train,y_train)
# 预测
predTree = Up_Down_Tree.predict(X_test)
print(predTree[0:5])
print(y_test[0:5])

['Up' 'Up' 'Up' 'Up' 'Down']
date
2019-12-31      Up
2019-12-25      Up
2018-01-11      Up
2020-08-21    Down
2019-11-20    Down
Name: Up_Down, dtype: object

决策树可视化

from sklearn.tree import DecisionTreeClassifier
from IPython.display import Image  
from sklearn import tree
# pip install pydotplus
import pydotplus
# 创建决策树实例
clf = DecisionTreeClassifier(random_state=0)
X = dataset.['open', 'high', 'low', 'volume', 'Open_Close', 'High_Low',
             'Increase_Decrease', 'Buy_Sell_on_Open', 'Returns']  
y = dataset['Buy_Sell'] 
# 训练模型
model = clf.fit(X, y)
# 创建 DOT data
dot_data = tree.export_graphviz(clf, out_file=None, 
                                feature_names=X.columns,  
                                class_names=X.columns)
# 绘图
graph = pydotplus.graph_from_dot_data(dot_data)  
# 展现图形
Image(graph.create_png())

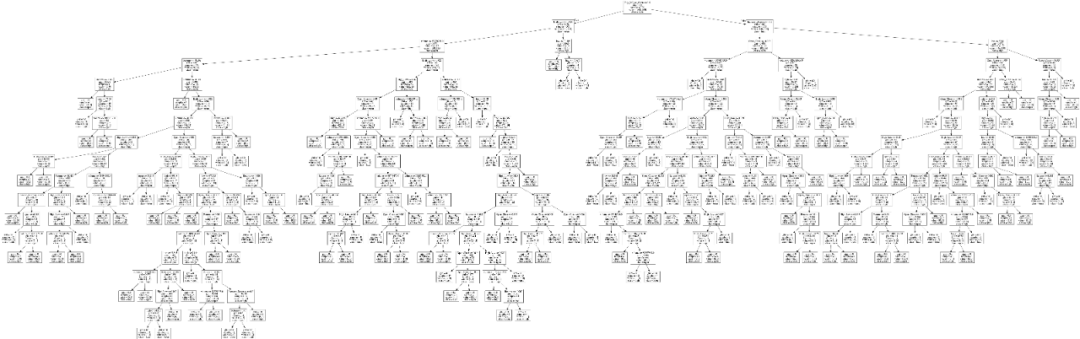
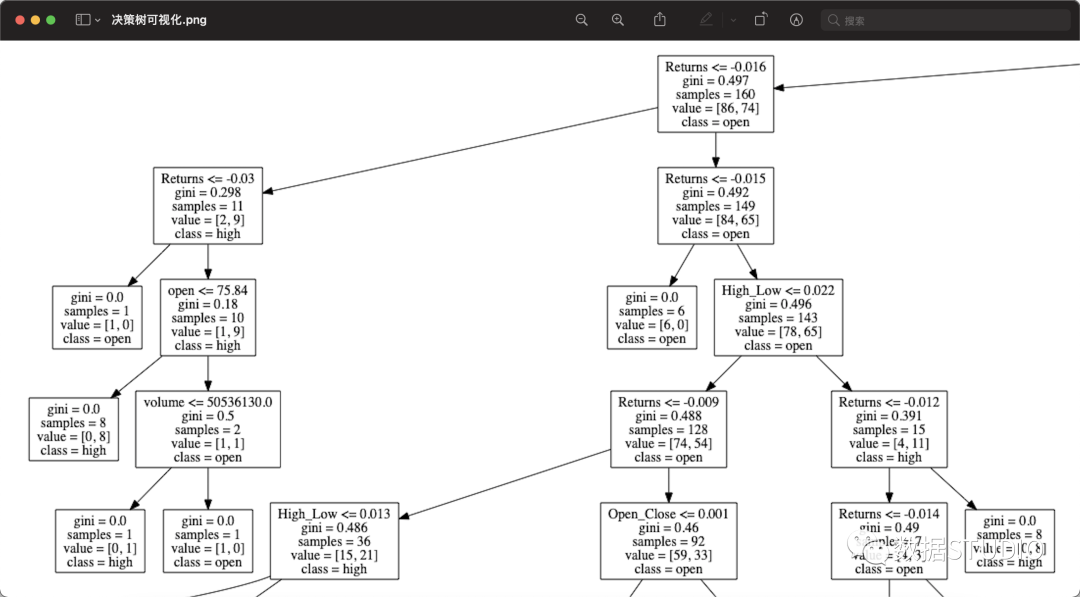
决策树可视化2

这里展示了整个决策树决策过程，这里看似很不清晰，但放大后，能看清每个小框框的内容：分类规则、基尼指数、样本数、类别标签等等详细内容。

支持向量机分类器

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；

SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

SVM还包括核技巧，这使它成为实质上的非线性分类器。

Sklearn中实现SVM也是比较方便。

from sklearn.svm import SVC # "Support Vector Classifier"
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
model = SVC(kernel = 'rbf', C = 1000,gamma=0.001)
model.fit(X_train, y_train)
svc_predictions = model.predict(X_test)
print("Accuracy of SVM using optimized parameters ", accuracy_score(y_test,svc_predictions)*100)
print("Report : ", classification_report(y_test,svc_predictions))
print("Score : ",model.score(X_test, y_test))

更多分类模型效果评价可参见该文中的评价指标。

以上文章来源于数据STUDIO ，作者云朵君。