图神经网络(GNN)代表了一类强大的深度神经网络架构。在一个日益互联的世界里,因为信息的联通性,大部分的信息可以被建模为图。例如,化合物中的原子是节点,它们之间的键是边。
图神经网络的美妙之处在于它们能够在不牺牲重要细节的情况下直接对图结构数据进行操作。这一点在处理复杂的数据集(如化合物)时尤为明显,GNN使我们能够充分利用底层图形表示的丰富性。通过这样做,GNN能够更全面地理解原子和键之间的关系,从而为更准确和深入的分析开辟途径。
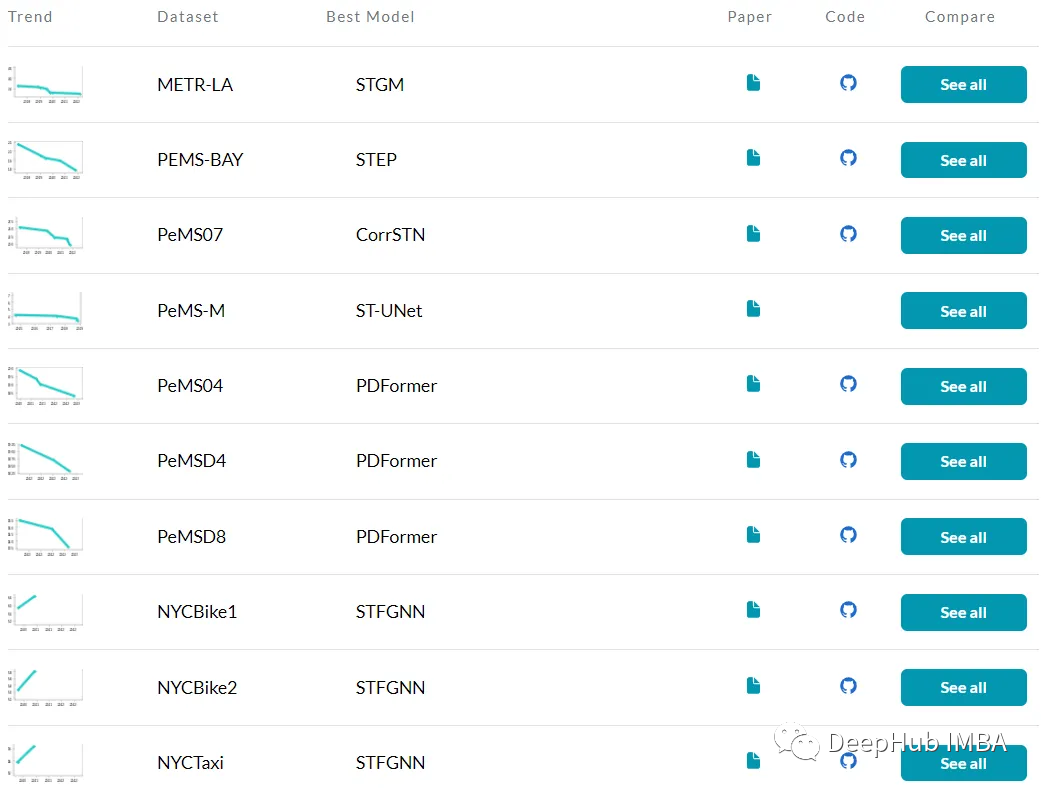
在化学领域之外,图结构的影响延伸到不同的领域。以交通数据为例,其中城市是节点,它们之间的路线是边。GNN在交通堵塞预测等任务中被证明是非常宝贵的,证明了它们在捕捉城市流动性的复杂动态方面是有效的。当面临预测交通拥堵等挑战时,GNN掌握图数据中固有的空间依赖性和模式的能力成为一种强有力的工具。基于GNN的众多模型已成为预测交通拥堵的最先进解决方案,成为最前沿的模型。下面是paperswithcode上预测交通堵塞的模型,基本上全部是GNN
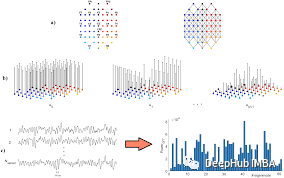
本文将介绍图卷积的理论基础。通过深入研究图傅立叶变换的复杂性及其与图卷积的联系,我们将为深入理解GNN世界中的这一关键概念奠定基础。
如何定义图卷积
GNN的核心概念在于图卷积,通过捕获节点和边之间的关系,实现对图数据的有效处理。
在理解图卷积的各种方法中,本文侧重于利用图傅里叶变换的理论来进行解释。这个概念提供了一个深入研究图卷积的机制的独特视角。
图傅里叶变换允许我们用图形频率来表示图形信号——与节点相关的数据。这种以光谱分析为基础的分解,提供了对图中潜在模式和结构的洞察。
一些GNN架构利用注意力机制和其他超越图卷积范围的高级方法。但是我们主要探讨图卷积的本质及其与图傅立叶变换的相互作用,所以注意力等部分不在本文的范围内
什么是图傅里叶变换?
图傅里叶变换的概念与经典的傅里叶变换有着有趣的相似之处。就像传统的傅里叶变换将一个波信号分解成它的组成频率一样,图傅里叶变换在图结构数据进行操作,揭示嵌入其中的信号的频率。
想象一个没有环路或多个边缘结构的加权无向图。图傅里叶变换是一种数学运算,它强调了图上存在的信号的变换。在信号维数等于1的情况下,这个概念变得特别具有说明性。考虑下面的描述,它描绘了信号在图表上的样子[1]。
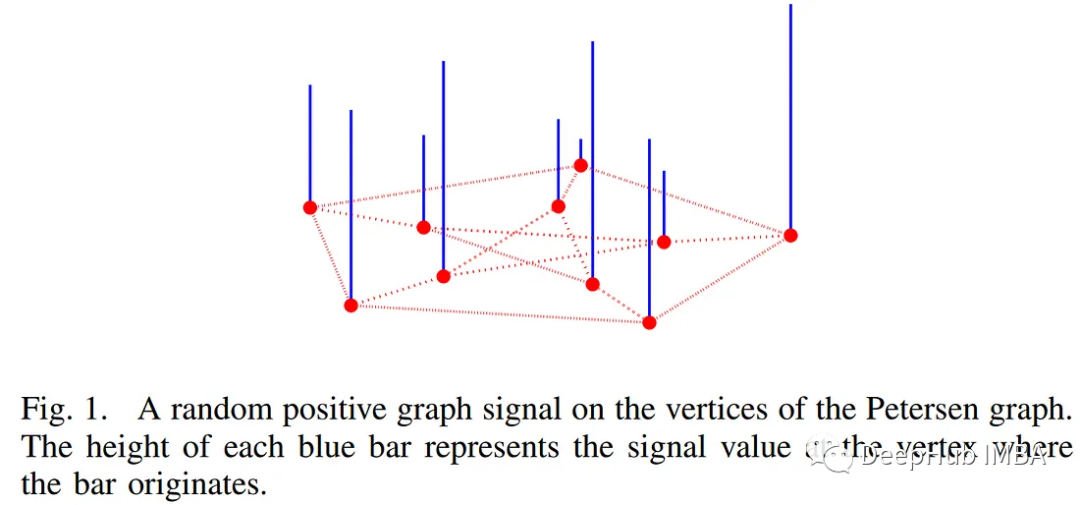
将信号分解为图的频率,或图傅里叶变换,提供了一种识别图形数据中固有的各种关系、规律和复杂性的方法。
图拉普拉斯算子
为了理解图的傅里叶变换,我们将开始一个基本的探索,首先介绍图的拉普拉斯变换。这个关键概念是揭示图形固有频率特性的基石。
图拉普拉斯量记为L,定义为:
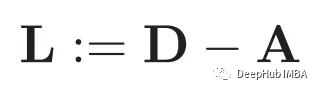
在这个等式中,A表示邻接矩阵,它编码了图中节点之间的连接,D表示度矩阵,捕获每个节点的度。
由于D和A是实对称矩阵,因此图拉普拉斯矩阵也具有实对称矩阵的性质。这个性质使我们能够对图拉普拉斯函数进行谱分解,表示为:

上式中,U表示特征向量矩阵,Λ是由特征值(Λ 1, Λ 2,…,Λ n)组成的对角矩阵。
二次形
本节解释了拉普拉斯图的二次形和二次形的含义,以及它如何与图信号的频率联系起来。
图拉普拉斯的二次型可以定义为:

这里的f表示图信号,w表示一条边的权值,Nk表示与节点k相连的节点集。
这个表示形式揭示了两个基本的关键方面:
函数的平滑性
二次型提供了对函数在图形上的平滑性的洞察。考虑f =[1,1,1,…,1]T的场景。根据图拉普拉斯式的定义,二次型的计算结果为零。也就是说,函数在节点间越平滑,得到的二次型就越小。这种相互作用提供了一种机制来量化图形信号固有的平滑程度。
相邻节点之间的相似性
二次型也用作评估相邻节点上信号之间相似性的度量。当f(i)与f(j)相差较大时,对应的二次型值成比例增大。相反,如果相邻节点上的信号相似,则二次型趋近于零。这种观察结果与二次型值越大反映相邻节点之间变化越大的想法是一致的。
有了这些概念,二次型就可以被解释为图形上函数“频率”的替代物。通过利用它提供信息,我们可以进行基于频率成分的图形信号分解。这一关键步骤是图傅里叶变换的先驱,解锁了一种强大的方法来揭示嵌入在图结构数据中的频率特征。
图傅里叶变换
我们已经建立了拉普拉斯图的二次形作为信号频率的指示器,其中二次形值越大表示频率越高。还有一个要点是:要注意这些值可能受到f的范数的影响。为了确保一致性并消除不同范数的潜在影响,我们还需要施加f的范数等于1的约束。
为了得到范数条件下二次型的平稳值,我们利用了拉格朗日乘子法这一强大的优化技术。对该问题进行适当的变换,最终得到一个特征值问题:

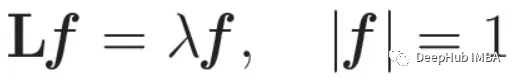
这个特征值提供了一个关系:L的每个特征值反映了图拉普拉斯的二次形的值。简单地说,这些特征值捕获了图形信号振动的频率。
这样我们对特征值作为函数频率的指标有了基本的理解。特征向量和图拉普拉斯之间的联系成为进行图傅立叶变换的途径——一个系统地揭示图信号内在频率元素的过程。
现在,我们可以看看傅里叶变换的定义了

从图傅里叶变换到图卷积
上面介绍的图傅里叶变换,我们获得了一个有效分析和处理图信号的强大工具。在我们研究图傅里叶变换和图卷积之间的联系。
这种联系的核心是卷积定理,这个原理建立了傅里叶域中卷积运算和元素积之间的联系。
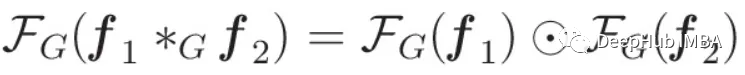
卷积运算类似于傅里叶域中变换后的信号的逐元乘法。利用卷积定理可以推导图卷积的一个间接定义:
- 对图形信号进行傅里叶变换。
- 将变换后的信号与一个可学习的权重向量相乘。
- 对元素积进行傅里叶反变换,得到图卷积的输出。
图卷积的公式现在可以表述如下:

为了使这个定义更加精简,我们引入了一个实用的参数化。由于与Uf的元素积可以表示为与diag(Uf)的积,s所以设可学习权值θ为:
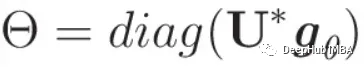
通过利用这种参数化,gθ的图卷积公式采用了一种简化和直观的形式:
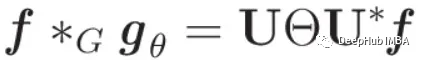
看看,我们已经从图的傅里叶变换中定义了一个图卷积!
总结
在本文中,我们从揭示图拉普拉斯的基本原理开始,然后深入研究了图卷积的基本概念,这是图傅里叶变换的推导。
本文中所做的推到应该能够加深了你对图卷积本质的理解。我们后续还会对图的消息传递机制进行更详细介绍,因为它可以聚合邻接节点信息,这是图卷积成功的关键。
引用:
[1] D. I. Shuman et al., “The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains”, IEEE Signal Processing Magazine, 30(3):83–98, 2013
作者:Lalf