【趣学算法】第一章 算法之美（上）

14天阅读挑战赛

【趣学算法】第一章 算法之美（上）

文章目录

1.打开算法之门

数据结构+算法=程序

数据结构是程序的骨架，算法是程序的灵魂。

2.妙不可言—算法复杂性

2.1 算法的引入

【算法的定义】

算法是对特定问题求解步骤的一种描述

【算法题】

写一个算法，求以下序列之和：

-1，1，-1,1，…,(-1)^n

以下是这道算法题的两种不同算法：

//算法1-1intsum1(int n){int sum=0;for(int i=1;i<=n;i++)
        sum+=pow(-1,i);//表示(-1)^ireturn sum;}

可以看出上面代码就是一个一个的老实算。吐槽一句：友友们，不是习惯从0开始吗？

//算法1-2intsum2(int n){int sum=0;if(n%2==0)
        sum=0;else
        sum=-1;}

算法1-2就聪明多了。

（额，我还以为第一个跟第二个加起来是0，第三个就开始-1所以看n的奇偶性。。。）

反正可以看出，算法1-1运行的次数比算法1-2多。

【“好”算法的标准】

（1）正确性

（2）易读性

（3）健壮性

（4）高效性（看时间复杂度）

（5）低存储性（看空间复杂度）

2.2 时间复杂度

【时间复杂度概念】

时间复杂度：算法运行需要的时间。

注意：不是以秒作为单位，而是执行的次数作为时间复杂度的衡量标准

【时间复杂度的求法】

//算法1-3int sum=0;//运行1次int total=0;//运行1次for(int i=1;i<=n;i++)//运行n+1次,最后一次判断不满足循环条件{
    sum=sum+i;//运行n次for(j=1;j<=n;j++)//运行n*(n+1)次{
        total=total+i*j;//运行n*n次}}

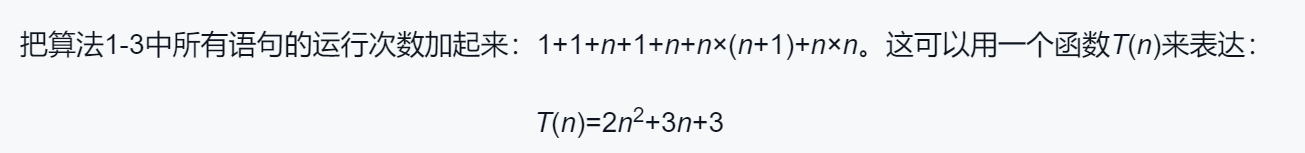
反正根据极限，得出结果：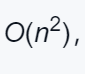

//算法1-4
i=1;//运行1次while(i<=n)//可假设可以执行x次{
    i=i*2;//可假设运行x次}

注意：不是所有算法都能直接计算运行次数

例如算法1-5，在数组a[n]中顺序查找x并返回其下标i。如果没有找到，则返回-1

//算法1-5 intfindx(int x){//在a[n]数组中顺序查找xfor(int i=0;i<n;i++){if(a[i]==x)return i;//查找成功，返回其下标i}return-1;//查找失败，返回-1 }

2.3 空间复杂度

【空间复杂度概念】

空间复杂度：算法占用的空间大小。

空间复杂度的本意是指算法在运行过程中占用了多少存储空间。算法占用的存储空间包括：

（1）输入、输出数据

（2）算法本身

（3）额外需要的辅助空间

输入/输出数据占用的空间是必需的，算法本身占用的空间可以通过精简算法来缩减，但缩减量是很小的，可以忽略不计。

算法在运行时所使用的辅助变量占用的空间（即辅助空间）才是衡量算法空间复杂度的关键因素。

这个辅助变量简而言之就是多开的变量。

【空间复杂度求法】

//算法1-6voidswap(int x,int y)//交换x与y{int temp;
    temp=x;//temp为辅助空间
    x=y;//(2)
    y=tmp;//(3)}

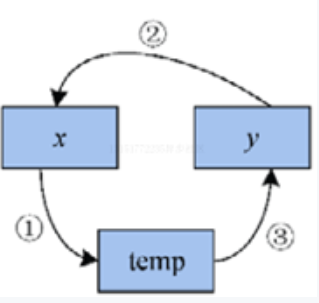
算法1-6使用了辅助空间temp，空间复杂度为O(1)。

//算法1-7 intfac(int n){//计算n的阶乘if(n==0||n==1)return1;elsereturn n*fac(n-1);}

注意：在递归算法中，每一次递推都需要一个栈空间来保存调用记录，因此在分析算法的空间复杂度时，需要计算递归栈的辅助空间。

阶乘是典型的递归调用问题，递归包括递推和回归。

递推是将原问题不断分解成子问题，直至满足结束条件，返回最近子问题的解；

然后逆向逐一回归，最终到达递推开始的原问题，返回原问题的解。

思考：试求5的阶乘，程序将怎样计算？

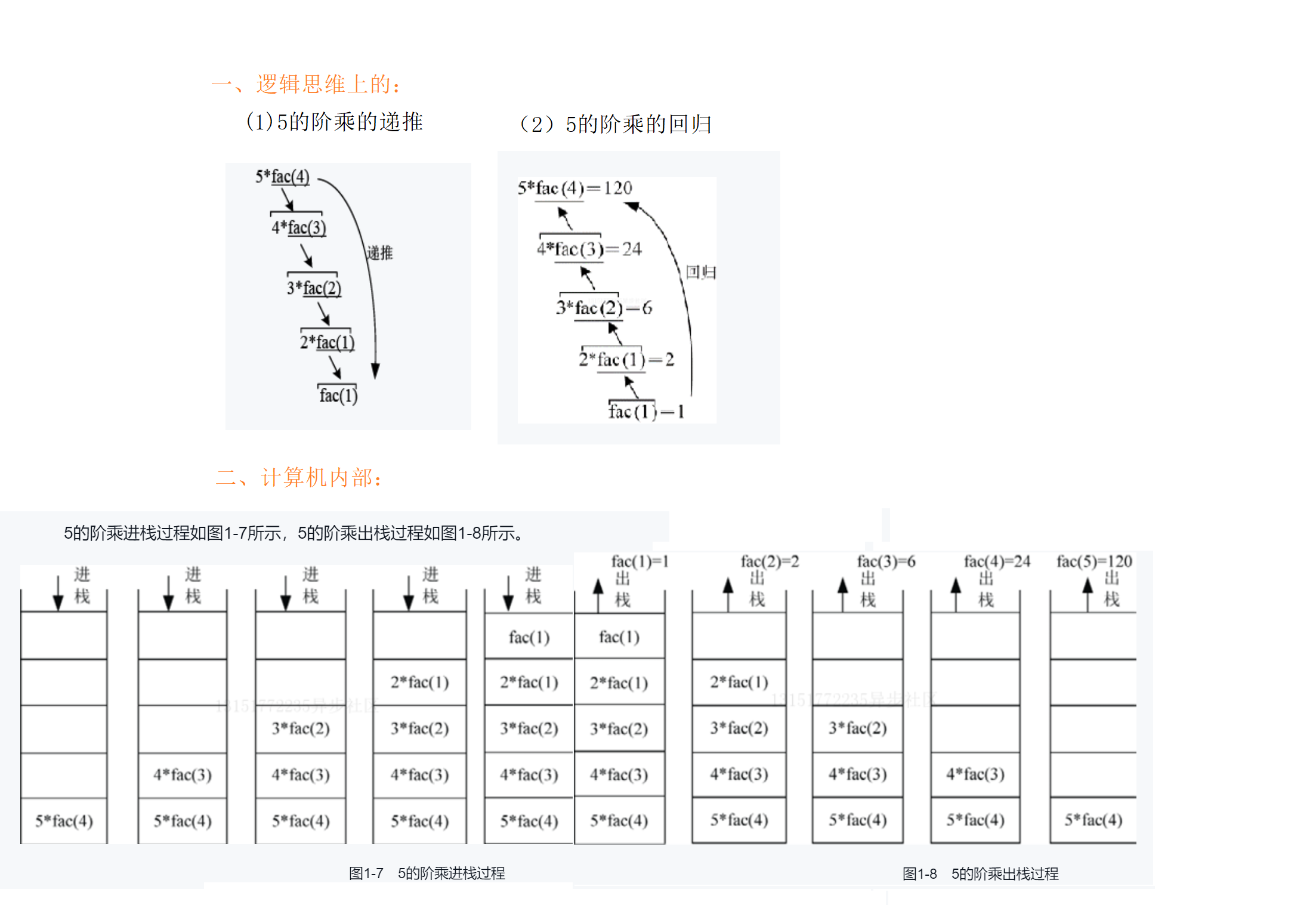
如果你栈不知道是什么，刚好，我写了篇博客：栈,点击跳转
完毕。