数学建模笔记（六）：常微分方程及其应用

文章目录

一、常微分方程概述

1.什么是常微分方程

前为数学摆方程，后为拉普拉斯方程

要确定每次积分后

     C 
    
   
  
    C 
   
  
C的值

2.以微分方程解决实际问题的一般思维

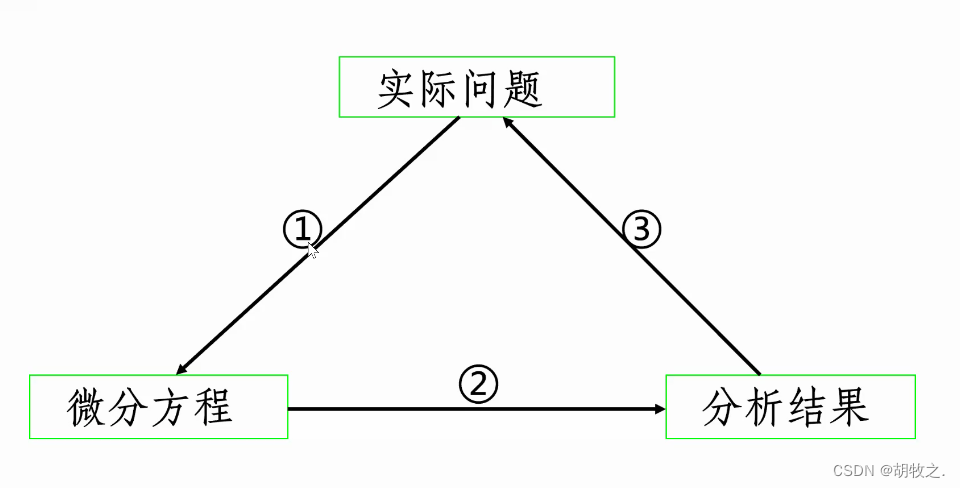
3.微分方程求解

4.微分方程适用问题

5.建立微分方程模型的方法

二、物体的冷却过程

1.问题背景

2.问题分析

3.模型建立与求解

三、水桶的放水过程

1.问题背景

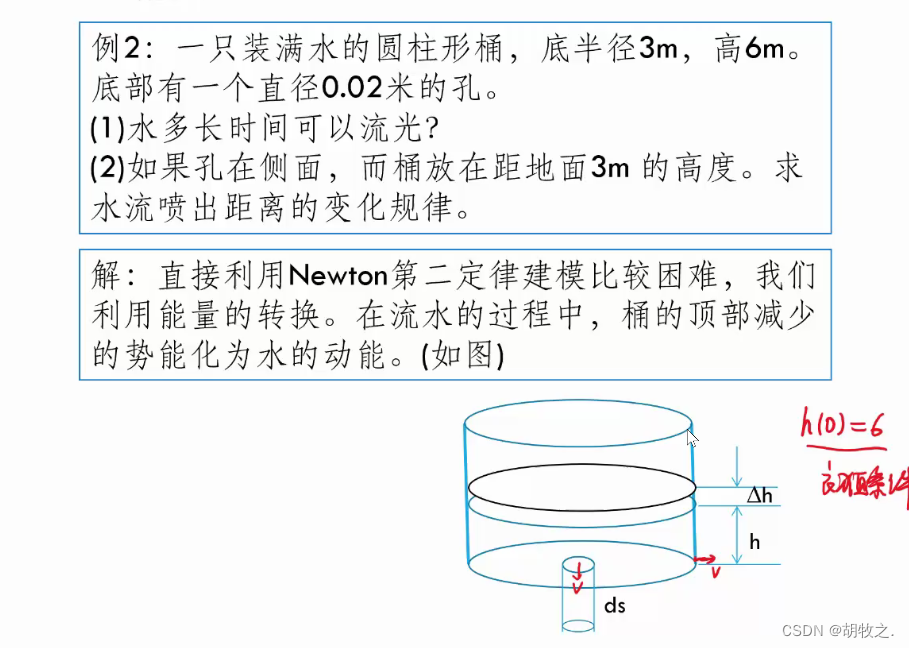
2.问题分析

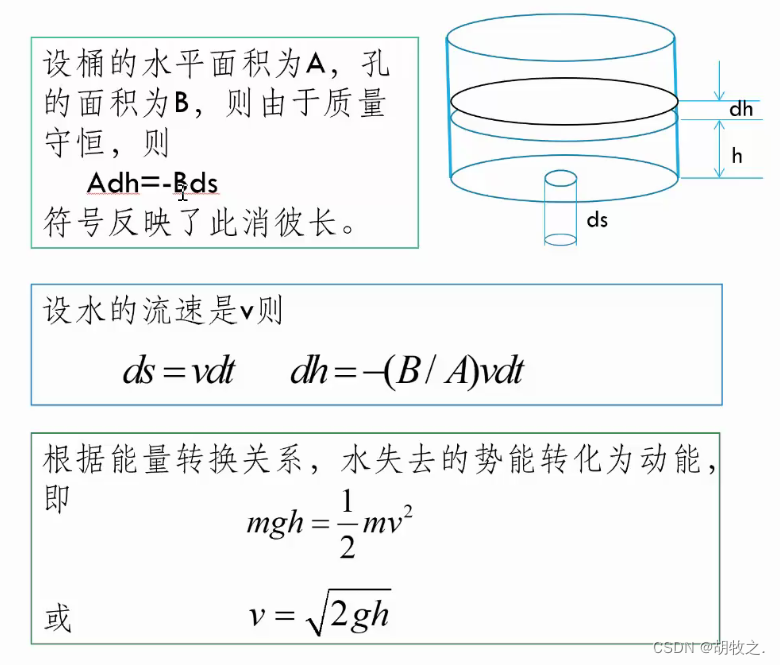
3.模型建立与求解

四、放射性废料的处理

1.问题背景

2.问题一模型建立

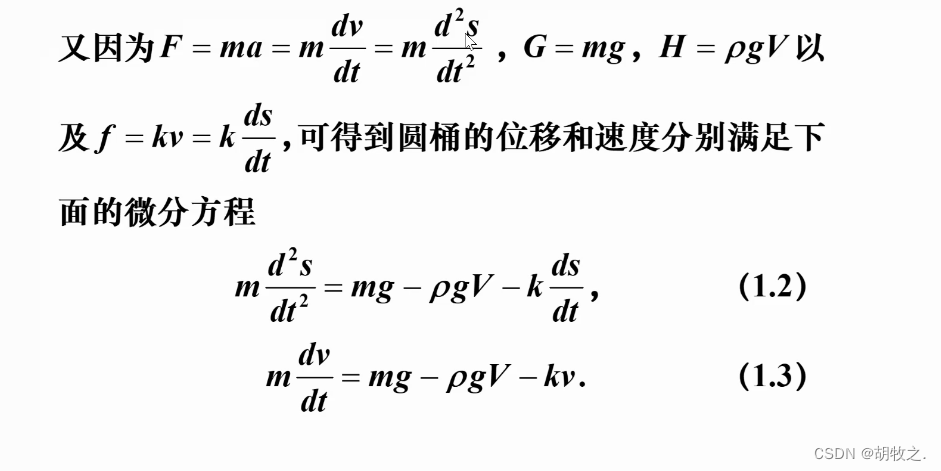
3.问题一模型求解

利用MATLAB求解

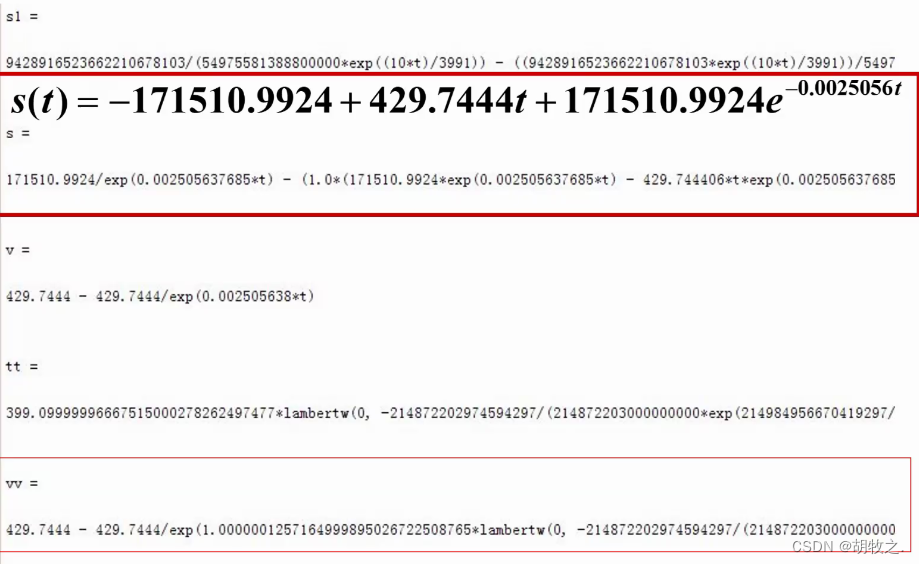
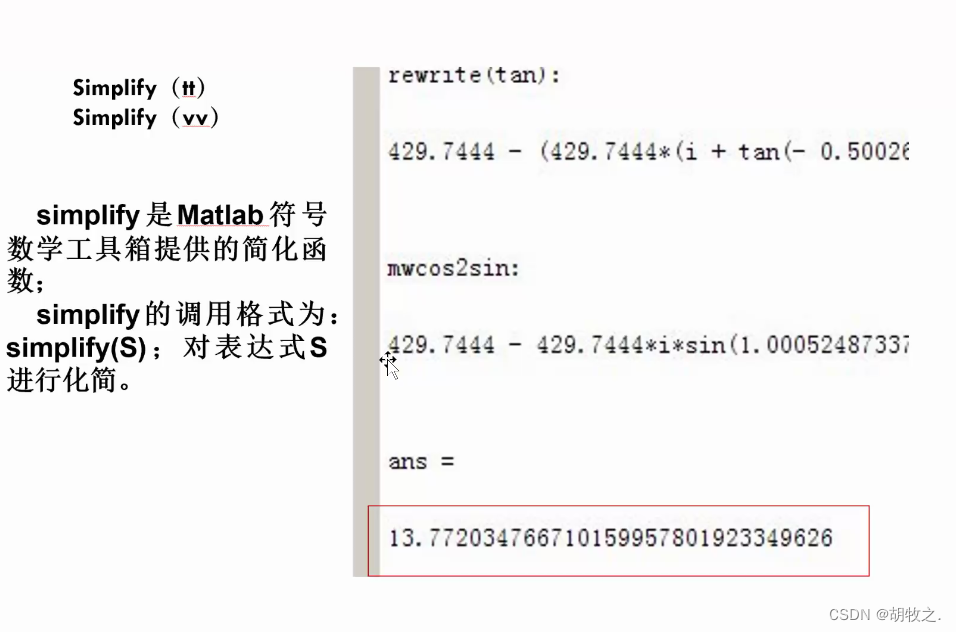
4.问题二模型建立

5.问题二模型求解

6.结果分析

五、预测人口的增长

1.问题背景

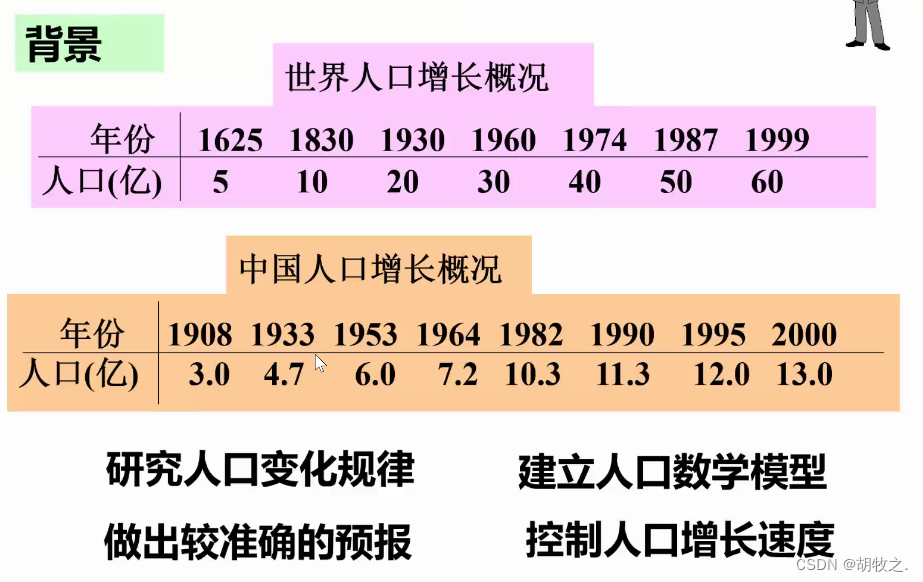
2.问题分析

3.模型求解

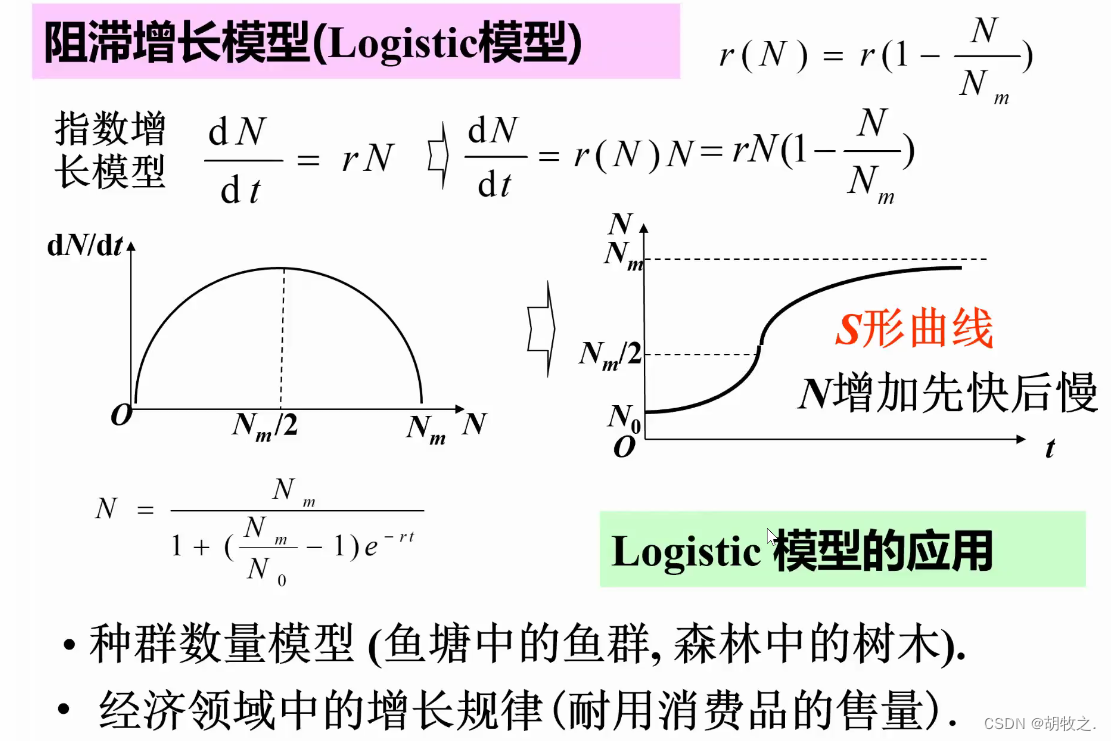
六、捕鱼业的持续收获

1.问题背景

2.问题分析

3.问题假设

4.模型建立

5.一阶常微分方程的平衡点及其稳定性

当

     t 
    
   
  
    t 
   
  
t趋于正无穷大时， 
 
  
   
   
     x 
    
   
     ( 
    
   
     t 
    
   
     ) 
    
   
  
    x(t) 
   
  
x(t)趋于 
 
  
   
    
    
      x 
     
    
      0 
     
    
   
  
    x_0 
   
  
x0​

使用泰勒展开，方程二为线性更易求解，使用变量分离法求解

6.模型求解

预测长时间后的情况

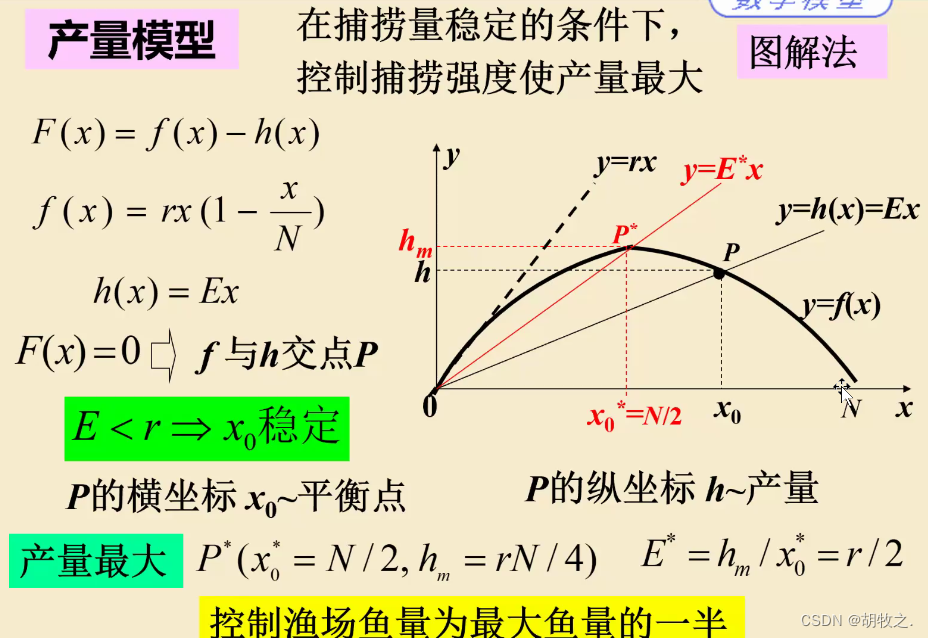
7.推广（效益模型）

效益最大点小于

      r 
     
    
      2 
     
    
   
  
    \frac{r}{2} 
   
  
2r​

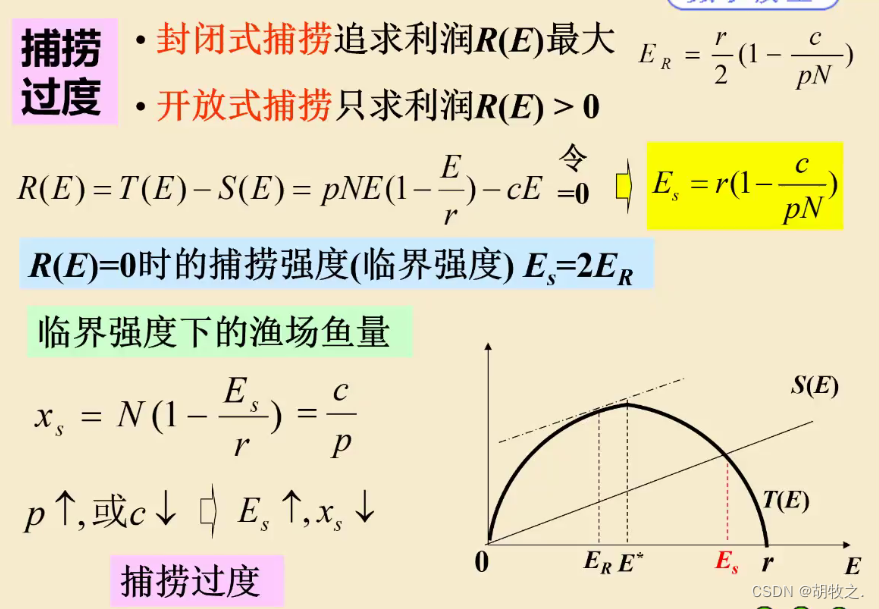
拿

      E 
     
     
     
       s 
      
     
       1 
      
     
    
   
  
    E_{s1} 
   
  
Es1​、 
 
  
   
    
    
      E 
     
     
     
       s 
      
     
       2 
      
     
    
   
  
    E_{s2} 
   
  
Es2​与 
 
  
   
    
    
      E 
     
    
      ∗ 
     
    
   
  
    E^{*} 
   
  
E∗比较

七、军备竞赛

1.问题背景

2.模型假设

3.模型建立

4.模型求解（线性常系数微分方程组的平衡点及其稳定性）

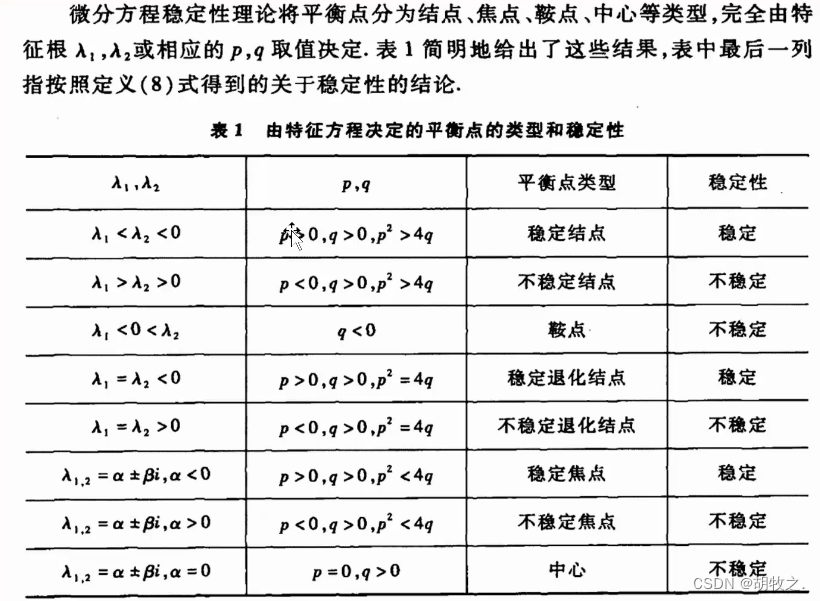
5.模型解释

八、种群的相互竞争

1.问题背景

2.模型假设

3.模型建立

4.模型求解

泰勒展开，近似


代入四个平衡点，求满足

     p 
    
   
     , 
    
   
     q 
    
   
  
    p,q 
   
  
p,q要求的平衡点

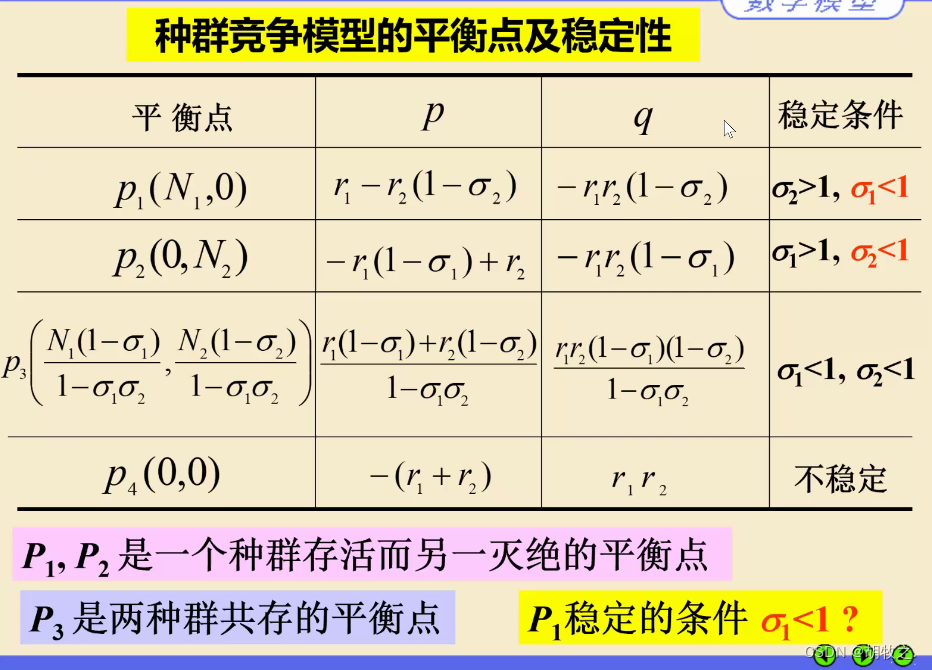
5.各个平衡点稳定性的相轨线分析

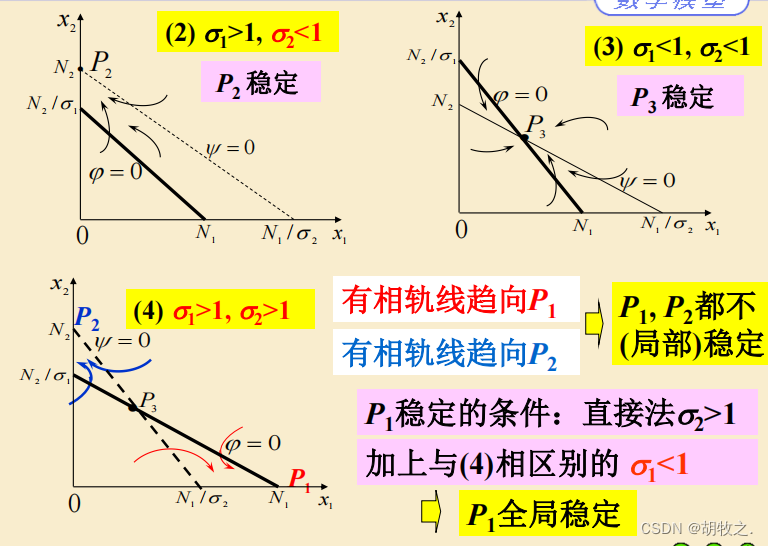
6.结果分析

理解为竞争能力，定性分析

九、种群的相互依存

1.问题背景

2.第一类类模型假设和建立

由于乙不能独立生存，所以在方程中为

     − 
    
   
     1 
    
   
  
    -1 
   
  
−1

3.第一类模型求解

要求

     p 
    
   
     q 
    
   
  
    pq 
   
  
pq都大于0

关于平衡点

      P 
     
    
      2 
     
    
   
  
    P_2 
   
  
P2​ 的相规线分析

由四个小区域

      s 
     
    
      1 
     
    
   
     , 
    
    
    
      s 
     
    
      2 
     
    
   
     , 
    
    
    
      s 
     
    
      3 
     
    
   
     , 
    
    
    
      s 
     
    
      4 
     
    
   
  
    s_1,s_2,s_3,s_4 
   
  
s1​,s2​,s3​,s4​，分析最终如何趋于平衡点

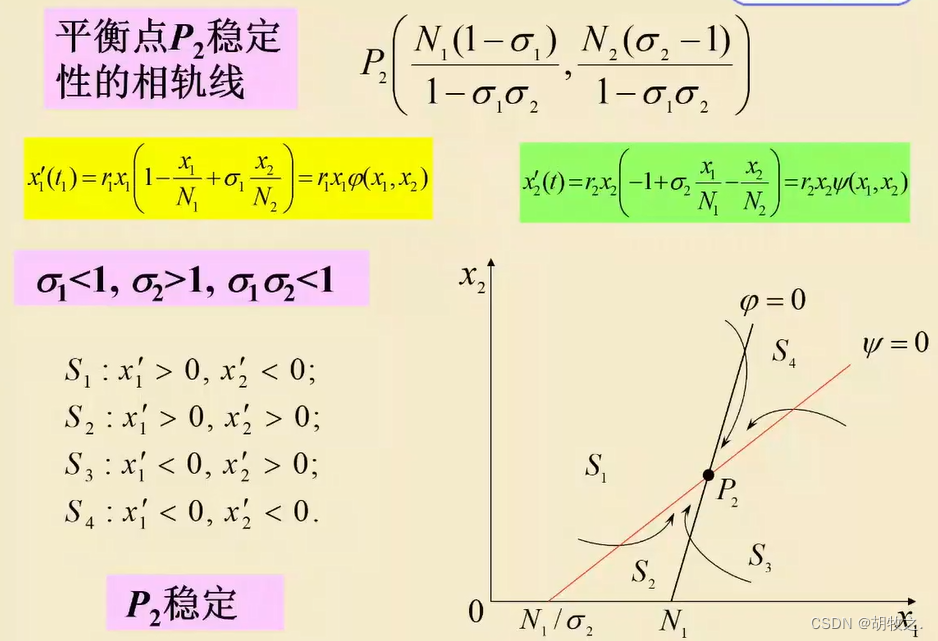
4.第一类结果分析

十、种群的弱肉强（食饵-捕食者模型）

1.问题背景

2.模型建立

3.模型求解

雅可比矩阵
雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此，雅可比矩阵类似于多元函数的导数




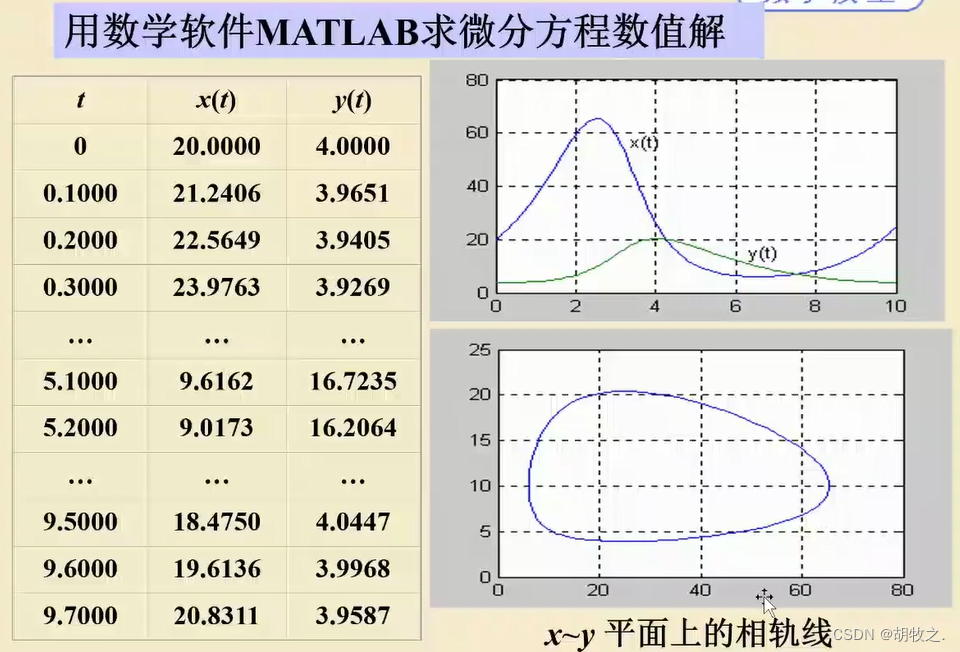
积分求解，先将原式

     x 
    
   
     ( 
    
   
     t 
    
   
     ) 
    
   
  
    x(t) 
   
  
x(t)替换，接下来就方便求积分

根据周期性，可知

     y 
    
   
     ( 
    
   
     T 
    
   
     ) 
    
   
     = 
    
   
     = 
    
   
     y 
    
   
     ( 
    
   
     0 
    
   
     ) 
    
   
  
    y(T)==y(0) 
   
  
y(T)==y(0)，所以相减结果为0

4.模型解释

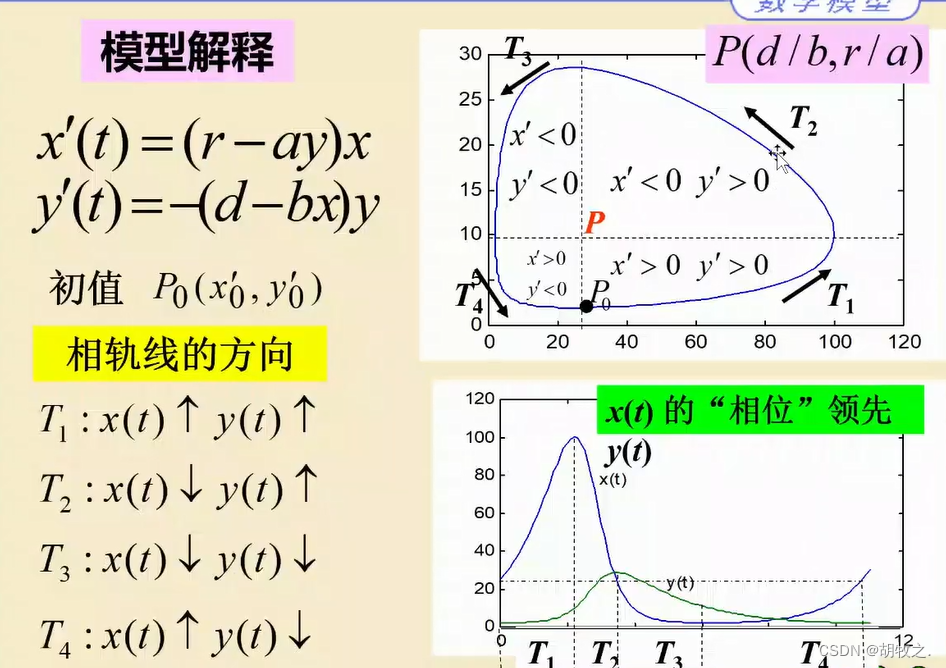
之前为自然情况的种群的发展，当有捕捞时，影响了食饵的自然增长率，捕食者的独立生存死亡率，种群的平均水平都有所下降；
战时捕捞，捕捞强度下降，种群平均水平有所回升；

5.模型的缺点与改进

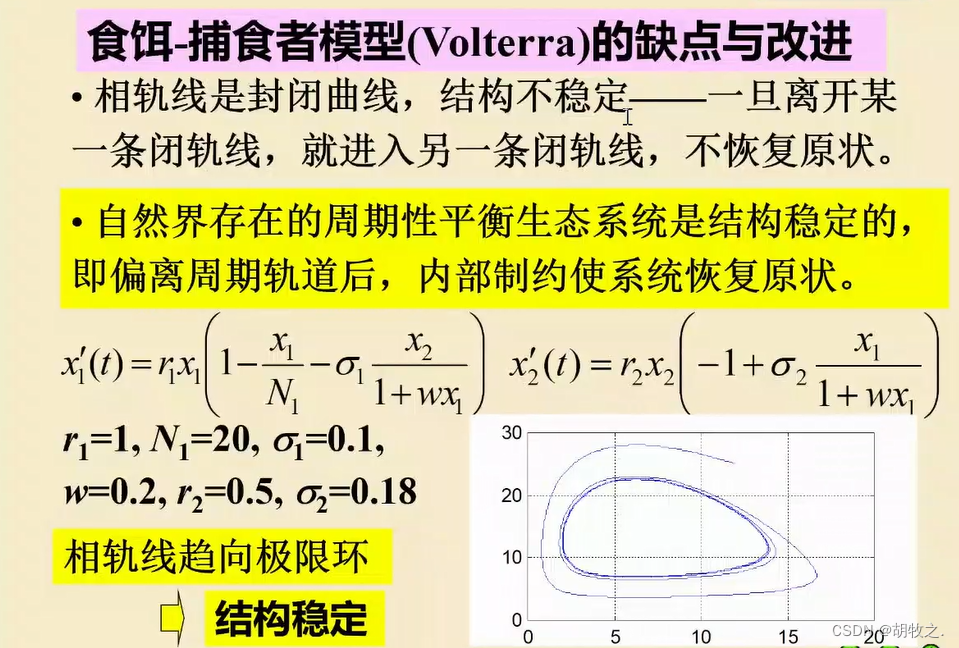
十一、药物中毒急救

1.问题背景

2.问题分析

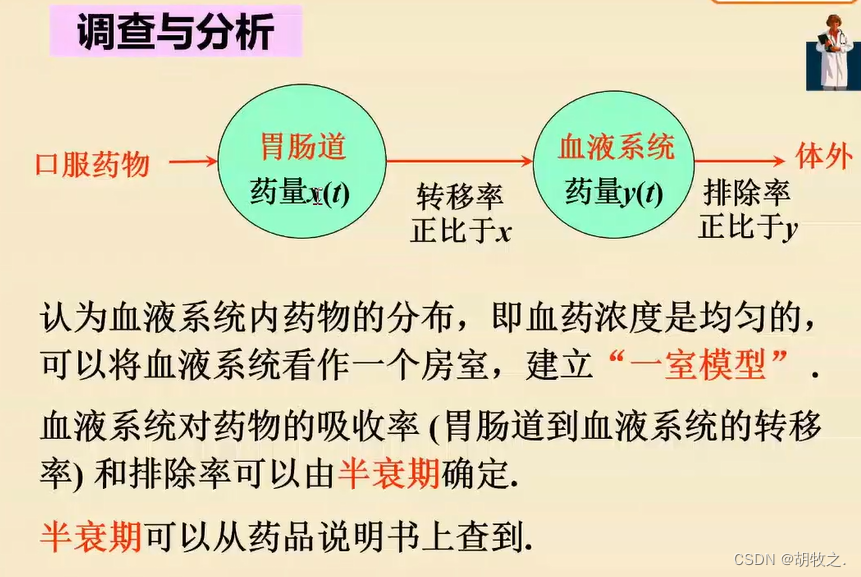
3.模型假设

半衰期是指血液中药物的浓度降低一半所需用的时间

4.模型建立

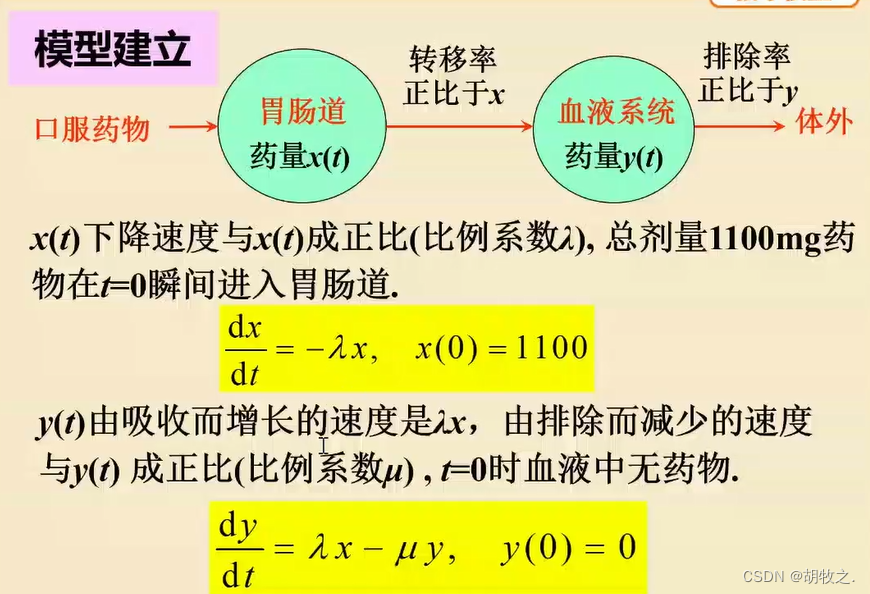
5.模型求解

变量分离
非齐次一阶线性微分方程，以常数变易求解

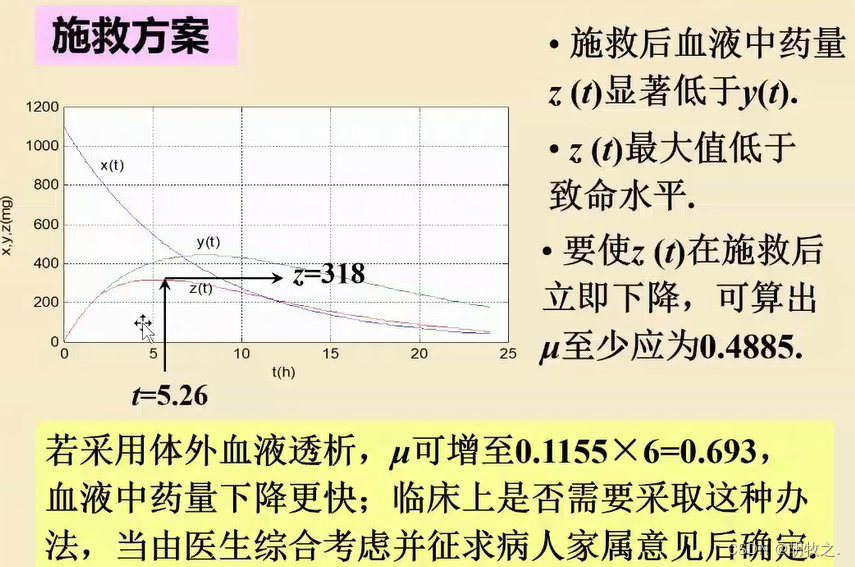
6.结果分析

假设血液总量为2000ml
根据临界药量算出临界时间，判断此时状况，再根据不同急救措施计算方程，讨论该采取何种措施；也可直接求出血药浓度立即所需要的最小排除率（也就是此时的导数为0）——原先的4.23倍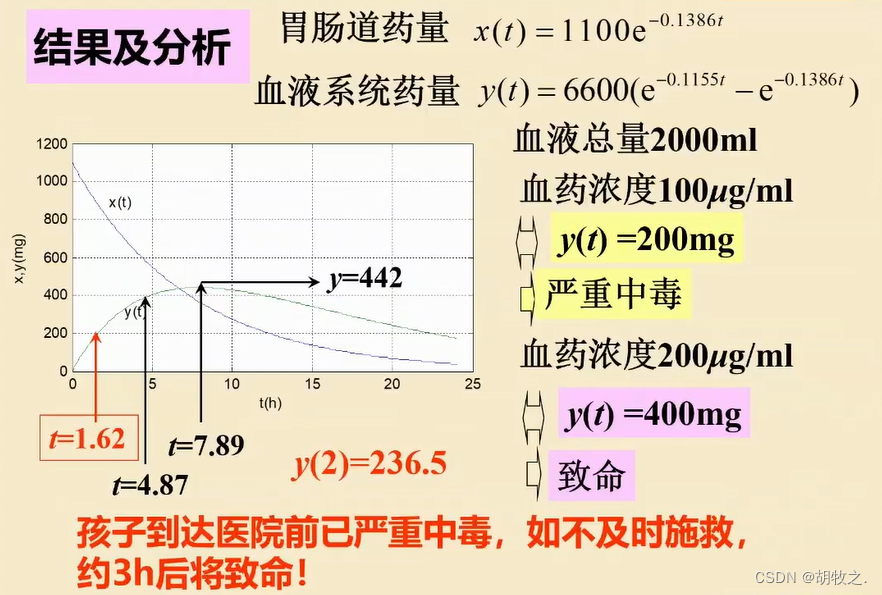

十二、人口增长（两种模型的参数估计）

1.问题背景

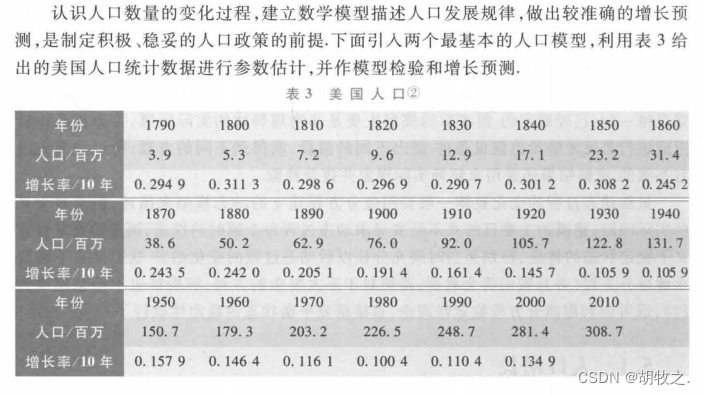
2.指数增长模型参数估计（数据拟合）——最小二乘法

3.指数增长模型参数估计（数据拟合）——数值微分

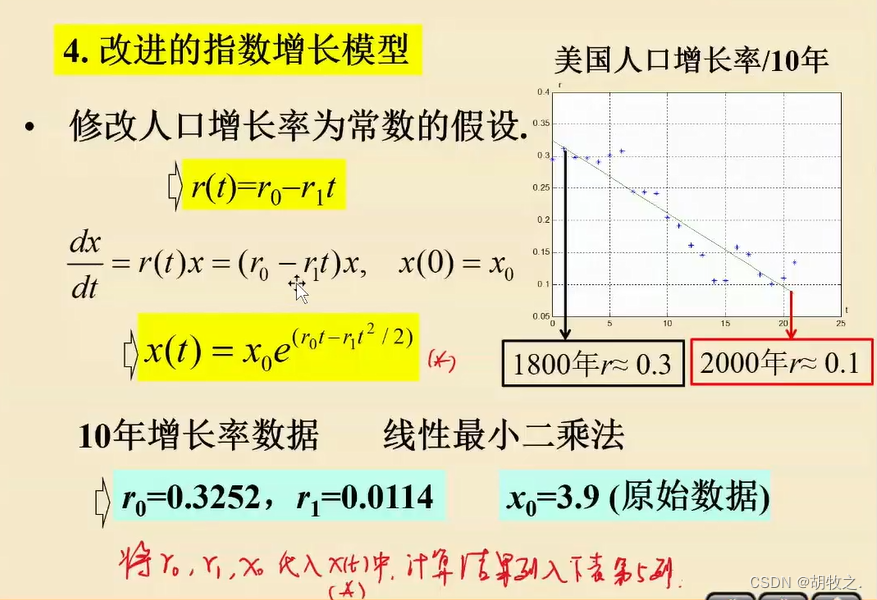
4.改进后的指数增长模型参数估计（数据拟合）——线性最小二乘法

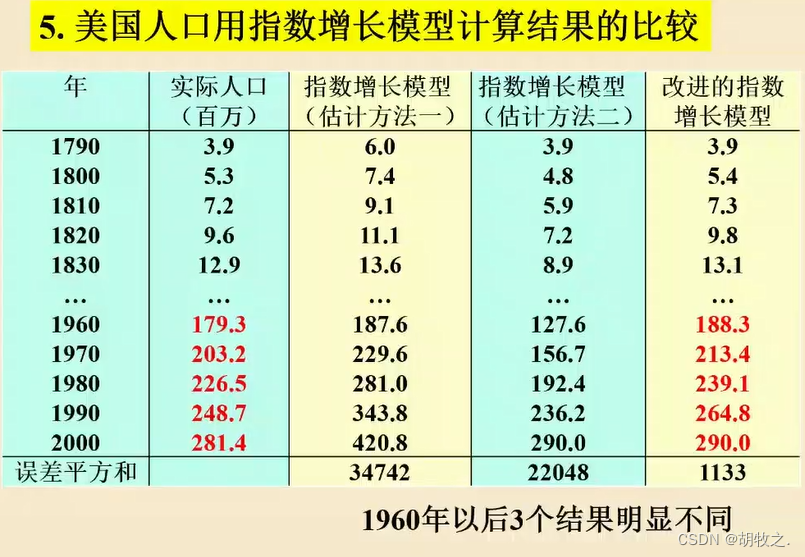
5.三类方法比较与结果分析

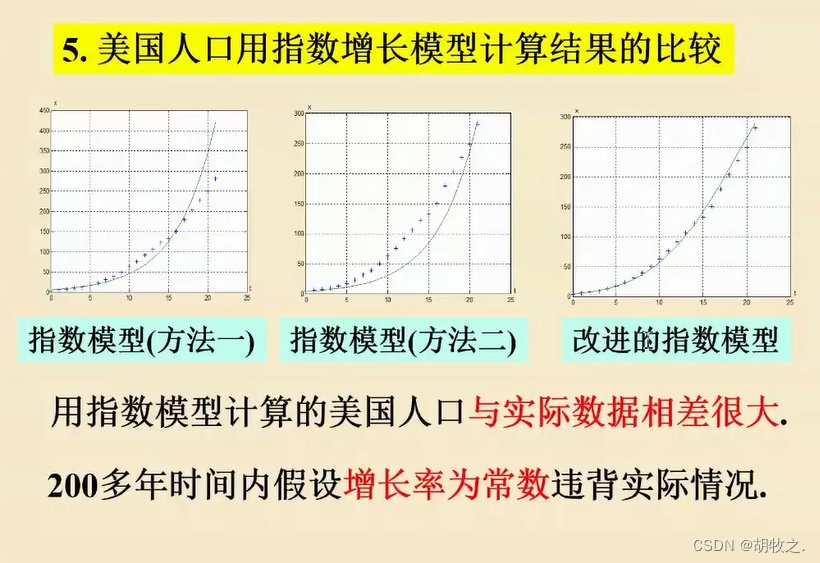
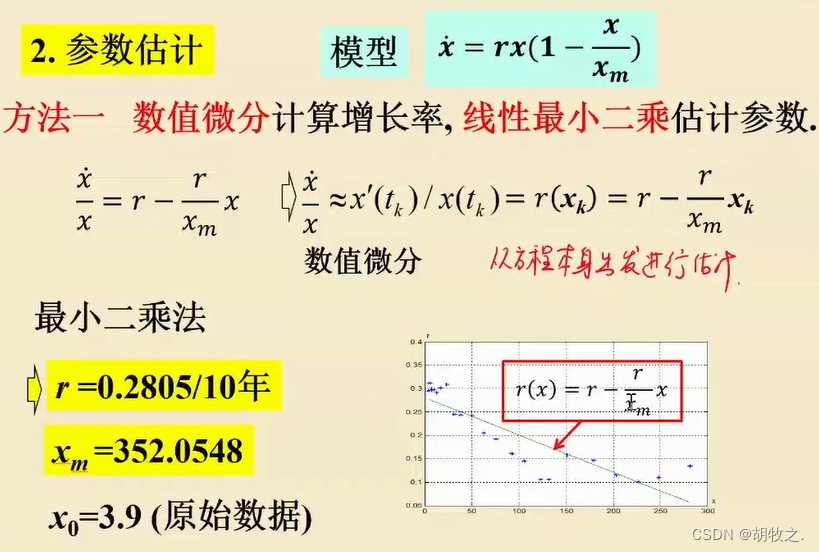
6.logistic模型——数值微分计算增长率，线性最小二乘估计参数

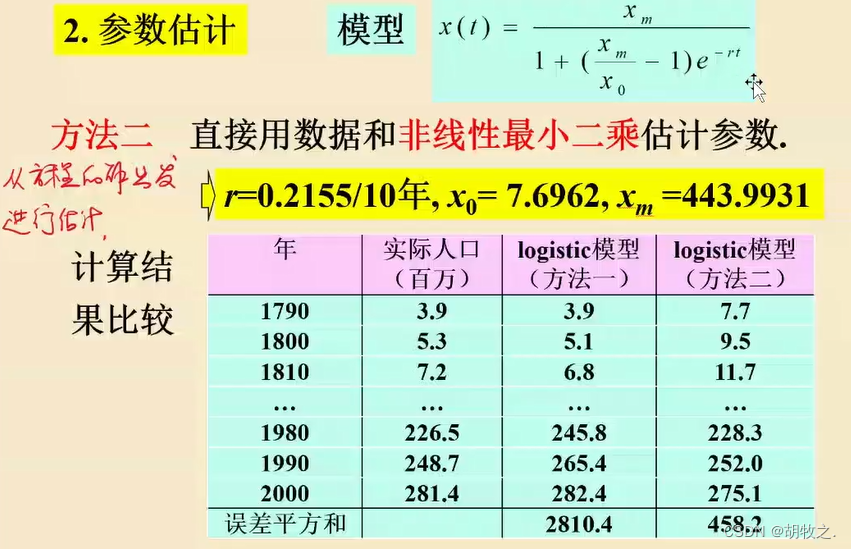
7.logistic模型——非线性最小二乘估计参数

从方程的解出发

8.两类方法比较与结果分析

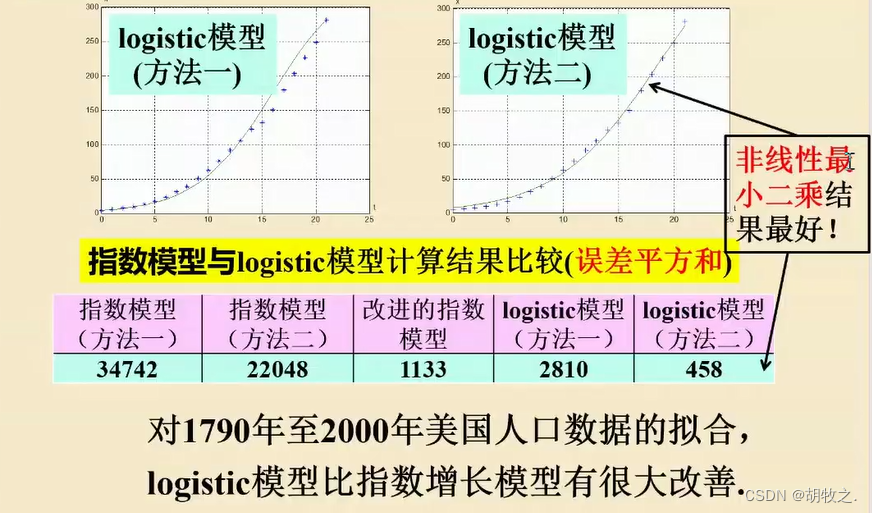
9.小结与批注