1 联邦学习提出的背景
在大多数情况下,数据分散的保存在各个企业手中,而各个企业希望在不公开自己数据的情况下,联合其他企业(利用各个企业所持有的数据)一起训练一个模型,该模型能够帮助企业获取更大的利益。
对于收集零散的数据,传统的方法是通过搭建一个数据中心,在数据中心对模型进行训练,但随着越来越多的法律限制加上数据拥有者不愿意透露自己的数据,这种方法已经渐渐行不通了。
2 联邦学习的介绍
定义:联邦学习(federated learning),全称联邦机器学习(federated machine learning),为了解决联合训练模型时的隐私问题,提出的一种方法:让各个企业自己进行模型的训练,各个企业在完成模型的训练之后,将各自模型的参数上传至一个中心服务器(也可以是点对点),中心服务器结合各个企业的参数(可以上传梯度,也可以是自己更新后的参数),重新拟定新的参数(例如通过加权平均,这一步叫做联邦聚合),将新的参数下发至各个企业,企业将新参数部署到模型上,从而继续新的训练,这个过程可以进行反复的迭代,直到模型收敛,或者满足其他的条件。![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-H8FpL0PN-1668479217904)(联邦学习(Federated Learning)].assets/image-20221114144201902.png)](https://img-blog.csdnimg.cn/4eb2a5b469f14705a5d4d2d80d20fcac.png)
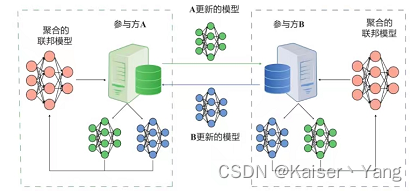
使用联邦学习模型的效果会比直接将数据集中起来进行训练要差,这样的效果损失(但实际情况下可能并没有损失,数据丢失可能类似于做了正则,效果可能反而会提升)换取了隐私的保护,是可以接受的。
3 联邦学习的分类
为了更好的理解联邦学习的分类,首先对数据进行定义:
各个企业拥有的数据可以看成是一张表格,表格的每一行是一个带有多个特征(features)以及标签(label)的样本,每一列是一个特征或者标签,例如下图可以是某企业整理的各地房价数据: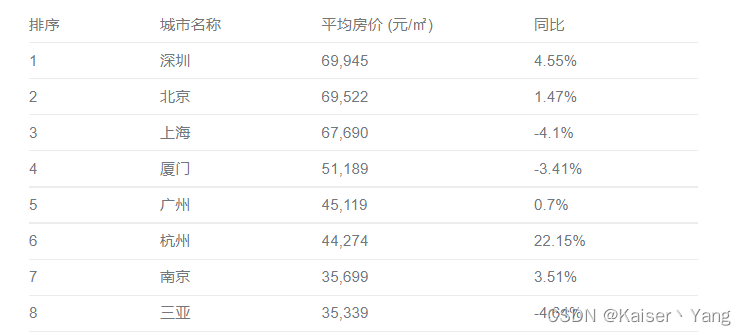
横向联邦学习、纵向联邦学习、联邦迁移学习分类的依据是各个参与方数据相似情况,而联邦强化学习的重点是基于各方环境进行决策(take action)。
3.1 横向联邦学习
横向联邦学习(Horizontal Federated Learning)指的是各方拥有的数据的特征(features)是基本一致的也都拥有各自的标签(label),如果将各方的数据集中成一个中心体,各方拥有的则是中心体的不同样本(横向指的是对中心体进行横向划分)。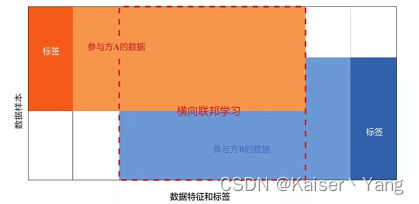
横向联邦学习(带有中心服务器)的过程可以概括为下图: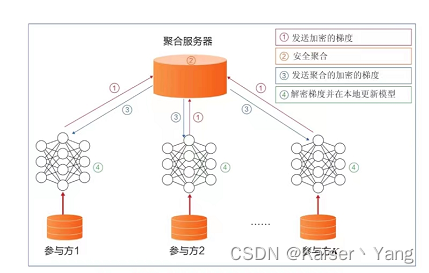
3.2 纵向联邦学习
纵向联邦学习(Vertical Federated Learning)指的是各方拥有的数据有着很多不同的特征,但是可能会有许多相同的样本个体(例如同一个人在银行和保险公司的信息),同样将数据集中成一个中心体的话,各方拥有的是样本的不同属性(纵向指的是对中心体进行纵向划分。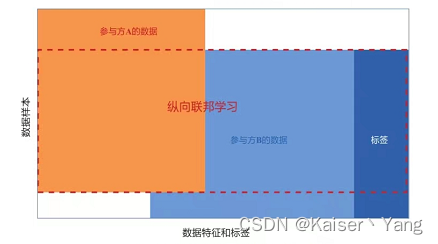
纵向联邦学习实际上只有一方拥有标签,通过纵向联邦学习对相交数据进行训练。
纵向联邦学习的过程要稍微复杂一些,首先需要进行的是数据的对齐,由于不能泄漏数据,是将加密后的数据进行对齐,如下图所示: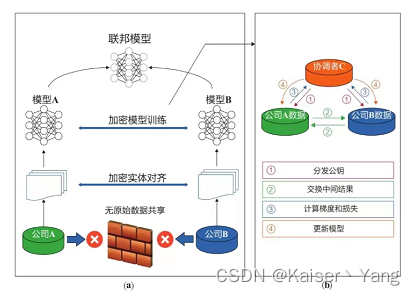
对齐后的数据大致如下(对其操作只会获取两个数据中相交的样本,下图中即U1和U2: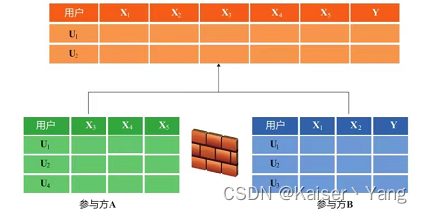
由于只有一方拥有标签,但是双方(以两个参与方为例)进行了预测,这里将损失函数重新定义:
L
=
1
2
∑
(
y
A
(
i
)
+
y
B
(
i
)
−
y
)
2
L=\frac 1 2 \sum(y_A^{(i)}+y_B^{(i)}-y)^2
L=21∑(yA(i)+yB(i)−y)2
而各个模型拥有的参数只有自己涉及特征的参数,以上面的例子为例,也就是:
y
A
(
U
1
)
=
w
3
X
3
+
w
4
X
4
+
w
5
X
5
y
B
(
U
1
)
=
w
1
X
1
+
w
2
X
2
\begin{aligned} &y_A^{(U_1)} = w_3X_3+w_4X_4+w_5X_5\\ &y_B^{(U_1)} = w_1X_1+w_2X_2 \end{aligned}
yA(U1)=w3X3+w4X4+w5X5yB(U1)=w1X1+w2X2
这里只是简单举例,实际上是以矩阵的形式进行,同时会包含多个隐藏层。
这也就表示不管是在训练还是在预测的时候,都需要参与方进行协调,进行数据的交换(参与方需要各自计算自己的预测值与梯度将结果发送给中心服务器进行聚合)。
3.3 联邦迁移学习
联邦迁移学习(Federated Transfer Learning)指的是,参与方数据的重叠很少的情况(产生数据的人不同,数据的特征也大不相同),将数据题整合成中心体的话,会有大量的位置是空白信息,而各个参与方近似拥有的中心体的独立划分。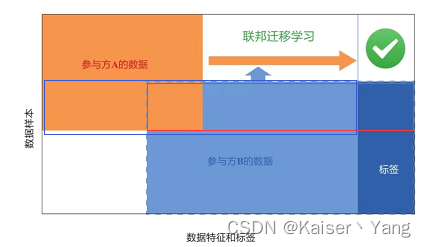
我们定义如下参数:
ϕ \phi ϕ:分类函数,作用于 u i B u_i^B uiB;D c D_c Dc:图中红色方框;D A B D_{AB} DAB:图中蓝色方框。
联邦迁移学习中只有一方拥有标签,通过联邦迁移学习可以利用相交的数据给没有标签的一方数据打上标签。
一个简单的模型如下图所示: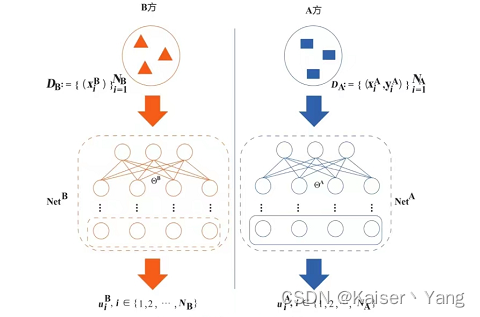
模型的损失函数(不考虑正则):
L
=
L
1
+
γ
L
2
L
1
=
∑
i
N
c
l
o
g
(
1
+
e
−
y
i
ϕ
(
u
i
B
)
)
L
2
=
∑
i
N
A
B
∣
∣
u
i
A
−
u
i
B
∣
∣
F
2
\begin{aligned} &L=L_1+\gamma L_2\\ &L_1=\sum_i^{N_c}log(1+e^{-y_i\phi(u_i^B)})\\ &L_2=\sum_i^{N_{AB}}||u_i^A-u_i^B||^2_F \end{aligned}
L=L1+γL2L1=i∑Nclog(1+e−yiϕ(uiB))L2=i∑NAB∣∣uiA−uiB∣∣F2
上面的公式表表名我们希望最小化两部分(以二分类问题为例标签取值为-1和1):
L 1 L_1 L1:代表与真实标签的接近程度,当 y i = 1 y_i=1 yi=1时要是上式最小 ϕ ( u i B ) \phi(u_i^B) ϕ(uiB)应该尽可能接近 1 1 1,当 y i = − 1 y_i=-1 yi=−1时则应该尽可能接近 − 1 -1 −1;L 2 L_2 L2:代表两个模型representation的相似程度,应为训练两个模型的训练数标签是相同的,所以我们希望两个特征表示(representation)尽可能相似。
3.4 联邦强化学习
联邦强化学习(Federated Reinforcement Learning)指的是将强化学习与联邦学习进行结合,联帮强化学习分为纵向和横向两种,定义与之前类似,横向联邦强化学习(Horizontal Federated Reinforcement Learning)的简单模型如下: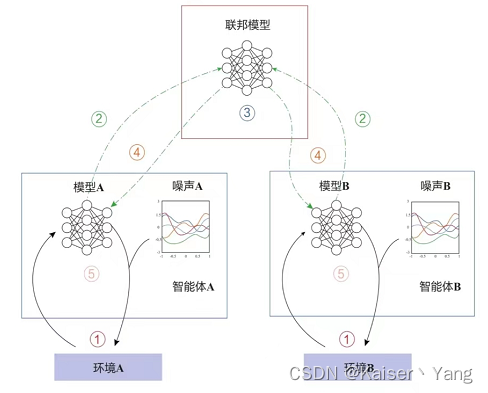
上图中,各自参与方根据自己的环境进行训练,训练出来的模型上传到中央服务器进行聚合后,服务器再下发模型继续进行训练。
纵向联邦强化学习(Vertical Federated Reinforcement Learning)的简单模型如下(图中的虚线表示可以不存在):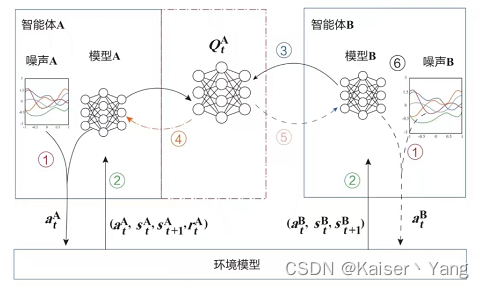
在上图的过程与横向联邦强化学习的过程类似。
4 联邦学习与分布式机器学习

个人认为联邦学习实际上是分布式机器学习的一种变体(variant),传统的分布式机器学习(也叫面向拓展的分布式机器学习)关注的是在硬件资源不够的情况下,如何利用分布式集群对一个庞大的模型进行训练,而联邦学习是,数据本身就在各个节点上,但是由于隐私保护的原因不得不采用类似分布式学习的方法进行学习(这样看来传统的分布式机器学习效果是要好于联邦学习的,因为传统的分布式学习是拥有所有数据的)。而之后提出的面向隐私保护的分布式机器学习,就有点像联邦学习的雏形了。面向隐私保护的分布式机器学习是指参与方拥有相同数据的不同特征,希望在隐私保护的前提下训练出一个模型(可以看到非常想纵向联邦学习)。后面的联邦学习对面向隐私保护的分布式学习进行了拓展。
二者的韦恩图大致如下: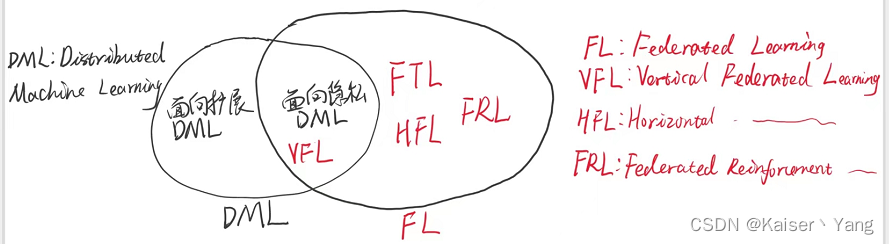
5 REFERENCE
《联邦学习》 杨强等人著
版权归原作者 kaiserqzyue 所有, 如有侵权,请联系我们删除。