LeetCode刷题笔记-数据结构-day15

文章目录

LeetCode刷题笔记-数据结构-day15

108. 将有序数组转换为二叉搜索树

1.题目描述

原题链接：108. 将有序数组转换为二叉搜索树

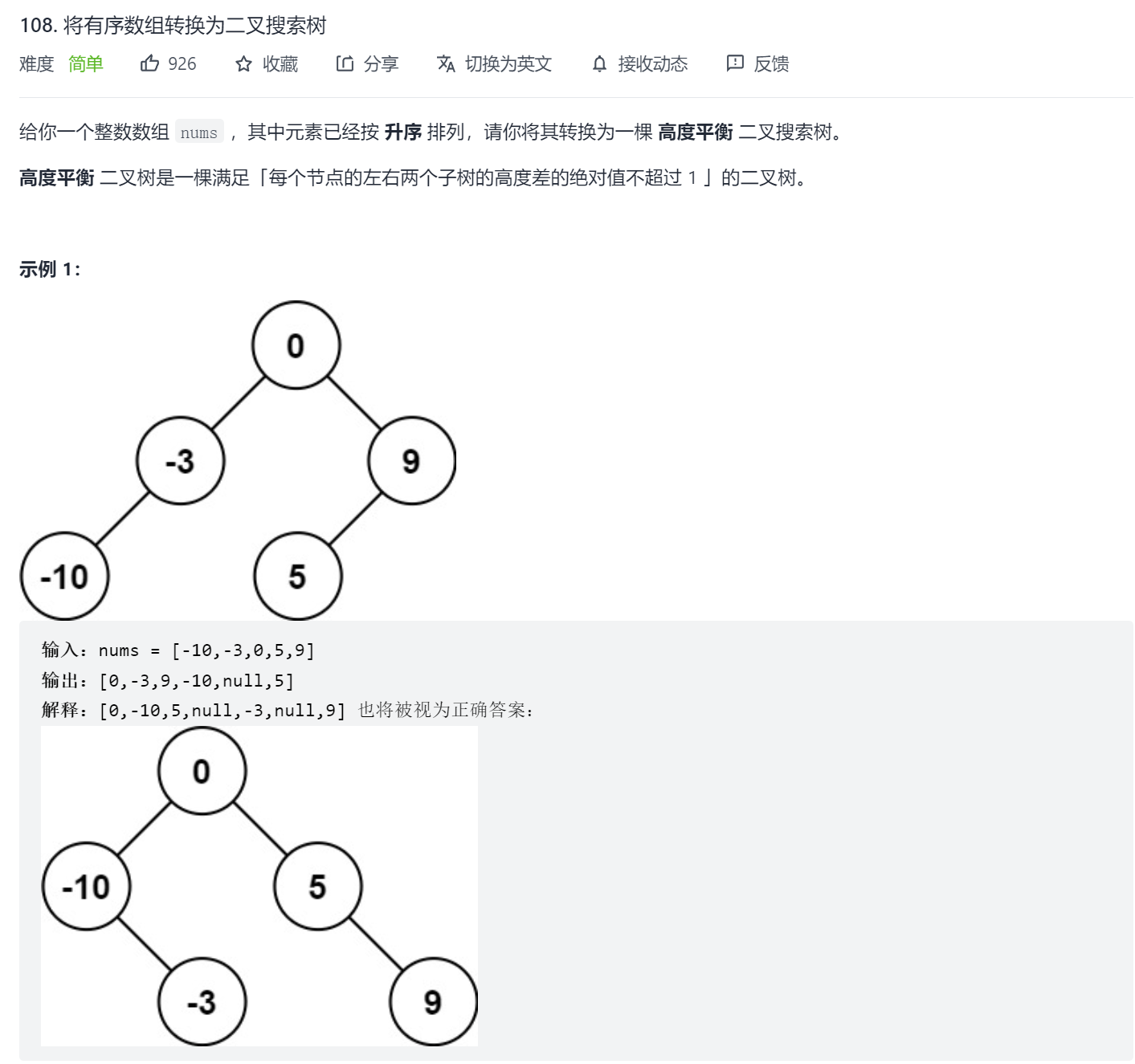
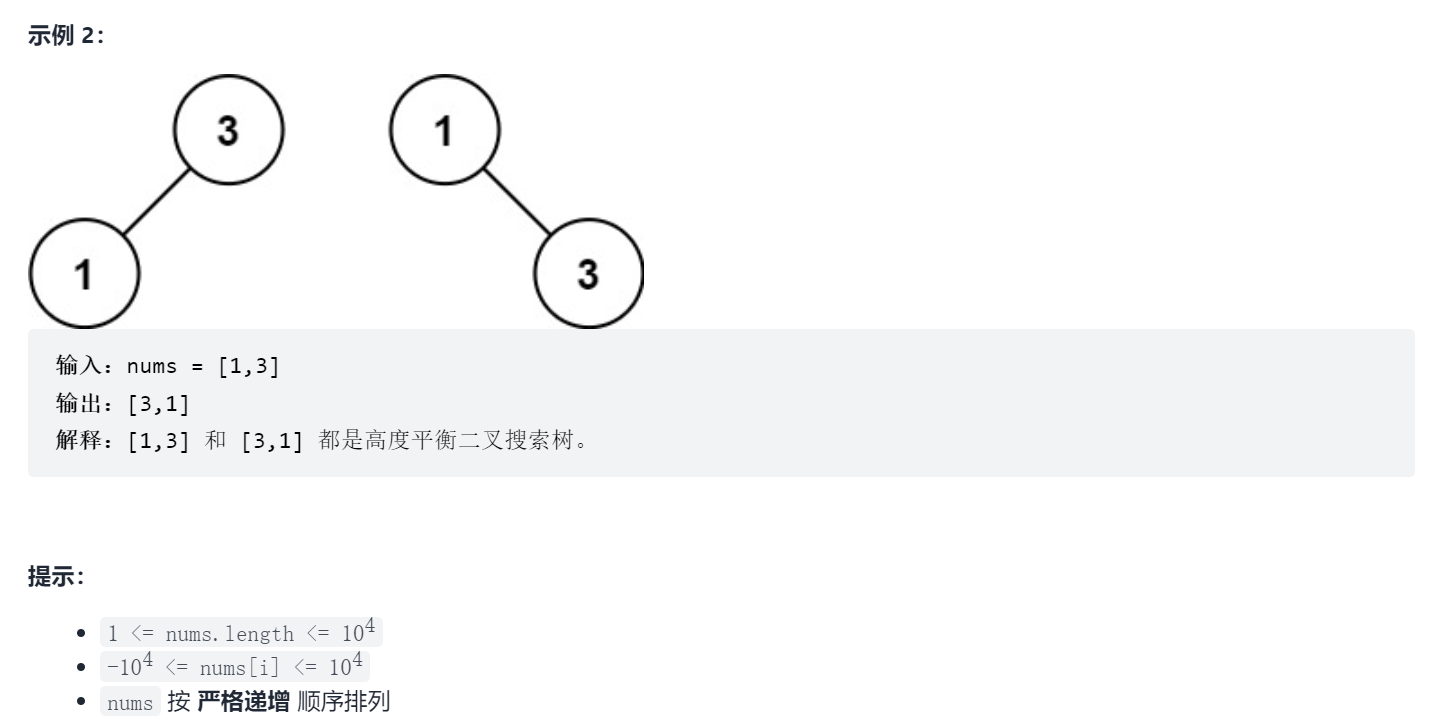
2.解题思路

题目要求：

1. 二叉搜索树：对于所有节点的左子树的值全部小于它，右子树的值全部大于它
2. 每个节点的左右两个子树的高度差的绝对值不超过 1

题目给出了一个升序的数组，我们可以直接从中间的位置

dfs

构建这个二叉树，每次以中点为根，左半部分为左子树，右半部分为右子树。分别递归建立左子树和右子树，根节点的指针指向这两颗子树。

3.代码

classSolution{public:TreeNode*sortedArrayToBST(vector<int>& a){returndfs(a,0,a.size()-1);}TreeNode*dfs(vector<int>& a,int l,int r){if(l>r)return NULL;int t=l+r>>1;TreeNode* root=newTreeNode(a[t]);
        root->left=dfs(a,l,t-1);
        root->right=dfs(a,t+1,r);return root;}};

105. 从前序与中序遍历序列构造二叉树

1.题目描述

原题链接：105. 从前序与中序遍历序列构造二叉树

2.解题思路

算法：递归

具体实现：

1. 使用一个map存储中序遍历的每个值在中序遍历中的位置
2. 利用前序遍历找到根节点的值，也就是前序遍历的第一个数
3. 在中序遍历中根据map找到对应根节点的位置t，则t左边的是左子树的中序遍历，t右边的是右子树的中序遍历
4. 利用中序遍历及t的值可以得到左子树遍历的长度k，则前序遍历根节点后面的k个数为左子树的前序遍历，剩余的为右子树的前序遍历
5. 依照上面的过程递归创建左右子树即可

3.代码

classSolution{public:
    map<int,int> hash;TreeNode*buildTree(vector<int>& pre, vector<int>& ino){int n=ino.size();for(int i=0;i<n;i++) hash[ino[i]]=i;returndfs(pre,ino,0,n-1,0,n-1);}TreeNode*dfs(vector<int>& pre,vector<int>& ino,int pl,int pr,int il,int ir){if(il>ir)return NULL;TreeNode* root=newTreeNode(pre[pl]);int t=hash[pre[pl]];int k=t-il;
        root->left=dfs(pre,ino,pl+1,pl+k,il,il+k-1);
        root->right=dfs(pre,ino,pl+k+1,pr,il+k+1,ir);return root;}};

103. 二叉树的锯齿形层序遍历

1.题目描述

原题链接：103. 二叉树的锯齿形层序遍历

2.解题思路

算法：队列+bfs

1. 初始化一个队列存储每一层的节点，先加入根节点root
2. 遍历队列，取出该层节点，并将其加入队列v，表示这层的答案
3. 取出节点时，需要从左到右将子节点入队
4. 最后加入v到最终答案res时，需要保证锯齿形层序遍历
5. 我们这里用一个bool变量f表示，初始值为true，每遍历一层f=!f
6. 如果为f为false则将v翻转在加入

3.代码

classSolution{public:
    vector<vector<int>>zigzagLevelOrder(TreeNode* root){
        vector<vector<int>> res;if(!root)return res;
        queue<TreeNode*> q;
        q.push(root);
        bool f=true;while(q.size()){int k=q.size();
            vector<int> v;while(k--){
                auto t=q.front();
                q.pop();
                v.push_back(t->val);if(t->left) q.push(t->left);if(t->right) q.push(t->right);}if(!f)reverse(v.begin(),v.end());
            res.push_back(v);
            f=!f;}return res;}};