一、模糊关系的定义
- 集合的直积
设有两个集合X,Y,X和Y的直积X×Y(笛卡尔积)定义为:
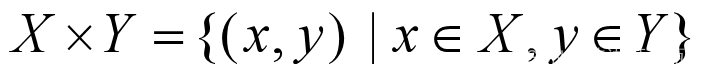
它是由序偶(x,y)的全体所构成的二维论域上的集合。一般来说X×Y≠Y×X。
- 模糊关系及模糊矩阵
设X、Y是两个非空集合,以直积X×Y为论域定义的模糊集合R称为X和Y的模糊关系,记为Rx×y。
(1)模糊关系Rx×y由其隶属函数μR(x,y)完全刻画,μR(x,y)表示了X中的元素x和Y中的元素y具有关系Rx×y的程度。
(2)当X和Y为有限离散集合时,设X={x1,x2,…,xn},Y={y1,y2,…,ym},则X和Y的模糊关系Rx×y可用n×m阶矩阵(模糊矩阵)表示,即
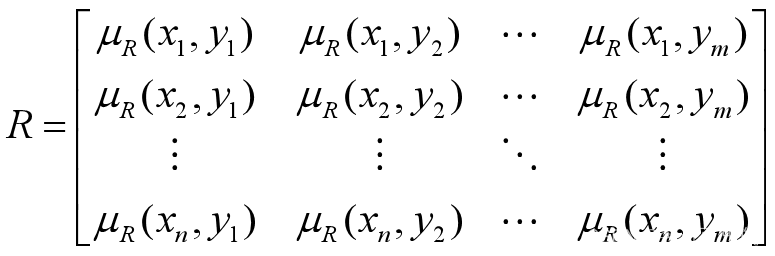
模糊矩阵是论域为直积X×Y的模糊集。
模糊关系和模糊矩阵举例如下
例:X={10,20,40,80},Y={10,20,30,40},“x远大于y”这一模糊关系的模糊关系矩阵为

结论:当x=40,y=20时,“x远大于y”的程度是0.8。
- 模糊集合的直积
若有两个模糊集A和B,其论域分别X和Y,定义在积空间X×Y上的模糊集合A×B称为模糊集合A和B的直积,其隶属函数为:
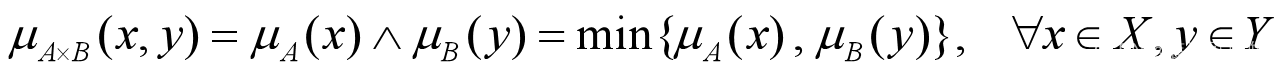
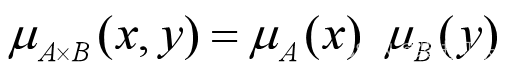
模糊集合A和B的直积是积空间X×Y上的一个模糊关系。
二、模糊关系和模糊矩阵的合成运算
由于模糊关系和模糊矩阵是定义在直积空间的模糊集合,因此它遵从一般模糊集合(并、交、补等)的运算规则。(详见一)
1.模糊矩阵的合成运算
例子引入:已知模糊关系矩阵






总结来说,就是R1的行与R2的列放在一起比较,先求出最小的(从第二行等号到第三行等号),再求出最小之中最大的那个数字,作为最终结果(从第三行到第四行)。
- 合成运算和直积运算的关系
设A为论域X上的模糊集合,B为论域Y上的模糊集合。根据上述模糊集合的直积和模糊矩阵的合成的定义,当X和Y为离散论域时,A与B的直积(取小运算)为:
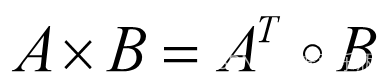
3.模糊关系的合成运算
设R1是X和Y的模糊关系,R2是Y和Z的模糊关系,R1和R2的合成R1○R2指的是X×Z上的一个模糊关系,其隶属函数为:
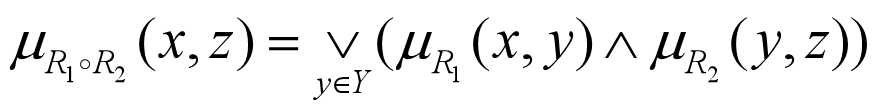
在上式中,“∨”表示取大运算,“∧”表示取小运算,因此称为取大-取小合成(max-min composition)。
PS:一个小形象的比喻,对于一个模糊关系,其对应的隶属度函数就相当于它的身份证。
当论域X、Y、Z为有限集时,可用模糊矩阵的合成来表示模糊关系的合成。
三、模糊逻辑与模糊推理
- 模糊语言变量
模糊语言变量(linguistic variables)是自然语言中的词或句,如气温、误差等,它的取值不是通常的常数,而是用模糊语言表示的模糊集。以下将模糊语言变量简称语言变量。
一个语言变量可由以下的五元体来表征:
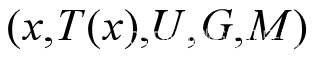
x为语言变量的名称;T(x)语言变量值的集合;U为x的论域;G为语法规则(用于产生各语言变量值x的名称);M为语义规则(用于产生模糊集合的隶属函数)。
- 模糊命题
(1)模糊命题(proposition):含有模糊概念的陈述句。模糊命题可以用英文字母表示,如P:误差较大。
(2)模糊命题的真值:模糊命题的真假程度,它是[0,1]区间上的一个实数。
(3)单模糊命题:简单的模糊陈述句,其一般形式为 P:x 为 A x为模糊变量,A为某一模糊概念对应的模糊集合。
(4)单模糊命题P的真值V(P),就由该变量对模糊集的隶属度来表示,即
V(P)=μA(x)
当μA(x)=0,表示命题P完全假;μA(x)=1,表示命题P完全真;μA(x)越接近0,命题P假的程度越大,真的程度越小;μA(x)越接近1,命题P假的程度越小,真的程度越大。
例:讨论模糊命题Q:天气热。语言变量是气温t,t属于[-40ºC,50ºC],定义“热”的模糊集合为H,其隶属函数为μH(t)。若今日气温为t=20 ºC,μH(20)=0.4,那么该命题的真值为0.4。也就是说,“天气热”这个命题的真实程度是0.4。
(5)复合模糊命题:把简单模糊命题通过联结词联合起来,就构成了复合模糊命题。联结词可以是“与”、“或”、“非”、“若……则……”等。
(6) 条件模糊命题: “IF … THEN …”形式的条件语句,表达两个普通命题之间的因果关系,称为条件模糊命题。
- 模糊推理
模糊推理(Fuzzy Inference)是不确定性推理方法的一种,它是运用模糊语言,对模糊命题进行模糊判断,推出一个近似的模糊结论的方法。
(1)模糊推理的基本形式:三段论

(2)模糊推理的合成规则
1975年Zadeh提出了模糊逻辑推理的合成规则。

即结论B′是模糊集合A′和模糊蕴含关系A→B的合成。
合成推理规则举例
若人工调节炉温,有如下的经验规则:“如果炉温低,则应施加高电压”。试问当炉温为“非常低”时,应施加怎样的电压。已知:x和y分别表示模糊语言变量“炉温”和“电压”,x和y的论域为:

(3)多重模糊条件语句
1)使用“and”连接的模糊条件语句
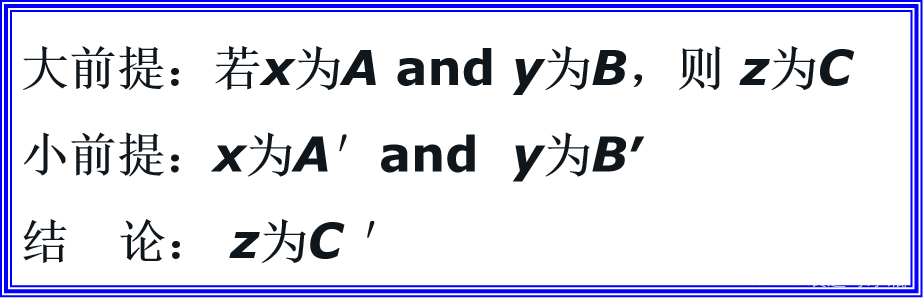
模糊蕴含关系:

推理结果/运算方式:
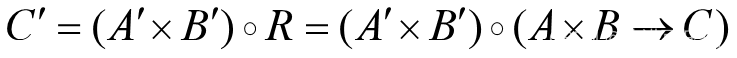
步骤如下:求规则的模糊蕴含关系,求AXB;进而求R;
计算输入量的模糊集合,求A'、B';
计算输出量的模糊集合,求C'。
2)使用“also”连接的模糊条件语句

推理结果/运算方式:
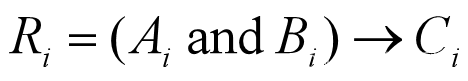
步骤如下:求每条规则的模糊蕴含关系,求R1、R2;
求总模糊蕴含关系,求R;
计算输入量的模糊集合,求A'XB';
计算输出量的模糊集合,求C‘。
本人自用学习笔记,如有问题请与我联系 。
版权归原作者 装进可乐瓶 所有, 如有侵权,请联系我们删除。