这个实验的要求写的还是挺清楚的(与上学期相比),本博客采用python实现,科学计算库采用
numpy
,作图采用
matplotlib.pyplot
,为了简便在文件开头import如下:
import numpy as np
import matplotlib.pyplot as plt
本实验用到的numpy函数
一般把
numpy
简写为
np
(import numpy as np)。下面简单介绍一下实验中用到的numpy函数。下面的代码均需要在最前面加上
import numpy as np
。
np.array
该函数返回一个
numpy.ndarray
对象,可以理解为一个多维数组(本实验中仅会用到一维(可以当作列向量)和二维(矩阵))。下面用小写的
x
\pmb x
xx表示列向量,大写的
A
A
A表示矩阵。
A.T
表示
A
A
A的转置。对
ndarray
的运算一般都是逐元素的。
>>> x = np.array([1,2,3])>>> x
array([1,2,3])>>> A = np.array([[2,3,4],[5,6,7]])>>> A
array([[2,3,4],[5,6,7]])>>> A.T # 转置
array([[2,5],[3,6],[4,7]])>>> A +1
array([[3,4,5],[6,7,8]])>>> A *2
array([[4,6,8],[10,12,14]])
np.random
np.random
模块中包含几个生成随机数的函数。在本实验中用随机初始化参数(梯度下降法),给数据添加噪声。
>>> np.random.rand(3,3)# 生成3 * 3 随机矩阵,每个元素服从[0,1)均匀分布
array([[8.18713933e-01,5.46592778e-01,1.36380542e-01],[9.85514865e-01,7.07323389e-01,2.51858374e-04],[3.14683662e-01,4.74980699e-02,4.39658301e-01]])>>> np.random.rand(1)# 生成单个随机数
array([0.70944563])>>> np.random.rand(5)# 长为5的一维随机数组
array([0.03911319,0.67572368,0.98884287,0.12501456,0.39870096])>>> np.random.randn(3,3)# 同上,但每个元素服从N(0, 1)(标准正态)
数学函数
本实验中只用到了
np.sin
。这些数学函数是对
np.ndarray
逐元素操作的:
>>> x = np.array([0,3.1415,3.1415/2])# 0, pi, pi / 2>>> np.round(np.sin(x))# 先求sin再四舍五入: 0, 0, 1
array([0.,0.,1.])
此外,还有
np.log
、
np.exp
等与python的
math
库相似的函数(只不过是对多维数组进行逐元素运算)。
np.dot
返回两个矩阵的乘积。与线性代数中的矩阵乘法一致。要求第一个矩阵的列等于第二个矩阵的行数。特殊地,当其中一个为一维数组时,形状会自动适配为
n
×
1
n\times1
n×1或
1
×
n
.
1\times n.
1×n.
>>> x = np.array([1,2,3])# 一维数组>>> A = np.array([[1,1,1],[2,2,2],[3,3,3]])# 3 * 3矩阵>>> np.dot(x,A)
array([14,14,14])>>> np.dot(A,x)
array([6,12,18])>>> x_2D = np.array([[1,2,3]])# 这是一个二维数组(1 * 3矩阵)>>> np.dot(x_2D, A)# 可以运算
array([[14,14,14]])>>> np.dot(A, x_2D)# 行列不匹配
Traceback (most recent call last):
File "<stdin>", line 1,in<module>
File "<__array_function__ internals>", line 5,in dot
ValueError: shapes (3,3)and(1,3)not aligned:3(dim 1)!=1(dim 0)
np.eye
np.eye(n)
返回一个n阶单位阵。
>>> A = np.eye(3)>>> A
array([[1.,0.,0.],[0.,1.,0.],[0.,0.,1.]])
线性代数相关
np.linalg
是与线性代数有关的库。
>>> A
array([[1,0,0],[0,2,0],[0,0,3]])>>> np.linalg.inv(A)# 求逆(本实验不考虑逆不存在)
array([[1.,0.,0.],[0.,0.5,0.],[0.,0.,0.33333333]])>>> x = np.array([1,2,3])>>> np.linalg.norm(x)# 返回向量x的模长(平方求和开根号)3.7416573867739413>>> np.linalg.eigvals(A)# A的特征值
array([1.,2.,3.])
生成数据
生成数据要求加入噪声(误差)。上课讲的时候举的例子就是正弦函数,我们这里也采用标准的正弦函数
y
=
sin
x
.
y=\sin x.
y=sinx.(加入噪声后即为
y
=
sin
x
+
ϵ
,
y=\sin x+\epsilon,
y=sinx+ϵ,其中
ϵ
∼
N
(
0
,
σ
2
)
\epsilon\sim N(0, \sigma^2)
ϵ∼N(0,σ2),由于
sin
x
\sin x
sinx的最大值为
1
1
1,我们把误差的方差设小一点,这里设成
1
25
\frac{1}{25}
251)。
'''
返回数据集,形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1], 默认为(0, 10)
'''defget_dataset(N =100, bound =(0,10)):
l, r = bound
# np.random.rand 产生[0, 1)的均匀分布,再根据l, r缩放平移# 这里sort是为了画图时不会乱,可以去掉sorted试一试
x =sorted(np.random.rand(N)*(r - l)+ l)# np.random.randn 产生N(0,1),除以5会变为N(0, 1 / 25)
y = np.sin(x)+ np.random.randn(N)/5return np.array([x,y]).T
产生的数据集每行为一个平面上的点。产生的数据看起来像这样: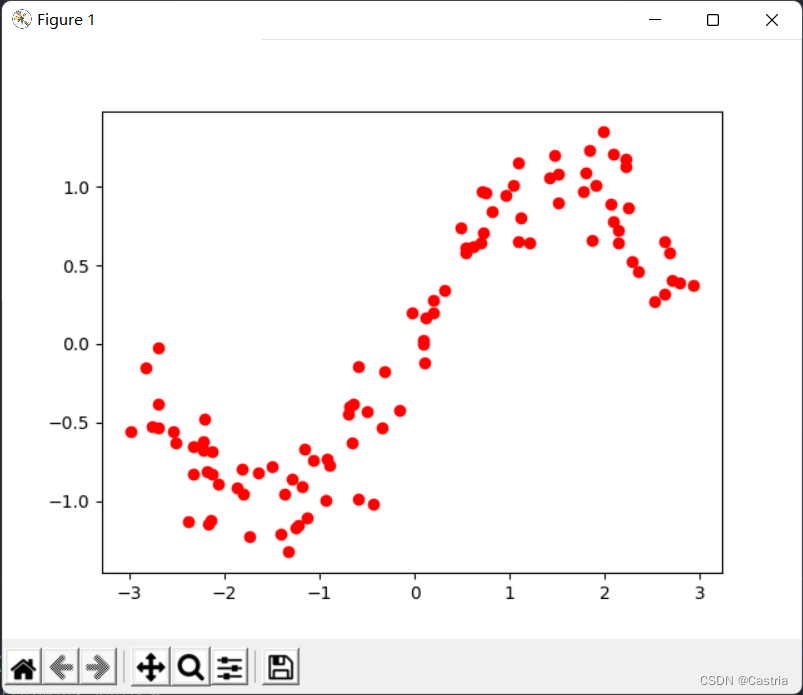
隐隐约约能看出来是个正弦函数的形状。产生上面图像的代码如下:
dataset = get_dataset(bound =(-3,3))# 绘制数据集散点图for[x, y]in dataset:
plt.scatter(x, y, color ='red')
plt.show()
最小二乘法拟合
下面我们分别用四种方法(最小二乘,正则项/岭回归,梯度下降法,共轭梯度法)以用多项式拟合上述干扰过的正弦曲线。
解析解推导
简单回忆一下最小二乘法的原理:现在我们想用一个
m
m
m次多项式
f
(
x
)
=
w
0
+
w
1
x
+
w
2
x
2
+
.
.
.
+
w
m
x
m
f(x)=w_0+w_1x+w_2x^2+...+w_mx^m
f(x)=w0+w1x+w2x2+...+wmxm
来近似真实函数
y
=
sin
x
.
y=\sin x.
y=sinx.我们的目标是最小化数据集
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
N
,
y
N
)
(x_1,y_1),(x_2,y_2),...,(x_N,y_N)
(x1,y1),(x2,y2),...,(xN,yN)上的损失
L
L
L(loss),这里损失函数采用平方误差:
L
=
∑
i
=
1
N
[
y
i
−
f
(
x
i
)
]
2
L=\sum\limits_{i=1}^N[y_i-f(x_i)]^2
L=i=1∑N[yi−f(xi)]2
为了求得使均方误差最小(因此最贴合目标曲线)的参数
w
0
,
w
1
,
.
.
.
,
w
m
,
w_0,w_1,...,w_m,
w0,w1,...,wm,我们需要分别求损失
L
L
L关于
w
0
,
w
1
,
.
.
.
,
w
m
w_0,w_1,...,w_m
w0,w1,...,wm的导数。为了方便,我们采用线性代数的记法:
X
=
(
1
x
1
x
1
2
⋯
x
1
m
1
x
2
x
2
2
⋯
x
2
m
⋮
⋮
1
x
N
x
N
2
⋯
x
N
m
)
N
×
(
m
+
1
)
,
Y
=
(
y
1
y
2
⋮
y
N
)
N
×
1
,
W
=
(
w
0
w
1
⋮
w
m
)
(
m
+
1
)
×
1
.
X=\begin{pmatrix}1 & x_1 & x_1^2 & \cdots & x_1^m\\ 1 & x_2 & x_2^2 & \cdots & x_2^m\\ \vdots & & & &\vdots\\ 1 & x_N & x_N^2 & \cdots & x_N^m\\\end{pmatrix}_{N\times(m+1)},Y=\begin{pmatrix}y_1 \\ y_2 \\ \vdots \\y_N\end{pmatrix}_{N\times1},W=\begin{pmatrix}w_0 \\ w_1 \\ \vdots \\w_m\end{pmatrix}_{(m+1)\times1}.
X=⎝⎛11⋮1x1x2xNx12x22xN2⋯⋯⋯x1mx2m⋮xNm⎠⎞N×(m+1),Y=⎝⎛y1y2⋮yN⎠⎞N×1,W=⎝⎛w0w1⋮wm⎠⎞(m+1)×1.
在这种表示方法下,有
(
f
(
x
1
)
f
(
x
2
)
⋮
f
(
x
N
)
)
=
X
W
.
\begin{pmatrix}f(x_1)\\ f(x_2) \\ \vdots \\ f(x_N)\end{pmatrix}= XW.
⎝⎛f(x1)f(x2)⋮f(xN)⎠⎞=XW.
如果有疑问可以自己拿矩阵乘法验证一下。继续,误差项之和可以表示为
(
f
(
x
1
)
−
y
1
f
(
x
2
)
−
y
2
⋮
f
(
x
N
)
−
y
N
)
=
X
W
−
Y
.
\begin{pmatrix}f(x_1)-y_1 \\ f(x_2)-y_2 \\ \vdots \\ f(x_N)-y_N\end{pmatrix}=XW-Y.
⎝⎛f(x1)−y1f(x2)−y2⋮f(xN)−yN⎠⎞=XW−Y.
因此,损失函数
L
=
(
X
W
−
Y
)
T
(
X
W
−
Y
)
.
L=(XW-Y)^T(XW-Y).
L=(XW−Y)T(XW−Y).
(为了求得向量
x
=
(
x
1
,
x
2
,
.
.
.
,
x
N
)
T
\pmb x=(x_1,x_2,...,x_N)^T
xx=(x1,x2,...,xN)T各分量的平方和,可以对
x
\pmb x
xx作内积,即
x
T
x
.
\pmb x^T \pmb x.
xxTxx.)
为了求得使
L
L
L最小的
W
W
W(这个
W
W
W是一个列向量),我们需要对
L
L
L求偏导数,并令其为
0
:
0:
0:
∂
L
∂
W
=
∂
∂
W
[
(
X
W
−
Y
)
T
(
X
W
−
Y
)
]
=
∂
∂
W
[
(
W
T
X
T
−
Y
T
)
(
X
W
−
Y
)
]
=
∂
∂
W
(
W
T
X
T
X
W
−
W
T
X
T
Y
−
Y
T
X
W
+
Y
T
Y
)
=
∂
∂
W
(
W
T
X
T
X
W
−
2
Y
T
X
W
+
Y
T
Y
)
(
容易验证
,
W
T
X
T
Y
=
Y
T
X
W
,
因而可以将其合并
)
=
2
X
T
X
W
−
2
X
T
Y
\begin{aligned}\frac{\partial L}{\partial W}&=\frac{\partial}{\partial W}[(XW-Y)^T(XW-Y)]\\ &=\frac{\partial}{\partial W}[(W^TX^T-Y^T)(XW-Y)] \\ &=\frac{\partial}{\partial W}(W^TX^TXW-W^TX^TY-Y^TXW+Y^TY)\\ &=\frac{\partial}{\partial W}(W^TX^TXW-2Y^TXW+Y^TY)(容易验证,W^TX^TY=Y^TXW,因而可以将其合并)\\ &=2X^TXW-2X^TY\end{aligned}
∂W∂L=∂W∂[(XW−Y)T(XW−Y)]=∂W∂[(WTXT−YT)(XW−Y)]=∂W∂(WTXTXW−WTXTY−YTXW+YTY)=∂W∂(WTXTXW−2YTXW+YTY)(容易验证,WTXTY=YTXW,因而可以将其合并)=2XTXW−2XTY
说明:
(1)从第3行到第4行,由于
W
T
X
T
Y
W^TX^TY
WTXTY和
Y
T
X
W
Y^TXW
YTXW都是数(或者说
1
×
1
1\times1
1×1矩阵),二者互为转置,因此值相同,可以合并成一项。
(2)从第4行到第5行的矩阵求导,第一项
∂
∂
W
(
W
T
(
X
T
X
)
W
)
\frac{\partial}{\partial W}(W^T(X^TX)W)
∂W∂(WT(XTX)W)是一个关于
W
W
W的二次型,其导数就是
2
X
T
X
W
.
2X^TXW.
2XTXW.
(3)对于一次项
−
2
Y
T
X
W
-2Y^TXW
−2YTXW的求导,如果按照实数域的求导应该得到
−
2
Y
T
X
.
-2Y^TX.
−2YTX.但检查一下发现矩阵的型对不上,需要做一下转置,变为
−
2
X
T
Y
.
-2X^TY.
−2XTY.
矩阵求导线性代数课上也没有系统教过,只对这里出现的做一下说明。(多了我也不会 )
令偏导数为0,得到
X
T
X
W
=
Y
T
X
,
X^TXW=Y^TX,
XTXW=YTX,
左乘
(
X
T
X
)
−
1
(X^TX)^{-1}
(XTX)−1(
X
T
X
X^TX
XTX的可逆性见下方的补充说明),得到
W
=
(
X
T
X
)
−
1
X
T
Y
.
W=(X^TX)^{-1}X^TY.
W=(XTX)−1XTY.
这就是我们想求的
W
W
W的解析解,我们只需要调用函数算出这个值即可。
'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''deffit(dataset, m =5):
X = np.array([dataset[:,0]** i for i inrange(m +1)]).T
Y = dataset[:,1]return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)
稍微解释一下代码:第一行即生成上面约定的
X
X
X矩阵,
dataset[:,0]
即数据集第0列
(
x
1
,
x
2
,
.
.
.
,
x
N
)
T
(x_1,x_2,...,x_N)^T
(x1,x2,...,xN)T;第二行即
Y
Y
Y矩阵;第三行返回上面的解析解。(如果不熟悉python语法或者
numpy
库还是挺不友好的)
简单地验证一下我们已经完成的函数的结果:为此,我们先写一个
draw
函数,用于把求得的
W
W
W对应的多项式
f
(
x
)
f(x)
f(x)画到
pyplot
库的图像上去:
'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''defdraw(dataset, w, color ='red', label =''):
X = np.array([dataset[:,0]** i for i inrange(len(w))]).T
Y = np.dot(X, w)
plt.plot(dataset[:,0], Y, c = color, label = label)
然后是主函数:
if __name__ =='__main__':
dataset = get_dataset(bound =(-3,3))# 绘制数据集散点图for[x, y]in dataset:
plt.scatter(x, y, color ='red')# 最小二乘
coef1 = fit(dataset)
draw(dataset, coef1, color ='black', label ='OLS')# 绘制图像
plt.legend()
plt.show()
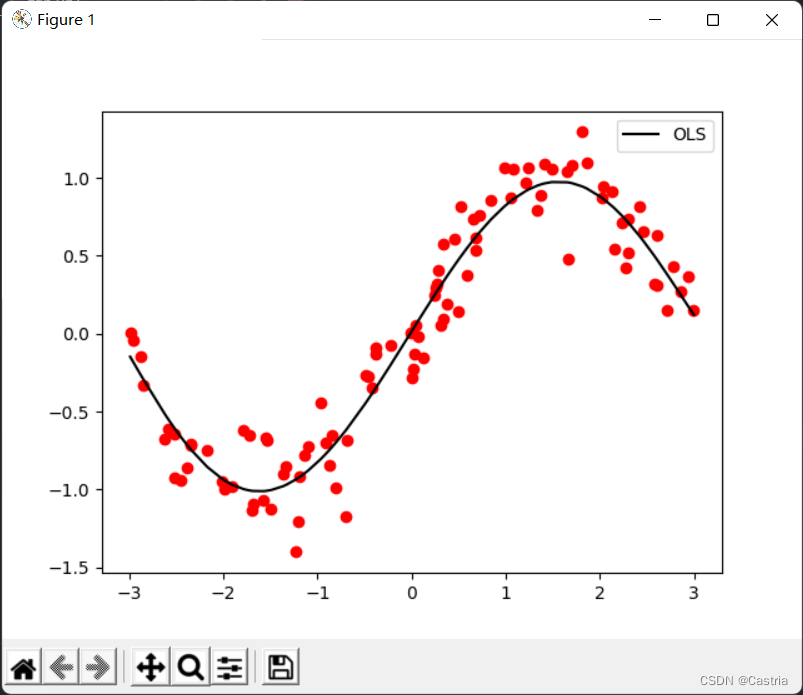
可以看到5次多项式拟合的效果还是比较不错的(数据集每次随机生成,所以跟第一幅图不一样)。
截至这部分全部的代码,后面同名函数不再给出说明:
import numpy as np
import matplotlib.pyplot as plt
'''
返回数据集,形如[[x_1, y_1], [x_2, y_2], ..., [x_N, y_N]]
保证 bound[0] <= x_i < bound[1].
- N 数据集大小, 默认为 100
- bound 产生数据横坐标的上下界, 应满足 bound[0] < bound[1]
'''defget_dataset(N =100, bound =(0,10)):
l, r = bound
x =sorted(np.random.rand(N)*(r - l)+ l)
y = np.sin(x)+ np.random.randn(N)/5return np.array([x,y]).T
'''
最小二乘求出解析解, m 为多项式次数
最小二乘误差为 (XW - Y)^T*(XW - Y)
- dataset 数据集
- m 多项式次数, 默认为 5
'''deffit(dataset, m =5):
X = np.array([dataset[:,0]** i for i inrange(m +1)]).T
Y = dataset[:,1]return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), Y)'''
绘制给定系数W的, 在数据集上的多项式函数图像
- dataset 数据集
- w 通过上面四种方法求得的系数
- color 绘制颜色, 默认为 red
- label 图像的标签
'''defdraw(dataset, w, color ='red', label =''):
X = np.array([dataset[:,0]** i for i inrange(len(w))]).T
Y = np.dot(X, w)
plt.plot(dataset[:,0], Y, c = color, label = label)if __name__ =='__main__':
dataset = get_dataset(bound =(-3,3))# 绘制数据集散点图for[x, y]in dataset:
plt.scatter(x, y, color ='red')
coef1 = fit(dataset)
draw(dataset, coef1, color ='black', label ='OLS')
plt.legend()
plt.show()
补充说明
上面有一块不太严谨:对于一个矩阵
X
X
X而言,
X
T
X
X^TX
XTX不一定可逆。然而在本实验中,可以证明其为可逆矩阵。由于这门课不是线性代数课,我们就不费太多篇幅介绍这个了,仅作简单提示:
(1)
X
X
X是一个
N
×
(
m
+
1
)
N\times(m+1)
N×(m+1)的矩阵。其中数据数
N
N
N远大于多项式次数
m
m
m,有
N
>
m
+
1
;
N>m+1;
N>m+1;
(2)为了说明
X
T
X
X^TX
XTX可逆,需要说明
(
X
T
X
)
(
m
+
1
)
×
(
m
+
1
)
(X^TX)_{(m+1)\times(m+1)}
(XTX)(m+1)×(m+1)满秩,即
R
(
X
T
X
)
=
m
+
1
;
R(X^TX)=m+1;
R(XTX)=m+1;
(3)在线性代数中,我们证明过
R
(
X
)
=
R
(
X
T
)
=
R
(
X
T
X
)
=
R
(
X
X
T
)
;
R(X)=R(X^T)=R(X^TX)=R(XX^T);
R(X)=R(XT)=R(XTX)=R(XXT);
(4)
X
X
X是一个范德蒙矩阵,由其性质可知其秩等于
m
i
n
{
N
,
m
+
1
}
=
m
+
1.
min\{N,m+1\}=m+1.
min{N,m+1}=m+1.
添加正则项(岭回归)
最小二乘法容易造成过拟合。为了说明这种缺陷,我们用所生成数据集的前50个点进行训练(这样抽样不够均匀,这里只是为了说明过拟合),得出参数,再画出整个函数图像,查看拟合效果:
if __name__ =='__main__':
dataset = get_dataset(bound =(-3,3))# 绘制数据集散点图for[x, y]in dataset:
plt.scatter(x, y, color ='red')# 取前50个点进行训练
coef1 = fit(dataset[:50], m =3)# 再画出整个数据集上的图像
draw(dataset, coef1, color ='black', label ='OLS')
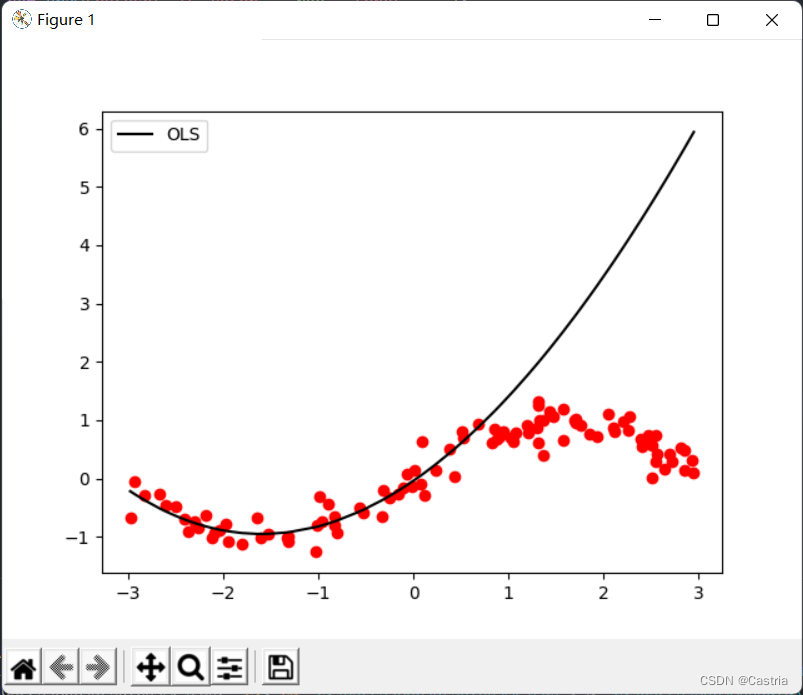
过拟合在
m
m
m较大时尤为严重(上面图像为
m
=
3
m=3
m=3时)。当多项式次数升高时,为了尽可能贴近所给数据集,计算出来的系数的数量级将会越来越大,在未见样本上的表现也就越差。如上图,可以看到拟合在前50个点(大约在横坐标
[
−
3
,
0
]
[-3,0]
[−3,0]处)表现很好;而在测试集上表现就很差(
[
0
,
3
]
[0,3]
[0,3]处)。为了防止过拟合,可以引入正则化项。此时损失函数
L
L
L变为
L
=
(
X
W
−
Y
)
T
(
X
W
−
Y
)
+
λ
∣
∣
W
∣
∣
2
2
L=(XW-Y)^T(XW-Y)+\lambda||W||_2^2
L=(XW−Y)T(XW−Y)+λ∣∣W∣∣22
其中
∣
∣
⋅
∣
∣
2
2
||\cdot||_2^2
∣∣⋅∣∣22表示
L
2
L_2
L2范数的平方,在这里即
W
T
W
;
λ
W^TW;\lambda
WTW;λ为正则化系数。该式子也称岭回归(Ridge Regression)。它的思想是兼顾损失函数与所得参数
W
W
W的模长(在
L
2
L_2
L2范数时),防止
W
W
W内的参数过大。
举个例子(数是随便编的):当正则化系数为
1
1
1,若方案1在数据集上的平方误差为
0.5
,
0.5,
0.5,此时
W
=
(
100
,
−
200
,
300
,
150
)
T
W=(100,-200,300,150)^T
W=(100,−200,300,150)T;方案2在数据集上的平方误差为
10
,
10,
10,此时
W
=
(
1
,
−
3
,
2
,
1
)
W=(1,-3,2,1)
W=(1,−3,2,1),那我们选择方案2的
W
.
W.
W.正则化系数
λ
\lambda
λ刻画了这种对于
W
W
W模长的重视程度:
λ
\lambda
λ越大,说明
W
W
W的模长升高带来的惩罚也就越大。当
λ
=
0
,
\lambda=0,
λ=0,岭回归即变为普通的最小二乘法。与岭回归相似的还有LASSO,就是将正则化项换为
L
1
L_1
L1范数。
重复上面的推导,我们可以得出解析解为
W
=
(
X
T
X
+
λ
E
m
+
1
)
−
1
X
T
Y
.
W=(X^TX+\lambda E_{m+1})^{-1}X^TY.
W=(XTX+λEm+1)−1XTY.
其中
E
m
+
1
E_{m+1}
Em+1为
m
+
1
m+1
m+1阶单位阵。容易得到
(
X
T
X
+
λ
E
m
+
1
)
(X^TX+\lambda E_{m+1})
(XTX+λEm+1)也是可逆的。
该部分代码如下。
'''
岭回归求解析解, m 为多项式次数, l 为 lambda 即正则项系数
岭回归误差为 (XW - Y)^T*(XW - Y) + λ(W^T)*W
- dataset 数据集
- m 多项式次数, 默认为 5
- l 正则化参数 lambda, 默认为 0.5
'''defridge_regression(dataset, m =5, l =0.5):
X = np.array([dataset[:,0]** i for i inrange(m +1)]).T
Y = dataset[:,1]return np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)+ l * np.eye(m +1)), X.T), Y)
两种方法的对比如下: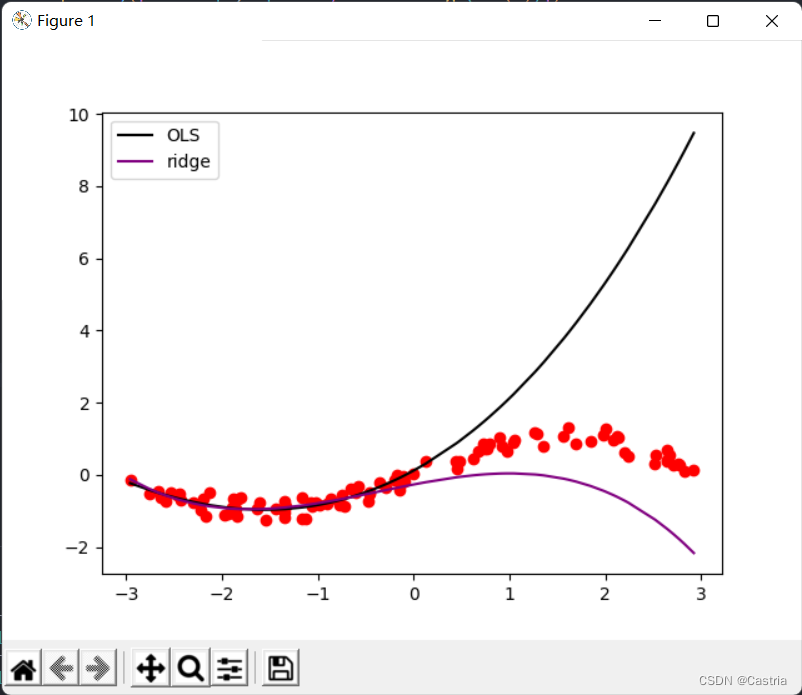
对比可以看出,岭回归显著减轻了过拟合(此时为
m
=
3
,
λ
=
0.3
m=3,\lambda=0.3
m=3,λ=0.3)。
梯度下降法
梯度下降法并不是求解该问题的最好方法,很容易就无法收敛。先简单介绍梯度下降法的基本思想:若我们想求取复杂函数
f
(
x
)
f(x)
f(x)的最小值(最值点)(这个
x
x
x可能是向量等),即
x
m
i
n
=
arg min
x
f
(
x
)
x_{min}=\argmin_{x}f(x)
xmin=xargminf(x)
梯度下降法重复如下操作:
(0)(随机)初始化
x
0
(
t
=
0
)
x_0(t=0)
x0(t=0);
(1)设
f
(
x
)
f(x)
f(x)在
x
t
x_t
xt处的梯度(当
x
x
x为一维时,即导数)
∇
f
(
x
t
)
\nabla f(x_t)
∇f(xt);
(2)
x
t
+
1
=
x
t
−
η
∇
f
(
x
t
)
x_{t+1}=x_t-\eta\nabla f(x_t)
xt+1=xt−η∇f(xt)
(3)若
x
t
+
1
x_{t+1}
xt+1与
x
t
x_t
xt相差不大(达到预先设定的范围)或迭代次数达到预设上限,停止算法;否则重复(1)(2).
其中
η
\eta
η为学习率,它决定了梯度下降的步长。
下面是一个用梯度下降法求取
y
=
x
2
y=x^2
y=x2的最小值点的示例程序:
import numpy as np
import matplotlib.pyplot as plt
deff(x):return x **2defdraw():
x = np.linspace(-3,3)
y = f(x)
plt.plot(x, y, c ='red')
cnt =0# 初始化 x
x = np.random.rand(1)*3
learning_rate =0.05whileTrue:
grad =2* x
# -----------作图用,非算法部分-----------
plt.scatter(x, f(x), c ='black')
plt.text(x +0.3, f(x)+0.3,str(cnt))# -------------------------------------
new_x = x - grad * learning_rate
# 判断收敛ifabs(new_x - x)<1e-3:break
x = new_x
cnt +=1
draw()
plt.show()
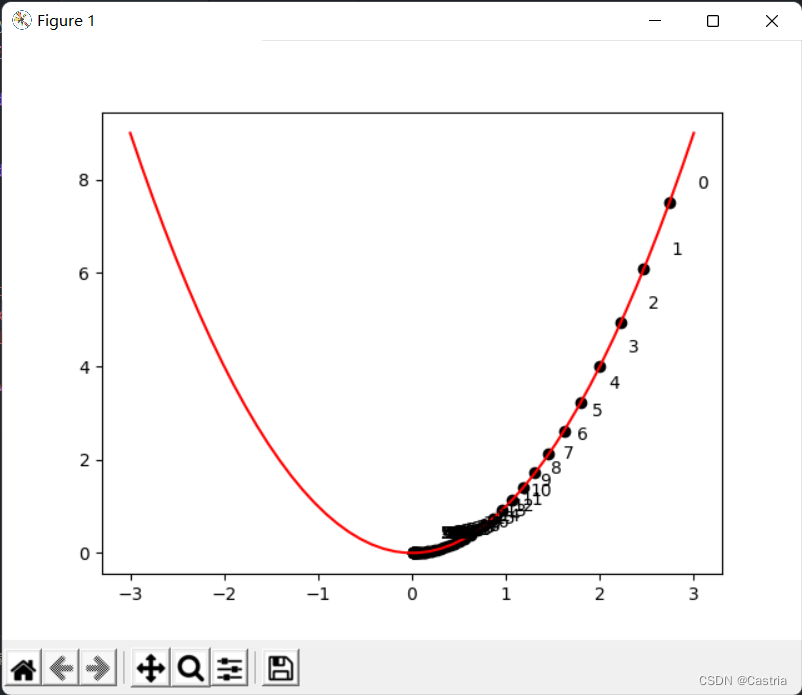
上图标明了
x
x
x随着迭代的演进,可以看到
x
x
x不断沿着正半轴向零点靠近。需要注意的是,学习率不能过大(虽然在上面的程序中,学习率设置得有点小了),需要手动进行尝试调整,否则容易想象,
x
x
x在正负半轴来回震荡,难以收敛。
在最小二乘法中,我们需要优化的函数是损失函数
L
=
(
X
W
−
Y
)
T
(
X
W
−
Y
)
.
L=(XW-Y)^T(XW-Y).
L=(XW−Y)T(XW−Y).
下面我们用梯度下降法求解该问题。在上面的推导中,
∂
L
∂
W
=
2
X
T
X
W
−
2
X
T
Y
,
\begin{aligned}\frac{\partial L}{\partial W}=2X^TXW-2X^TY\end{aligned},
∂W∂L=2XTXW−2XTY,
于是我们每次在迭代中对
W
W
W减去该梯度,直到参数
W
W
W收敛。不过经过实验,平方误差会使得梯度过大,过程无法收敛,因此采用均方误差(MSE)替换之,就是给原来的式子除以
N
N
N:
'''
梯度下降法(Gradient Descent, GD)求优化解, m 为多项式次数, max_iteration 为最大迭代次数, lr 为学习率
注: 此时拟合次数不宜太高(m <= 3), 且数据集的数据范围不能太大(这里设置为(-3, 3)), 否则很难收敛
- dataset 数据集
- m 多项式次数, 默认为 3(太高会溢出, 无法收敛)
- max_iteration 最大迭代次数, 默认为 1000
- lr 梯度下降的学习率, 默认为 0.01
'''defGD(dataset, m =3, max_iteration =1000, lr =0.01):# 初始化参数
w = np.random.rand(m +1)
N =len(dataset)
X = np.array([dataset[:,0]** i for i inrange(len(w))]).T
Y = dataset[:,1]try:for i inrange(max_iteration):
pred_Y = np.dot(X, w)# 均方误差(省略系数2)
grad = np.dot(X.T, pred_Y - Y)/ N
w -= lr * grad
'''
为了能捕获这个溢出的 Warning,需要import warnings并在主程序中加上:
warnings.simplefilter('error')
'''except RuntimeWarning:print('梯度下降法溢出, 无法收敛')return w
这时如果
m
m
m设置得稍微大一点(比如4),在迭代过程中梯度就会溢出,使参数无法收敛。在收敛时,拟合效果还算可以:
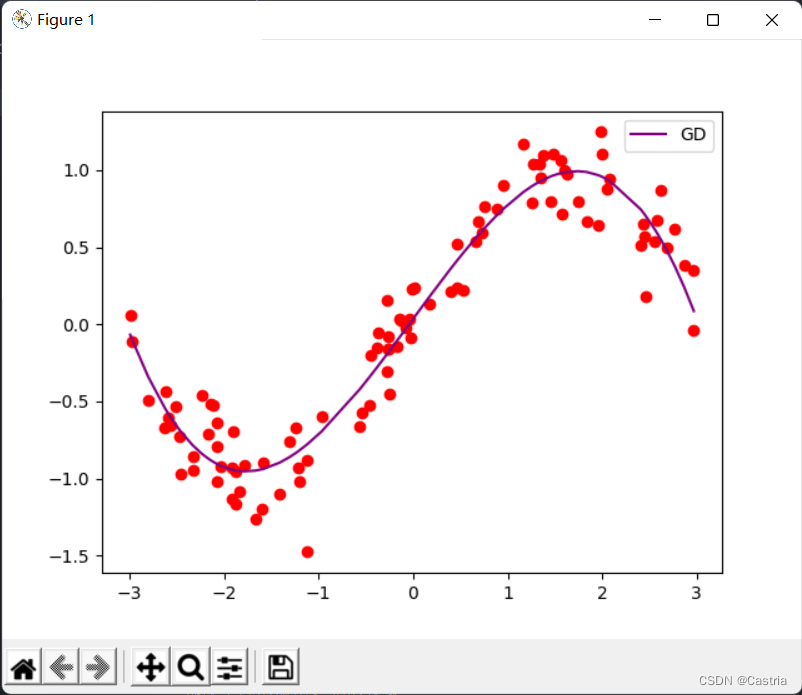
共轭梯度法
共轭梯度法(Conjugate Gradients)可以用来求解形如
A
x
=
b
A\pmb x=\pmb b
Axx=bb的方程组,或最小化二次型
f
(
x
)
=
1
2
x
T
A
x
−
b
T
x
+
c
.
f(\pmb x)=\frac12\pmb x^TA\pmb x-\pmb b^T \pmb x+c.
f(xx)=21xxTAxx−bbTxx+c.(可以证明对于正定的
A
A
A,二者等价)其中
A
A
A为**正定**矩阵。在本问题中,我们要求解
X
T
X
W
=
Y
T
X
,
X^TXW=Y^TX,
XTXW=YTX,
就有
A
(
m
+
1
)
×
(
m
+
1
)
=
X
T
X
,
b
=
Y
T
.
A_{(m+1)\times(m+1)}=X^TX,\pmb b=Y^T.
A(m+1)×(m+1)=XTX,bb=YT.若我们想加一个正则项,就变成求解
(
X
T
X
+
λ
E
)
W
=
Y
T
X
.
(X^TX+\lambda E)W=Y^TX.
(XTX+λE)W=YTX.
首先说明一点:
X
T
X
X^TX
XTX不一定是正定的但一定是半正定的(证明见此)。但是在实验中我们基本不用担心这个问题,因为
X
T
X
X^TX
XTX有极大可能是正定的,我们只在代码中加一个断言(assert),不多关注这个条件。
共轭梯度法的思想来龙去脉和证明过程比较长,可以参考这个系列,这里只给出算法步骤(在上面链接的第三篇开头):
(0)初始化
x
(
0
)
;
x_{(0)};
x(0);
(1)初始化
d
(
0
)
=
r
(
0
)
=
b
−
A
x
(
0
)
;
d_{(0)}=r_{(0)}=b-Ax_{(0)};
d(0)=r(0)=b−Ax(0);
(2)令
α
(
i
)
=
r
(
i
)
T
r
(
i
)
d
(
i
)
T
A
d
(
i
)
;
\alpha_{(i)}=\frac{r_{(i)}^Tr_{(i)}}{d_{(i)}^TAd_{(i)}};
α(i)=d(i)TAd(i)r(i)Tr(i);
(3)迭代
x
(
i
+
1
)
=
x
(
i
)
+
α
(
i
)
d
(
i
)
;
x_{(i+1)}=x_{(i)}+\alpha_{(i)}d_{(i)};
x(i+1)=x(i)+α(i)d(i);
(4)令
r
(
i
+
1
)
=
r
(
i
)
−
α
(
i
)
A
d
(
i
)
;
r_{(i+1)}=r_{(i)}-\alpha_{(i)}Ad_{(i)};
r(i+1)=r(i)−α(i)Ad(i);
(5)令
β
(
i
+
1
)
=
r
(
i
+
1
)
T
r
(
i
+
1
)
r
(
i
)
T
r
(
i
)
,
d
(
i
+
1
)
=
r
(
i
+
1
)
+
β
(
i
+
1
)
d
(
i
)
.
\beta_{(i+1)}=\frac{r_{(i+1)}^Tr_{(i+1)}}{r_{(i)}^Tr_{(i)}},d_{(i+1)}=r_{(i+1)}+\beta_{(i+1)}d_{(i)}.
β(i+1)=r(i)Tr(i)r(i+1)Tr(i+1),d(i+1)=r(i+1)+β(i+1)d(i).
(6)当
∣
∣
r
(
i
)
∣
∣
∣
∣
r
(
0
)
∣
∣
<
ϵ
\frac{||r_{(i)}||}{||r_{(0)}||}<\epsilon
∣∣r(0)∣∣∣∣r(i)∣∣<ϵ时,停止算法;否则继续从(2)开始迭代。
ϵ
\epsilon
ϵ为预先设定好的很小的值,我这里取的是
1
0
−
5
.
10^{-5}.
10−5.
下面我们按照这个过程实现代码:
'''
共轭梯度法(Conjugate Gradients, CG)求优化解, m 为多项式次数
- dataset 数据集
- m 多项式次数, 默认为 5
- regularize 正则化参数, 若为 0 则不进行正则化
'''defCG(dataset, m =5, regularize =0):
X = np.array([dataset[:,0]** i for i inrange(m +1)]).T
A = np.dot(X.T, X)+ regularize * np.eye(m +1)assert np.all(np.linalg.eigvals(A)>0),'矩阵不满足正定!'
b = np.dot(X.T, dataset[:,1])
w = np.random.rand(m +1)
epsilon =1e-5# 初始化参数
d = r = b - np.dot(A, w)
r0 = r
whileTrue:
alpha = np.dot(r.T, r)/ np.dot(np.dot(d, A), d)
w += alpha * d
new_r = r - alpha * np.dot(A, d)
beta = np.dot(new_r.T, new_r)/ np.dot(r.T, r)
d = beta * d + new_r
r = new_r
# 基本收敛,停止迭代if np.linalg.norm(r)/ np.linalg.norm(r0)< epsilon:breakreturn w
相比于朴素的梯度下降法,共轭梯度法收敛迅速且稳定。不过在多项式次数增加时拟合效果会变差:在
m
=
7
m=7
m=7时,其与最小二乘法对比如下:
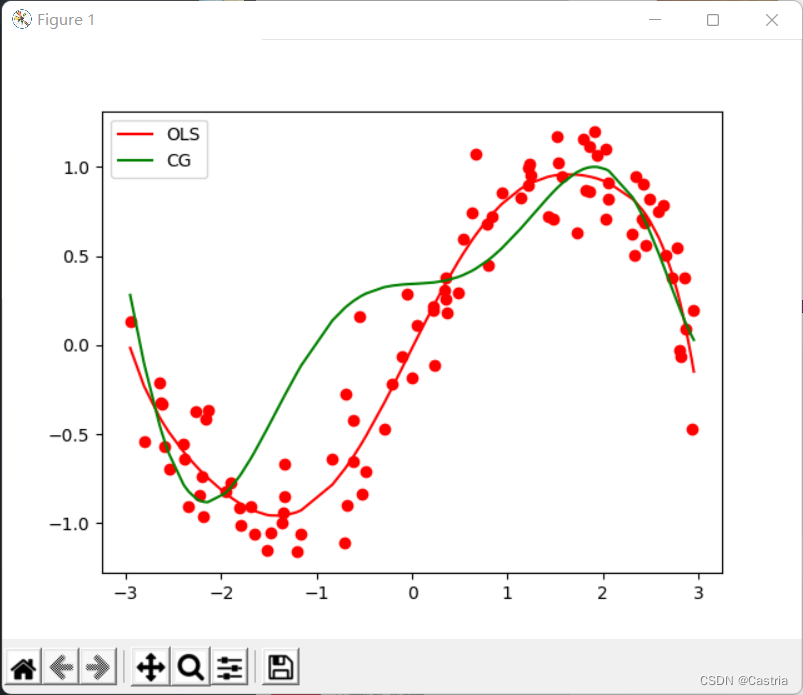
此时,仍然可以通过正则项部分缓解(图为
m
=
7
,
λ
=
1
m=7,\lambda=1
m=7,λ=1):
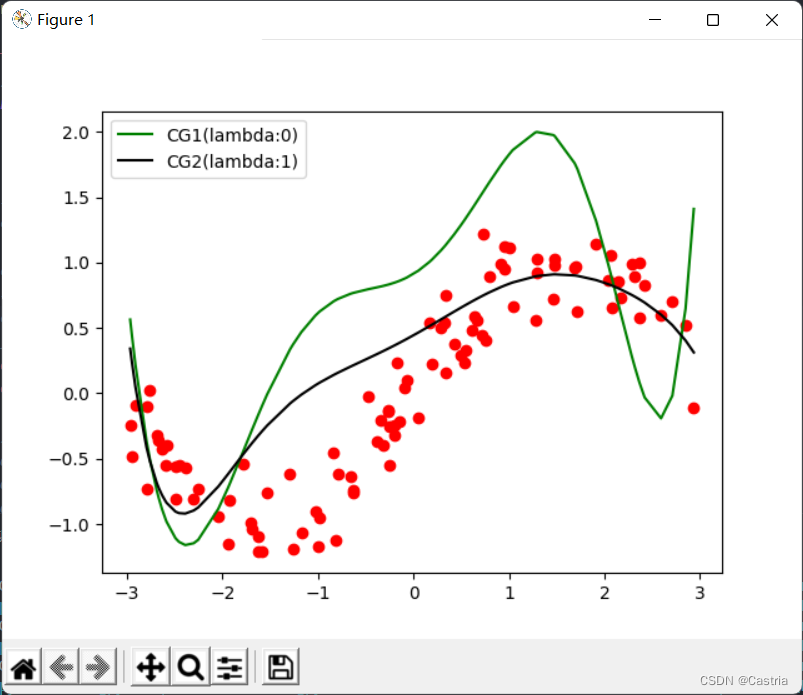
最后附上四种方法的拟合图像(基本都一样)和主函数,可以根据实验要求调整参数: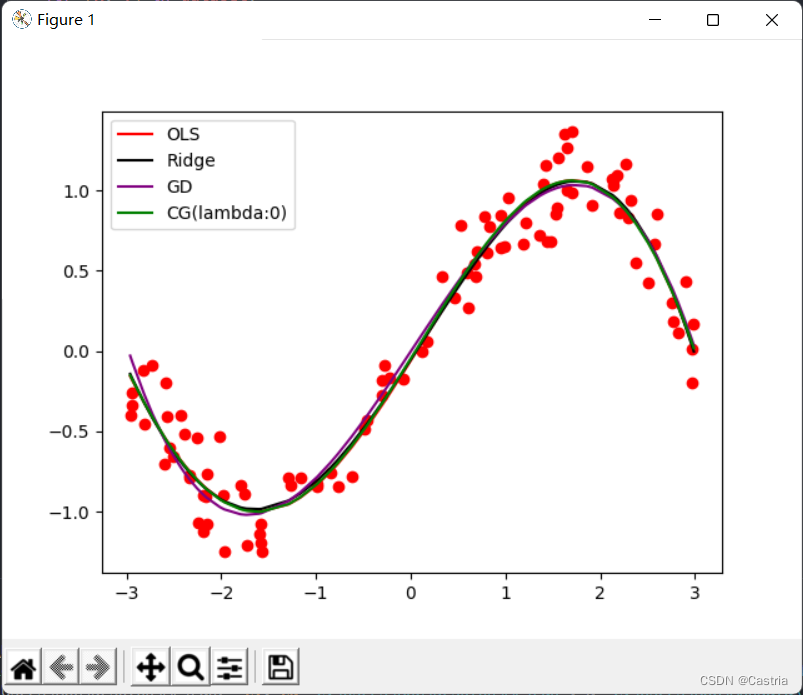
if __name__ =='__main__':
warnings.simplefilter('error')
dataset = get_dataset(bound =(-3,3))# 绘制数据集散点图for[x, y]in dataset:
plt.scatter(x, y, color ='red')# 最小二乘法
coef1 = fit(dataset)# 岭回归
coef2 = ridge_regression(dataset)# 梯度下降法
coef3 = GD(dataset, m =3)# 共轭梯度法
coef4 = CG(dataset)# 绘制出四种方法的曲线
draw(dataset, coef1, color ='red', label ='OLS')
draw(dataset, coef2, color ='black', label ='Ridge')
draw(dataset, coef3, color ='purple', label ='GD')
draw(dataset, coef4, color ='green', label ='CG(lambda:0)')# 绘制标签, 显示图像
plt.legend()
plt.show()
版权归原作者 Castria 所有, 如有侵权,请联系我们删除。