【Java数据结构】二叉树丶二叉树进阶——大厂经典OJ面试题

【Java数据结构】二叉树丶二叉树进阶——大厂经典OJ面试题

由于博主是在学小白一枚，难免会有错误，有任何问题欢迎评论区留言指出，感激不尽！~

文章目录

判断两颗数是否相同

题目：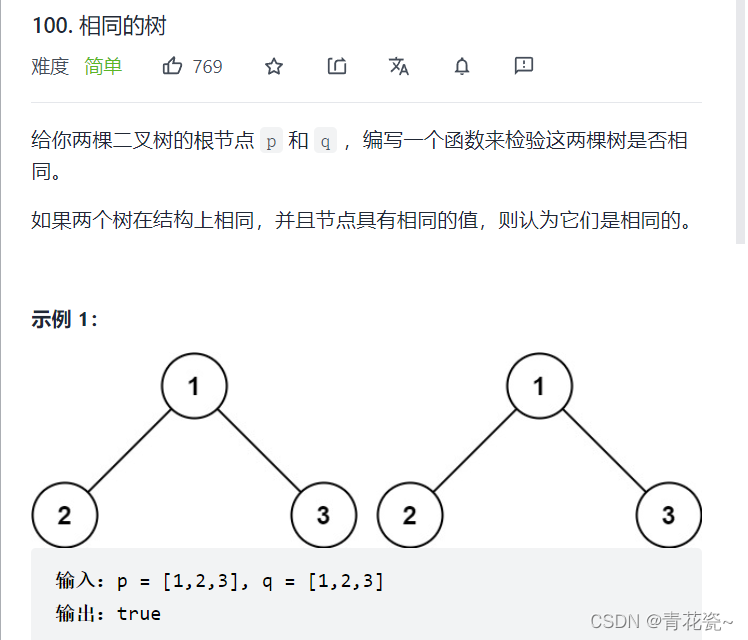

思路：

1.首先要明确两棵树相同，指的是左子树和右子树结构相同，且值也相同
2.先判断，两棵树的根节点是否为空，如果两棵树的根节点都是空，那这两棵树相同，直接返回true
3.如果两棵树只有一棵树的根节点为空，另一棵树的根节点不为空，那这两棵树必不相同，直接返回false
4.如果两棵树的根节点都不为空，那就比较他们的值，如果值不一样，两棵树就不相同，返回false
5.当以上条件都没返回false，说明两棵树的根节点都相同，那么就用递归的方法去判断他们的左右孩子节点是否相同

代码实现：

   class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //第一种情况 p和q一个不等于空
        if(p == null && q != null || p != null && q == null) {
            return false;
        }
        //第二种情况 p和q都等于空
        if(p == null && q == null) {
            return true;
        }
        //第三种情况 p和p不等于空 但是 p和q 的值不相同
        if(p.val != q.val) {
            return false;
        }
        //最后 p != null && q != null && p.val== q.val
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
       }
}

另一棵树的子树

题目：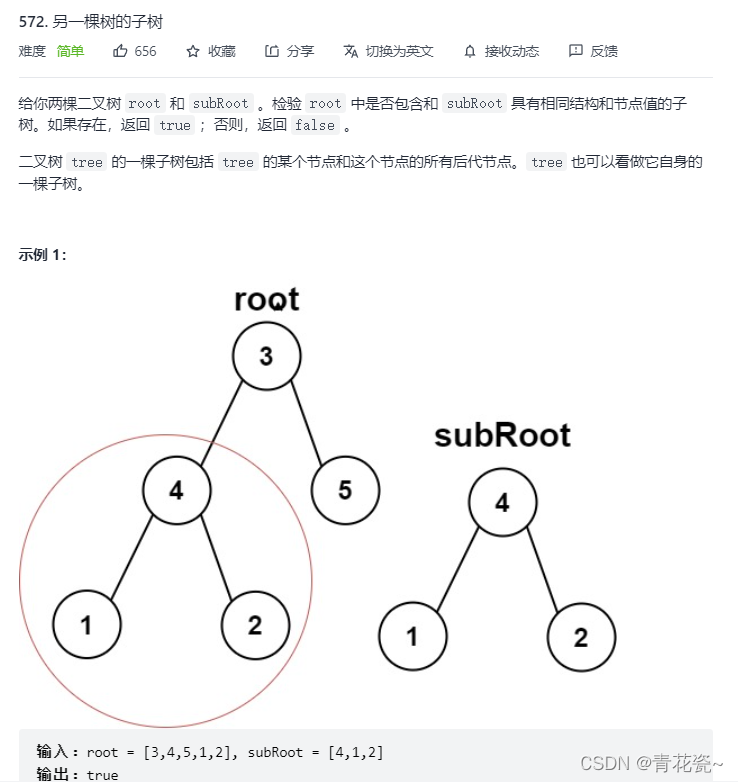

思路：
1.先判断两颗树是不是相同的 数(参考上题，代码一模一样)
2.如果不是，那么分别判断subRoot是root的左子树还是右子树

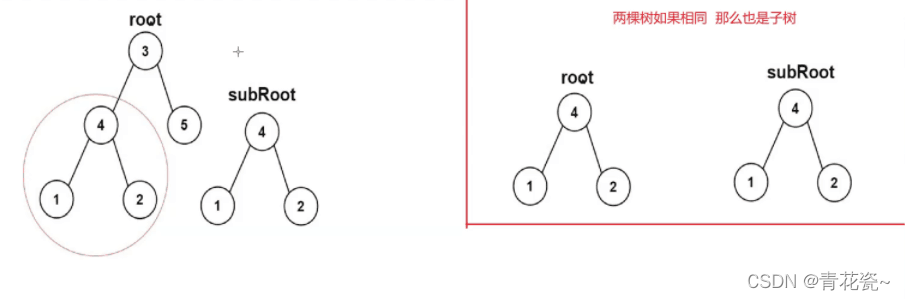
代码实现：

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //第一种情况 p和q一个不等于空
        if(p == null && q != null || p != null && q == null) {
            return false;
        }
        //第二种情况 p和q都等于空
        if(p == null && q == null) {
            return true;
        }
        //第三种情况 p和p不等于空 但是 p和q 的值不相同
        if(p.val != q.val) {
            return false;
        }
        //最后 p != null && q != null && p.val== q.val
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        //如果有一个为空 返回false
        if(root == null || subRoot == null) {
            return false;
        }
        //先判断根节点和subRoot是不是相同的数
        if(isSameTree(root,subRoot)) {
            return true;
        }
        //subRoot是不是root的左子树或
        if(isSubtree(root.left,subRoot)) {
            return true;
        }
        //subRoot是不是root的右子树
        if(isSubtree(root.right,subRoot)) {
            return true;
        }
        //都不是返回flase
        return false;
    }
}

求二叉树的最大深度

题目：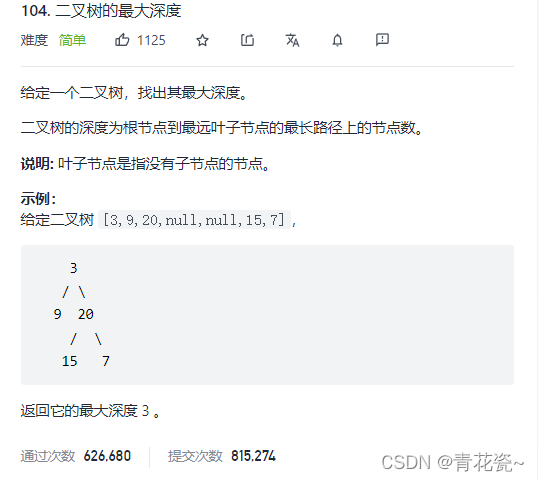

思路：
1.利用 子问题思路 来解决：左右子树取最大深度 然后+1（根节点）
2.理解深度是什么：二叉树的高度
3.递归方法

代码实现：

class Solution {
    public int maxDepth(TreeNode root) {
      if(root == null) {
          return 0;//如果根节点为0返回0
      }
      //下一步根节点不为0 我们用递归的方法分别取找 左子树和右子树的高度
      int leftHeight = maxDepth(root.left);
      int rightHeight = maxDepth(root.right);
      //这里使用三目运算符 如果左子树的高度大于右子树那么就让左子树加1（加上根节点）
      return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
   }
}

判断一颗二叉树是否是平衡二叉树

题目：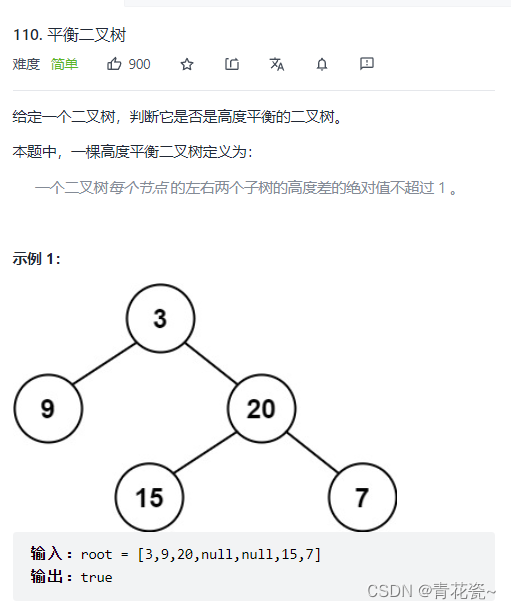

思路：
1.首先，我们需要知道 平衡二叉树的定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
2.采取从下往上看的思路，额外写一个判断树高度的方法
3.判断当前根节点的左子树高度和右子树高度之差的绝对值是否不超过1
4.符合平衡条件则返回子树高度，否则返回

代码实现：

class Solution {//时间复杂度O（n）
    int getHeight(TreeNode root) {
      if(root == null) {
          return 0;
      }
      int HeightLeft = getHeight(root.left);
      int HeightRight = getHeight(root.right);
      if(HeightLeft>=0 && HeightRight>=0 && Math.abs(HeightLeft - HeightRight) <=1) {
          return Math.max(HeightLeft,HeightRight) + 1;
      }else{
          return -1;
      }
    }
    public boolean isBalanced(TreeNode root) {
         if(root == null) return true;
         return getHeight(root) >= 0;
    }
}

对称二叉树

题目：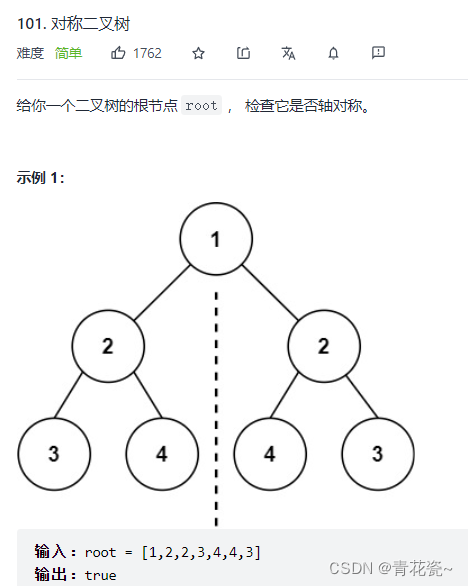

思路：
1.判断

root的左右子树是否对称

2.判断:

左子树左孩子的值和右子树右孩子的值是否相同

左子树右孩子的值和右子树左孩子的值是否相同

代码实现：

class Solution {
    public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree) {
        if(leftTree == null && rightTree != null) return false;
        if(leftTree != null && rightTree == null) return false;
        if(leftTree == null && rightTree == null) return true;
        if(leftTree.val != rightTree.val) return false;
        return isSymmetricChild(leftTree.left,rightTree.right) &&
                isSymmetricChild(leftTree.right,rightTree.left);
    }
    public boolean isSymmetric(TreeNode root) {
          if(root == null) return true;
        return isSymmetricChild(root.left,root.right);
    }
}

大厂OJ面试题

二叉树的创建及遍历

题目：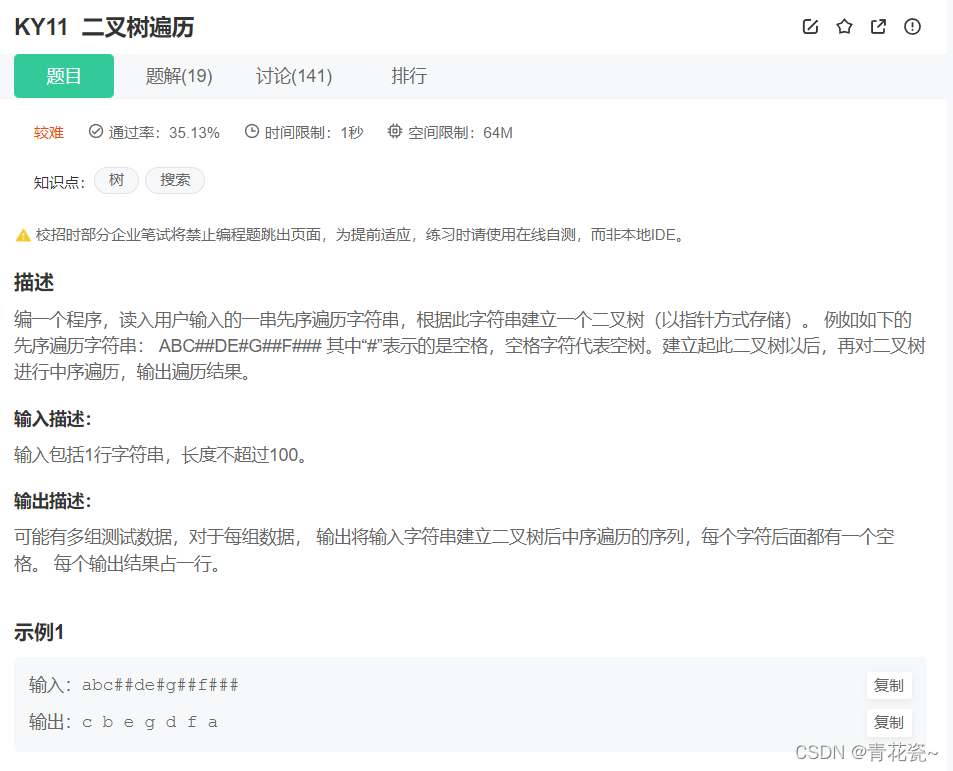

思路：
1.根据题意的输出结果我们可以知道，这是通过 前序遍历 构建的二叉树，因此我们去遍历这些字符串
2.构建二叉树我们也要根据前序遍历来构建，也就是根->左->右

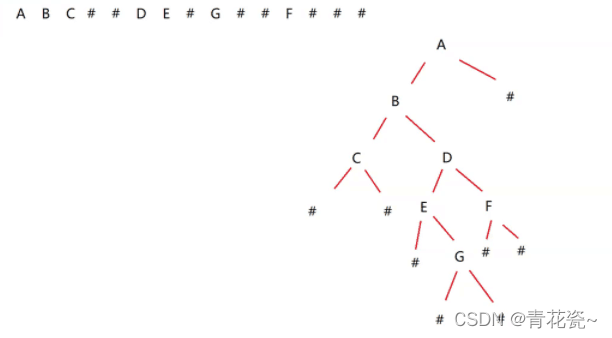
代码实现：

   
import java.util.*;
//定义一个节点
class TreeNode{
    char value;//节点的值
    TreeNode left;//左孩子节点
    TreeNode right;//右孩子节点
    public TreeNode(char value){//构造函数
        this.value = value;
    }
}

public class Main{
 //主函数，用于输入字符串，主要在creatTree方法里来实现
 public static void main(String[]args){
        Scanner scanner = new Scanner(System.in);
        String str = scanner.nextLine();
        TreeNode root =  creatTree(str);
        inOrderTraveled(root);
    }

  
    public static int i = 0;//i用于记录字符串中字符的下标
    //因为构建过程是递归的，不能用局部变量，所以要在外部设置成静态的
    public static TreeNode creatTree(String str){
        if(str==null){//如果字符串为空
            return null;//直接返回null
        }
        //字符串不为空，就进行构构建二叉树的过程
        TreeNode root = null;//先创建一个根节点，指向空，这样做是为了初始化
        if(str.charAt(i)!='#'){//依次读取字符串中的字符，不为 # 就进行二叉树构造
            root = new TreeNode(str.charAt(i));//将读取的字符给节点实例化
            i++;//当前读取的字符被用过之后，字符串下标要往后走一位
            root.left = creatTree(str);//递归构建左树
            root.right = creatTree(str);//递归构建右树
        }else{//读取到的字符是 # ，代表空节点，不用构建
            i++;//字符串下标往后走一位
        }
        return root;//最后返回根节点即可
    }
    
    //对构建好的二叉树进行中序遍历，用递归实现就好了
    public static void inOrderTraveled(TreeNode root){
        if(root==null) return;
        inOrderTraveled(root.left);
        System.out.print(root.value+" ");
        inOrderTraveled(root.right);
    }

二叉树的分层遍历进阶（返回二维数组）

题目：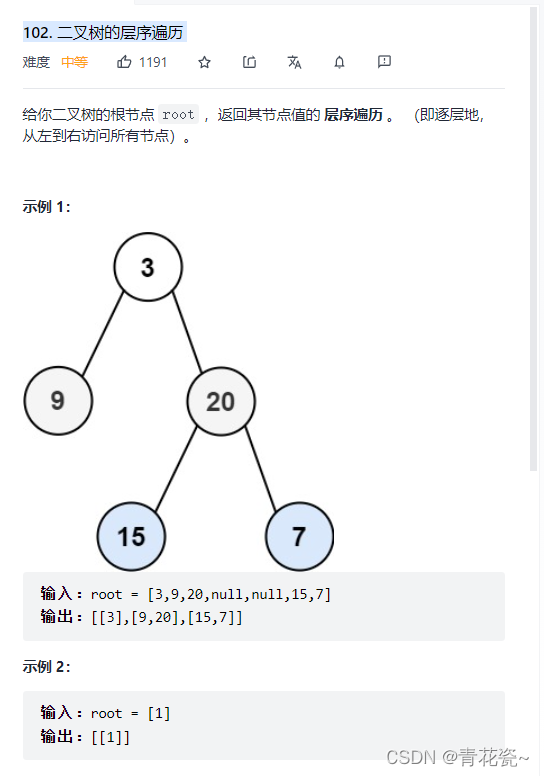

思路：
1.层序遍历就是 从左往右 一层一层的遍历节点
2.这题还有一个要求就是，输出的时候将一层的节点放在一行，下一层的节点放在下一行，这就需要用到

一个二维数组来储存每一层的节点

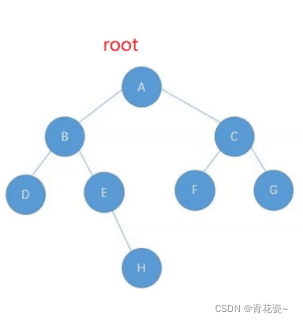
第一层放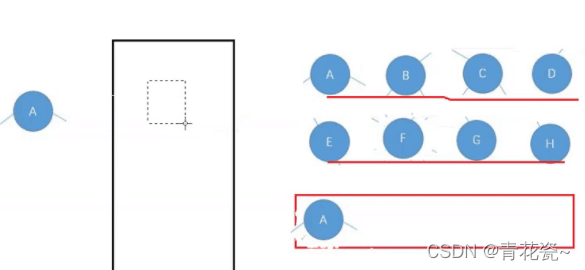

第二层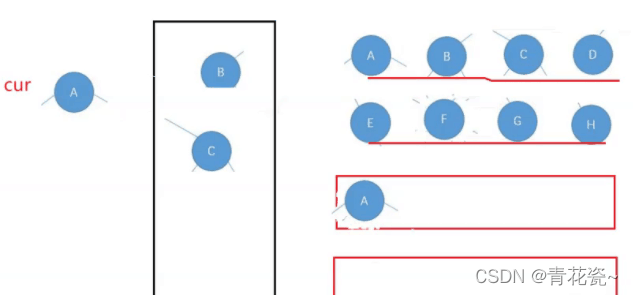

如此循环

代码实现：

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<>();//二维数组
        if(root == null) {
            return ret;//如果root等于空 返回二维数组
        }
        Queue<TreeNode> queue = new LinkedList<>();//new一个队列来存放元素
        queue.offer(root);//root不等于空 入队列
        while (!queue.isEmpty()) {
            int size =queue.size();//这个值代表当前层有多少个节点
            List<Integer> list = new ArrayList<>();//new一个列表来存放弹出的元素，这样就可以分层了
            while (size != 0) {
                TreeNode cur = queue.poll();
                //弹出的元素放入二维数组当中
                list.add(cur.val);
                if(cur.left != null){
                    queue.offer(cur.left);
                }
                if(cur.right != null) {
                    queue.offer(cur.right);
                }
                size--;
            }
            ret.add(list);//将list里面的元素放入 二维数组
        }
        return ret;//返回二维数据
    }
}

二叉树的层序遍历

思路：用队列，先将二叉树数的一个节点放入队列中，判断队列为不为空，如果不为空弹出队顶元素，如果弹出元素的左节点不为空，放入，弹出节点右节点不为空，放入。思路很简单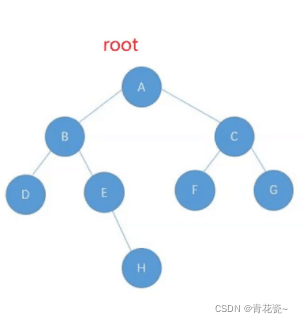

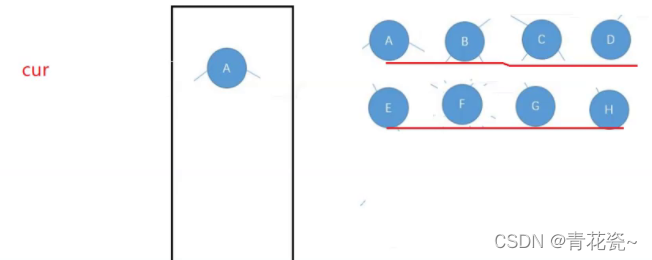
代码实现：

public void levelOrder1(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        if(root == null) {
            return;
        }
        //root不为空，放入队列
        queue.offer(root);
        //判断队列为不为空
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.val+" ");
            //cur的左不等于空 cur的左入队列
            if(cur.left != null){
                queue.offer(cur.left);
            }
            //cur的右补位空 cur的右入队列
            if(cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

二叉树的最近公共祖先（LCA问题）两种思路教你解决

题目：

做这道题之前我们需要明白什么叫做 公共祖先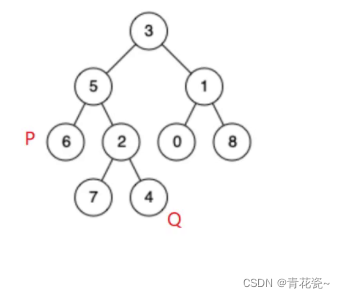

比如 p为6 q为4 那么 p和q的 公共祖先 就是5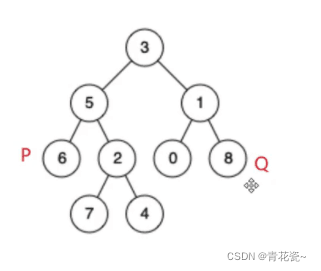

p和q的 公共祖先 为 3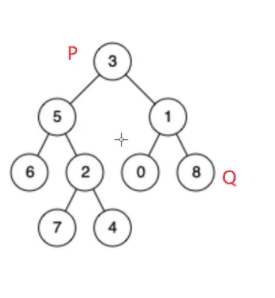

p和q的 公共祖先 为 p 本身 3

思路：
如果给定的树是二叉搜索树
这里扩展一下 什么是 二叉搜索树
简单的说明一下它的特点：
1.

中序遍历是有序的

1. 根节点的左树 都比根小 根节点的右树 都比根大
   

（前面我写过一篇二叉搜索树的基本操作的博客，如果想要学习，可以去看看哟）

思路一：
1.第一种情况

root==p || root ==q

此时最近公共祖先 是 root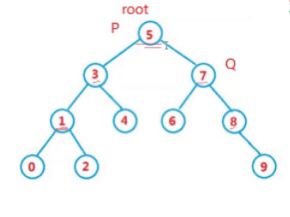

2.第二种情况

p.val < root.val && q.val < root.va

l p和q 都在root的 左子树当中

最近公共祖先 在root的 左树当中

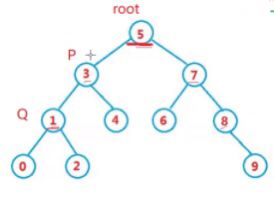
3.同理

p.val > root && q.val > roo

t p和q 都在 root 的右子树当中

最近公共祖先在root的右树当中

1. p.val > root.val && q.val < root.val
   

   说明 p和q 分别在 roo t的左子树 和右子树当中 此时

   最近公共祖先就是root
   

代码实现:

class Solution {
 public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
     //根节点
     if(root == null) {
         return null;
     }
     if(root == p || root == q) {
         return root;
     }
     //开始递归
     TreeNode left = lowestCommonAncestor(root.left,p,q);
     TreeNode right = lowestCommonAncestor(root.right,p,q);
     //p和q分别在左右两子树的情况
     if(right != null && left != null) {
         return root;
     }
     //pq在左树的情况(返回左树找到的元素)
     if(left != null && right ==null) {
         return left;
     }
     if(left == null && right != null) {
         return right;
     }
     return null;
 }
}

思路二：

链表求交点

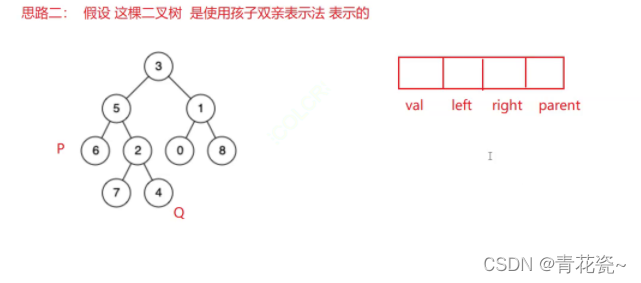
首先 判断 p 和 q 到 root 各自分别要走多少步，

再让 步数多的 走 差值步，最后一起走，相遇的节点就是 我们所求的 公共祖先

这种思路比较可惜的是：我们的二叉树 每个节点 是没有双亲 节点的。

所有我们 这道题 用

栈

来做，用

栈来存储 根到 节点的路径

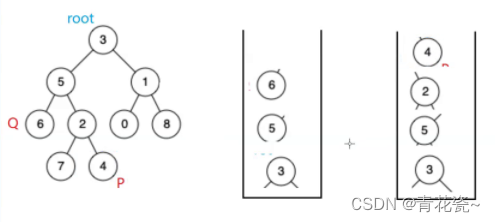
1.

用两个栈来存储路径

1. 求栈的大小
   

2. 让栈中 多的元素 出差值个元素
   

3. 开始出栈，直到栈顶元素相同
   

   此时就是公共祖先
   

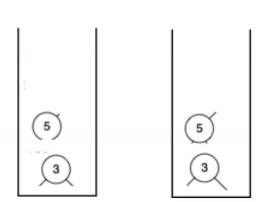
代码实现：

class Solution {
    //找根节点到指定节点的路径 放入栈中
    //root代表根节点  node代表指定节点  stack代表存放从根节点到指定节点的路径
    public boolean getPath(TreeNode root,TreeNode node,Stack<TreeNode> stack) {
        if(root == null || node == null) return false;
        //如果不为空，先把root节点 入栈
        stack.push(root);
        if(root == node) return true;//如果root等于node说明找到了
        //如果root不等于 node 分别从 root的左边和右边开始找
        boolean flg = getPath(root.left,node,stack);
        if(flg == true) {
            return true;
        }
        flg = getPath(root.right,node,stack);
            if(flg == true) {
                return true;
            }
            //如果root的左右都没有找到
            stack.pop();//弹出
            return false; 
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) return null;
        //第一个栈
        Stack<TreeNode> stack1 = new Stack<>();
        //把根到p的路径放入stack1中
        getPath(root,p,stack1);
        Stack<TreeNode> stack2 = new Stack<>();
        //把根到q的路径让如stack2中
        getPath(root,q,stack2);
        int size1 = stack1.size();
        int size2 = stack2.size();
        //判断大小
        if(size1 > size2) {
            int size = size1 - size2;
            while(size != 0) {
                //出第一个栈里的元素
                stack1.pop();
                size--;
            }
            while(!stack1.isEmpty() && !stack2.isEmpty()) {
                if(stack1.peek() == stack2.peek()) {
                    return stack1.pop();
                }else{
                    stack1.pop();
                    stack2.pop();
                }
            }
        }else{
            int size = size2 - size1;
            while(size != 0) {
                //出第一个栈里的元素
                stack2.pop();
                size--;
            }
            while(!stack1.isEmpty() && !stack2.isEmpty()) {
                if(stack1.peek() == stack2.peek()) {
                    return stack1.pop();
                }else{
                    stack1.pop();
                    stack2.pop();
                }
            }
        }
        return null;
    }
}

二叉搜索树与双向链表

题目：

思路：
将这幅图转变为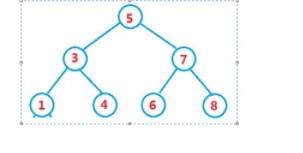

这幅图

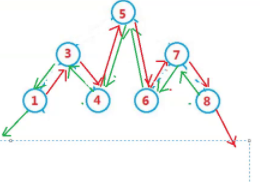
需要在中序遍历过程中，修改每个节点的left和right

做法核心
1.中序遍历 保证有序
2.如何修改指向 形成 双向 链表

代码实现：

TreeNode prev = null;

    public void inorder(TreeNode pCur) {
        if(pCur == null) return;
        inorder(pCur.left);

        //打印
        pCur.left = prev;
        if(prev != null) {
            prev.right = pCur;
        }
        prev = pCur;
        //System.out.print(pCur.val+" ");
        inorder(pCur.right);
    }

    public TreeNode Convert(TreeNode pRootOfTree) {

        if(pRootOfTree == null) return null;

        inorder(pRootOfTree);

        TreeNode head = pRootOfTree;
        while(head.left != null) {
            head = head.left;
        }
        return head;
    }

根据一棵树的前序遍历与中序遍历构造二叉树

题目: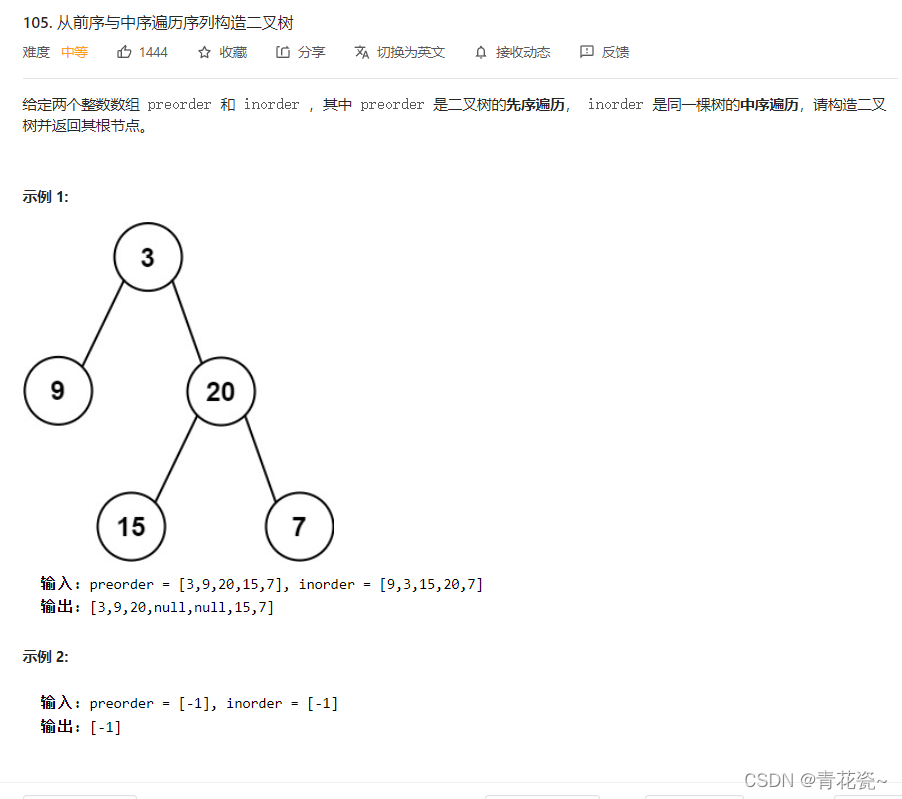

举个简单的例子：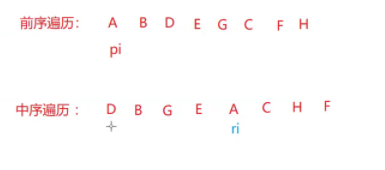

我们可以看出 根的左树 应该是 ri 左边那部分 根的右树应该是 ri 右边的部分

思路：
1.

先将 pi 下标的元素 创建为root

1. 在中序遍历的数组当中，找到当前 pi 下标的元素，存在的位置
   

2. root的左树等于谁，root的右树等于谁
   

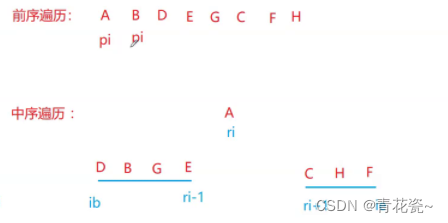
代码实现：

class Solution {
    public int preIndex = 0;
    public TreeNode createTreeByPandI(int[] preorder, int[] inorder,int inbegin,int inend) {
        if(inbegin > inend) {
            //如果满足这个条件  说明 没有左树 或者 右树了
            return null;
        }
        TreeNode root = new TreeNode(preorder[preIndex]);
        //找到根在中序遍历的位置
        int rootIndex = findIndexOfI(inorder,inbegin,inend,preorder[preIndex]);
        if(rootIndex == -1) {//如果没找到
            return null;
        }
        preIndex++;
        //分别创建 左子树 和 右子树
        root.left = createTreeByPandI(preorder,inorder,inbegin,rootIndex-1);
        root.right = createTreeByPandI(preorder,inorder,rootIndex+1,inend);
        return root;
    }
    //找元素
    private int findIndexOfI(int[] inorder,int inbegin,int inend,int key) {

        for(int i = inbegin; i <= inend;i++) {
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder == null || inorder == null) return null;
        return createTreeByPandI(preorder,inorder,0,inorder.length-1);
    }
}

二叉树创建字符串

题目：

思路：
1.

如果当前节点有两个孩子，那我们在递归时，需要在两个孩子的结果外都加上一层括号

；
2.

如果当前节点没有孩子，那我们不需要在节点后面加上任何括号

；
3.

如果当前节点只有左孩子，那我们在递归时，只需要在左孩子的结果外加上一层括号，而不需要给右孩子加上任何括号

；
4.

如果当前节点只有右孩子，那我们在递归时，需要先加上一层空的括号 () 表示左孩子为空，再对右孩子进行递归，并在结果外加上一层括号

。

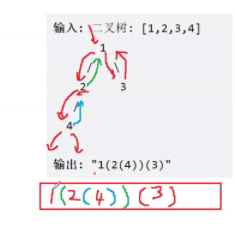
代码实现：

class Solution {
    public void tree2strChild(TreeNode root,StringBuilder sb) {
        if(root == null) return ;
        sb.append(root.val);//前序遍历，先将根节点加入可变字符串
        
        if(root.left==null){//左树为空，还得考虑右树的情况
            if(root.right==null){//如果右树为空，说明当前根节点没有孩子
            //直接返回，因为题目要求把不必要的（）省略
                return;
            }else{//右树不为空，加（），这里还在左树，这个（）是表示左子树为空
            //因为右树不为空，所有不能省略
                sb.append("()");
            }
        }else{//左树不为空，先加（，然后继续遍历左树，再加）
            sb.append("(");
            tree2strChild(root.left,sb);
            sb.append(")");
        }

        //左树遍历完要遍历右树了
        if(root.right==null){//如果右树为空
            return;//直接返回，因为省略（）不会影响字符串与树的映射关系
        }else{//否则，先加（，然后继续遍历右树，再加）
            sb.append("(");
            tree2strChild(root.right,sb);
            sb.append(")");
        }
    }
    public String tree2str(TreeNode root) {
        if(root==null) return null;
        StringBuilder sb = new StringBuilder();
        tree2strChild(root,sb);
        return sb.toString();
    }
}

萌新写博客，若有地方没有总结好的，希望大佬们多多提出哈~~

0.0